基于改进LSSVM的短时交通流量预测

娄婉秋

（四川大学计算机学院，成都 610065）

基于改进LSSVM的短时交通流量预测

娄婉秋

（四川大学计算机学院，成都 610065）

为提高短时交通流量预测的准确性，提出一种基于改进LSSVM的短时交通流量预测模型。针对传统混合蛙跳算法（SFLA）容易陷入局部最优的问题，提出基于新局部更新策略的改进混合蛙跳算法（ISFLA）,在此基础上将其与最小二乘支持向量机（LSSVM）相结合，通过采用该算法优化LSSVM的关键参数，从而提高LSSVM的预测能力。结合实例，对模型和算法进行仿真分析，证明模型的可行性和算法的有效性。

短时交通流量预测；最小二乘支持向量机；改进蛙跳算法；参数选择；智能优化算法

0 引言

排序是计算机程序设计中一项基本的操作，在实际应用中，有很多情况下需要对数据按照某种方式进行排序后才能达到某种要求，因此，学习和研究各种排序方法是计算机工作者的重要课题之一。

对交通流量进行精确的预测是缓解交通堵塞现象的重要基础，也是实现智能交通系统的一个核心部分。交通流量预测是指基于当前和过去的交通流量信息，使用合适的预测模型对未来的交通流量进行预测。其中短时交通流量预测是指时间范围在30分钟内的预测。由于短时交通流量具有随机性、不确定性和突发性，对短时交通流量进行有效准确预测是智能交通管理领域的一个难题。

针对短时交通流量预测，国内外学者提出了许多预测方法。一类是传统的数学方法，例如卡尔曼滤波方法[1]、自回归滑动平均方法[2]。这些方法实现简单，对于缓慢变化的交通流量预测效果较佳；缺点则是无法反映交通流中的不确定性和非线性，难以对短时交通流量进行精确预测。针对这个问题，学者们提出了另外一类基于人工智能的方法，例如神经网络方法[3]和支持向量机方法[4]。神经网络模型虽然在描述非线性系统中有杰出的性能，但是过于强调学习误差，这会导致过拟合，并且，由于神经网络方法基于经验风险最小化原则，导致在处理小样本数据时效果不佳。而支持向量机克服了神经网络模型的上述固有缺点[5]，其中，最小二乘支持向量机（LSSVM），对标准支持向量机进行了改进，广泛应用于短时交通流量预测中[6]。该算法的预测结果与其相关参数的选取密切相关。不合适的参数选择会导致LSSVM预测能力下降。目前已经采用遗传算法、粒子群算法、网格搜索算法[7～8]等对LSSVM的相关参数进行优化。然而这些算法有容易陷入局部最优值，初始参数设置过多等缺点。

混合蛙跳算法（Shuffled Frog Leaping Algorithm, SFLA）是2003年Muzaffar Eusuff和Kevin Lansey提出的一种新型群体智能优化算法，可以用于解决许多复杂的如非线性、多维的优化问题[9]。该算法结合了粒子群算法（PSO）和模因算法（MA）的优点，并且具有容易理解、设置参数少、计算速度快以及全局搜索寻优能力较佳的特点。

跟大多数智能优化算法一样，SFLA算法也易陷入局部最优值。针对这个问题，本文首先对SFLA算法进行了改进，通过提出新的局部个体更新策略在一定程度上使算法跳出局部最优，获得更优的优化结果。在此基础上，提出改进混合蛙跳算法优化最小二乘支持向量机的短时交通流量预测模型（ISFLA-LSSVM），通过优化LSSVM中影响其预测能力的正则化参数γ和核参数σ，以提高短时交通流量的预测精度。并通过仿真实验验证了ISFLA-LSSVM的有效性。

1 方法介绍

对于给定的训练数据样本集，D=｛（x1，y1），…，（xk，yk），…，（xn，yn）｝，xk∈R，yk∈R，其中xi是时间序列样本的输入，yi是相应的输出，n是训练样本数目。通过非线性函数Ø（x），LSSVM方法把样本空间映射到高维特征空间中进行回归，回归函数如下所示：

其中w是权重，b是偏差值，f（x）表示预测值。根据结构风险最小化原则，LSSVM的回归问题可以表示为如下所示的优化问题：

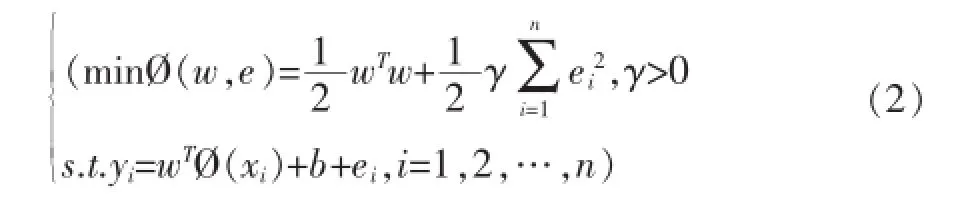
其中ei是误差变量，表示实际值与预测值之间的误差，γ是正则化参数，用于平衡模型的训练误差和复杂度。为了解决上述优化问题，建立拉格朗日函数：

其中αi表示拉格朗日算子。分别对w、b、e、α求偏微分并设置为零，有：

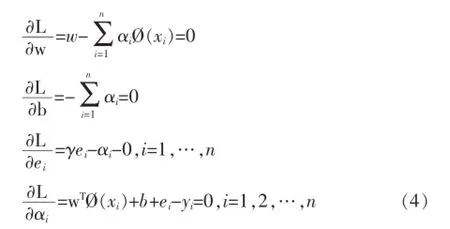
从上述方程组中消去w和e后，可以得到：

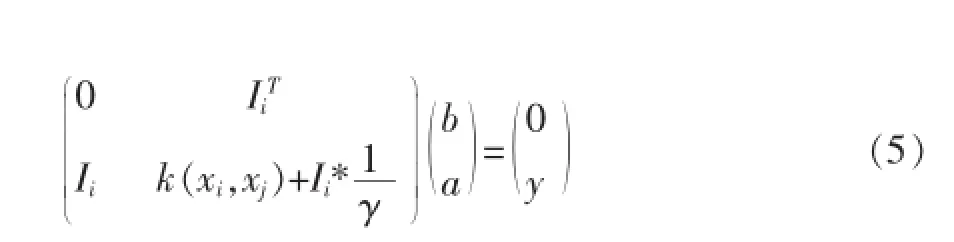
式中y=［y1；…yi；…yn］，Ii=［1；…1］，α=［α1；…；αn］，k（xi，xj）=Ø（xi）Ø（xj）T，所求的拟合函数为：

本文中采用的核函数为径向基函数，k（xi，xj）=exp（-‖xi-xj‖2/δ2），其中σ表示核函数的宽度。选定核函数后，需要选择合适的正则化参数γ和核参数σ。这两个参数会影响LSSVM的学习能力和泛化性能。本研究采用改进蛙跳算法对上述两个参数进行优化，以提高短时交通流量的预测精度。

2 ISFLA-LSSVM的交通流量预测

2.1 传统SFLA算法

SFLA算法是模仿青蛙群体寻找食物的过程而提出的一种新型智能优化算法。该算法包括两个核心过程：青蛙子群间的全局信息交换过程以及子群内部的局部更新过程[10]。

（1）子群间全局信息交换

①参数初始化：随机产生L只青蛙组成初始青蛙群体G={X1，X2，…，XL}，每一只青蛙个体X表示所求问题的一个可行解，即如下所示：X=（x1，x2，…，xd），其中d表示青蛙个体的维数。

②计算种群中所有青蛙个体X的适应度值f（X）并按适应度值大小进行降序排序。将排序后的整个青蛙群体分为m个子群，每个子群有n只青蛙，其中m和n满足L=m×n。分群规则如下所示：第一只青蛙属于第一个子群，第二只青蛙属于第二个子群，依次分配直到第n只青蛙属于第n个子群，然后循环使第n+1只青蛙又属于第一个子群，直到所有的青蛙都分配完毕。对于青蛙群体，我们用Gb表示全局具有最大适应度值的解。对于每一个子群，我们分别用Zb和Zw表示具有最大适应度值和最小适应度值的解。

③子群内部局部迭代搜索：根据②中的搜索过程对每一个子群中拥有最小适应度值的青蛙个体位置进行更新。

④将每个子群中的所有青蛙个体全部混合为一个新群体并按适应度值大小重新进行降序排序。

⑤算法结束条件判断：判断迭代次数t是否达到规定的最大值，如果未达到，返回到步骤②中，否则输出最优解。

（2）子群内部局部更新

子群内部局部更新主要是对每个子群中适应度值最小的青蛙个体位置更新。

①k表示子群内部迭代次数，初始值设为0；

②对k进行加1操作，然后根据适应度值大小得到该子群中适应度值最大和最小的青蛙个体。

③对子群中具有最小适应度值的青蛙个体进行更新，更新策略如下所示：

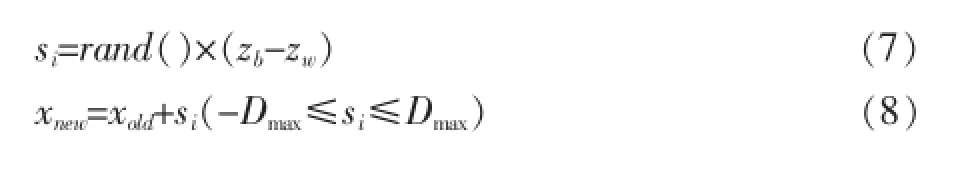
其中rand（ ）函数产生一个范围在0～1之间的随机数，S表示青蛙个体的移动步长，Dmax表示青蛙允许移动的最大距离。

④根据更新结果调整对应的更新方式

如果上述过程能够产生一个更优解，即能够产生一个适应度值更大的个体，那么用新位置的青蛙取代原来该子群中拥有最小适应度值的青蛙个体，否则，用Gb代替Fb，即步长公式变为：

对最差个体重复上述更新过程。如果仍然不能产生一个更优解，那么随机产生一只青蛙代替该子群中适应度值最小的青蛙个体。

⑤子群局部更新结束条件判断

若迭代次数k满足最大值，返回执行（1）中的步骤③，否则返回执行（2）中的步骤③。

2.2 改进SFLA算法

基本蛙跳算法的局部更新过程即基于最优青蛙个体影响最差青蛙个体的方式去更新子群中的最差个体。该过程首先基于各子群内部适应度值最大和最小的青蛙个体对适应度值最小的青蛙个体进行更新，如果产生的新个体不是更优解，即适应度值更大，那么我们重新基于群体适应度最大值对位置最差的青蛙个体进行更新，如果产生的新个体仍然不是最优解，那么我们随机产生一个新个体代替原来子群内部适应度值最小的个体。

在此基础上，本文对传统混合蛙跳算法进行了如下两点改进：

（1）首先考虑在局部更新的过程中，同时基于子群内部以及整个种群适应度值最大个体去更新各子群内部适应度值最小个体，从而避免陷入局部最优，并且，通过这样的改进还可以减少算法的运行时间。即使用一种新的步长计算公式：

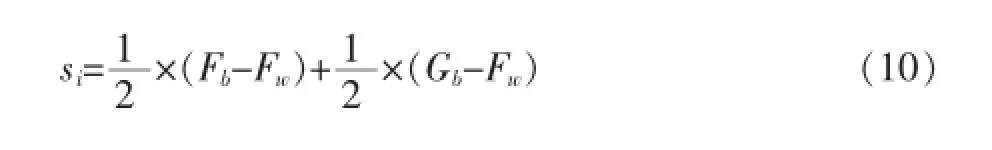
（2）其次，本文提出了新的青蛙个体更新公式，以更新各子群内最差青蛙个体的位置。新公式如下所示：

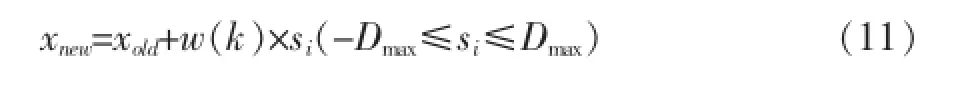
设w（k）是一个随着子群内部迭代次数k的增加而逐渐减少的函数。w（k）=（kmax-k+rand（ ）），由此可知，早期迭代中大的w（k）值可以扩大解空间的搜索范围，即增加解决方案的多样性，而后期迭代中小的w（k）值使得算法在局部范围内搜索更优解，即进一步提高局部搜索的能力。

2.3 ISFLA优化LSSVM的短时交通流量预测模型

本文改进的混合蛙跳算法（ISFLA）优化LSSVM模型中参数的步骤如下所示：

（1）初始化基本参数，如青蛙的数目L，子群数目m，子群内部迭代次数k，全局迭代次数t，最大迭代次数kmax，全局最大迭代次数tmax，青蛙个体允许移动的最大距离Dmax；

（2）每只青蛙个体的位置对应一组LSSVM的正则化参数和核参数（γ，σ），计算所有青蛙的适应度值并记录全局最优解。我们设置精确度PRE为适应度函数，每个青蛙个体根据适应度函数值进行优劣排序并且分成子群。

（3）对每个子群的适应度值最小的青蛙个体先按公式（10）和（11）进行更新，如果新位置的青蛙个体适应度值大于原来的适应度值，则更新后的青蛙个体替换原来适应度值最小的青蛙，否则仍随机生成一个新青蛙个体替代原子群中适应度值最小的青蛙个体，重复上述过程，直到满足子群内部最大迭代次数。

（4）混合所有子群，对所有青蛙个体按适应度值大小进行重新降序排序。

（5）如果终止条件不满足，返回第（2）步，否则输出最大的适应度值的青蛙所在的位置，即最优的LSSVM参数对（γ，σ）。

改进蛙跳算法优化LSSVM的步骤示意图如图1所示：

图1 改进蛙跳算法优化LSSVM示意图

3 仿真结果分析

3.1 数据来源

本文中数据来源于2012年四川省某段高速公路，搜集了从7月15日至22日的每天早9点到晚8点每15分钟的流量，得到48×8=384个数据。用前7天的数据作为训练集训练模型，而后1天的数据作为测试集以验证模型的预测效果。

显然当前交通流量与历史交通流量之间有着明显的联系。v（t）表示t时刻的交通流量，v（t-1）表示t-1时刻的交通流量，我们使用当前时刻以及历史时刻的交通流量来预测下一时刻的交通流量，如下所示：

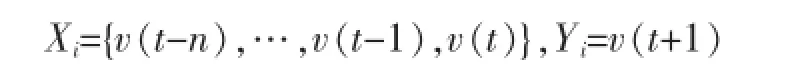
其中Xi表示系统的输入，Yi表示系统的输出。本文中我们设置n为6。

3.2 参数设置

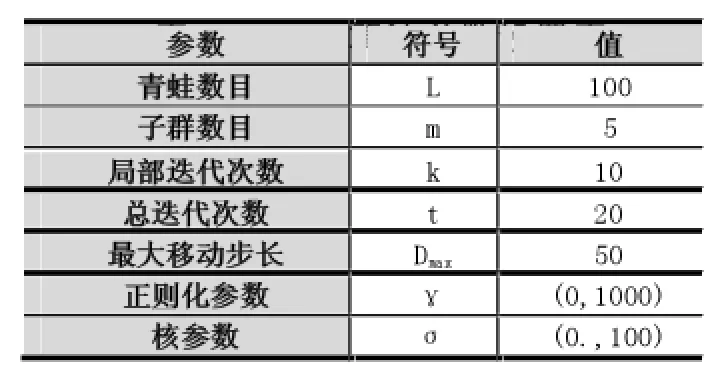
为了验证ISFLA-LSSVM模型在短时交通流量预测中的有效性，进行了如下三种实验：（1）采用改进后的混合蛙跳算法（ISFLA）优化后的LSSVM模型进行预测；（2）采用传统SFLA算法优化后的LSSVM模型进行预测；（3）采用网格搜索算法（GS）优化后的LSSVM模型进行预测。实验（1）中算法参数设置如下所示：γ的范围为（0，1000），σ的范围为（0，100），青蛙数目设置为100，子群数目设置为5，子群内部迭代次数设置为10，总迭代次数设置为20，最大移动步长设置为50。实验（2）的参数设置与实验（1）一样。实验（3）的参数设置则如下所示：迭代截止误差为10-3，γ和σ的搜索范围同上，步长设置为10。

?

3.3 评价指标

为了验证所提出的模型的有效性和优越性，使用如下指标作为模型预测性能的评价指标：MRE、RMSE和精确度PRE。

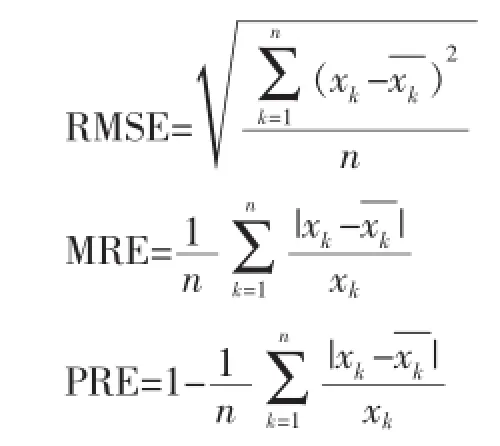
其中xk是预测值是实际值。这三个指标反映了模型的误差和预测能力，RMSE和MRE的值越小，精确度PRE的值越大，表明模型的预测性能越强。

3.4 实验结果分析

通过ISFLA算法优化LSSVM参数我们可以构造基于ISFLA-LSSVM的短时交通流量预测模型。LSSVM根据改进混合蛙跳算法、蛙跳算法、网格搜索算法找到的最优参数建立的短时交通流量预测模型预测值与实际值示意图如图2所示。

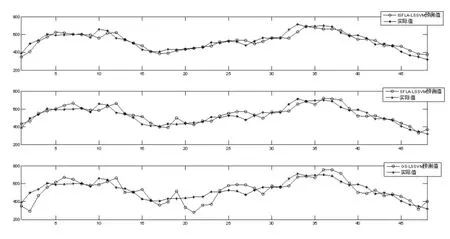
图2 不同方法流量预测示意图

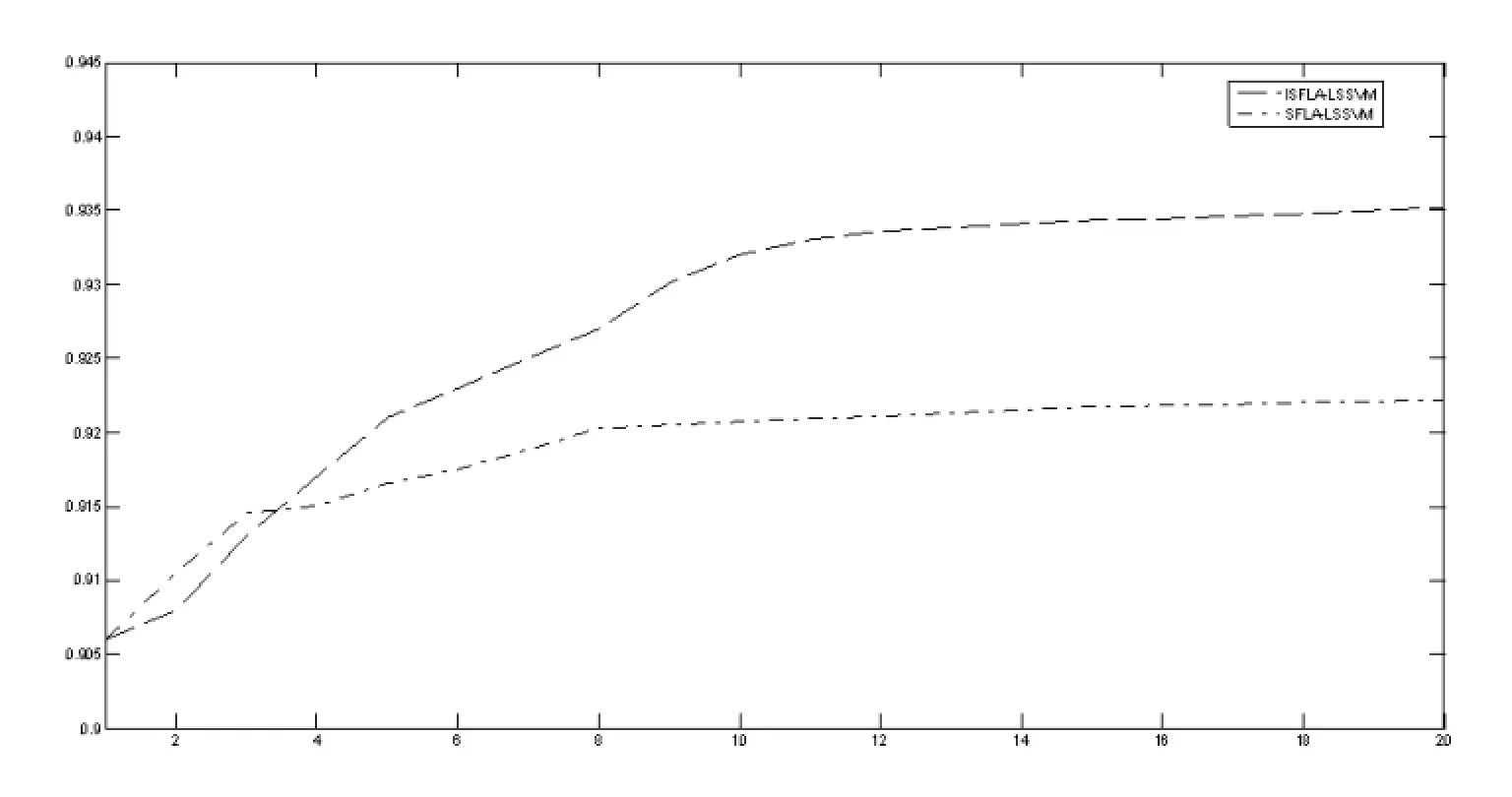
图3 ISFLA与SFLA的迭代寻优图

由图2可知，三种预测模型中ISFLA-LSSVM的预测值与实际值偏差最小，预测结果最好。

表1为三种预测模型的预测结果对比，从表1我们可以看出，ISFLA-LSSVM模型的MRE和RMSE最小，分别为0.058以及39.60，明显低于SFLA-LSSVM模型以及GS-LSSVM模型。精确度最高，为94.13。因此，与其他两种模型相比，本文提出的ISFLA-LSSVM模型是最优的。

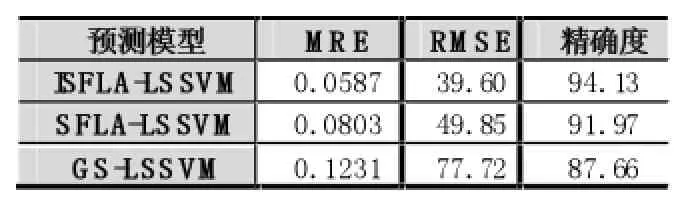
表2 不同方法预测结果表

图3描述了基于改进混合蛙跳算法和传统混合蛙跳算法优化最小二乘支持向量机在迭代寻优次数为20次时的适应值变化过程。

由图3可知，与基本混合蛙跳算法相比，本文提出的改进蛙跳算法迭代初期全局搜索能力较强，不易陷入局部最优，迭代后期局部搜索能力较强，收敛效果较优，寻优结果较好。

4 结语

传统混合蛙跳算法容易陷入局部最优，本文通过对该算法局部更新策略进行修改，提出了改进混合蛙跳算法（ISFLA）。改进后的算法较好地平衡了全局搜索能力和局部更新能力，不易陷入局部最优。并且针对短时交通流量预测中使用最小二乘支持向量机模型时参数难以选择的问题，本文使用ISFLA算法对其中的参数进行优化，提出了ISFLA-LSSVM短时交通流量预测模型。通过实例证明，与参比模型相比，改进后的预测模型有较高的预测精度，适合应用于短时交通流量预测。

[1] 沈国江，王啸虎，孔祥杰.短时交通流量智能组合预测模型及应用[J].系统工程理论与实践，2011，31（3）：561～568

[2] Bidisha Ghosh，Biswajit Basu，Margaret O'Mahony.Multivariate Short-term Traffic Flow Forecasting Using Time-series Analysis[J]. IEEE Transactions on Intelligent Transportation Systems，2009，10（2）：246～254

[3] 董春娇，邵春福，熊志华，李娟.基于Elman神经网络的道路网短时交通流预测方法[J].交通运输系统工程与信息，2010，10（1）：145～151

[4] 姚智胜，邵春福，等.基于主成分分析和支持向量机的道路网短时交通流量预测[J].吉林大学学报（工学版），2008，38（1）：48～52

[5] Huang Xiaolin，Shi Lei，Suykens，Johan A.K.Support Vector Machine Classifier with Pinball Loss[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，2014，36（5）：984～997

[6] 赵亚萍，张和生等.基于最小二乘支持向量机的交通流量预测模型[J].北京交通大学学报，2011，35（2）：114～117

[7] GAO Junwei，LENG Ziwen，ZHANG Bin.Traffic Flow Forecasting Based on Phase Space Reconstruction and PSO-LSSVM[J].ICIC Express Letters，2014，8（1）：63～70

[8] 陈帅，朱建宁，潘俊，侍洪波.最小二乘支持向量机的参数优化及其应用[J].华东理工大学学报（自然科学版），2008，34（2）：278-～282

[9] ZHU Guangyu，ZHANG Weibo.An Improved Shuffled Frog-leaping Algorithm to Optimize Component Pick-and-Place Sequencing Optimization Problem[J].Expert Systems with Applications，2014，41（15）：6818-6829.

[10] 郑仕链，楼才义，杨小牛.基于改进混合蛙跳算法的认知无线电协作频谱感知[J].物理学报，2010，59（5）：3611～36

Short-term Traffic Flow Forecasting Based on Improved LSSVM

LOU Wan-qiu
（Department of Computer Science，Sichuan University，Chengdu 610065）

To improve the predicting accuracy,proposes a short-term traffic flow forecasting model which is based on the improved least square support vector machine.Proposes an improved algorithm based on the traditional shuffled frog leaping algorithm,which can let shuffled frog leaping algorithm be not easy to fall into local optima.Uses the ISFLA algorithm to determine the important parameters in LSSVM, which significantly influences the predicting performance in the model.Simulation analysis demonstrates the feasibility of the model and the effectiveness of the algorithm.

Short-Term Traffic Flow Forecasting;Least Square Support Vector Machine;Improved Shuffled Flog Leaping Algorithm;Parameter Selecting;Intelligent Optimization Algorithm

1007-1423（2015）04-0003-06

10.3969/j.issn.1007-1423.2015.04.001

娄婉秋（1991-），女，贵州安顺人，研究生，研究方向为智能交通

2015-01-08

2015-01-20

国家自然科学基金（No.11102124）