初中数学发生教学法的策略与应用——以北师大版“字母表示数”为例

☉华中师范大学教育学院 张俊忠

初中数学发生教学法的策略与应用
——以北师大版“字母表示数”为例

☉华中师范大学教育学院 张俊忠

德国生物学家海克尔在1866年提出了“生物发生原理”，即“个体发育史重蹈种族发展史”.将此类推于数学教育将得出：个体对数学知识的理解过程遵循数学知识的发生、发展过程.把数学史作为教学线索，不明确地谈论数学史，用数学史来启示教学，这就是数学发生教学法.

一、发生教学法的策略

运用发生教学法进行教学设计的关键在于教师，对教师的要求是：（1）要全面了解所教主题的历史；（2）要理解该主题历史发展过程中的关键环节；（3）掌握一个环节发展到下一个环节的原因是什么，遇到的困难和障碍是什么；（4）重构历史环节，使其适合于课堂教学；（5）设计出一系列由易到难、环环相扣的问题.

具体实施时，可以分为四个阶段.（1）创设问题情境：思维和认知过程的起源是构造问题情景的最佳方式；（2）自然引出新问题：思考和理解的第一步是产生问题，而且每解决一个问题就会产生新的问题，在解决了最初的问题之后，还需要不断思考新的、自然出现的问题；（3）分析学生的认知需求：确定学生思维能力的水平，估计过程中可能存在的困难，重要的是寻求激发学生学习动机的方法；（4）重构历史顺序：在现代教学背景下重构关键的思想和问题，以发生的历史过程解释概念、理论或关键思想后面的动机.

二、发生教学法的应用

以北师大版七年级数学上册第三章“整式及其加减”第一节“字母表示数”为例，介绍发生教学法的具体过程.

（一）全面了解“字母表示数”的历史

19世纪德国数学史家内塞尔曼在《希腊代数》中将代数学的发展分成三个阶段：修辞代数、缩略代数和符号代数.

修辞代数阶段，人们没有使用符号表示数，所有问题的解决都用文字来说明，如古巴比伦泥版BM13901上有七个问题，其中第1题是：“将正方形面积与边长相加，和为，求边长.”解法是：置系数1，半之，得乘，得相加，得1；此为1的平方，从1中减去即为正方形边长.”

在古希腊，毕达哥拉斯学派（公元前六世纪）研究了多边形数，数学家们能轻易说出一个具体的多边形数.由于不知道字母表示数，他们无法表达“任一三角形数”.同样数列的“通项”概念在修辞代数里是根本不存在的，所有数列求和的结果都是针对具体的若干项.古代两河流域、阿拉伯的代数学均属于修辞代数.

公元三世纪，古希腊数学家丢番图在《算术》中首次用字母“ζ”来表示未知数，于是丢番图成为缩略代数最早的作者.在《算术》第1卷中，第1题是：“已知两数的和与差，求这两个数.”丢番图的解法是：假设和为100，差为40，较小数为ζ，则较大数为40+ζ，则2ζ+40=100，故得ζ=30，而较大数为70.后来，使用不同的字母表示不同的数，但是可以看到字母总是表示未知数.由于不知道用字母也可以表示任意已知数，丢番图只能用特殊的数来代替题中的已知数.

古代印度数学家使用缩略的梵文音节来表示未知数，没有用缩略音节来表示任意数（包括已知数和未知数）.如印度数学家婆什伽罗（1114-1185年）和古希腊数学家一样，不会用字母来表达“任意多项”和一般项，只是取一些特殊的项数，且通项公式和求和公式都是用文字来描述，因此古代印度的代数属于缩略代数.

中国宋元时期的数学家使用“天元”来表示未知数，“二元一次方程”中的“元”指的就是未知数.在“天元术”中，通过系数的纵向有序排列来表达多项式，在常数项右边标一“太”字，或只在一次项系数的右边标一“元”字，中国宋元时期的“天元术”最多也只能归入缩略代数.

公元十六世纪，法国数学家韦达（1540-1603年）实现了历史性的突破，在《分析引论》（1591年）中使用字母来表示未知数和已知数.他说：“本书将辅以某种技巧，通过符号来区分未知量和已知量：用A或其他元音字母I、O、V、Y等来表示所求量，用B、G、D或其他辅音字母来表示已知量，始终如一，一目了然”，并将这种新的代数叫“类的算术”，以区别于过去的“数的算术”，“类的算术”就是符号代数.规定了算术与代数的分界，认为代数运算施行于事物的类或形式，算术运算施行于具体的数.这就使代数成为研究一般类型的形式和方程的学问.法国数学家笛卡尔（1596-1650年）对韦达的符号系统进行了改进.

（二）“缩略代数”到“符号代数”是关键

“缩略代数”阶段以字母表示未知数为典型特征，丢番图是这一时期的典型代表人物.随后印度数学家阿里耶波（476-550年）等虽朝向“符号代数”有所接近，但只在字母表示数的类型与方程解的一般性上做出了贡献，而不是尝试表达“任意数”.在丢番图之后一千多年间，欧洲人不仅没有进步，反而倒退回古巴比伦祭司的水平，即修辞代数阶段.如13世纪初，意大利数学家斐波纳契在《计算之书》中，依然没有用字母来表示数.16世纪，意大利数学家尽管在方程的求解上取得突破，但仍未利用字母表示数的便利.塔塔里亚（1499-1557年）为了不遗忘所发现的三次方程求根公式，自编长诗.

中世纪阿拉伯的数学家尽管在数列求和方面取得了卓越的成就，但是他们不会用字母来表示数，他们只能通过具体的若干项来说明求和的方法.虽然“代数学”的名称源于花拉子米（约780-约850年）的著作，而花拉子米却用“1平方与10根等于39单位”这样的语言来描述一元二次方程x2+10x=39.

“字母表示数”经历了三千多年的历史过程，经过许多数学家的探索和完善.诚如M.克莱因对“新数运动”的批判：从古代埃及人和巴比伦人开始直到韦达和笛卡儿以前，没有一个数学家能意识到字母可用来代表一类数.因此，这样的过渡仍然需要经历缓慢的过程而非一蹴而就.

（三）学生学习的障碍和困惑

在长期的算术学习中，学生形成的认知与代数学习有较大的差别，“字母表示数”意义的多样性与不确定性是造成学生学习代数的主要障碍.字母意义的演变过程为：记数符号—未知数—任意数.随着人们对字母意义认识水平的提高，字母表示数的功能逐步得到发展与完善，这是一个漫长的过程.因此学生在学习“字母表示数”的时候会遇到许多困难，主要表现为：不同字母可以取同一个值；同一个字母在不同时刻可以取不同的值；同一字母在不同问题中可以取不同的值；在同一题中不同的数要用不同字母表示；字母不一定表示对象，也可以表示单位（如m可以表示米）等.

（四）根据历史，重构课堂

1.创设情境，引入新知

情境1：写一列数“1，5，9，x，17，21”，请问：x表示什么数？让学生体会，在以前的学习中，字母更多地表示特定的未知数.

情境2：例如，一只白兔四条腿，两只白兔八条腿……

师：你们能一直读下去吗？

生1：三只白兔十二条腿，四只白兔十六条腿……

师：能不能用一句话表示这首歌？

生2：a只白兔4×a条腿.

生3：b只白兔4×b条腿.

生4：x只白兔4×x条腿.

师：大家的想法比较一致，用字母表示.为什么这里的“4”不用字母表示？

生4：每只白兔有4条腿，这是不变的.

师：用字母表示数不是简单地用字母代替数，可以把变化的量用字母表示，不变的量照写.

师：刚才我们说的十二、十六都是其中的一种情况，那现在的“4×x”呢？

生5：所有的情况.

生6：各种不同的情况.

师：这里的字母表面上看只是一个字母，但是它可以代表无数个数.

师：回想一下刚才我们所经历的过程，你觉得字母只是代表特定的未知数吗？

生：不是.

师：那现在代表什么？

生7：不是特定的.

生8：不确定了.

生9：是变化的.

生10：表示许多数了.

师：对！现在字母表示的是变化的未知数.此时的字母可以表示任意数吗？

生11：不可以.

师：对，只能是什么数？

生11：正整数.

师：那字母还只是表示未知数吗？

生11：不只是，可以表示已知数了.

师：既然是已知数，为什么还要用字母表示？

生11：因为正整数很多，我们不能确定它到底是多少.

生12：因为它有很多个.

师：这样的数太多了，用一个字母把它们都概括进来了.由此可知，字母可以表示：特定的未知数、变化的未知数、已知数.

2.自主探索，展示过程

师：我们来数由正方形组成的几个图形中火柴棒的根数！

师：这些图形中分别有多少根火柴棒？

生1：4根、7根、10根、……

师：如果摆10个这样的小正方形，又有多少根火柴棒？

生2：31根火柴棒，我是画图一根一根数出来的.

师：很好，你完成得很认真.还有其他的方法吗？

生3：如果有200个这样的正方形，我们画图形去数，这方便吗？这个方法肯定不是最科学的.我认为应该寻找规律，这个问题就像我们锯木材：每个正方形相当于一段木头，而除了两端的两根火柴棒外，中间的都相当于锯口，而且锯口数正好是木头段数减去1.所以应该用4乘以正方形个数再减去重叠的火柴棒的根数，就是4× 10-（10-1）＝31.

师：还有其他的方法吗？

生4：我还有另一种方法，结果也得31.

师：说说你的看法！

生4：既然有10个这样的正方形，那么上面应有10根火柴棒，下面也有10根，而中间的算法与之类似，不过应该比木头段数多1，是11根，这样2×10+11＝31.

师：大家听懂了吗？

生众：听懂了.

生5：我认为他们的办法太麻烦了.既然是10个正方形组成的图形，用手把最左边的那根火柴棒盖上不看，右边就是10个由3根火柴棒组成的框，就是10×3，再加上1根，这样10×3+1=31.不论由多少个正方形组成的图形，用这种方法都能算出来，就是用3乘以正方形个数再加上1.

师：你们的想法都很不错.既然你们谈到任何多个正方形组成的图形，那么我们怎样表示任何多个正方形呢？

生6：任何多个，就是大家也不知道有多少个，用小学时学过的x吧！

生7：我们还可以用m、n、….

师：如果摆x个正方形，那么需要多少根火柴棒？

生3：按我的方法，应该是4x-（x-1）.

生4：按我的想法，应该是2x+（x+1）.

生5：按我的想法，应该是3x+1.

师：这三种方法都表示了这个问题的结论，用字母表示的好处是什么？

生8：这样更具有一般性.

师：那么以前我们学过的加法交换律、结合律，乘法交换律、结合律，简单图形的周长、面积公式，可以用字母表示吗？

生：当然可以，不过要用到很多字母.

3.拓展延伸，巩固新知

师：下面的练习是“编故事”.故事的主角是“a×5”.如果a表示一张桌子的重量，那么a×5表示什么意义？

生1：5张桌子的重量.

师：而且是5张同样的桌子的重量.哪个同学来编？

（学生们用a代表各种数量，说了“a×5”的含义）

师：大家把“a×5”讲得这样丰富多彩，老师也来讲个这方面的历史故事.

师：在历史上，数量和数量之间的关系，我们人类最初是用文字表达的（如：每张重量×5，每段长度×5，每组人数×5）.用文字来表达，显然比较烦琐.因而，古希腊数学家丢番图想到了用“缩略”的方法来表示.仿照丢番图的方法，这里的“每个重量×5”，取“重”发音的第一个字母，表示成“z×5”.那么“每段长度×5”和“每组人数×5”怎样用缩略的方法表示？

生2：c×5和r×5.

师：丢番图用字母的缩略形式来表示数量间的关系，虽然简洁了，但每个字母都表示特定的意思，不能把c×5和r×5等同，所以并没有给研究数学带来更多方便.到了16世纪，法国数学家韦达想，如果把各种情境中字母的特定意思都去掉，不都是一个数和5相乘吗？所以韦达就表示成了a×5.这里的a还是特定的意思吗？

生众：不是！

师：对，字母a已经不表示任何具体的意义，只是一个符号而已.自从韦达把字母当作符号来表示数之后，许多数学难题得到解决，数学获得飞速发展，韦达被称为现代代数学之父.

4.实践应用，归纳小结

例1（1）若长方形的长为7cm，宽为xcm，则周长为_______cm，面积为_______cm2.

（2）甲、乙两地相距s千米，某人从甲地到乙地步行要t小时，现要求他提前30分钟到，此人步行的速度为_______千米/时.

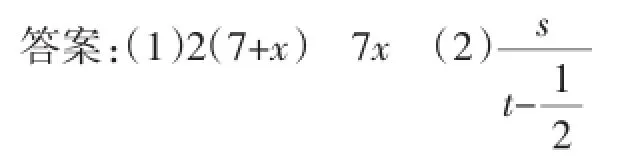
例2已知两个数的和与这两个数的差，求这两个数.

补充：修辞代数解法：其中一个数是和与差的和的一半，另一个数是和与差的差的一半.

缩略代数的解法：以丢番图的解法为代表.设和为100，差为40，较小数为x，则较大数为x+40.这样就有x+x+ 40=100，从而得x=30，30+40=70，因此两数分别为70、30.

符号代数的解法：以韦达的解法为代表.设和为a，差为b，又设较小数为x，则较大数为x+b，于是x+x+b=a，故得因此两数分别为

（五）总结

1.用字母表示数的特点

字母表示数更能反映事物的一般性；字母的取值应使式子有意义且符合实际情况.

2.字母表示数时应注意的问题

同一问题中，不同的量要用不同的字母表示；不同的问题中，不同的量可以使用相同的字母表示，但字母的含义不同.

（六）作业

P79：1，2，P80：3.

1.涂荣豹，宁连华.中学数学经典教学方法［M］.福州：福建教育出版社，2011.

2.郑毓信，王宪昌，蔡仲.数学文化学［M］.成都：四川教育出版社，2001.

3.李文林.数学史教程［M］.北京：高等教育出版社，施普林格出版社，2000.

4.李迪，主编.中外数学史教程［M］.福州：福建教育出版社，1993.