钢筋混凝土圆柱等效阻尼比及在桥梁抗震分析中的应用
张艳青,贡金鑫,张 勤,韩 石
(1. 大连理工大学 土木工程学院结构工程研究所,辽宁 大连 116024;2. 河海大学 土木与运输工程学院结构工程研究所,南京 210098)
钢筋混凝土圆柱等效阻尼比及在桥梁抗震分析中的应用
张艳青1,贡金鑫1,张 勤2,韩 石1
(1. 大连理工大学 土木工程学院结构工程研究所,辽宁 大连 116024;2. 河海大学 土木与运输工程学院结构工程研究所,南京 210098)
基于对50根弯曲破坏钢筋混凝土圆柱低周反复试验结果的分析,建立了完整滞回环的数学表达式并推导得出等效阻尼比计算模型;以双柱墩桥梁为例,说明了建立桥梁整体结构等效阻尼比与墩柱端部塑性铰等效阻尼比关系的方法。研究表明,完整滞回环数学表达式较好地反映了弯曲破坏钢筋混凝土圆柱的滞回特性,得到的等效阻尼比模型计算结果与试验结果符合较好;采用建立的桥梁整体结构等效阻尼比与墩柱端部塑性铰等效阻尼比的关系进行pushover分析更能反映实际情况。采用等效阻尼比模型算得的目标位移与基于Rosenblueth模型和Kowalsky模型算得的位移之间存在较大差距。
钢筋混凝土;圆柱;弯曲破坏;滞回环;等效阻尼比
非线性静力弹塑性分析方法是近年来结构抗震分析常用的一种方法[1-6],能力谱法是该方法中的一种。此类方法将结构等效为一个单自由度体系,采用等效割线刚度和等效阻尼比,结合地震反应谱计算规定地震下结构的最大反应位移。等效阻尼比的合理确定非常重要。
关于等效阻尼的确定,众多学者已进行了大量研究。Jacobsen[7-8]最早针对弹塑性单自由度体系提出了等效粘性阻尼的概念,其成果对等效阻尼比的研究产生了重要意义。Rosenbluethn等[9]将实际的荷载-位移关系简化为Kinematic双线型模型,基于Jacobsen的等效粘性阻尼概念,利用一个运动循环滞回曲线所围成的面积与阻尼消耗的能量相等的关系确定等效阻尼比。Kowalsky[10]将该方法用于Takeda[11]提出的具有卸载刚度退化特征的滞回模型,将卸载刚度系数取为0.5,确定了等效单自由度体系的等效阻尼比计算模型。Gulan等[12]根据小比尺钢筋混凝土框架结构的振动台试验结果,结合Taketa等[11]滞回模型提出了等效阻尼比模型。Iwan等[13]利用库仑滑移单元和弹性单元得到的滞回模型,根据12条地震波作用下的时程分析结果,得出了等效阻尼比模型。Kwan等[14]根据Iwan所提出的方法研究了6种滞回模型、20条地震波、周期范围在0.1~1.5 s的等效阻尼比模型和等效周期关系式,所提出的等效阻尼比模型中考虑了滞回模型的影响。中国也有学者从不同角度对等效阻尼比进行了研究[15-19]。马恺泽等[20]在统计分析的基础上,提出了考虑场地类别和设计地震分组的等效阻尼比模型。陆本燕等[21]通过对不同研究者提出的等效阻尼比模型进行对比研究指出,滞回模型对等效阻尼比有很大影响。
按照能量相等原理得到的等效阻尼比是针对一个构件塑性铰的,并不适用于有多个塑性铰的结构(尽管目前仍这样做);通过地震数值分析得到的经验等效阻尼比公式是针对所分析情况的,当实际结构与所分析结构不同时,采用这种等效阻尼比是不合理的。
本文对项目组16根[22]和PEER数据库中34根[23]弯曲破坏的圆形截面钢筋混凝土柱低周反复试验试验结果进行了分析,建立了滞回环的数学模型,推导得出构件的等效阻尼比计算公式;以双柱墩桥梁为例,建立了桥梁整体结构等效阻尼比与墩柱端部塑性铰等效阻尼比的关系式。阐述了本文等效阻尼比公式在钢筋混凝土双柱墩桥梁抗震pushover分析中的应用。
1 滞回环模型
1.1 曲线上的特征点
设计制作了16根圆形截面钢筋混凝土试件,试件截面直径为235 mm,混凝土保护层厚度为20 mm,剪跨比为6和7,如图1所示。混凝土强度等级为C40,实测混凝土立方体抗压强度51.39 MPa,弹性模量3.66×104N/mm2。纵筋采用HRB335级钢筋,采用8φ16和6φ12 mm两种配筋方式,对应的配筋率为3.7%和1.56%,沿试件周边均匀布置。箍筋采用直径6.5 mm的HPB235级钢筋,间距分别为50、100 mm,对应的配箍率分别为0.28%和0.56%,主要试验参数如表1所示。
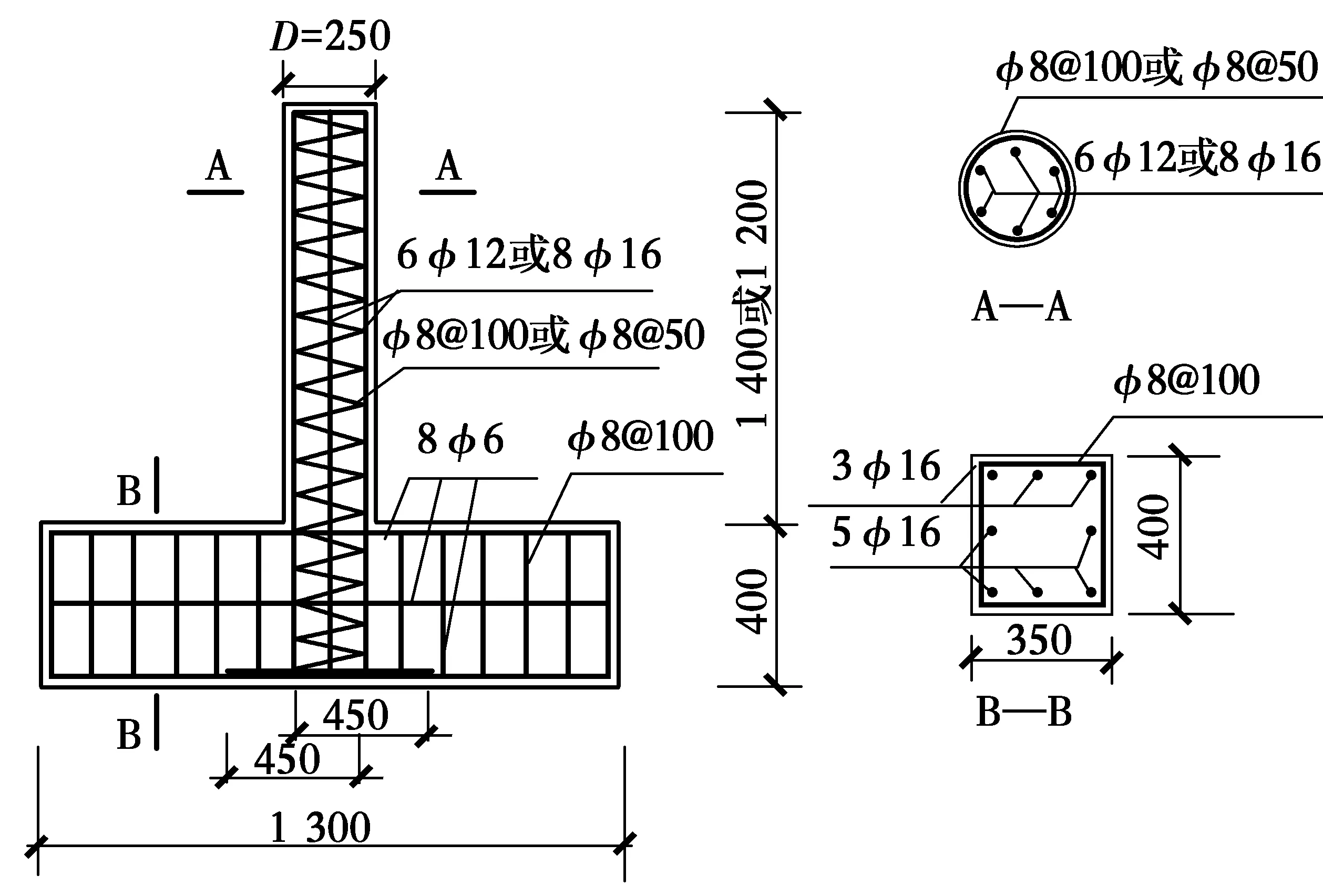
图1 试件截面尺寸和配筋(单位:mm)Fig.1 Dimensions and reinforcements of column specimens(Unit:mm)
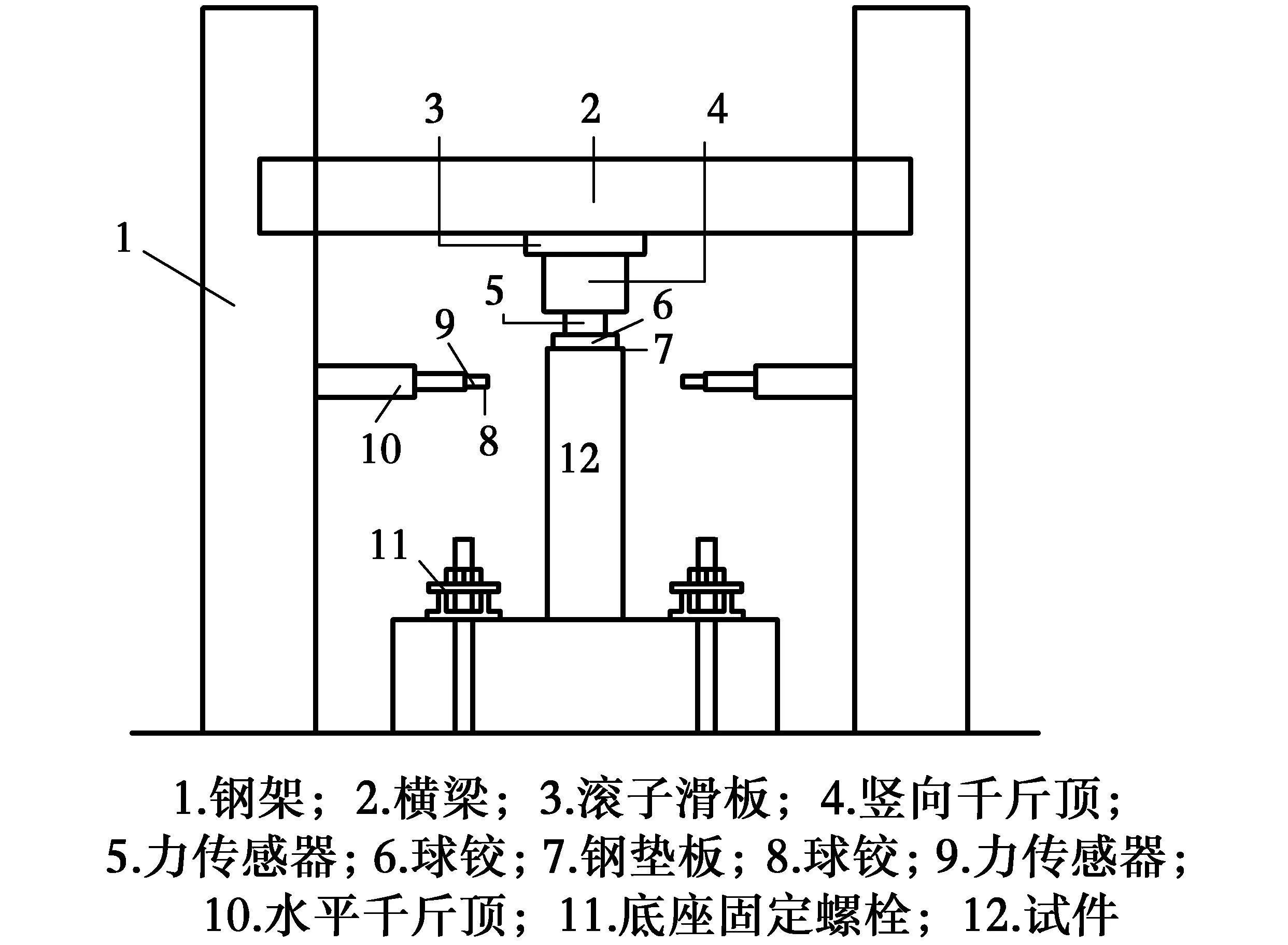
图2 试验加载装置Fig.2 Details of test setup
试验在大连理工大学结构工程实验室进行,采用悬臂梁式拟静力加载方法加载,如图2所示。首先利用液压千斤顶在试件顶部施加恒定的竖向荷载,千斤顶通过滚子滑板与反力架横梁相连,以确保千斤顶与试件一起平动。试件顶部水平荷载通过固定于两侧反力架上的液压千斤顶施加。试验采用位移控制,开始加载时变形为2 mm,3个循环后按照4 mm的倍数递增,每级循环3次,直到试件发生严重破坏而无法承受轴力。试验加载制度如图3所示。试验测量的主要参数包括:柱顶水平加载点处的水平荷载和位移;沿柱试件高度一定范围内的弯曲、剪切变形及塑性铰区段的转角;纵向钢筋和箍筋应变等。仪表和应变测点布置如图4所示。所有荷载、位移和应变均采用32通道的德国imc数据采集系统采集。

图3 水平荷载加载制度Fig.3 Horizontal displacement history
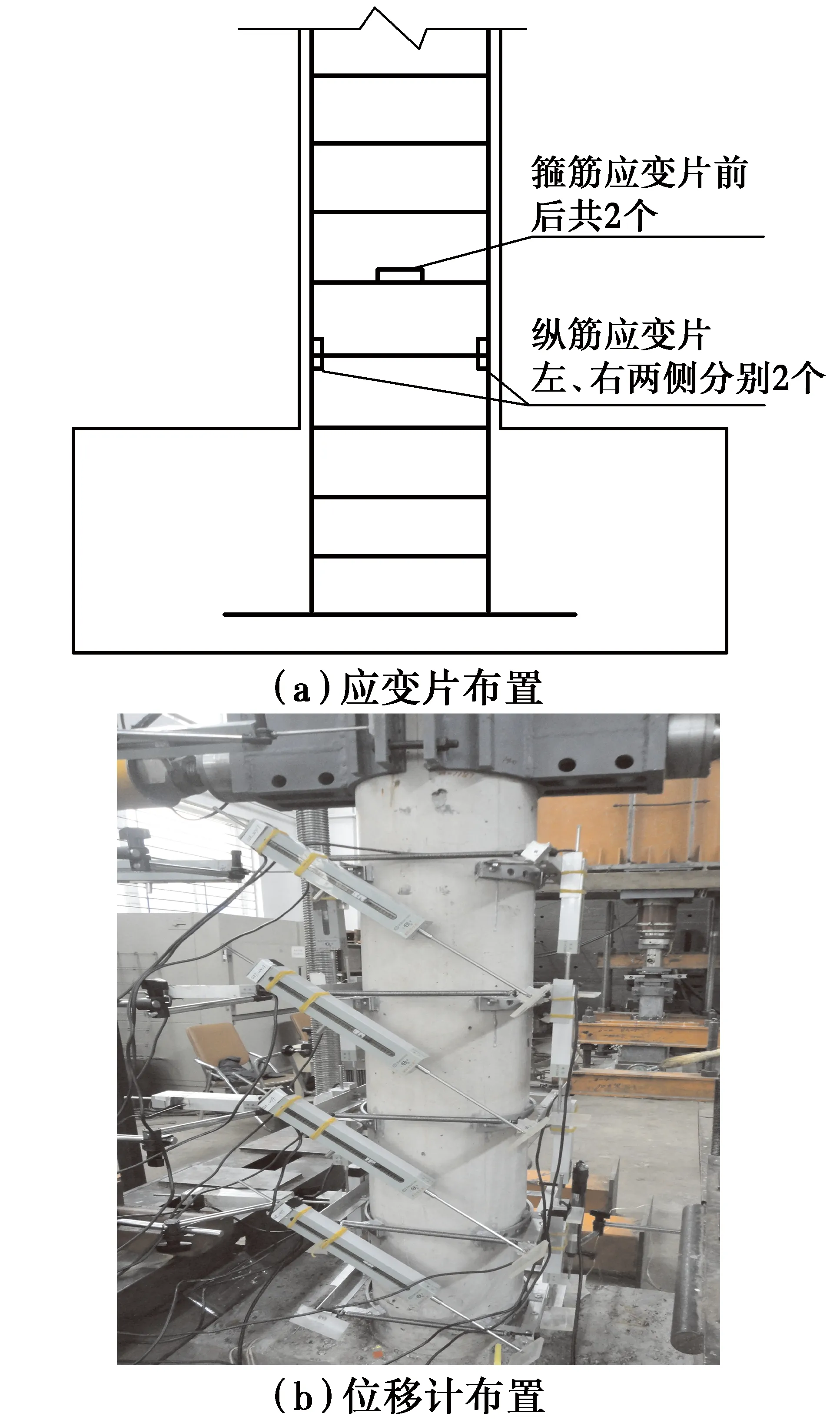
图4 位移计和应变仪布置图Fig.4 Layout of instruments and strain gauges
所选PEER数据库中34根弯曲破坏圆形截面钢筋混凝土柱的主要试验参数同样列于表1中,表中所有试件均为低周反复加载。

表1 试件试验参数Table1 Parameters of specimens
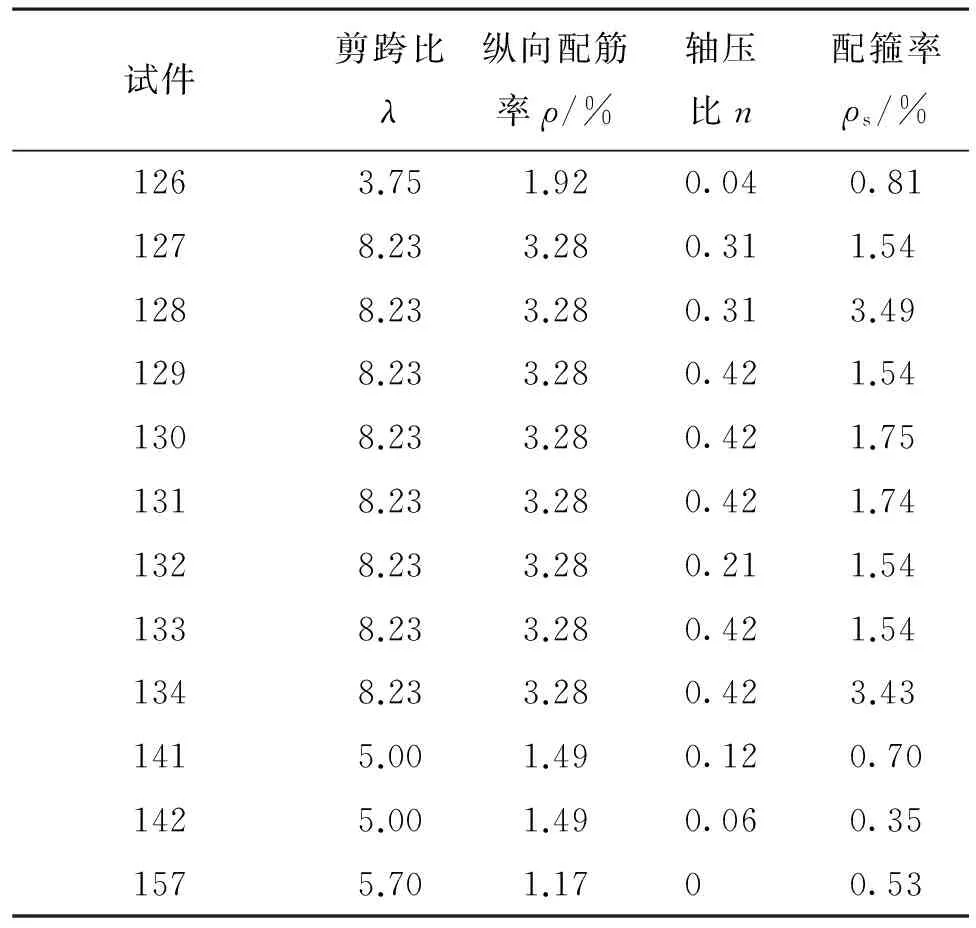
续表1
注:C表示圆柱,第1个数字表示剪跨比,计算为柱的剪跨与截面有效高度的比值,截面有效高度为截面直径的0.8倍;第2个数字表示纵向配筋;第3个数字表示轴压比;第4个数字表示箍筋间距。例如,C7-6L12-50-0.2表示试件的剪跨比为7,纵向配置6根12 mm的钢筋,箍筋间距为50 mm,轴压比为0.2。
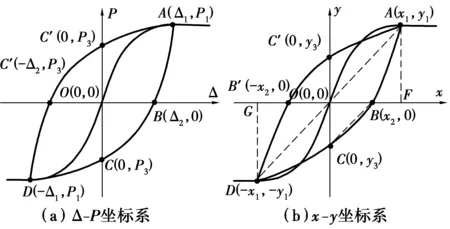
图5 滞回环Fig. 5 Hysteretic loop for one cycle
试验表明[22-23],对于箍筋约束良好、以弯曲破坏为特征的圆形截面偏心受压试件,滞回环比较饱满,呈外凸型,没有捏缩现象,可以表示为图5(a)所示的形式。曲线关于原点对称,A、B、B′、C、C′和D为滞回环上的6个特征点,其中,点A(Δ1,P1)和点D(-Δ1,-P1)为滞回环在正、反加载方向上位移最大的点,位于滞回曲线的骨架曲线上,点B′(-Δ2,0)和点C′(0,P3)为曲线上半环与Δ轴(变形)和P轴(荷载)的交点,点B(Δ2,0)和点C(0,-P3)为曲线下半环与Δ轴(变形)和P轴(荷载)的交点。为了能够将所有试件表示在同一个坐标系下,采用图5(b)所示的无量刚形式确定滞回环上的特征点,该图中,x=Δ/Δy;y=P/Py,屈服点Y(Δy,Py)采用图6所示的能量法计算得到。对文献[22]的16根试件和PEER数据库[23]中34根试件的滞回环数据进行分析,得到x2与x1的关系如图7所示。对50根试件的滞回环数据进行拟合,得到关系式
x2=0.765×(x1-1)1.074
(1)
图8所示为所选50根试件的滞回环上y3/x2与y1/x1关系图,拟合得到其关系式
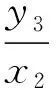
(2)
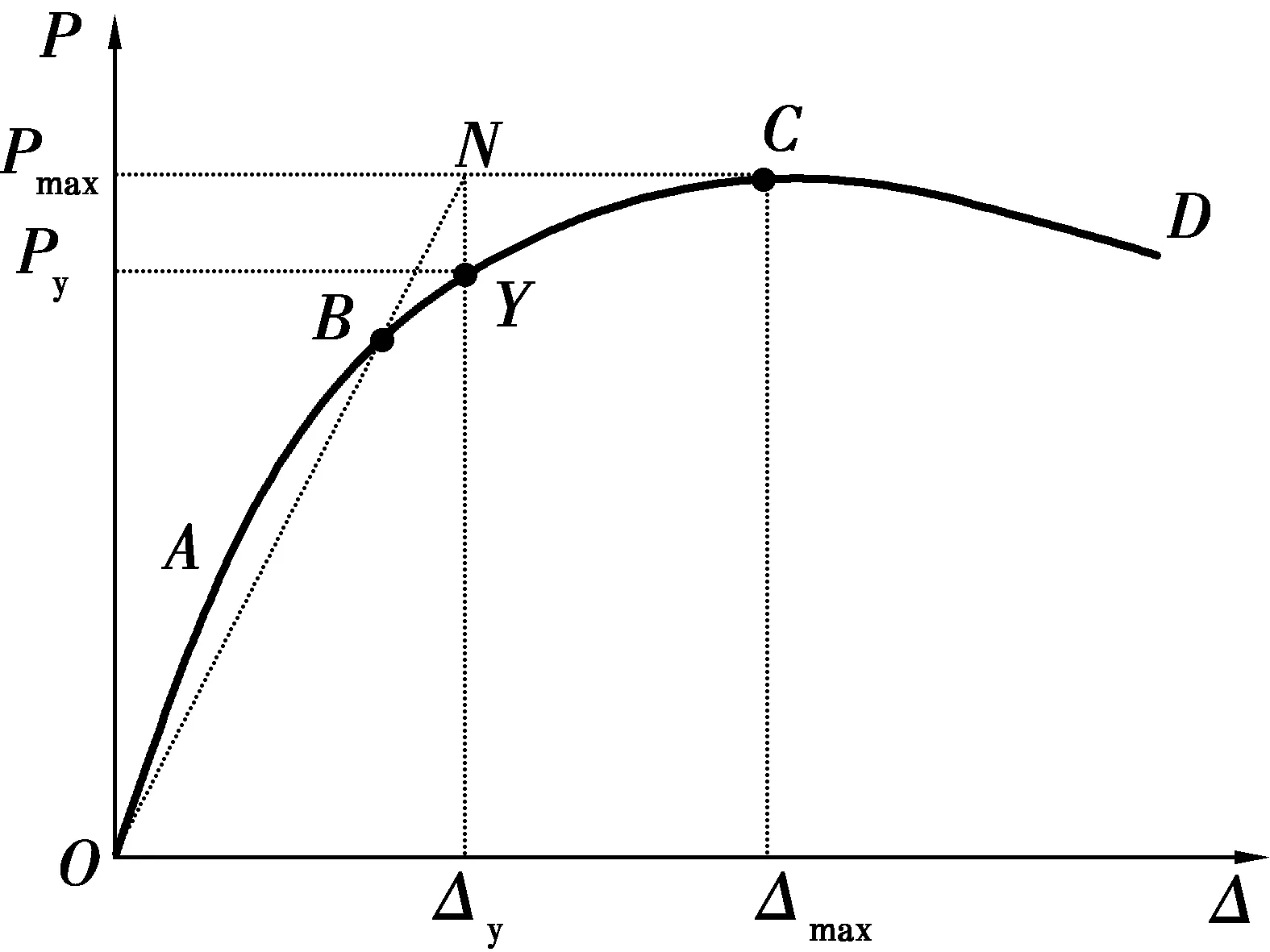
图6 屈服位移的确定Fig. 6 Definition of yield displacement of specimens
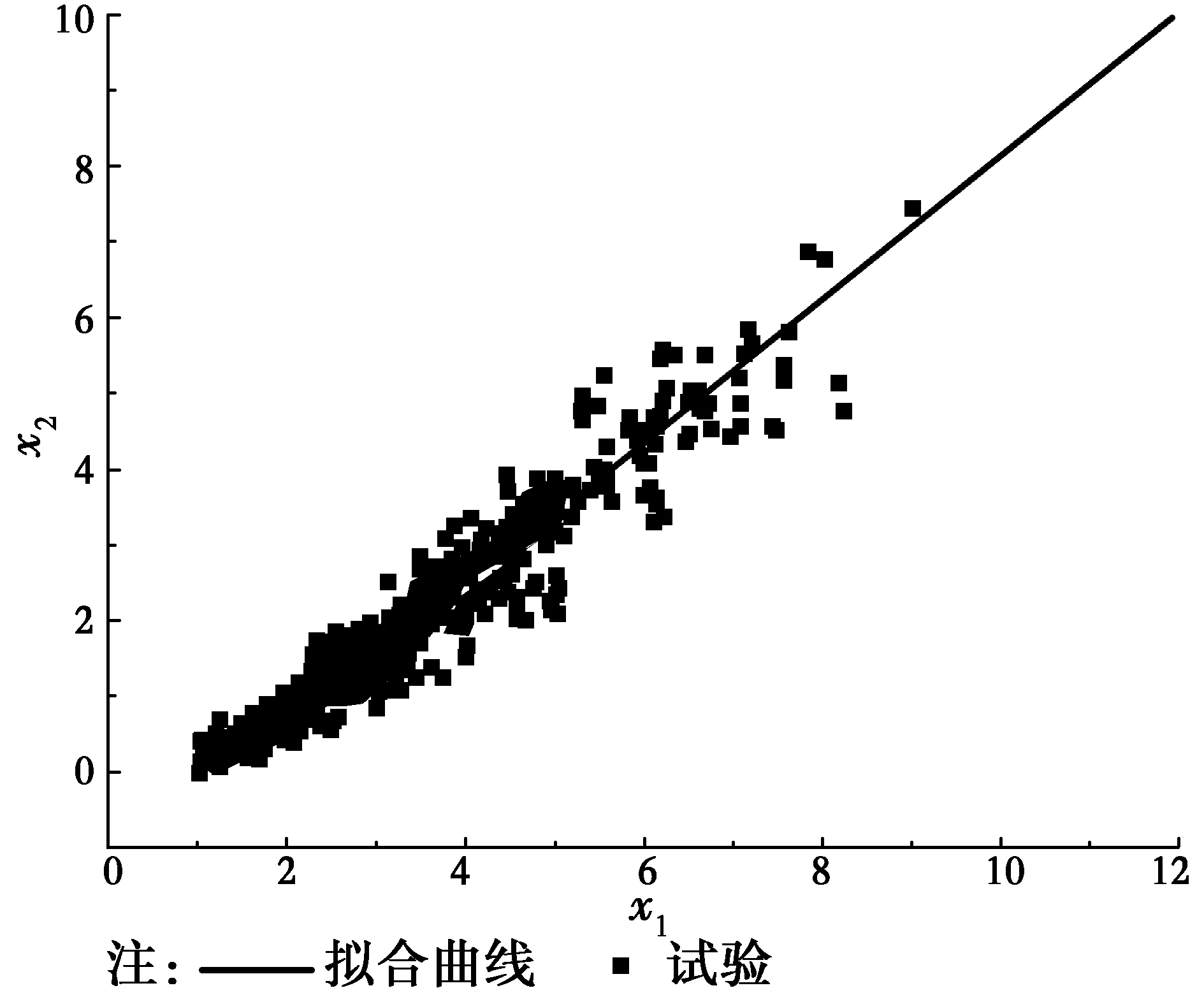
图7 滞回环上x2与x1的关系Fig. 7 Relationship between x2 and x1 in one hysteretic loop
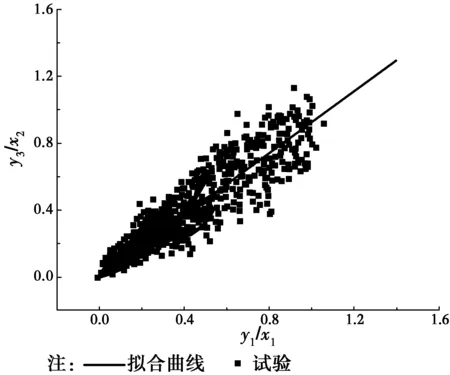
图8 滞回环上y3/x2与y1/x1的关系Fig. 8 Relationship between y3/x2 and y1/x1 in one hysteretic loop
y3/x2和y1/x1分别为图5(b)中直线OA和BC的斜率,式(2)中2个拟合参数分别为0.928和0.975,说明直线OA与BC近似平行[24]。
1.2 滞回环模型
根据弯曲破坏圆形截面偏心受压构件滞回环的特点,采用式(3)描述图5(b)所示滞回环的下半环。
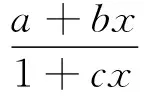
(3)
式中:a、b和c为待定系数。
利用如下3个条件:1)x=x1,y=y1;2)x=x2,y=0;3)x=-x1,y=-y1得到
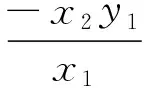
(4)
将式(4)代入式(3),得到过A、B和D三点的滞回环下半环的表达式
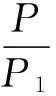
(5)
在式(5)中,取x=0,得到图5(b)中滞回环下半环与y轴的交点C的纵坐标值,即y3=-x2y1/x1。通过计算可以得出点B(x2,0)与点C(0,-x2y1/x1)连线的斜率为y1/x1,该值恰好等于点O(0,0)与点A(x1,y1)连线的斜率,说明采用式(5)表示滞回
环的下半环时,直线OA与BC是近似平行的,这与图8圆形截面试件滞回曲线上特征点的分析结果是一致的。因此,式(5)表示的数学表达式合理描述了试件滞回曲线的下半环。
考虑滞回环的反对称性,一个完整的滞回环曲线可用式(6)描述。
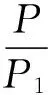
(6)
图9所示为式(6)的计算结果与试验所得荷载-位移(P-Δ)滞回曲线的比较,图中,计算滞回环的(x1,y1)是根据试验结果的骨架曲线确定的。并可以看出,根据式(6)计算得到的滞回曲线与试验滞回曲线非常接近。点(Δ1,P1)在滞回曲线的骨架曲线,分析实际的结构构件时,骨架曲线可以采用纤维法比较准确地确定,Δ2可根据式(1)确定。因此,只要根据构件的材料性能、截面尺寸和配筋计算得到构件滞回曲线的骨架曲线,即可由式(6)得到构件不同位移下的滞回曲线。

图9 模型计算的滞回环与试验滞回环的比较Fig. 9 Comparison of hysteretic loops between the predicted and the experiment
2 等效阻尼比
等效阻尼比ζeff为结构的粘滞阻尼比ζvis与等效滞回阻尼比ζhys之和。对于钢筋混凝土结构,ζvis取为0.05,ζhys按照结构的一个完整非线性滞回环消耗的能量与等效线性结构的一个循环粘滞阻尼消耗的能量相等确定(图5(b))。
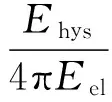
(7)
式中:Ehys为一个完整加载循环的耗能,即图5(b)中的阴影部分面积S(B′AB+BDB′);Eel为等效线性结构(构件)在一个加载循环中对应于最大位移的弹性变形能,即图5(b)中三角形OAF的面积S(OAF)或者三角形ODG的面积S(ODG)。
根据式(6)求得:
(8)
根据图5(b),Eel=S(OAF)=S(ODG)=x1y1/2。由式(7)得到
(9)
定义γ=x2,根据式(1)可以得出γ=0.765(μ-1)1.074,则式(9)可以表示为
(10)
图10为按式(10)、Rosenblueth等[9]和Kowalsky[10]所提模型计算的等效阻尼比随延性系数μ的变化,α为双线性荷载-位移曲线中屈服后刚度与初始刚度的比值。由图10可以看出,按Rosenblueth等[9]所提模型计算的等效阻尼比明显低于试验得到的等效阻尼比,按Kowalsky[10]所提模型计算的等效阻尼比明显高于试验得到的等效阻尼比,按本文模型计算得到的等效阻尼比与试验结果则比较接近。
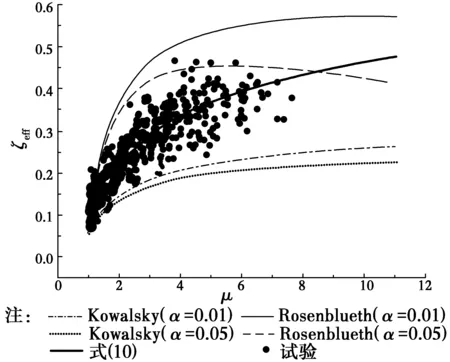
图10 计算与试验ξeff-μ关系曲线的比较Fig.10 Comparison of ξeff-μ relationship between the predicted and the experiment
图11为按不同公式计算的等效阻尼比ζeff,c与试验50根试件阻尼比ζeff,t的对比结果。从图中可以看出,根据Rosenblueth等[9]所提模型算得的等效阻尼比基本上都位于45度线之上,表明该模型高估了实际的等效阻尼比;相反,按照Kowalsky[10]所提模型算得的结果位于45度线之下,表明该模型低估了实际阻尼比;而采用本文所提模型算得的结果位于45度线附近,表明本文所提出的公式更为合理。

图11 计算阻尼比与试验阻尼比的比较Fig. 11 Comparison of equivalent damping ratios between the predicted and that obtained based on experimental results
3 双墩柱桥梁的整体结构等效阻尼比
以图12(a)所示双柱墩钢筋混凝土简支梁桥为例,说明建立结构整体等效阻尼比与构件塑性铰阻尼比关系的方法。
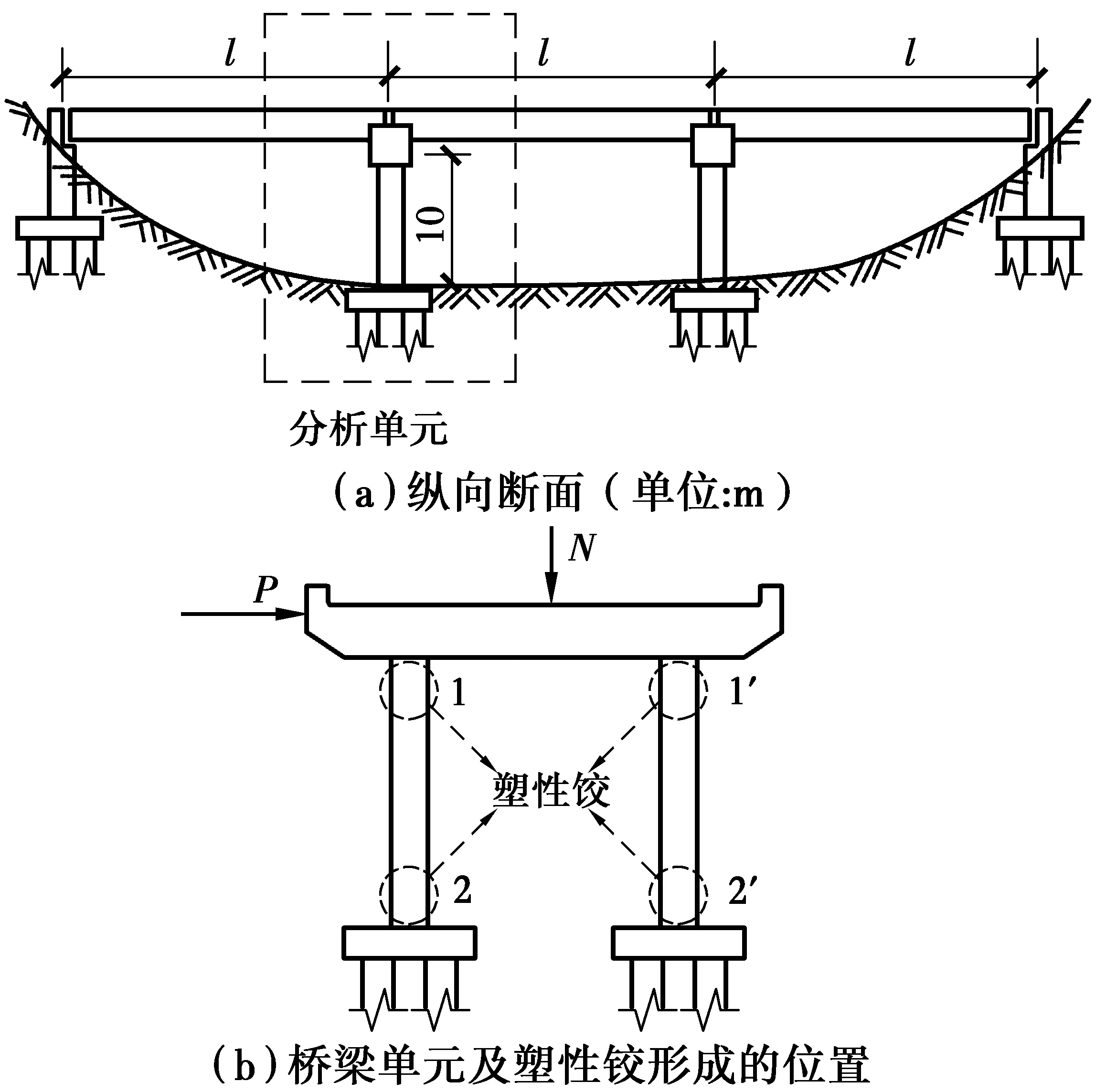
图12 双柱墩钢筋混凝土简支梁桥Fig.12 Two column piers supported bridge
用于分析的桥梁单元及分析单元上塑性铰区域如图12(b)所示。盖梁上作用有竖向力N和水平力P。假定墩柱的底部及顶部分别固定在底座和盖梁上,且底座及盖梁的强度、刚度均大于墩柱,则作用在盖梁上的侧向力P会均分到两个墩柱上,单个墩柱上侧向力为P/2。随着侧向力的增加,墩柱上会出现双曲率弯曲,反弯点距离顶部、底部的距离分别为l1和l2,如图13(a)所示。
通过截面分析可以确定墩柱顶部(i=1)及底部(i=2)的曲率φi,进而求得墩柱底部及顶部相对于反弯点的侧移[25]
(11)
式中
lpi=0.08li+0.022fyidi
(12)
式中:φyi为墩柱顶部(i= 1)和底部(i= 2)塑性铰的屈服曲率;Δyi和Δpi为墩柱顶部(i= 1)和底部(i= 2)的屈服位移及屈服后位移;lpi为塑性铰区长度;fyi和di分别钢筋的屈服强度及直径。
根据式(11)求得墩柱顶部及底部的侧向荷载-位移曲线如图13(b)~(d)所示。假定图12(b)所示的双柱墩中两墩柱底部纵向的配筋率大于顶部,塑性铰首先在顶部形成,随着荷载的增加,墩柱底部的塑性铰形成,该双柱墩的总侧向位移为
Δc=Δc1+Δc2
(13)
根据式(13)可以求得荷载从0增大至P/2,或从0反向加载至-P/2时,双柱墩的单调荷载位移曲线荷载,如图13(d)中的OAt和ODt。
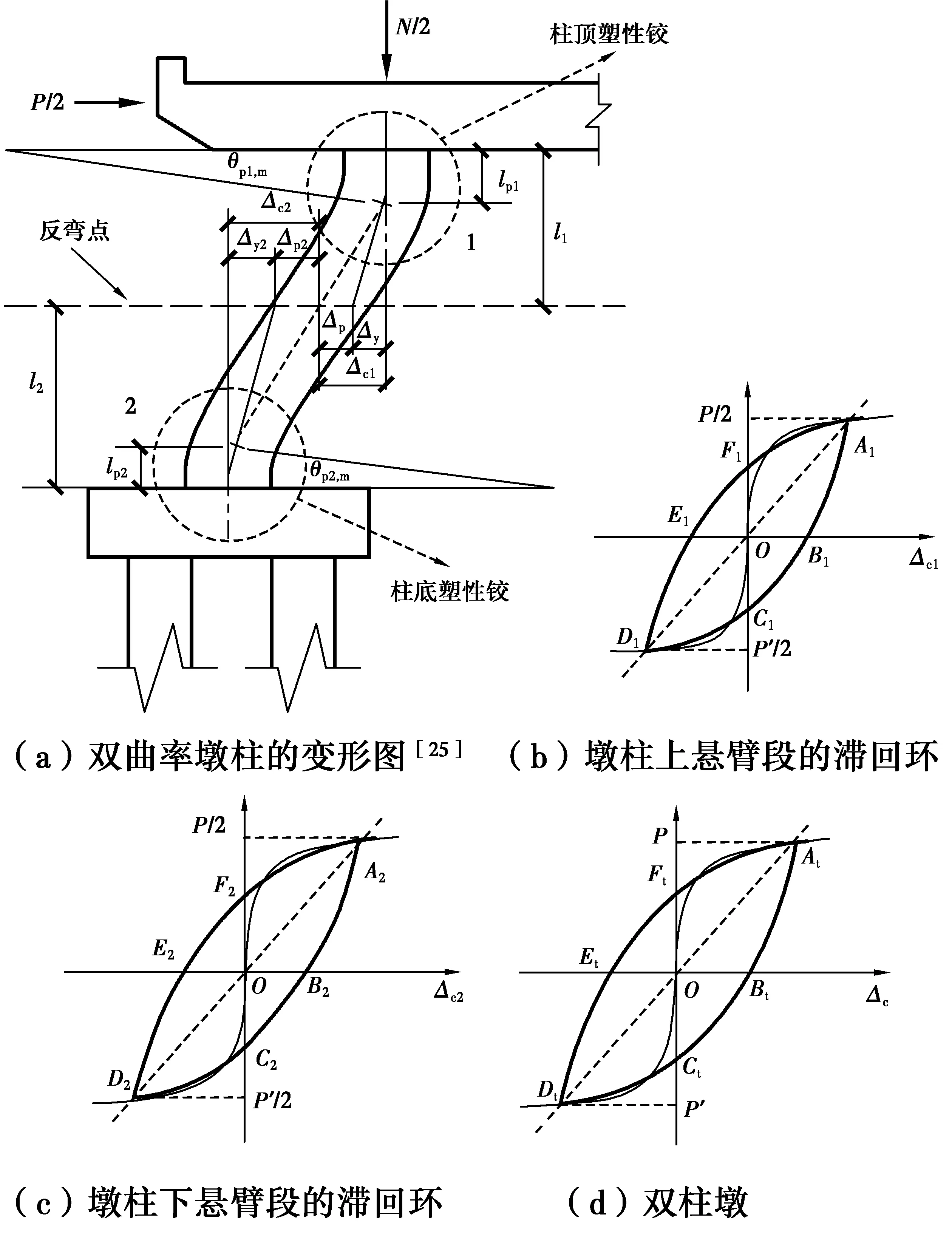
图13 墩柱变形图及墩柱的滞回环Fig.13 Relationships of displacement capacity and energy dissipation between the bridge and the potential plastic hinges of its columns
当盖梁上的加载路径为P→0→P′→0→P时,可以得到图13(d)所示双柱墩的循环荷载位移曲线AtBtCtDtEtFtAt。同时,可以得到墩柱顶部及底部塑性铰上,加载路径为P/2→0→P′/2→0→P/2时的循环荷载位移曲线A1B1C1D1E1F1A1和A2B2C2D2E2F2A2,如图13(b)及图13(c)所示。由于圆形截面钢筋混凝土构件中纵筋沿截面边缘均匀布置,所以,P和P′值相差不多,故可以假定曲线A1B1C1D1E1F1A1、A2B2C2D2E2F2A2以及AtBtCtDtEtFtAt为关于坐标系原点对称的封闭滞回环,与试验中各钢筋混凝土试件加载情况相符。
双柱墩的耗能能力等于两个墩柱的耗能能力之和,因此,图13(d)中环AtBtCtDtEtFtAt所消耗的能量为图13(b)中环A1B1C1D1E1F1A1与图13(c)中环A2B2C2D2E2F2A2所消耗能量的两倍(共有4个塑性铰)。根据式(7),墩柱上一个塑性铰耗散的能量为
Ehys,i=4πζhys,iEel,i=
(14)
式中:ζhys,i为墩顶(i=1)或墩底(i=2)的等效阻尼比,可根据式(10)计算。
(15)
因此,由式(14)和式(15)求得用墩柱上各塑性铰等效阻尼比表示的双柱墩耗能为
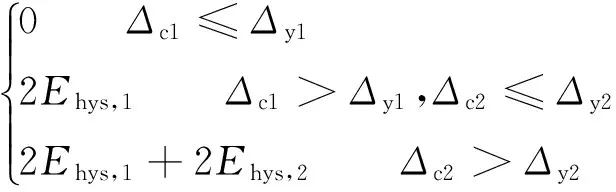
(16)
根据式(7),双柱墩的等效阻尼比为:
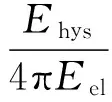
(17)
将式(16)代入式(17)并考虑弹性粘滞阻尼比,可以得到图12(b)所示双柱墩的等效阻尼比:
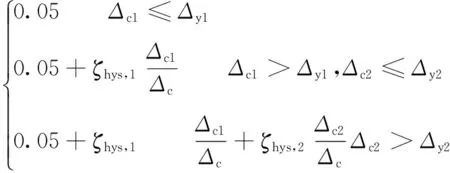
(18)
4 算 例
对图12所示双柱墩进行Pushover分析。桥墩高10m,上部集中质量为4.0×105kg,墩柱直径为1 000mm,墩柱顶部和底部配筋如图14所示,纵筋屈服强度和极限强度分别为410.4MPa和615.6MPa,箍筋屈服强度为410.4MPa,间距为100mm,混凝土强度为34.5MPa,保护层厚度为30mm。
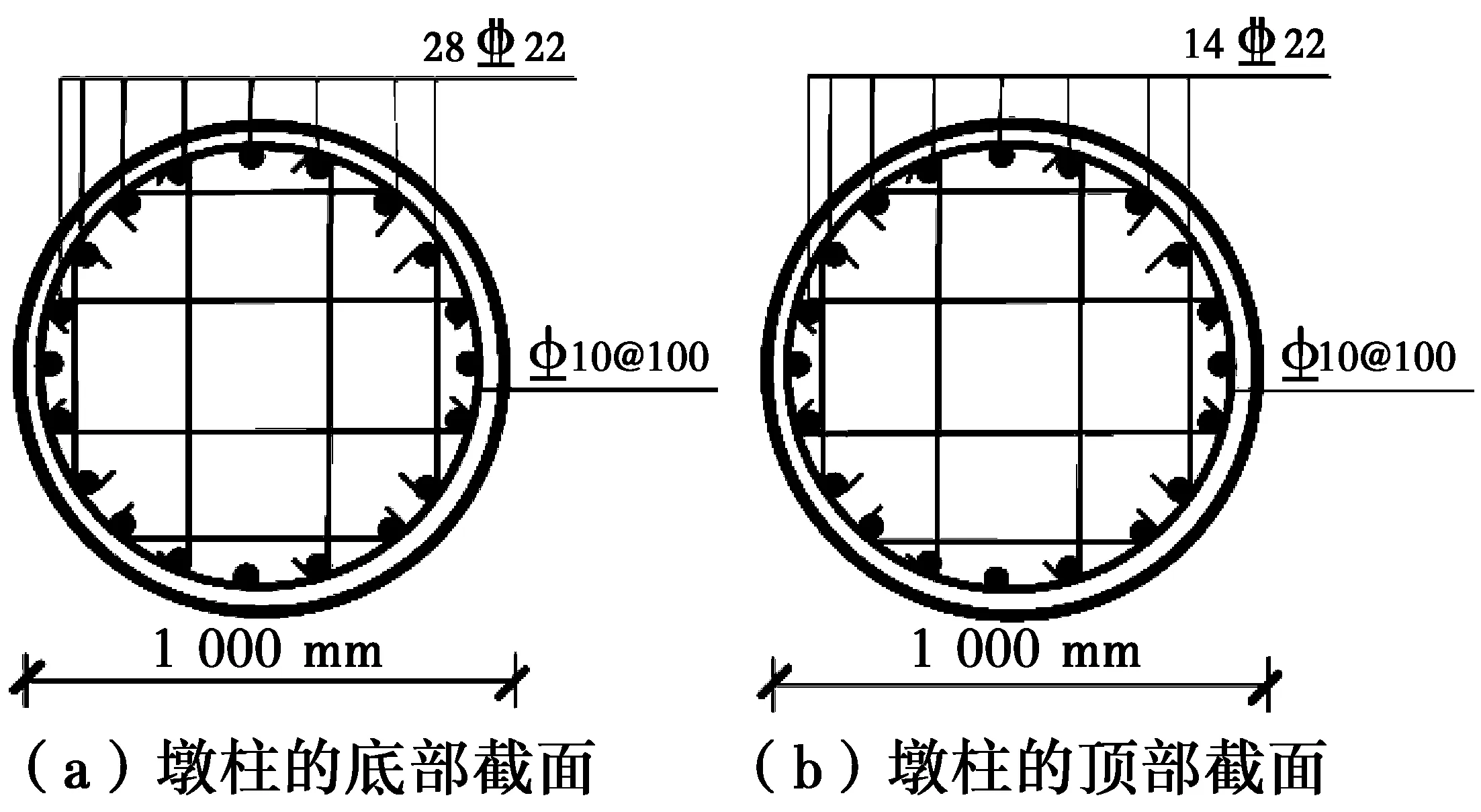
图14 墩柱顶部及底部横截面的配筋Fig. 14 Cross section and reinforcement details of bridge columns
钢筋应力-应变关系采用Esmaeily等[26]的三线段强化模型,保护层混凝土和核心混凝土分别采用Mander等[27]的应力-应变模型。通过截面分析求得单根墩柱上部、下部悬臂段的水平荷载-位移(相对于反弯点)曲线及整个柱墩的水平荷载-位移(墩顶相对于墩底)曲线,如图15所示。采用图6所示的方法得到曲线的等效屈服位移和屈服荷载也示于图15。
采用《公路桥梁抗震设计细则》[28]的反应谱进行Pushover分析。反应谱的形式为

(19)
式中:T为结构的周期;Tg为特征周期,本例取为0.45s;Smax为水平加速度反应谱最大值,按式(20)计算。
Smax=2.25CiCsCdA
(20)
式中:Ci为抗震重要性系数,抗震设防类别为C类时,取为1.0;Cs为场地系数,场地类别为Ⅱ类、峰值地面加速为0.4g时,取为1.0;A为水平向设计基本地震加速度,取为0.4g;Cd为阻尼调整系数,按式(21)计算。
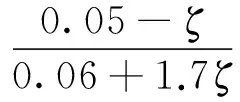
(21)
采用本文所的等效阻尼比模型,根据式(18)求出该双柱墩的性能点D及等效阻尼比如图16所示。为方便对比,也直接采用了Rosenblueth等[9]所提模型及Kowalsky[10]所提模型进行了计算。
由图16可以看出,采用本文模型算得的等效阻尼比为21.5%,目标位移为0.120 m;按照Rosenblueth[9]等所提模型以及Kowalsky[10]所提模型算得的等效阻尼比分别为25.52%和13.48%,目标位移分别为0.110 m和0.158 m。按本文模型算得的结果介于采用Rosenblueth等[9]所提模型和Kowalsky[10]所提模型算得的结果之间。
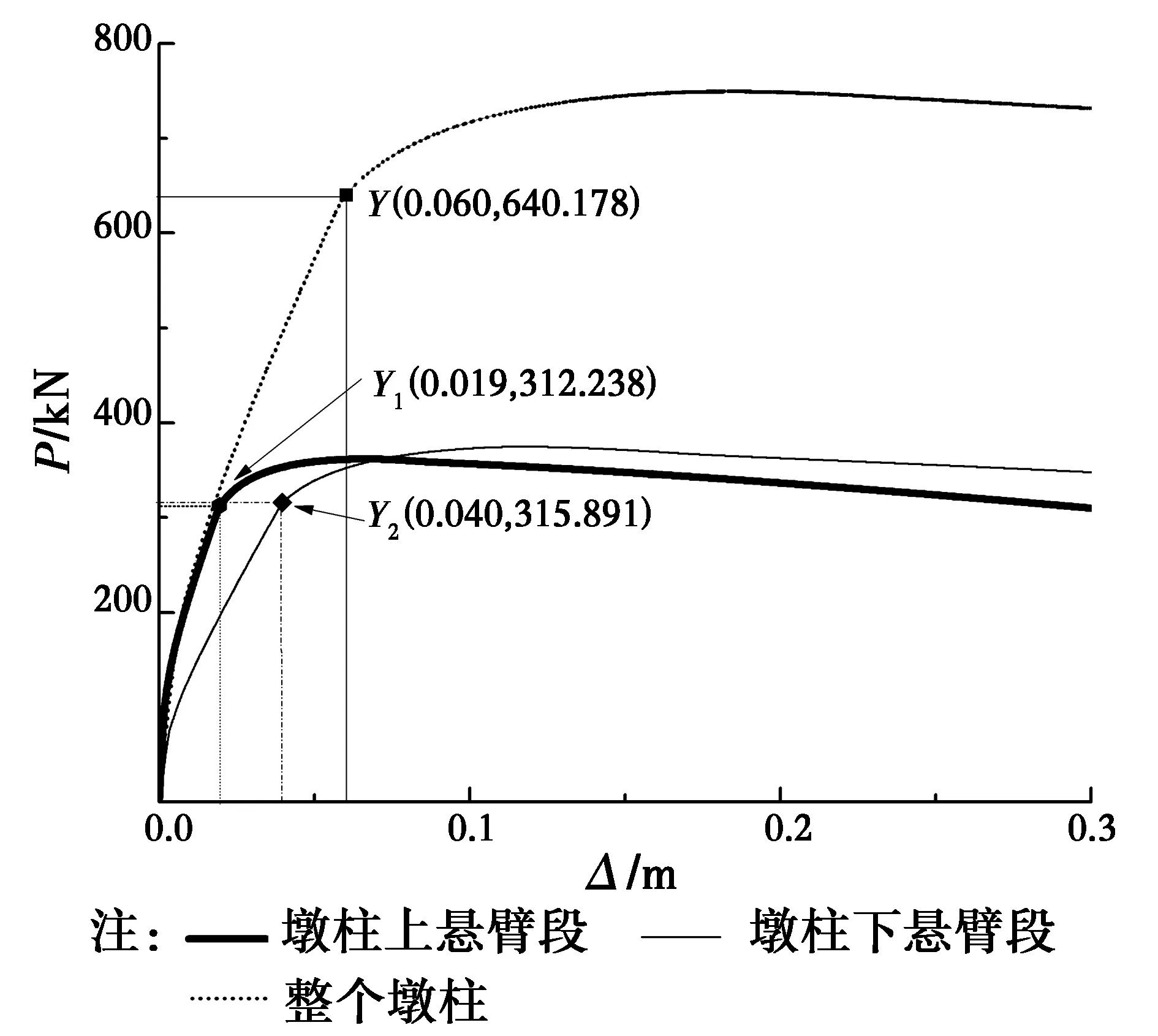
图15 荷载-位移曲线Fig.15 Lateral load-displacement curves

图16 基于不同等效阻尼比模型的目标位移及性能点Fig. 16 Performance points and target displacement in ADRS domain
5 结 论
根据弯曲破坏型钢筋混凝土圆柱的试验结果,建立了完整滞回环的数学模型,基于所建立的滞回环模型,根据Jacobsen理论推导得出圆柱的等效阻尼比模型。以双墩钢筋混凝土连续梁桥为例,建立了桥梁结构体系等效阻尼比与墩柱端部塑性铰等效阻尼比的转换关系式。本研究主要结论如下:
1)所提出弯曲破坏型钢筋混凝土圆柱的滞回环表达式较好地反映了弯曲破坏型试件的滞回特性;基于该模型建立的等效阻尼比模型概念明确,与试验结果吻合良好,可用于地震作用下弯曲破坏钢筋混凝土圆形截面偏心受压构件的抗震分析。
2)从原理上讲,用反映桥梁墩柱不同位置塑性铰及考虑塑性铰不同出现次序和转动情况的桥梁整体等效阻尼比分析地震作用下桥梁的位移,比目前Pushover分析中常用的采用一个构件的等效阻尼比计算桥梁的位移更能反映桥梁整体的耗能和等效粘滞阻尼特性。
3)以建立的单个塑性铰的等效阻尼比为基础、采用本文提出的桥梁整体等效阻尼比公式进行poshover分析,计算的桥梁目标位移与基于Rosenblueth模型以及Kowalsky模型的计算结果存在较大的差距。
[1] Federal Emergency Management Agency. NEHRP guidelines for the seismic rehabilitation of buildings [R]. FEMA 356. Washington D C,2000.
[2] Priestley M J N,Kowalsky M J. Direct displacement- based seismic design of concrete buildings [J]. Bulletin of the New Zealand Society for Earthquake Engineering,2000,33(4): 421-444.
[3] Chopra A K,Goel R K. Capacity-demand-diagram methods based on inelastic design spectrum [J]. Earthquake Spectra,1999,15(4): 637-656.
[4] Fajfar P,Fischinger M. N2-A method for non-linear seismic analysis of regular buildings[C]//Proceedings of the Ninth World Conference in Earthquake Engineering,1988,5: 111-116.
[5] Gasp P,Fajfar P,Fischinger M. An approximate method for seismic damage analysis of buildings[C]// Proceedings of the Tenth World Conference on Earthquake Engineering (Madrid), Rotterdam: AA Balkema,1992: 3921-6.
[6] Prestandard F E M A. Commentary for the seismic rehabilitation of buildings[R]. Rep. No. FEMA 356,2000.
[7] Jacobsen L S. Steady forced vibrations as influenced by damping [J]. Transactions ASME,1930,52:169-181.
[8] Jacobsen L S. Damping in composite structures[C]//Proceedings of 2nd World Conference on Earthquake Engineering,1960: 1029-1044.
[9] Rosenblueth E,Herrera1.On a kind of hysteretic damping [J]. Journal of Engineering Mechanics Division,ASCE,1964,90(l): 37-4.
[10] Kowalsky M J. Displacement-based design: A methodology for seismic design applied to RC bridge columns [D]. University of California at San Diego,La Jolla,California,1994.
[11] Takeda T,Sozen M A,Neilsen N N. Reinforced concrete response to simulated earthquakes [J]. Journal of the Structural Division,ASCE,1981,107(9):1713-1729.
[12] GuIkan P,Sozen M. Inelastic response of reinforced concrete structures to earthquake motions [J]. ACI Structural Journal,1974,71(12):604-610.
[13] Iwan W D. Estimating inelastic response spectra from elastic spectra [J]. Earthquake Engineering and Structural Dynamics,1982,8: 375 -388.
[14] Kwan W P,Billington S L. Influence of hysteretic behavior on equivalent period and damping of structural systems [J]. Journal of Structural Engineering,2003,129(5): 576 -585.
[15] 丁建国. 弹塑性反应谱及其在抗震设计中的应用[J]. 南京理工大学学报,2007,31 (6): 780- 783. Ding J G.Elasto-plastic response spectrum and its applications in a seismic design [J]. Journal of Nanjing University of Science and Technology,2007,31 (6): 780-783. (in Chinese)
[16] 曲哲,叶列平. 建筑结构弹塑性地震响应计算的等价线性化法研究[J]. 建筑结构学报,2010,31( 9) : 95-102. Qu Z,Ye L P.Equivalent linear analysis in estimating nonlinear seismic responses of building structures [J]. Journal of Building Structures,2010,31(9): 95-102. (in Chinese)
[17] 梁仁杰,吴京,孟少平. 能力谱法中等效阻尼比的误差分析及假设检验[J]. 土木工程学报,2010,43: 33 -36. Liang R J,Wu J,Meng S P.Error analysis and assumption test on the equivalent damping ratio in capacity spectrum method [J]. China Civil Engineering Journal,2010,43: 33 -36. (in Chinese)
[18] 程光煜 叶列平. 基于等效线性化方法弹塑性SDOF系统能量谱的研究[J]. 建筑结构,2007:37(8): 74-77. Cheng G Y,Ye L P.Estimation of input energy spectra of inelastic SDOF systems with equivalent linear method [J]. Building Structure,2007,37(8): 74-77. (in Chinese)
[19] 李妍,吴斌,欧进萍. 弹塑性结构等效线性化方法的对比研究[J]. 工程抗震与加固改造,2005,27(1): 1-6. Li Y,Wu B,Ou J P.Comparison of equivalent linearization methods for inelastic structures [J]. Earthquake Resistant Engineering and Retrofitting,2005,27(1): 1-6. (in Chinese)
[20] 马恺泽,鄢红良,刘伯权,等. 基于位移的抗震设计方法中的等效阻尼模型的研究[J]. 地震工程与工程振动,2013,33 (4): 134-139. Ma Z K,Yan H L,Liu B Q,et al. Research on equivalent damping ratio for displacement-based seismic design method [J]. Journal of Earthquake Engineering and Engineering Vibration,2013,33 (4): 134-139. (in Chinese)
[21] 陆本燕,刘伯权,刘鸣,等. 等效阻尼比对基于位移的抗震设计的影响分析[J]. 防灾减灾工程学报,2010,30(6): 667- 673. Lu B Y,Liu B Q,Liu M,et al.Analysis of equivalent damping ratio on displacement-based seismic design [J]. Journal of Disaster Prevention and Mitigation Engineering,2010,30(6): 667- 673. (in Chinese)
[22] 贡金鑫. 钢筋混凝土构件等效阻尼比研究[R]. 大连理工大学,2013. Gong J X.Research on equivalent damping ratio of reinforced concrete elements [R]. Dalian University of Technology,2013. (in Chinese)
[23]Pacific Earthquake Engineering Research Center. PEER structural performance database[DB].http://www.ce.washington.edu/~peera1/,University of California,Berkeley,2004.
[24] 张勤,贡金鑫,姜凤娇,等. 钢筋混凝土柱非线性特性的分析方法[J]. 土木建筑与环境工程,2011,33 (6): 51-58. Zhang Q,Gong J X,Jiang F J,et al. Analysis method for nonlinear properties of reinforced concrete columns[J]. Journal of Civil,Architectural and Environmental Engineering,2011,33 (6): 51-58. (in Chinese)
[25] Caltrans Seismic Design Criteria[S]. California Department of Transportation,Sacramento,California,2010.
[26] Esmaeily G H,Xiao Y. Seismic behavior of bridge columns subjected to various loading patterns[R]. Pacific Earthquake Engineering Research Center. University of California,Berkeley,California,2002.
[27] Mander J B,Priestley M J N,Park R. Theoretical stress-strain model for confined concrete[J]. Journal Structure Engineering,ASCE,1988,114(8),1804-1826
[28] JTG/T B02—01—2008 公路桥梁抗震设计细则[S]. 北京: 人民交通出版社,2008 JTG/T B02—01—2008. Guidelines for seismic design of highway bridge [S]. Beijing: China Communications Press ,2008. (in Chinese)
(编辑 胡 玲)
Equivalent damping ratio of RC circular columns and its application in bridge seismic analysis
ZhangYanqing1,GongJinxin1,ZhangQin2,HanShi1
(1. Department of Civil Engineering,Dalian University of Technology,Dalian 116024,Liaoning,P.R. China;2.College of Civil and Transportation Engineering,Hohai University,Nanjing 210098,P.R. China)
Based on analysis of the test results of 50 RC specimens of circular columns failed in flexure,an expression for defining the hysteretic loop is proposed and a model for predicting the equivalent damping ratio is developed. The procedure for associating the equivalent damping ratio of a structure as a whole with those of its element is established by an example of double-column pier-bridge. It’s indicated that the expression of hysteretic loop proposed well defines the hysteretic loops of RC columns. Rational outcome can be expected when performing pushover analysis using the relationship of equivalent damping ratio of a bridge as a whole with those of its element. The target displacement predicted with the proposed model is different from those predicted with Rosenblueth’s model and Kowalsky’ model.
Reinforced concrete;circular columns;flexural failure;hysteretic loop;equivalent damping ratio.
10.11835/j.issn.1674-4764.2015.05.001
2015-03-03 基金项目:国家自然科学基金(51278081;51478077)
张艳青(1983-),女,博士生,主要从事结构工程研究,(E-mail)zhangyanqingtaian@163.com。 贡金鑫(通信作者),男,教授,博士生导师,(E-mail)jinxingong@163.com。
Foundation item:National Natural Science Foundation of China(No.51278081,51478077)
TU357.3
A
1674-4764(2015)05-0001-10
Received:2015-03-03
Author brief:Zhang Yanqing(1983-),PhD.main interest:seismic research of RC structure,(E-mail)zhangyanqingtaian@163.com. Gong Jinxin(corresponding author),professor,(E-mail)jinxingong@163.com.

