蠕变模型对约束钢梁抗火性能分析的影响

王卫永,何平召

(重庆大学 a.土木工程学院；b.山地城镇建设与新技术教育部重点试验室(重庆大学)，重庆 400045)

蠕变模型对约束钢梁抗火性能分析的影响

王卫永a,b,何平召a

(重庆大学 a.土木工程学院；b.山地城镇建设与新技术教育部重点试验室(重庆大学)，重庆 400045)

钢材在高温和荷载作用下产生明显蠕变变形，影响火灾中结构的变形和受力性能。现有的蠕变模型较多，但没有一个广泛适用的蠕变模型。不同的蠕变模型对钢结构抗火分析结果有很大影响。为了量化蠕变模型对约束钢梁抗火性能分析的影响，对5种常用的蠕变模型进行了对比分析。采用编写的约束钢梁计算程序，分别计算5种蠕变模型下约束钢梁的抗火性能并与试验数据进行对比。结果表明，采用Norton蠕变模型的计算结果与试验数据吻合最好。最后对影响约束钢梁抗火性能参数进行了研究，研究发现，Harmathy蠕变模型对约束梁抗火性能分析结果影响最大；不同蠕变模型对不同荷载比、约束刚度下的约束钢梁抗火性能影响程度均不同。

蠕变模型;约束钢梁;抗火性能;钢结构

在火灾作用下，钢材的高温蠕变会对钢结构的抗火性能产生很大影响。目前已经有多位学者开展了蠕变对钢梁抗火性能影响方面的研究，例如Skowronski[1]提出了一种考虑高温下钢材蠕变的新模型,并进行了火灾下钢梁的变形研究；Kodur等[2]采用ANSYS软件建立约束钢梁分析模型，发现考虑和不考虑蠕变对钢梁影响较大，忽略蠕变会低估钢梁的挠度，将导致结构不安全；Toric等[3]提出一个考虑高温钢材蠕变的数值模型，该模型通过修正静力下材料的应力-应变关系来考虑蠕变，用该数值模型模拟了3根简支梁，与试验结果吻合较好。Li等[4]建立了约束钢梁的分析方法，能较好地与试验数据吻合,但是未能考虑蠕变对约束钢梁抗火性能的影响。

钢材高温蠕变模型有很多,较早的有Dorn[5]蠕变模型，在Dorn蠕变基础上发展得到的Harmathy[6]蠕变模型，以及广泛应用的Fields[7]蠕变模型，通过对试验数据的拟合得到的Williams-Leir[8]模型，从黏弹性力学的概念出发得到的Burger’s[9]模型，还有形式简单的Norton蠕变模型等。各种蠕变模型考虑的蠕变阶段不尽相同，蠕变方程形式差异很大，得到的蠕变应变也具有明显的差异。蠕变模型参数的取值与蠕变试验所取的钢材种类也有一定的关系，造成现有的蠕变模型差异很大。为了研究不同蠕变模型对约束钢梁抗火性能分析的影响。采用文献[4]中考虑蠕变的约束钢梁分析方法，对采用不同蠕变模型的约束钢梁抗火性能分析结果进行比较，研究发现，Harmathy蠕变模型对约束梁火灾反应影响最大，不同荷载比、约束刚度下的蠕变影响程度不同。

1 蠕变模型介绍

钢材高温蠕变现象是指在高温和应力作用下，钢材产生的永久变形随时间而增长的现象。钢材在高温下的蠕变增量不仅与其所处的应力状态、温度有关，而且还受应力过程及升温过程的影响。恒温恒载条件下典型单轴蠕变曲线如图1所示[8]。在外力作用下，试件即产生瞬时应力和应变，瞬时应变包含弹性应变ɛe和与时间无关的塑形应变ɛp构成。随着时间的增长，钢材的蠕变应变ɛcr开始逐渐发展。大体上可以分为3个阶段：第1阶段(又称瞬时蠕变阶段，对应图1中AB段)为蠕变的初期阶段，应变增长速率随时间增长而减小；第2阶段(又称稳态蠕变阶段，对应图1中BC段)的应变速率大致保持恒定，蠕变速率最小；第3阶段(又称加速蠕变阶段，对应图1中CD段)的蠕变增长速率急剧增大，直至构件断裂。

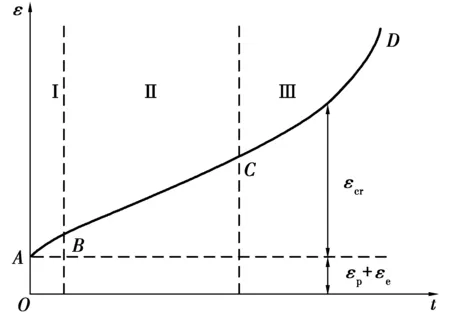
图1 蠕变随时间变化曲线示意图Fig.1 Schematic of creep-time curve

1.1 Harmathy蠕变模型

Harmathy是最早研究钢结构高温蠕变模型的研究者之一。Harmathy在Dorn理论基础上进行了修正，提出了可以对变应力下的蠕变应变进行计算的Harmathy模型[6]，该模型能考虑蠕变的前两个阶段。其核心是把温度和时间这两个变量合成一个变量——温度补偿时间θ来表示。Harmathy模型主要用于常应力下的计算，对变应力下的蠕变计算可能不够准确[10]。Harmathy给出了多个表达式[6]。其中一个常用的Harmathy蠕变模型的表达式为

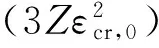
(1)

(2)

式中：Z、ΔH、ɛcr0是与材料有关的参数；R为气体常数；t为时间。

文献[6]给出了A36钢(屈服强度约248 MPa)的参数取值为

(3)

εcr,0=1.03×10-6σ1.75

(4)

ΔH/R=38 890

(5)

该组参数中应力σ的单位为MPa；时间t的单位为min；温度T的单位为℃。

1.2 Fields & Fields蠕变模型

Fields等[7]蠕变模型形式简单，不仅能表示蠕变的初始阶段，并且能较好地表示蠕变的稳态阶段，表达式为

εcr=atbσc

(6)

式中：a、b、c是与温度有关的参数，取值与钢材的材性有关。文献[7]给出A36钢的参数取值为

(7)

b=-1.1+0.003 5T

(8)

c=2.1+0.006 4T

(9)

该组参数中应力σ的单位为ksi(1 ksi=6.895 MPa)；时间t的单位为min；温度T的单位为℃。

1.3 Williams-Leir蠕变模型

研究中发现，在恒定应力和温度下，蠕变应变的对数lgεcr与时间的对数lgt大致成线性关系。Williams-Leir[8]利用该关系，通过对试验数据的分析提出了蠕变计算经验公式

(10)

式中：a1～a8是与钢材型号有关的参数。

Williams-Leir[8]给出了7种钢材的参数。对于常用的A149钢材(屈服强度245 MPa)，参数分别为：a1=-1.958×10-2；a2=9.528×10-2；a3=5.009×10-5；a4=-1.719×10-7；a5=-9.732×10-5；a6=-2.601×10-7；a7=1.43×10-7；a8=16.53。该组参数中应力σ的单位为psi(1 psi=6.895 kPa)；时间t的单位为min；温度T的单位为℃。

1.4 ANSYS Creep 11蠕变模型

有限元软件ANSYS提供了13种隐式蠕变模型，第11种蠕变模型是基于Zienkiewicz等[11]的塑性和蠕变应变统一理论提出的，该模型能准确模拟蠕变的前2个阶段，称为Creep11蠕变模型。其表达式如式(11)所示。Kodur等[2]根据SM50A钢(屈服强度约345 MPa)以及A36钢材(屈服强度约248 MPa)的高温蠕变试验数据，给出了参数c1～c7的值。该模型计算得到的蠕变应变与常应力和变应力下的试验数据吻合都较好。

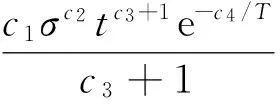
(11)

式中：c1=6×10-6；c2=6.95；c3=-0.4；c4=16 500；c5=6×10-6；c6=6×10-5；c7=5×10-3。

该组参数中应力σ的单位为MPa；时间t的单位为min；温度T的单位为℃。

1.5 ANSYS Norton蠕变模型

ANSYS第10种蠕变模型为Norton蠕变模型，该模型只考虑蠕变的第2个阶段，方程中仅有3个参数，蠕变速率与时间无关。该蠕变模型其实是Creep11模型的一部分，即蠕变的第2阶段。闫守海[12]对Q345和Q460两种钢材进行了大量的蠕变试验，利用Norton蠕变模型进行了参数拟合，得到了d1到d3的值(称为Norton蠕变模型)。其蠕变速率表达式为

(12)

对于Q345钢材，式中：d1=4.090 2×10-17；d2=2.1；d3=10 660。该组参数中应力σ的单位为Pa；时间t的单位为s；温度T的单位为K。

2 蠕变模型对比

为了对比上文介绍的蠕变模型的差异，分别计算了不同温度下，蠕变应变达到2%需要的时间。以及不同应力下，蠕变应变达到2%需要的时间。在应力为100 MPa下蠕变应变达到2%需要的时间t与所处温度T的关系如图2(a)所示。纵坐标对时间t取以10为底的对数。从图2(a)中可以看出，不同蠕变模型的差异较大，在温度低于600 ℃时，Norton模型在蠕变应变达到2%需要的时间最短，即在相同时间下，Norton蠕变模型的蠕变应变最大。当温度大于630 ℃时，Norton模型达到2%需要的时间最长，即在相同时间的蠕变应变最小。总体上，Harmathy蠕变模型、Fields等蠕变模型和Williams-Leir蠕变模型差异较小。在540～630 ℃之间，Creep11模型在蠕变应变达到2%需要的时间最长，即在相同时间的蠕变最小。除了Fields等和Creep11模型外，其他模型的高温温度与蠕变应变达到2%所需时间的对数都近似是直线关系。但在一定程度上，5种蠕变模型的高温温度与蠕变应变达到2%需要的时间的对数都近似是直线关系。

在温度为600 ℃时，蠕变应变达到2%需要的时间与应力的关系如图2(b)所示。从图2(b)中可以看出，5种模型的应力与蠕变应变达到2%需要的时间的对数均近似为直线关系。在应力小于110 MPa时，Creep11达到2%的蠕变应变需要的时间最长。即在相同时间的蠕变应变最小。Norton蠕变模型在温度(应力)较低的时候，相同条件下的蠕变应变最大，在温度(应力)较高的时候，相同条件下的蠕变应变最小。

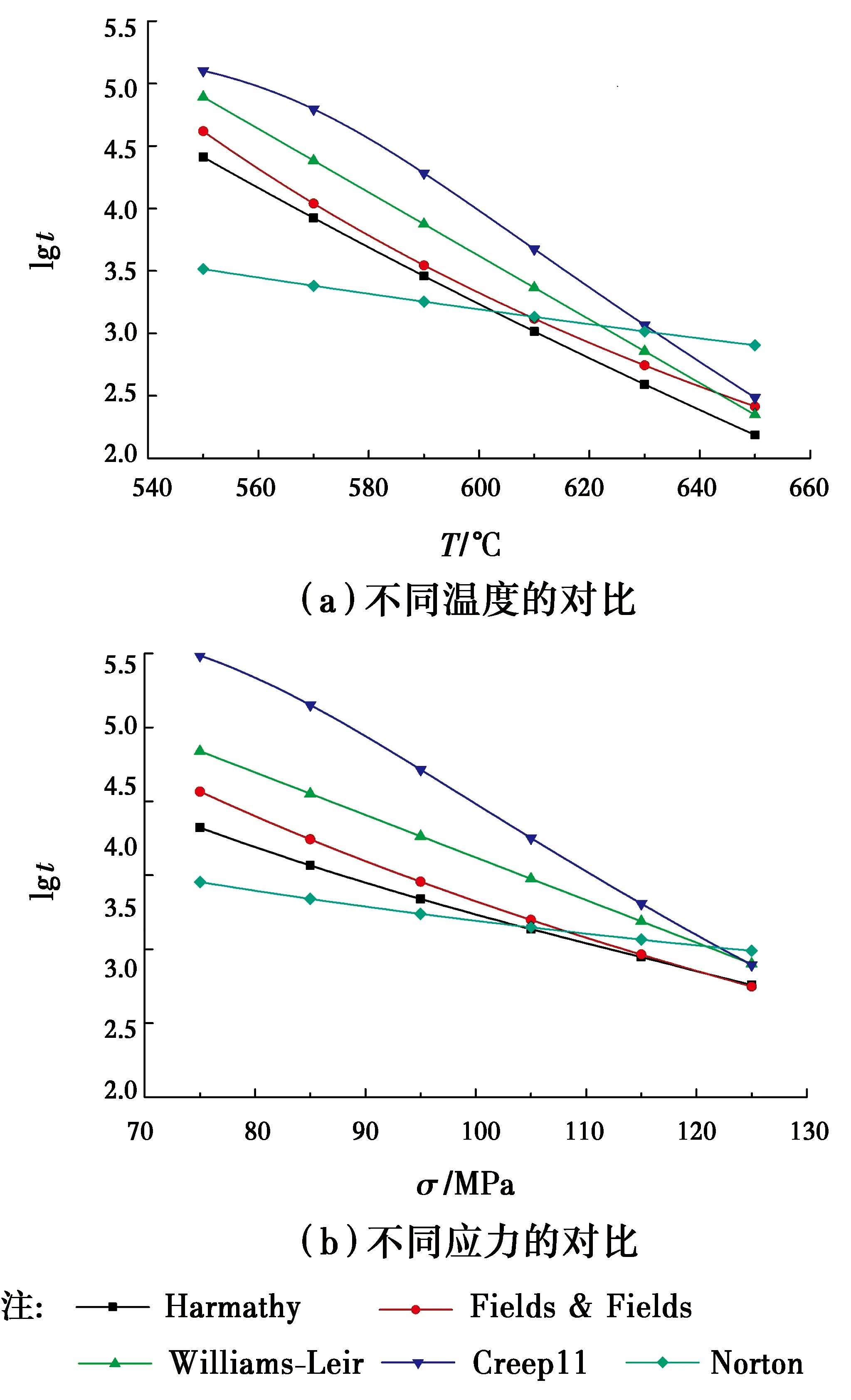
图2 蠕变模型的对比Fig.2 Comparison of creep models

3 模型试验对比

在文献[4]约束钢梁抗火分析方法的基础上，该方法引入蠕变模型和参数，通过对截面的力学应变进行修正，提出了一种考虑蠕变效应的约束钢梁分析方法。高温下的应力-应变关系采用Poh模型[13]。Liu等[14]完成了钢材型号为s275(屈服强度275 MPa)的约束钢梁抗火试验。上述5种蠕变模型的参数是根据不同的钢材的蠕变试验得到的。为了适应计算约束梁钢材的蠕变特性，文献[15]提出在计算蠕变时，对应力进行调整，应力的调整系数为该蠕变模型采用钢材的屈服强度与蠕变计算时的钢材屈服强度的比值。经过此应力调整，相同应力下，屈服强度越高的钢材，在相同条件下的蠕变应变越小；反之亦然。

Creep11蠕变模型的参数是Kodur等[2]根据SM50A钢(屈服强度约345 MPa)以及A36钢材(屈服强度约248 MPa)的高温蠕变试验数据得到的。其模型能较好地与这2种不同屈服强度的钢材的蠕变试验数据吻合。因此，在计算屈服强度介于这2种钢材之间的约束钢梁的蠕变应变时，不对其应力进行调整。

根据该分析方法，利用MATLAB编写计算程序。分别采用上述5种蠕变模型进行计算，与Liu[14]试件FUR13试验结果进行对比，试件FUR13的详细信息可参考文献[14]。与试件FUR13的对比结果如图3所示。从图3中可以看出，不考虑蠕变计算的挠度偏小，轴力偏大，考虑蠕变后挠度增大，轴力偏向于受拉。不同蠕变模型的影响程度不同。由图2(a)可知，Harmathy模型、Fields等模型和Williams-Leir模型在温度大于600 ℃以后的蠕变应变较大。采用Norton蠕变模型计算蠕变应变时，需要对应力进行调整，由于Norton蠕变模型参数是根据屈服强度为Q345钢材得到的，该约束钢梁的钢材为s275，故调整后，计算的蠕变应变增大。而Creep11蠕变模型没有调整，根据图2(a)和图2(b)，该蠕变模型的蠕变应变都比较小。所以，采用Creep11蠕变模型对该约束钢梁影响较小。

图3 采用不同蠕变模型分析结果与试验的对比Fig.3 Comparison between the results by different creep models and test data

Norton蠕变模型在温度较低时蠕变较大。从与试验数据的吻合来看，Norton蠕变模型与试验数据吻合最好。挠度达到l/20时的时间相差约30 s，误差仅为2.4%。最大轴向压力相差为2.3 kN，误差为3.6%，是5种蠕变模型计算结果中与试验数据吻合最好的。

4 蠕变模型的影响分析

为了进一步分析对选用不同蠕变模型对约束钢梁抗火性能计算结果的影响。设计了4个约束钢梁算例，约束钢梁截面为H400×200×8×13，跨度l为5 m，钢梁为Q345钢，屈服强度为345 MPa，高温下的应力-应变关系采用Poh模型[13]。作用均布荷载，空气温度均按ISO-834标准升温曲线控制，并考虑截面的不均匀温度分布,计算蠕变应变时考虑了应力调整。4个算例主要考虑不同的轴向约束刚度比(轴向约束刚度和钢梁抗拉刚度的比值)、不同的转动约束刚度比(转动约束刚度和钢梁抗弯刚度的比值)和不同的荷载比(为实际作用荷载与相同简支梁在常温下屈服荷载的比值)。其取值如表1所示。约束梁编号采用B序号-荷载比-轴向约束刚度比-转动约束刚度比的形式。

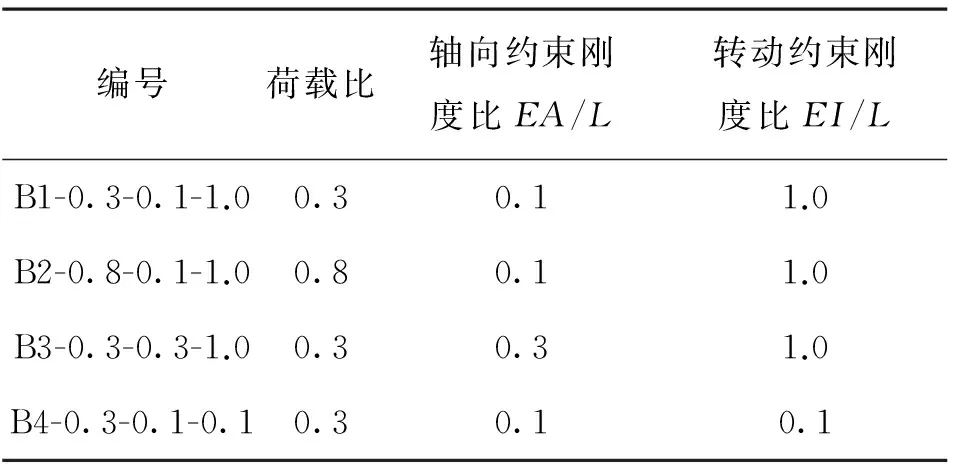
表1 参数取值信息Table1 Information of parameter selection

梁B1-0.3-0.1-1.0与其他3根梁的比较如图4～图6所示。分别比较挠度达到l/20=0.25 m经历的时间和达到的最大轴向压力。从图中可以看出，蠕变对约束钢梁抗火性能影响很大。对于4种不同的约束钢梁，总体上，与不考虑蠕变相比，Harmathy蠕变的影响最大。其他4种蠕变模型的对不同条件的约束梁影响不同。

图4是不同荷载比下的计算结果。荷载比为0.3的梁B1-0.3-0.1-1.0考虑与不考虑蠕变时的挠度达到l/20=0.25 m的时间最大相差为150 s。最大轴向压力相差约50 kN。从荷载比为0.8的梁B2-0.8-0.1-1.0可以看出，时间最大相差仅为40 s，最大轴向压力相差也仅为27 kN。小于荷载比为0.3时蠕变对其的影响。因此，荷载比越小，受火时间越长，能达到的临界温度越高，蠕变对约束钢梁结构反应影响也越大。

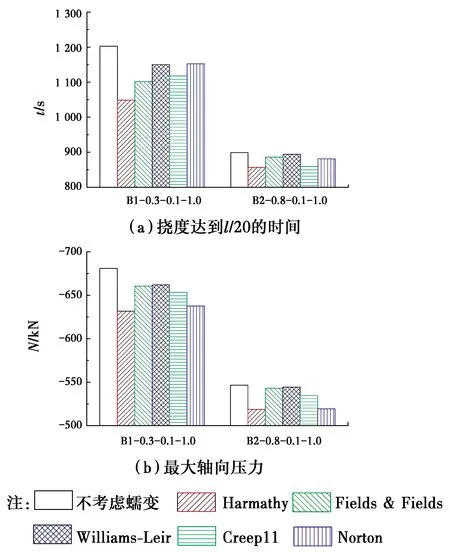
图4 不同荷载比下蠕变对约束梁抗火性能的影响Fig.4 Effect of creep on fire resistance of restrained beams subjected to different load ratio

图5是不同轴向约束刚度下的计算结果。梁B3-0.3-0.3-1.0中考虑与不考虑蠕变挠度达到0.25 m的时间最大相差仅为60 s。最大轴向压力相差25 kN。小于梁B1-0.3-0.1-1.0的计算值，说明轴向约束刚度越大，蠕变对结构反应影响越小。轴向约束刚度越大，梁越早进入屈服，但此时温度不高，蠕变影响较小。随后轴力较小，应力减小，蠕变应变也较小。

图6是不同转动约束刚度下的计算结果。梁B4-0.3-0.1-0.1中考虑与不考虑蠕变挠度达到0.25 m的时间最大相差为200 s，最大轴向压力相差72 kN，大于梁B1-0.3-0.1-1.0的计算值，转动约束刚度越小，蠕变对结构反应影响越大，转动约束刚度越大，蠕变对结构反应影响越小。转动约束越大，梁跨中应力越小，产生的蠕变应变就越小，所以蠕变对抗火性能影响越小。

图5 不同轴向约束下蠕变对约束梁抗火性能影响Fig.5 Effect of creep on fire resistance of restrained beams subjected to different axial restraints

5 结 论

通过对蠕变模型的对比和采用不同的蠕变模型对约束钢梁进行抗火性能分析，得到以下结论：

1)温度高于600 ℃时，Harmathy蠕变模型、Fields 等蠕变模型和Williams-Leir蠕变模型的蠕变应变较大，Creep11模型蠕变较小。

2)温度低于600 ℃时，Norton蠕变模型的蠕变应变比其他蠕变模型大，但此温度下的蠕变应变很小。在温度高于600 ℃时，Norton蠕变模型的蠕变应变最小。

3)计算蠕变应变时，对应力调整后，与不考虑蠕变相比，采用Harmathy蠕变模型对约束钢梁抗火分析结果影响最大。

4)荷载比和约束刚度越大的钢梁，蠕变的影响越小。

[1] Skowronski W. A study of the steel beam deformation during fire [J]. Building and Environment,1988,23(2):159-167.

[2] Kodur V K R,Dwaikat M M S. Effect of high temperature creep on the fire response of restrained steel beams [J].Materials and Structures,2010,63:1327-1341.

[3] Toric N,Harapin A,Boko I. Experimental verification of a newly developed implicit creep model for steel structures exposed to fire [J]. Engineering Structures,2013,57:116-124.

[4] Li G Q,Guo S X.Analysis of restrained steel beams subjected to heating and cooling part 1: Theory[J]. Steel and Composite Structures,2008,8(1):1-18.

[5] Dorn J E. Some fundamental experiments on high temperature creep [J]. Journal of the Mechanics and Physics of Solids,1955,3 (2): 85-116.

[6] Harmathy T Z. A comprehensive creep model [J]. Journal of Basic Engineering,1967,89 (3): 496-502.

[7] Fields B A,Fields R J. Elevated temperature deformation of structural steel [R]. Gaithersburg,MD: National Institute of Standards and Technology,1989.

[8] Willams-Leir G. Creep of structural steel in fire: analytical expressions [J]. Fire and Materials,1983,7 (2): 73-78.

[9] Findley W N,Lai J S,Onaran K. Creep and relaxation of nonlinear viscoelastic material [M]. New York: Dover Publication,1989.

[10] Tan K H,Ting S K,Huang Z F. Visco-elasto-plastic analysis of steel frames in fire [J]. Journal of Structural Engineering,2002,128 (1): 105-114.

[11] Zienkiewicz O C,Cormeau I C. Visco-plasticity- plasticity and creep in elastic solids-a unified numerical solution approach [J]. International Journal for Numerical Methods in Engineering,1974,8(4): 821-845.

[12] 闫守海. 钢材高温蠕变性能试验研究[D]. 重庆：重庆大学，2015. Yan S H. Experimental study on creep behavior in steel at elevated temperatures [D]. Chongqing: Chongqing University,2015. (in Chinese)

[13] Poh K W. Stress-strain-temperature relationship for structural steel [J]. Journal of Materials in Civil Engineering,2001,13: 371-379.

[14] Liu T C H,Fahad M K,Davies J M. Experimental investigation of behavior of axially restrained steel beams in fire [J]. Journal of Constructional Steel Research,2002,58(9): 1211-1230.

[15] Luecke W E,McColskey J D,McCowan C N,et al. Federalbuilding and fire safety investigation of the World Trade Center Disaster: mechanical properties of structural steels. NIST NCSTAR 1-3D [R]. Gaithersburg,MD: National Institute of Standards and Technology,2005.

(编辑 胡英奎)

Effect of creep models on the fire resistance analysis of restrained steel beams

WangWeiyonga,b,HePingzhaoa

(a.School of Civil Engineering; b.Key Laboratory of New Technology for Construction of Cities in Mountain Area (Ministry of Education),Chongqing University,Chongqing 400045,P. R. China)

Significant creep deformation occurs in steel subjected to elevated temperatures and loading,and thus affects the deformation and load capacity of steel Structures in fire. Currently there are many creep models,which are not widely suitable. Significant effect on fire resistance analysis of steel beam can be observed using different creep models. In order to quantity this effect,comparison was made to analyze five kinds of creep model. Fire resistance of restrained beam under five creep models was analyzed using computer program and the results were compared with test data. Norton creep model revealed best agreement with test data. Finally,parametric study was conducted on the parameters affecting the fire resistance of restrained steel beams. It is showed that Harmathy creep model had a greatest effect on fire response of restrained steel beams. The degree of creep influence to fire resistance of restrained steel beams for different creep models under different load ratio and restraint were different.

creep model; restrained beam; fire resistance;steel structure

10.11835/j.issn.1674-4764.2015.05.006

2015-07-20 基金项目：中央高校基本科研业务费(CDJZR12200004)；重庆市自然科学基金(cstc2013jcyjA30010)

王卫永(1982-)，男，博士，副教授，主要从事结构抗火性能研究，(E-mail)wywang@cqu.edu.cn。

Foundation item：Fundamental Research Funds for the Central Universities,China (No. CDJZR12200004);Natural Science Foundation of Chongqing(No. cstc2013jcyjA30010)

TU392

A

1674-4764(2015)05-0041-07

Received:2015-07-20

Author brief：Wang Weiyong (1982-),PhD,associate professor,mail research interest: fire resistance of structures,(Email) wywang@cqu.edu.cn.