复杂疾病的系统医学视角：内源性网络理论*

苏 杭，王高伟，朱晓梅，徐岷涓，敖 平③†

①上海交通大学系统生物医学研究中心教育部重点实验室，上海 200240；②基因计算公司，西雅图 WA 98105，美国；③上海交通大学癌基因及相关基因国家重点实验室，上海 200240

复杂疾病的系统医学视角：内源性网络理论*

苏 杭①，王高伟①，朱晓梅②，徐岷涓①，敖 平①③†

①上海交通大学系统生物医学研究中心教育部重点实验室，上海 200240；②基因计算公司，西雅图 WA 98105，美国；③上海交通大学癌基因及相关基因国家重点实验室，上海 200240

随着分子生物学的发展，对表型背后复杂的分子调控机制进行系统和定量分析成为当前重要研究方向之一。内源性网络理论提供了一种可行的方法，可以通过总结已有的生物学知识构建系统核心调控网络，并利用非线性随机动力系统对网络进行定量分析。本文主要回顾了内源性网络理论的核心内容及迄今为止基于该理论框架下所取得的成果。在内源性网络理论框架下，我们可以利用功能性景观理解复杂疾病的发生发展过程，作出可验证的全新预测，进而为复杂疾病预防、诊断、治疗提供一系列潜在的思路和方案。

内源性网络理论；非线性随机动力学系统；复杂疾病；系统生物学；稳态；亚稳态；临界态

随着社会发展和生活水平的提高，慢性非传染性疾病，包括肿瘤、心脑血管疾病、代谢性疾病(如肥胖和糖尿病)和神经退行性疾病(如阿尔兹海默症)等，逐渐发展成为严重危害人类健康的主要疾病[1-2]。探究这些复杂疾病发生发展背后的分子机制，进而对其进行有效的预防和控制，是生物医药界长久以来不懈追求的目标。

自DNA双螺旋结构发现后，在很短的时间内，遗传学和分子生物学的发展实现了巨大的飞跃。人们将表型还原到分子层次，研究特定分子的行为对表型的影响，并取得了包括中心法则在内的大量重要的研究成果[3-4]。人类基因组计划的实施和完成，更成为分子生物学发展过程中里程碑式的进步[5-7]。人们希望通过这项宏伟的计划，可以破译生命密码，解开全部生命的疑团。然而基因组计划完成十多年，许多疾病，尤其是癌症一类复杂性疾病，其发病和死亡的人数呈逐年上升趋势，并没有因基因序列的破译而在诊疗方面取得突破。传统的“一基因，一疾病”的观点——即个别基因或者蛋白质的异常变化是疾病发生发展的主要原因，在应对如癌症等复杂疾病的过程中遇到瓶颈[8-9]。

越来越多的实验数据和理论分析显示，癌症等复杂性疾病的发生和发展通常是由于遗传因素与环境因素长期相互作用的结果[10-13]。事实上，生物系统中功能的实现只有极少数情况下是由单个分子承担的。很多生物现象，从细胞周期到人类复杂疾病的发生发展过程，其背后涉及到的分子调控机制非常复杂。基因和蛋白质等分子之间通过广泛的非线性相互作用关系形成了复杂网络[14-16]，大量反馈的存在使得系统动态变化过程中并没有简单的因果关系区分，很难对其动力学行为直观地进行预测。在针对类似复杂系统的研究过程中，传统的单基因或单蛋白的“碎片化”研究方法显然已经不再足够。以整体和定量研究为特征的系统生物学方法应运而生，将还原论和整体论辩证统一地结合在一起[17-20]。有趣的是，这种强调整体和系统的研究思路，与古老的中国传统医学所强调的“整体观”和“辩证施治”极为相似[21]。

事实上，早在20世纪，表型是由分子之间形成的复杂网络实现及类似的观点已经被提出[18,22-24]。然而，由于当时分子水平研究基础薄弱及数学方法的制约，科学家们虽然预见到了未来生物界趋向于系统的发展趋势，但并没有给出具体的方法来建立和分析这样的网络。而今，随着分子生物学的飞速发展，大量分子水平研究成果呈指数爆炸式积累；与此同时，随机过程等数学工具的发展，为描述网络的动力学过程提供了新的可能[25-26]。生物界迫切地需要一个统一的理论框架来归纳已有的生物知识，解释和预测实验现象，还原生物系统的全貌——从系统生物学角度来对生命现象背后复杂的分子调控机制进行研究的时机已经成熟。

基于以上种种背景和需要，内源性网络理论提出了一类可行的方法对生物系统中复杂的分子调控网络进行概括性描述和定量分析[14,16,27]。内源性网络指在长期演化过程中形成的核心调控网络，由信号转导和基因调控两部分组成，具有保守性、模块化、闭合自治性等基本特点。这一定量框架可以进一步应用于包括癌症在内的许多复杂疾病的研究中，从随机动力学的角度重新解读其发生发展过程，并做出一系列可验证的全新预测，进而为复杂疾病的预防、诊断和治疗提供一些可行的思路和方案。

在下文中，我们将一一介绍内源性网络理论中的一些基本假设，以及迄今为止基于该理论框架的相关研究所取得的主要进展。

1 内源性网络理论

生物系统调控网络经由长期演化过程形成，内源性网络理论假设所有生物体的调控网络遵循统一的设计原则。通过总结生物系统中的一般规律，理论提出了生物系统核心网络设计结构可能的一些特征，其中一些基本假设已在模式生物λ噬菌体中得到例证[28]。在该理论框架下，我们可以通过总结分子生物学知识和已有的实验数据，构建生物系统核心网络。

接下来，我们将讨论内源性网络的几个基本特性。

1.1 保守性和稳定性

生物系统的核心调控网络是在长期的演化过程中逐步形成的，一些执行关键功能的模块和通路具有非常保守的特性。事实上，包括细胞周期、凋亡在内的许多重要功能模块相关研究的突破，最初都是在简单模式生物如酵母、线虫等的研究中所取得的[29-30]。核心内源性网络中的节点和相互作用关系十分保守和稳定，这使得通过总结生物学现有知识和实验数据构建核心网络成为可能。更重要的意义在于，在一个生物个体有限的一生中，不太可能发生内源性网络最核心结构的改变，因而大部分复杂疾病是有机会发生逆转的[16]。

1.2 模块化和层次性

功能模块是指其功能与其他模块相互区别的独立实体[31]，这一概念被广泛应用于生物系统当中，如细胞周期、凋亡、信号转导通路等等。关于模块的存在与否，可以通过将某种特异的功能模块移植入不同类型的细胞来进行验证，如将离子通道和泵植入非兴奋性细胞[32]。

大多数功能模块是由多个分子通过复杂的相互作用形成的具有特定功能的实体结构，很难通过研究单一组分而获得模块功能的全部信息。然而，功能模块中依然存在有限个关键调控因子(如Phage lambda双稳态基因开关中的Cro和CⅠ蛋白[28,33])，它们的表达和活化与否会决定功能模块最终的状态。

基于此，我们假设每个模块可以由一组关键的分子来近似刻画，这些分子通过信号转导和基因调控相互影响，形成一些闭合的子网络。由于蛋白质是生物功能的最终执行者，我们在建网过程中主要选择蛋白质作为节点，并在此基础上进行合理的简化，从而构建出反映功能模块执行状态的核心网络结构。参考和总结前期的工作[34-36]，我们重新绘制出与人体组织特异性相关的内源性网络核心模块(图1)。

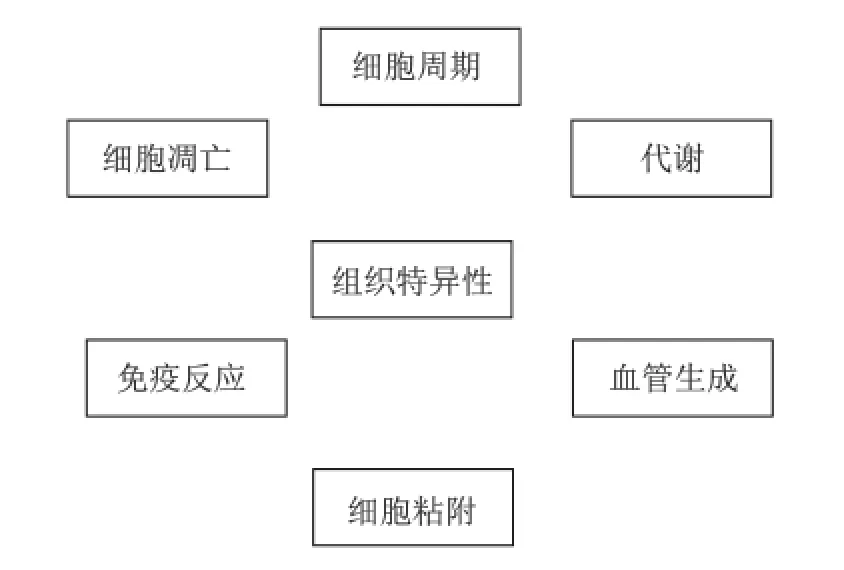
图1 人体组织特异性内源性网络核心模块[34-36]。人体组织特异性内源性网络核心模块包含细胞周期、凋亡、代谢、免疫反应、细胞粘附、血管生成等。这些模块由相关的分子通过复杂的非线性相互作用形成，独立执行某些特殊功能。模块与模块之间相互联系，形成内源性网络。该图通过总结内源性网络前期工作中模块的筛选和构建情况绘成

1.3 封闭性、自治性和内稳态

由于生物系统中存在大量的反馈调控，系统中信息的传递并不是像中心法则那样的单向过程。相反，在网络的动力学过程中很难找到简单的因果区分[24]。在内源性网络理论框架下，关键的分子之间通过信号转导和基因调控互相作用，形成一个层次分明的闭合自治网络。将这样的闭合自治网络转化为一套非线性随机动力系统进行定量分析，通常会找到一些非常稳定的局部稳态。这些稳态带有明显或不明显的生物学功能：一部分稳态可能具有正常功能，如细胞正常的生长和凋亡等；另外一些功能则可能是少见的，但对生物体仍具有一定意义，如应激状态等。这种闭合网络能够很好地解释生物学中的反馈调控的重要意义，同时也体现了生物系统中所特有的适应性和稳定性等性质。

综上所述，在内源性网络理论框架中，保守的关键分子(基因、蛋白等)通过相互作用关系形成了一些执行特定功能的独立模块，这些模块之间互相影响，共同构成生物系统复杂调控网络。内源性网络具有稳定性、封闭性和自治性等特征，并可以产生多个内稳态。图2以肝细胞肝癌内源性网络模型[34]为例，展示了内源性网络的重要节点和基本拓扑结构。

2 从内源性网络到非线性随机动力学系统

定量数学模型可以对生物系统进行精确的描述和分析，尤其对于复杂系统而言，数学定量模型的构建和分析可以帮助我们思考和推理，从而得到许多仅靠直觉和简单逻辑推理无法获得的结论和预测[37-38]。

接下来，我们在标准的定量框架下[39-41]，用一组随机微分方程(SDE)来描述网络中节点与节点之间的相互作用关系。系统中任意一个节点的浓度或活性随时间变化的趋势，均可用随机微分方程进行描述。以蛋白χ1为例，其浓度(活性)相关的随机微分方程如下所示：

其中，χ1(t)代表t时刻蛋白χ1的浓度或活性，表示在t时刻蛋白χ发生降解或失活的速率，1ξ(X,t)代表系统噪声，f1(X)代表蛋白χ1的合成速率。f1(X)值受到其他因子对蛋白χ1的作用影响，可用以下式子进行表示：

其中，Vmax代表蛋白χ1最大合成速率, Xa代表所有对蛋白χ1具有激活作用的因子浓度或活性，Xi代表所有对蛋白χ1具有抑制作用的因子浓度或活性，ka、ki分别为反映激活和抑制关系的常数，na、ni为相关激活或抑制反应中的希尔系数。由于复杂系统的动力学过程中涉及大量的参数，多数找不到相应的实验测量数据进行支持，参数取值问题也涉及许多争议[42-43]，如何选取一种合理的办法来解决参数问题，成为动力学建模的一个难点。

种种研究表明，生物系统具有非常强的稳定性，对相关参数的改变并不敏感，网络的拓扑结构本身决定了生物系统的稳定性和适应性[18,44]。因而在一个结构合理的内源性网络中，参数在合理范围内的变化不会影响最终的结果。基于此，我们对以上公式进行归一化处理，使Vmax=1；由于在生化反应过程中，体内绝大部分协同希尔系数为2～5[45]，统一选取3作为所有激活抑制反应的希尔系数，速率常数k值取在8左右。通过以上方法，我们将所构建的核心内源性网络转化为一套非线性随机动力系统，并进行动力学分析。通过随机选取网络节点初始值，我们对网络随时间演化的过程进行模拟，并寻找网络最终的稳定状态。

为了验证假设是否正确，我们用多种可行的方程形式对网络结构进行描述，并使参数在合理的范围内进行变化，发现网络在不同的定量描述方程形式和参数条件下，一部分稳定始终可以非常稳定地存在[34-36]。该结果进一步支持和验证了已往关于生物系统稳定性的研究，同时也反映了依照内源性网络理论所构造网络的合理性及可行性，从而为进一步研究奠定基础。

图2 肝细胞肝癌内源性网络[34]。保守的关键分子通过相互作用关系形成了一些执行特定重要功能的独立模块，这些模块通过模块间交叉的相互作用、相互影响，共同构成组织特异性相关的的内源性网络

3 内源性网络在复杂疾病中的应用

在内源性网络的理论框架下，正常组织的发育及功能执行与该组织相关疾病的发生和发展受同一个核心内源性网络调控。由于网络节点之间非线性动力学的相互制约，在不同的初始条件下，网络随时间的演化会稳定在不同的局域稳态[46-47]。在不同的状态下，核心网络中相关的节点表达形成独特的子网络发挥作用，并最终产生特异的表型和功能，因而可以将正常和癌症状态看作该内源性网络中的不同稳态。

在接下来的工作中，我们惊喜地发现，网络产生的稳定状态中，对参数和方程形式不敏感的稳态通常对应着明确的生物学意义。模型计算结果中部分稳态的节点表达情况与不同表型(癌症与正常组织)所对应的生物学实验及芯片数据均有良好的对应[34-36]。至此，我们从生物学知识出发，构建与疾病相关的核心内源性网络，以稳态的概念成功地将一些生物学现象与分子调控机制联系在一起，并与已有的低通量实验和高通量数据等不同的数据类型皆有良好的对应。需要强调的是，我们构建网络时所依据的是从不同文献和综述中独立获取的与生物学机制相关的知识，并不涉及基因表达数据的统计和分析。由于高维非线性复杂网络其动力学行为非常复杂难以预测，从已知的机制出发进行建模和动力学模拟，可以重复出与表型相关的基因表达，并且与多种类型的实验数据有良好的吻合，这样的结果是十分令人惊喜和振奋的。

更有意义的是，在内源性网络的基础上，我们还可以做出一些宏观的预测，从而对癌症等复杂疾病的预防和治疗提出一些潜在的思路和方法。

图3 人类癌症功能性景观中的三种典型状态：稳态、亚稳态、临界态[14]。这是功能性景观中的三种典型状态，其中，纵向空间代表稳态的相对稳定性，横向空间代表不同稳态的吸引域。(a)在正常状态下代表健康的稳态是全局稳态；(b)由于基因、表观遗传学及环境因素的变化对内源性网络功能性景观产生影响，疾病稳态变为比健康稳态更加稳定，使得健康状态成为一种亚稳态。在这种情况下，对于整个机体而言健康状态依然能维持相对较长时间的稳定；(c)内源性网络受到基因、表观遗传学及环境因素的重大影响而产生的一种极端的状态，在这种情况下，健康稳态受到完全的破坏，乃至不能维持局域稳定性

首先，在内源性网络理论框架下，网络中产生的局部稳态带有明显或不明显的生物学功能。一些稳态可能具有正常功能，如细胞正常的生长和凋亡；另外一些功能则可能是少见的，但对生物体仍具有一定意义，如应激状态等。如果在给定条件下，网络所处稳态并非对生物体的最优选择，则生物体就会“生病”，因而可以把该类稳态称为“疾病状态”[14]。癌症等复杂疾病的产生和发展则被认为是在同一个核心网络中，从代表正常状态的稳态逐步转换到代表疾病状态的稳态的过程。网络可以自发地决定其所处的稳态，并停留在任何一种稳态中很长时间。与此同时，网络从一个稳态转换为另一个稳态的过渡存在偏好的路线，表明以癌症为代表的复杂性疾病的发生和发展具有一定的模式；如果将一个稳态转换到另外一个稳态看作一步过程，网络中多稳态的存在也可以很好地解释癌症的发生发展需要多步及长时间的积累这一现象[14]。如图3所示，利用功能性景观，我们可以直观地理解稳态之间的相互转换及其所偏好的路径，从动力系统稳态、亚稳态到临界态的角度来理解健康、亚健康到疾病状态的发展过程[48]。

第二，影响稳态发生转变的因素有很多，如基因突变等导致的网络结构变化，随机性引起的基因调控和信号转导噪声等等。由此得出的一个重要推论是，突变并非癌症产生的唯一驱动力，因而在内源性网络框架下，临床上观测到的没有明显突变的癌症病例可以顺理成章地得到解答[49-50]。

第三，由于内源性网络是在长期的演化过程中形成，具有很强的稳定性，稳定的网络系统可以被认为是生物体内产生的多种多样突变的“缓冲剂”[51]。基于此，我们预测在正常组织中同样存在大量的突变，并具有一定的规律。在最近发表的文章中，人们通过实验和数据分析发现正常组织样本中突变的确大量存在[52]，初步印证了我们的预测。同时，由于核心网络结构的稳定性，我们预测绝大部分癌症患者体内核心网络结构并没有发生根本的破坏，因而大多是可以逆转，即可以被治愈的。在一些特定的情况下，系统甚至不需要外界干预就可以完成这一过程——这也解释了在一些少数的临床案例中，癌症患者自发的好转现象[53-55]。

第四，通过网络分析，我们进一步发现，癌症和正常状态是由不同的正反馈进行维持的。因而一个合理的预测是，由于生物系统内源性网络本身的复杂性和稳定性，单靶点用药可能对癌症治疗来说是不够的。我们预测针对不同反馈环的联合用药，通过破坏维持癌症状态的正反馈和激发维持正常状态的正反馈来从根本上抑制癌症的发展，可以作为未来癌症治疗策略之一[34]。

迄今为止，与肝癌、胃癌、前列腺癌、阿尔兹海默症相关的内源性网络研究工作取得初步进展，并对癌症的发生及维持机制、治疗策略，异质性的产生原因等问题进行了一定的解答和预测[34-36,56]；模式生物酿酒酵母生长相关的内源性网络研究工作也取得了初步进展[57]。随着工作的深入，我们会对复杂疾病的发生发展产生更加深入的理解，并逐步将这套建模和定量分析方法应用于临床实践中，为其预防、诊断、治疗提供一系列潜在的观点和方案。

接下来，我们将针对内源性网络理论未来可能的临床应用做一系列具体的展望。

从预防角度，对于一些具有家族病史或生存环境特殊的人群，我们可以基于内源性网络并结合相关信息评估个体患病风险，并通过干预网络结构中重要的因子和改变随机因素如环境、饮食等等，来加强健康状态的稳定性，从而为疾病预防提供一些可行的方案。

在诊断方面，对内源性网络进行动力系统分析可以准确计算出鞍点的特征，从而提供由健康状态转变到疾病状态过程中重要的临界标准：若系统尚未跨越鞍点，则停止病因刺激能够自发恢复健康状态；若已跨越鞍点，则需要持续、有效的治疗和干预才能使病人恢复健康。在未来，通过综合病人基因组和表观遗传学多个方面特征信息，结合网络鞍点评价病人疾病发展阶段，我们可以基于内源性网络理论框架发展出一套系统的早期诊断标准，从而更好地为个体化诊疗及精确医疗相关的临床实践服务。

有关复杂疾病的治疗策略，我们已在前期工作中进行了一部分讨论[34]。通过网络分析，我们发现网络中不同的稳态由不同的正反馈维持其稳定性。由于正反馈的存在，单靶点药物治疗的效果具有很大的局限性。针对状态维持的关键调控机制，激活正常状态正反馈、抑制疾病状态正反馈多靶点联合用药，可以作为未来复杂疾病治疗策略之一。利用内源性网络进行计算机模拟和用药靶点组合式筛选，可以极大地降低药物筛选工作量，实现联合用药治疗策略，结合个体差异帮助医药工作者根据病人实际情况制定可行的个体化治疗方法。

4 总结与讨论

随着现代生命科学的发展，大量的证据表明，生命现象背后的调控机制涉及到非常复杂的非线性网络系统，传统的“一基因，一疾病”的观点已无法充分解释复杂性疾病的发生和发展过程中出现的一些现象。本文主要回顾了内源性网络理论的基本内容，包括复杂生物系统调控网络构建和定量分析相关的一系列原则、方法和手段，以及迄今为止在该理论框架下所取得的进展。内源性网络理论认为，生物系统在长久的演化过程中，形成了保守的、自治的核心内源性网络，实现并调控生物体生长、繁殖等一系列生命活动。内源性网络结构遵循演化所形成的统一的设计原则，具有高度的保守性和稳定性。在内源性网络理论框架下，组织正常功能和疾病状态受同一个核心网络调控，在不同的状态下，由网络中不同子网络执行特异性功能，疾病和正常状态可以被认为是同一个内源性网络中的不同稳态。我们通过总结现有的分子生物学知识和实验数据，构建核心内源性网络，将其转化为一套非线性随机动力系统进行定量分析，并取得相应预测。在前期工作当中，我们构建出与肝癌、胃癌、前列腺癌等疾病相关的核心内源性网络，解释了目前主流癌症发生发展理论框架下难以解答的多种临床现象，诸如癌症的自发好转、无明显突变的癌症案例等，并取得了包括癌症维持机制、异质性产生机制、癌症治疗策略等一系列预测。我们相信，在接下来的工作当中，通过理论数学建模和实践之间的相互促进，可以得到对复杂性疾病的更好理解，最终实现复杂性疾病诊疗方面的新突破。

致谢 感谢上海交通大学敖平课题组李斯特、王俊强、袁若石等同学的建议和帮助。

(2015年7月16日收稿)

[1] WORLD HEALTH ORGANIZATION. Preventing chronic diseases: a vital investment [R]. WHO global report, 2005.

[2] MOUSSAVI S, CHATTERJI S,VERDES E, et al. Depression, chronic diseases, and decrements in health: results from the World Health Surveys [J]. Lancet, 2007, 370(9590): 851-858.

[3] ALBERTS A, JOHNSON A, LEWIS J, et al. Molecular biology of the cell [M]. 4th ed. New York: Garland Science, 2002.

[4] WATSON J D, BAKER T A, BELL S P, et al. Molecular biology of the gene [M]. 6th ed. San FranciscoCold Spring Harbor, N.Y.: Pearson/ Benjamin Cummings; Cold Spring Harbor Laboratory Press, 2008.

[5] ADAMS M D, KELLEY J M, GOCAYNE J D, et al. Complementary DNA sequencing: expressed sequence tags and human genome project [J]. Science, 1991, 252(5013): 1651-1656.

[6] VENTER J C, ADAMS M D, MYERS E W, et al. The sequence of the human genome [J]. Science, 2001, 291(5507): 1304-1351.

[7] LANDER E S, LINTON L M, BIRRE N B, et al. Initial sequencing and analysis of the human genome [J]. Nature, 2001, 409(6822): 860-921.

[8] HUANG S, ERNBERG I, KAUFFMAN S. Cancer attractors: a systems view of tumors from a gene network dynamics and developmental perspective [J]. Semin Cell Dev Biol, 2009, 20(7): 869-876.

[9] 吴克复. 免疫的细胞社会生态学原理[M].北京: 科学出版社, 2012.

[10] WYNDER E L, GRAHAM E A. Tobacco smoking as a possible etiologic factor in bronchiogenic carcinoma: a study of 684 proved cases [J]. J Am Med Assoc, 1950, 143(4): 329-336.

[11] NOWELL P C. The clonal evolution of tumor cell populations [J]. Science, 1976, 194(4260): 23-28.

[12] LEY R E, TURNBAUGH P J, KLEIN S, et al. Microbial ecology: human gut microbes associated with obesity [J]. Nature, 2006, 444(7122): 1022-1023.

[13] ESTELLER M. Epigenetics in cancer [J]. N Engl J Med, 2008, 358(11): 1148-1159.

[14] AO P, GALAS D, HOOD L, et al. Cancer as robust intrinsic state of endogenous molecular-cellular network shaped by evolution [J]. Med Hypotheses, 2008, 70(3): 678-684.

[15] AUFFRAY C, IDEKER T, DAVID J, et al. The hallmarks of cancer revisited through systems biology and network modelling [M]// CESARIO A, MARCUS F. Cancer Systems Biology, Bioinformatics and Medicine. New York: Springer, 2011: 245-266.

[16] WANG G W, ZHU X M, HOOD L, et al. From Phage lambda to human cancer: endogenous molecular-cellular network hypothesis [J]. Quantitative Biology, 2013, 1(1): 32-49.

[17] HOOD L. Systems biology: integrating technology, biology, and computation [J]. Mechanisms of Ageing and Development, 2003, 124(1): 9-16.

[18] KITANO H. Systems biology: a brief overview [J]. Science, 2002, 295(5560): 1662-1664.

[19] NURSEP, HAYLES J. The cell in an era of systems biology [J]. Cell, 2011, 144(6): 850-854.

[20] 贾伟, 敖平, 王晓艳. 代谢组学: 系统生物医学的关键角色 [J]. 科学, 2012, 64(6): 12-15.

[21] 沈自尹. 系统生物学和中医证的研究 [J]. 中国中西医结合杂志, 2005, 25(3): 255-258.

[22] WRIGHT S. The roles of mutation, inbreeding, crossbreeding, and selection in evolution [C]//JONES D F.Proceedings of the sixth International Congress of Genetics, Ithaca, New York, 1932. New York: Brooklyn Botanic Garden, 1932.

[23] WADDINGTON C H. The strategy of the genes [M]. London: Routledge, 2014.

[24] NOBLE D. Claude Bernard, the first systems biologist, and the future of physiology [J]. Exp Physiol, 2008, 93(1): 16-26.

[25] AO P. Potential in stochastic differential equations: novel construction [J]. Journal of Physics A: Mathematical and General, 2004, 37(3): L25.

[26] YUAN R S, AO P. Beyond itô versus stratonovich [J]. Journal of Statistical Mechanics: Theory and Experiment, 2012(07): P07010.

[27] 敖平,等. 肿瘤发生发展的内源性网络假说[M]//中国科学技术协会. 2012—2013 生物化学与分子生物学学科发展报告. 北京:中国科学技术出版社, 2014: 181-182.

[28] ZHU X M, YIN L, HOOD L, et al., Efficiency, robustness, and stochasticity of gene regulatory networks in systems biology: λ switch as a working example [M]// CHOI S. Introduction to Systems Biology. New York: Springer, 2007: 336-371.

[29] HARTWELL L H, MORTIMER R K, CULOTTI J, et al. Genetic control of the cell division cycle in yeast [J]. Science, 1974, 183(4120): 46-51.

[30] BRENNER S. The genetics of Caenorhabditis elegans [J]. Genetics, 1974,77(1): 71-94.

[31] HARTWELL L H, HOPFIELD J J, LEIBLER S, et al. From molecularto modular cell biology [J]. Nature, 1999, 402: C47-52.

[32] HSU H, HUANG E, YANG X C, et al. Slow and incomplete inactivations of voltage-gated channels dominate encoding in synthetic neurons [J]. Biophys J, 1993, 65(3): 1196-1206.

[33] PTASHNE M. A genetic switch: phage lambda and higher organisms [M]. 2nd ed. Cambridge: Blackwell Scientific Publications, 1992 .

[34] WANG G W, ZHU X M, GU J, et al. Quantitative implementation of the endogenous molecular-cellular network hypothesis in hepatocellular carcinoma [J]. Interface Focus, 2014, 4(3): 20130064.

[35] LI S T, ZHU X M, LIU B Y, et al. Endogenous molecular network reveals two mechanisms of heterogeneity within gastric cancer [J]. Oncotarget, 2015, 6(15): 13607-13627.

[36] ZHU X M，YUAN R S，HOOD L, et al. Endogenous molecularcellular hierarchical modeling of prostate carcinogenesis uncovers robust structure [J]. Prog Biophys Mol Biol, 2015, 117(1): 30-42.

[37] MOGILNER A, WOLLMAN R, MARSHALL W F. Quantitative modeling in cell biology: what is it good for? [J]. Dev Cell, 2006, 11(3): 279-287.

[38] LE NOVERE N. Quantitative and logic modelling of molecular and gene networks [J]. Nat Rev Genet, 2015, 16(3): 146-158.

[39] GLASS L, KAUFFMAN S A. The logical analysis of continuous, nonlinear biochemical control networks [J]. J Theor Biol, 1973, 39(1): 103-129.

[40] TYSON J J, CHEN K C, NOVAK B. Sniffers, buzzers, toggles and blinkers: dynamics of regulatory and signaling pathways in the cell [J]. Curr Opin Cell Biol, 2003, 15(2): 221-231.

[41] AO P，GALAS D，HOOD L, et al. Towards predictive stochastic dynamical modeling of cancer genesis and progression [J]. Interdiscip Sci, 2010, 2(2): 140-144.

[42] DYSON F. A meeting with Enrico Fermi [J]. Nature, 2004, 427(6972): 297.

[43] MAYER J, KHAIRY K, HOWARD J. Drawing an elephant with four complex parameters [J]. American Journal of Physics, 2010,78(6): 648-649.

[44] BARKAI N, LEIBLER S. Robustness in simple biochemical networks [J]. Nature, 1997, 387(6636): 913-917.

[45] AHRENDS R, OTA A, KOVARY K M, et al. Controlling low rates of cell differentiation through noise and ultrahigh feedback [J]. Science, 2014, 344(6190): 1384-1389.

[46] BAR-YAM Y, HARMON D, DE BIVORT B. Systems biology. Attractors and democratic dynamics [J]. Science, 2009, 323(5917): 1016-1017.

[47] DAVILA-VELDERRAIN J, MARTINEZ-GARCIA J C, ALVAREZBUYLLA E R. Epigenetic landscape models: the post-genomic era [J]. bioRxiv, 2014: 004192.

[48] AO P. Global view of bionetwork dynamics: adaptive landscape [J]. J Genet Genomics, 2009, 36(2): 63-73.

[49] VERSTEEGR. Cancer: Tumours outside the mutation box [J]. Nature, 2014, 506(7489): 438-439.

[50] OHNISHI K, SEMI K, YAMAMOTO T, et al. Premature termination of reprogramming in vivo leads to cancer development through altered epigenetic regulation [J]. Cell, 2014, 156(4): 663-677.

[51] NOBLE D. Conrad Waddington and the origin of epigenetics [J]. J Exp Biol, 2015, 218: 816-818.

[52] MARTINCORENA I, ROSHAN A, GERSTUNG M, et al. Tumor evolution. High burden and pervasive positive selection of somatic mutations in normal human skin [J]. Science, 2015, 348(6237): 880-886.

[53] CONNELLY TJ, CRIBIER B，BROWN T J, et al. Complete spontaneous regression of Merkel cell carcinoma: a review of the 10 reported cases [J]. Dermatol Surg, 2000, 26(9): 853-856.

[54] ZITO G, SAOTOME I, LIU Z Z, et al. Spontaneous tumour regression in keratoacanthomas is driven by Wnt/retinoic acid signalling crosstalk [J]. Nat Commun, 2014, 5: 3543.

[55] KIHARA K, FUJITA S, OHSHIRO T, et al. Spontaneous regression of colon cancer [J]. Jpn J Clin Oncol, 2015, 45(1): 111-114.

[56] SCHLUESENER J K, ZHU X, SCHLUESENER H J, et al. Key network approach reveals new insight into Alzheimer's disease [J]. IET Syst Biol, 2014, 8(4): 169-175.

[57] HU J, ZHU X M, WANG X W, et al. Two programmed replicative lifespans of Saccharomyces cerevisiae formed by the endogenous molecular-cellular network [J]. J Theor Biol, 2014, 362: 69-74.

Endogenous molecular-cellular network theory: A system-biomedical perspective towards complex diseases

SU Hang①, WANG Gaowei①, ZHU Xiaomei②, XU Minjuan①, AO Ping①③
①Ministry of Education Key Laboratory of Systems Biomedicine, Shanghai Center for Systems Biomedicine, Shanghai Jiao Tong University, Shanghai 200240, China; ②GenMath, Corp. 5525 27th Avenue.N.E., Seattle, WA 98105, USA; ③State Key Laboratory for Oncogenes and Related Genes, Shanghai Jiao Tong University, Shanghai 200240, China

With the development of molecular biology, it becomes increasingly important to understand the biological complexity systematically and quantitatively. Endogenous molecular-cellular network theory was proposed to depict the core network structure underneath biological system and quantify it by a nonlinear stochastic dynamical system. We review the basic considerations of this theory and several results achieved so far here. Based on this theoretical framework, we may achieve a better understanding of the progression and regression of complex diseases from an adaptive landscape view, make new and practical predictions, and provide some potentialstrategies towards the prevention, diagnosis, and treatment of these diseases.

endogenous molecular-cellular network theory, nonlinear stochastic dynamical system, complex disease, systems biology, stable state, metastable state, critical state

(编辑：段艳芳)

10.3969/j.issn.0253-9608.2015.06.008

*国家重点基础研究发展计划(973计划)(2010CB529200)和国家自然科学基金项目(NFSC91029738)资助

†通信作者，E-mail：aoping@sjtu.edu.cn