永磁同步风电系统建模及直接反馈线性化控制*
王 武
(许昌学院电气信息工程学院,河南许昌 461000)
0 引言
风能已成为解决能源危机的一种有效资源,风力发电技术得到了迅速发展,风力发电机以年总装机容量超过20%的速度递增,深入研究风力发电系统控制和设计对于促进低碳环保经济、能源可持续发展以及实现风电机组国产化具有重要理论指导意义和工程实用价值[1]。风力发电系统各个部分之间具有很强的耦合性,由于风速随机变换,使得空气动力学具有不确定性,各种电力电子变换装置具有模型复杂和非线性特征,使得风力发电系统模型为一个复杂、多变量、非线性的不确定系统[2]。传统的方法难以实现高精度控制,所以本文提出永磁同步风力发电系统的建模及直接反馈线性化控制。
永磁同步发电机具有结构紧凑、功率密度高、转矩惯性比高等一系列优点,在风电系统中得到了广泛应用。文献分析了风力机模拟中转速、转矩和功率之间的关系,实现了永磁同步电机的风力机特性模拟,并给出了转子磁场定向矢量控制算法,满足了风力机模拟的动态和稳态性能[3-4]。文献[5]对大功率直驱风力发电系统并网变流器进行了研究,论文将结合空气动力子系统、电磁子系统等实现风电系统的统一建模。然而,永磁同步电动机是一个复杂的非线性系统,其数学模型中含有角速度Ω和电流id、iq的乘积项,要实现较为精确的控制,必须对其角速度和电流进行解耦控制,同时考虑其负载扰动等因素的影响,进行必要的控制策略研究,使其达到鲁棒控制也成为风电系统研究的重点[6]。
反馈线性化控制是在一定条件下,将一个仿射非线性系统通过非线性状态反馈和恰当的坐标变换进行精确线性化,被广泛应用于各种控制系统并取得了好的控制效果[7]。文献[8]采用直接反馈线性化控制方法,实现了基于转矩扰动估计的电机反馈线性化控制,提高了跟踪快速性。文献[9]将自适应反馈线性化控制方案应用到永磁同步电机伺服系统,实现了参数在线估计,通过进行坐标变换和非线性状态反馈,达到了线性化控制。文献[10]采用状态反馈线性化理论对风轮机模型进行精确反馈线性化处理,得出其全局线性化模型并实现了桨距角最优控制。论文将结合所建模型,将直接反馈线性化控制应用于永磁同步风力发电系统,通过构建MATLAB仿真模型,通过系统仿真研究在反馈线性化控制下风电系统的性能。
1 永磁同步风电系统建模
1.1 空气动力子系统建模
根据风电系统运行中对空气动力学的描述,风力机的叶尖速度比表示叶片速度与风速之比[11]:

R为风机叶片长度;Ω1为风轮角速度;υ表示风速。
功率系数Cp用以表示风力机的风能利用效率,风力机的捕获功率可描述为:

ρ为空气密度。
转矩系数CΓ表征风轮输出转矩Γwt,可表示为:

转矩系数可以用叶尖速比λ的多项式进行描述,此处为了最优控制目的和反馈线性化计算的简化,采用叶尖速比的二阶多项式表达:

因此,风转矩可表示为风速和发电机转速为变量的表达式:
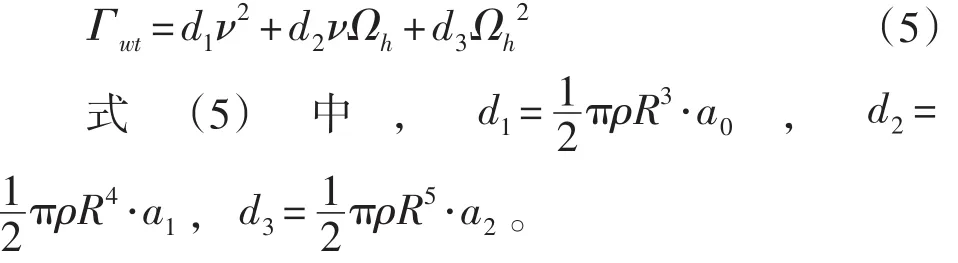
基于上述原理,在MATLAB环境下构建了空气动力子系统模型,如图1所示。
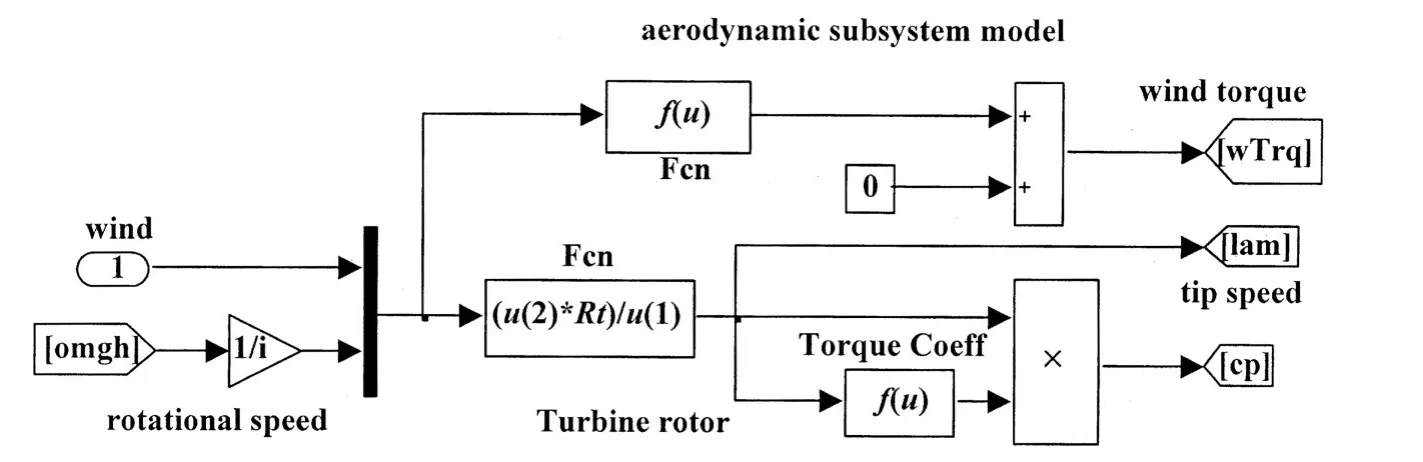
图1 空气动力子系统的MATLAB仿真模型
1.2 永磁同步风电系统建模
在永磁同步发电机模型中,忽略电机铁损、假设磁路未饱和,并假定系统定子绕组呈正弦分布,电磁对称,为了使得可以简单分析最优风能转换控制策略,此处用等效负荷代替功率元件,用常电感Ls和可变电阻Rs代替,从而对电磁子系统和电网界面进行了简化,由此构建的永磁同步风电模型用状态表达式描述为[12]:

其中:
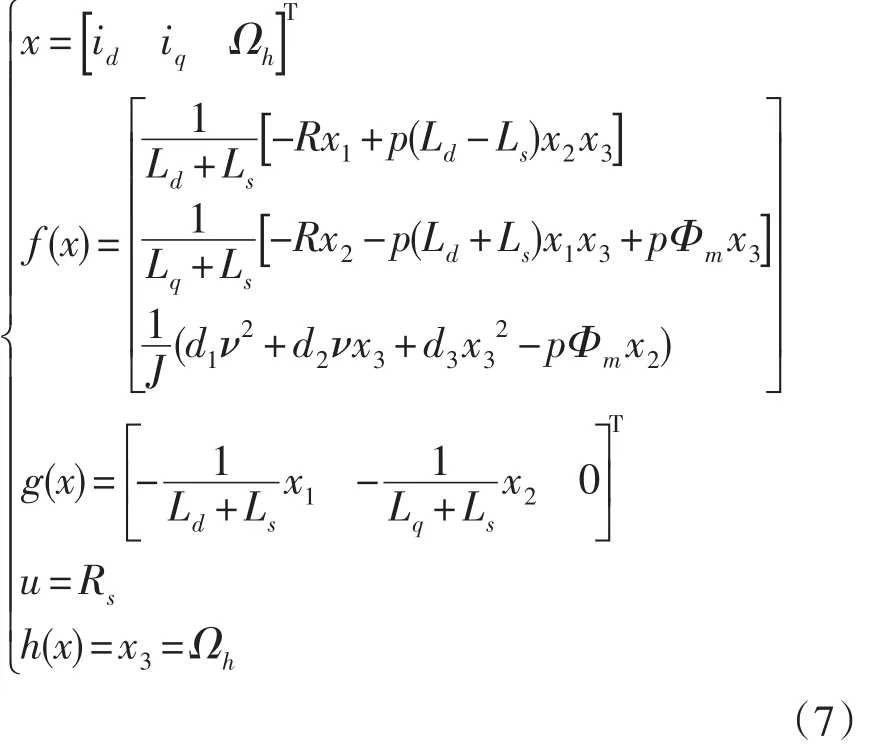
其中:p为永磁同步电机的极对数,Ωh为发电机的旋转角速度;ωs是定子的场频,R为定子电阻;Ls、Ld、Lq分别表示定子电感、d轴和q轴电感值。
在风力发电系统中,永磁同步发电机与传动机构相连,忽略系统的静态和粘性摩擦,高速轴的运动方程可表示为:
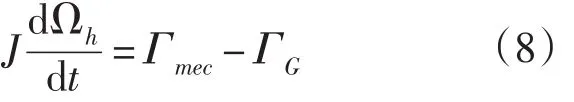
其中:J代表高速轴的转动惯量,Ωh为高速轴的旋转角速度,Γmec为机械转矩,ΓG为电磁转矩。
在MATLAB环境下构建的永磁同步风电子系统模型如图2所示。
2 永磁同步风电系统反馈线性化控制
2.1 反馈线性化控制原理
设非线性系统定义为:
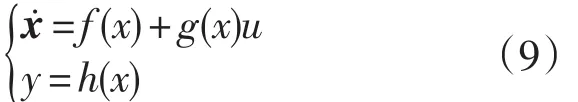
式(9)中,x是状态矢量,x∈Rn,u是输入,y是输出; f和g都是非线性平滑函数,寻找一个整数r和一个反馈[13]:

式(10)中, α(x)和 β(x)是定义在 x0∈Rn周围的平滑函数,uv是控制输入,则系统的表达式为:
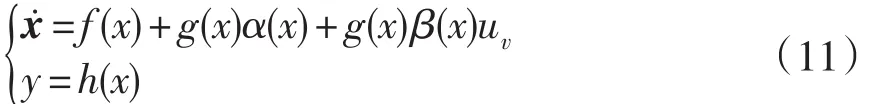
若对于每一个k<r-1和x0周围的每一个x有:
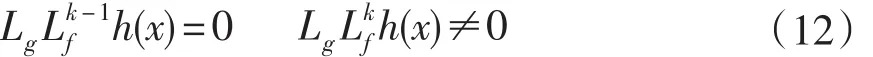
则r表示非线性系统的相关度。
为了确定系统相关度,进行如下计算:
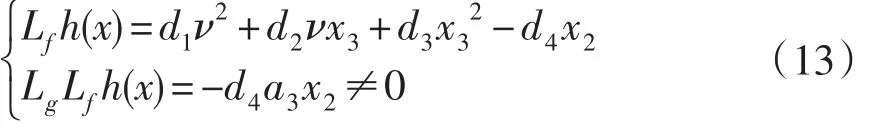
系统的相关度为2,为了将系统表达式通用化,进行坐标变换,其线性化表达式为:
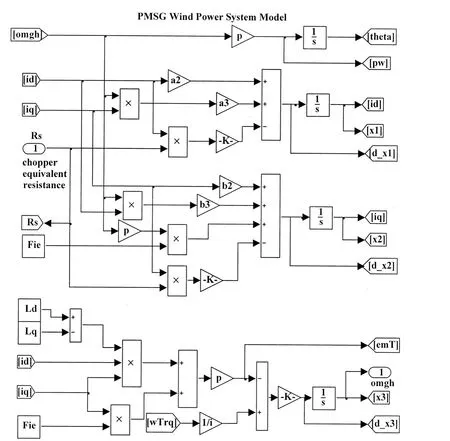
图2 永磁同步风电子系统MATLAB仿真模型
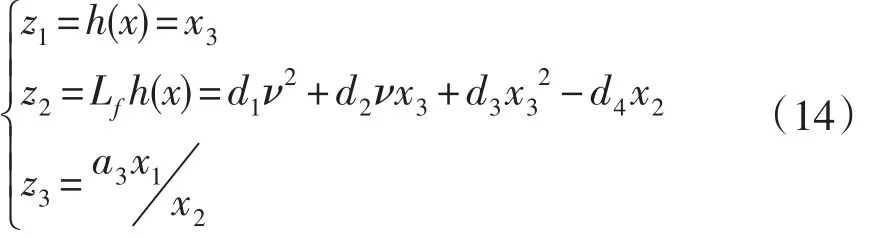
对应的逆变换为:

系统的控制输入为:
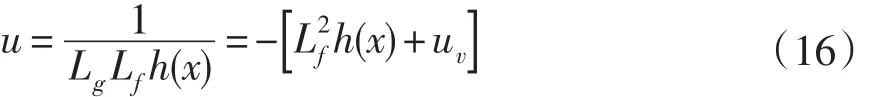
其中:
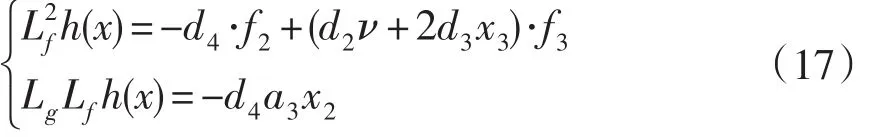
2.2 永磁同步风电系统反馈线性化控制
结合反馈线性化控制基本原理,在MATLAB环境下构建了基于反馈线性化控制的最大风能捕获控制系统,如图3所示,系统包含永磁同步风力发电系统模型、状态计算、反馈线性化控制、输入控制等部分,其核心部分为反馈线性化控制,包含坐标变换、逆坐标变换和李导数求解等模块。
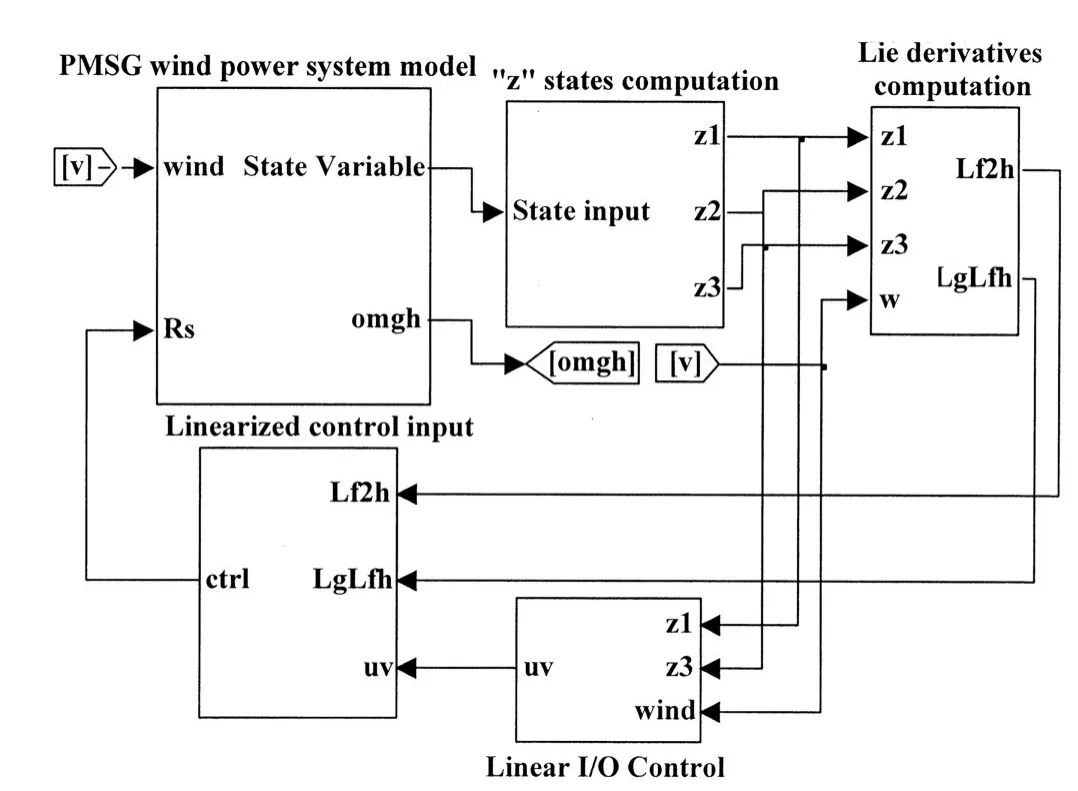
图3 永磁同步风力发电系统反馈线性化控制仿真框图
2.3 仿真及结论
在MATLAB环境下进行系统仿真,仿真时间为200秒,功率系数近似表达式中,选取参数为:
a0=0.15,a1=-0.005,a2=-0.001,系统中用到的其他相关参数见表1。

表1 系统仿真中用到的参数
给定的风速变化曲线如图4所示,反馈线性化控制曲线如图5所示,图6和图7分别给出了永磁同步发电机的d轴和q轴电流波形。对反馈线性化控制与常规PID控制下系统性能进行了比较,图8给出了叶尖速比变化曲线,图9给出了功率系数变化曲线,图10给出了最优性能跟踪曲线。通过仿真表明,论文所建永磁同步风力发电系统模型能够有效进行风电系统仿真,与传统控制方式相比较,反馈线性化控制的最优控制特性跟踪性能更好。
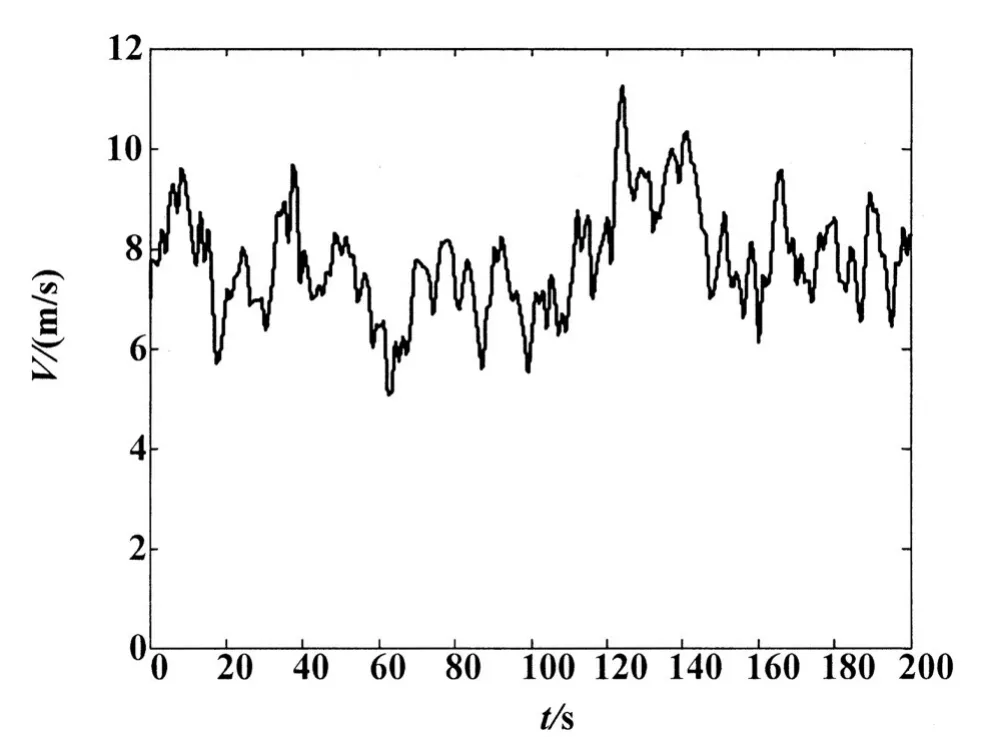
图4 风速变化曲线
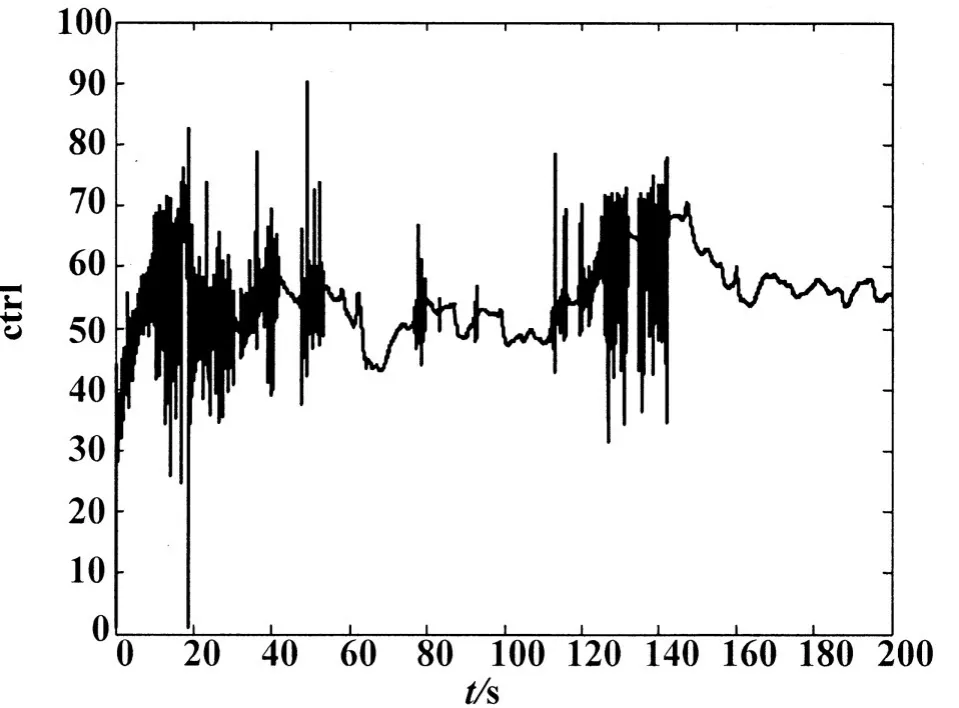
图5 反馈线新化实时控制曲线
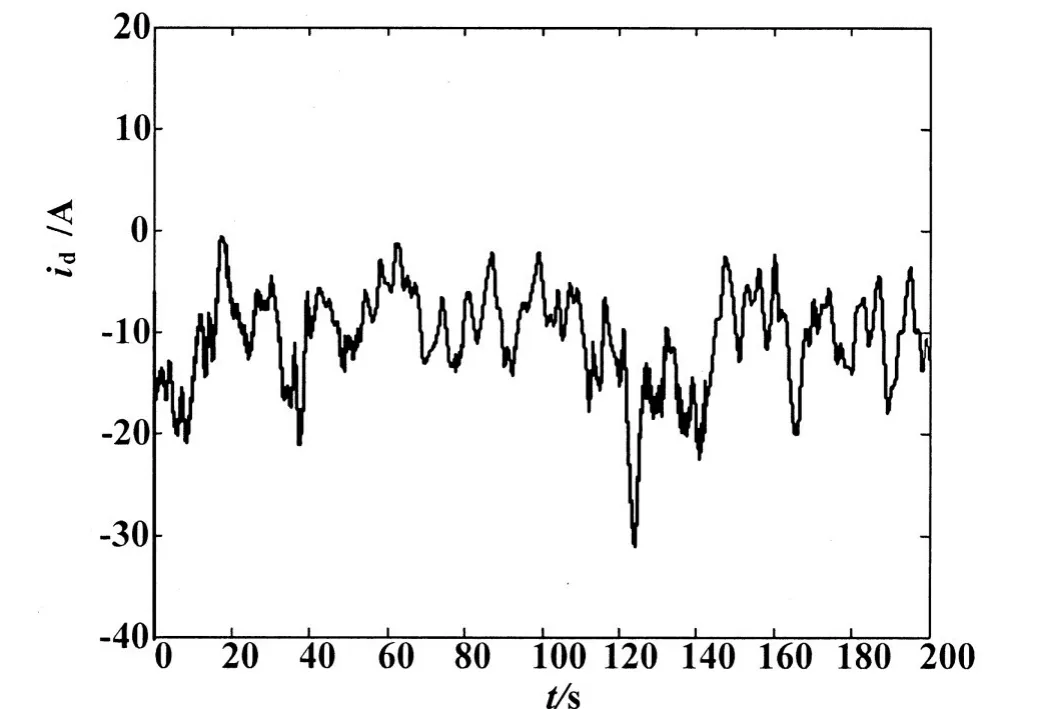
图6 d轴电流波形
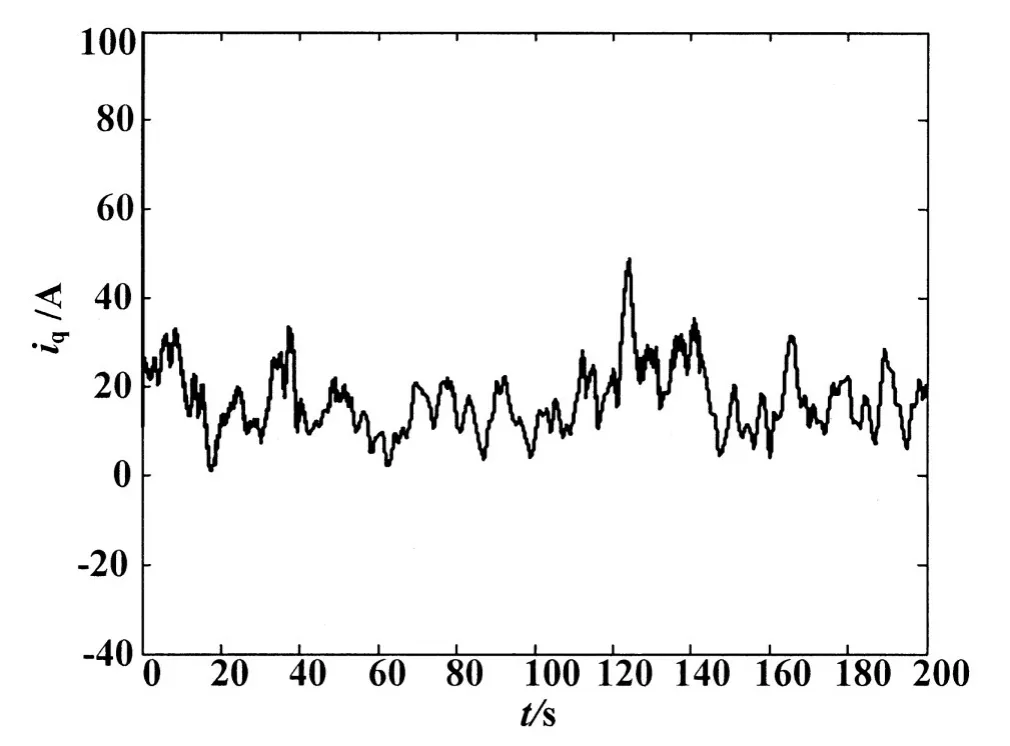
图7 q轴电流波形
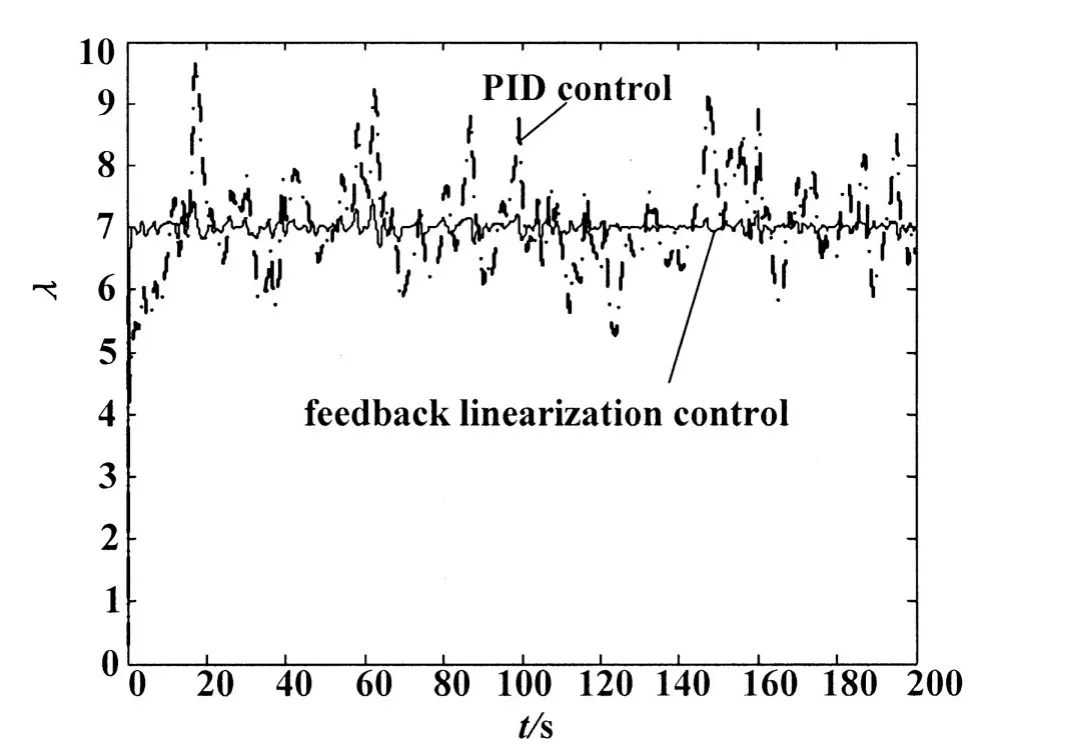
图8 叶尖速比曲线比较
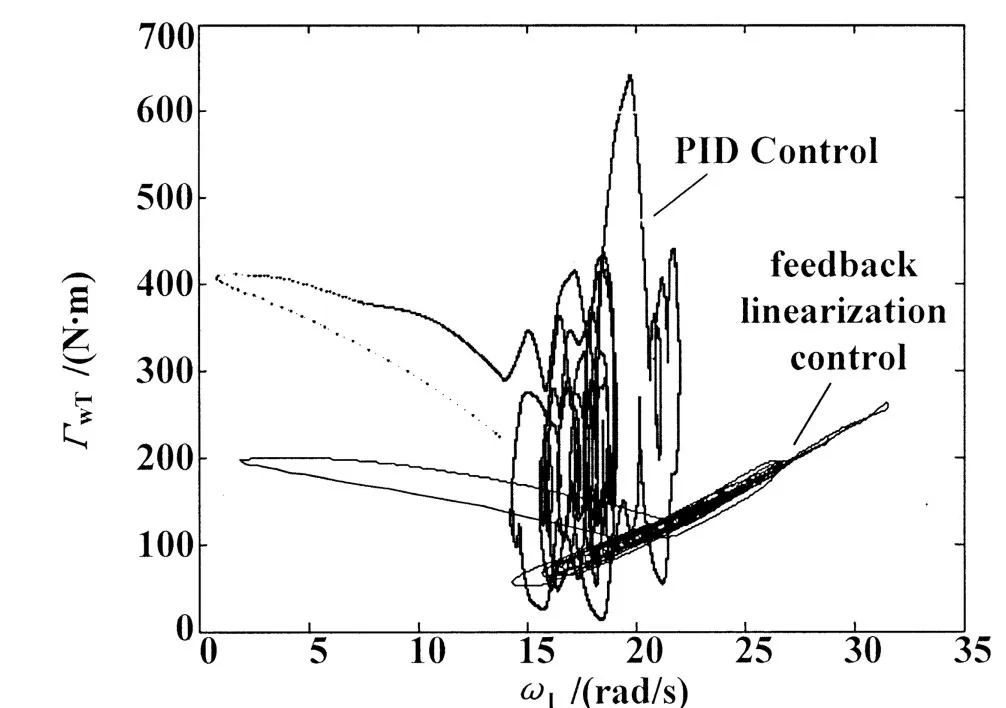
图10 转矩跟踪特性曲线比较
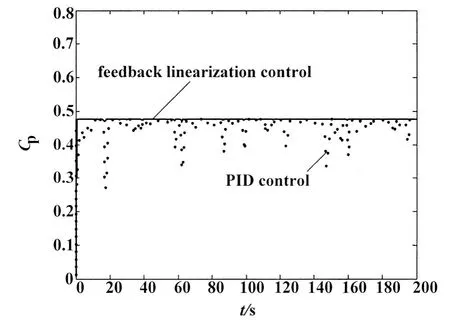
图9 功率系数曲线比较
[1] BIANCHI F D,DE BATTISTE H,MANTZ R J.Wind Turbine control systems [M].London: Springer,2007,60-160.
[2] MUNTEANU I,BRARCU A I,CUTULULIS N A,et al.Optimal control of wind energy systems[M].Lon⁃don:Springer,2008,40-80.
[3]汪洋.基于永磁同步电机的风力机模拟技术研究[J].电机与控制应用,2011,38(9):41-45.
[4]吴凤娇,王卫玉,商玉娟,等.永磁同步电机的混沌模型及其控制器设计[J].机电工程技术,2013(12):34-36.
[5]王宝石,谷彩连.大功率直驱风力发电并网变流器主电路的研究[J].电机与控制应用,2012,39(3):44-47.
[6]张润和,刘永和,崔丽丽.永磁同步电动机伺服系统的直接反馈线性化控制[J].微特电机,2006(12):26-28.
[7]纪志成,冯海英,沈艳霞.基于反馈线性化的风轮机变桨距控制研究[J].微特电机,2011(11):40-43.
[8]刘栋良,严伟灿,赵光宙.基于转矩扰动估计的电机反馈线性化控制[J].电力自动化设备,2010(6):6-10.
[9]张涛,蒋静坪,张国宏.交流永磁同步电机伺服系统的线性化控制[J].中国电机工程学报,2001(6):40-43.
[10]孟涛,纪志成.风能转换系统双频环滑模控制[J].电机与控制学报,2009(11):152-156.
[11]李国庆,陈厚合,姜涛,等.基于微分代数模型的直流非线性附加控制[J].电力自动化设备,2012,31(6):34-38.
[12] 韩金刚,陈昆明,汤天浩.半直驱永磁同步风力发电系统建模与电流解耦控制研究[J].电力系统保护与控制,2012,40(10):110-115.
[13] 田友飞,李啸骢,徐俊华,等.变速恒频双馈风电机组最大风能捕获非线性控制策略[J].电力系统自动化,2012,35(11):27-32.

