低附带毁伤弹药的炸药/钨粉质量比对钨粉抛撒特性的影响

刘 俊,姚文进,郑 宇,李文彬,王晓鸣

(南京理工大学智能弹药技术国防重点学科实验室,江苏 南京 210094)

1 引 言

现代战争中,作战任务已经不再局限于对目标的大范围摧毁式的毁伤。在某些特殊的作战任务中,准确击中目标的同时,还要将毁伤控制在一定的范围内,保护附近无辜人员、设施。现代弹药精确制导化的程度越来越高,弹药的命中精度相应也得到较大幅度的提高,这就使得实现低附带毁伤成为可能[1]。

目前,国内,姚文进等[2-3]建立了钨粉杀伤元、非金属外壳、装药之间的关系模型,比较了相同外壳条件下钨粉与装药在三种不同比例结构组成时弹药爆炸后的超压威力特性,但是没有考虑炸药对钨粉的传热,对于粉末抛撒速度的研究也不够详细。王志芳等[4-5]对固体颗粒爆炸抛撒的近场阶段进行了理论研究,建立了固体颗粒抛撒速度、炸药爆热和装填比的理论关系式。国外学者[6-7]对于低附带弹药爆炸驱动惰性金属粉末的问题,重点放在了爆轰波和金属粉末相互作用期间的动量和热量传递上。但上述研究还仅限于实验和理论研究,低附带炸药/钨粉质量比对钨粉抛撒的数值仿真研究还未见报道。

本研究对姚文进建立的钨粉杀伤元与非金属外壳及装药之间的关系模型进行优化,把钨粉的热能也考虑在内,进一步完善理论模型。并对低附带弹药爆炸抛撒过程进行试验和数值仿真,得出不同质量比对钨粉抛撒速度的影响规律。

2 理论分析

由低附带毁伤弹药的作用原理[2-3]可知,该弹药对目标的毁伤作用主要依靠炸药的冲击波超压与钨粉的动能。高密度金属弹药爆炸后,炸药能量首先消耗在非金属复合材料弹壳的变形和破坏以及赋予钨粉的初始动能与热能上,余留部分才消耗在爆轰产物的膨胀和冲击波的形成上。因此,弹丸爆炸形成的空气冲击波比冲量要比无壳同等装药爆炸形成的冲击波比冲量弱,但是由于大量具有一定抛撒初速的钨粉还具有一定的比冲量,所以弹丸爆炸后的总比冲量非常大。因此,该弹丸爆炸形成混合场的比冲量要比传统杀爆弹爆炸形成的冲击波比冲量强,能够有效杀伤近场内目标。

根据能量守恒原理可知,炸药在爆炸过程中所释放的能量为[8]:

EB=Ek+E1+E2+Ea+Eb+Ef1+Ef2

(1)

式中,EB为炸药产生的总能量;Ek是破片动能(由于壳体是碳纤维复合材料,爆炸过程中已经燃烧殆尽,所以壳体的破片动能可以忽略不计);E1为爆轰产物的状态内能;E2为爆轰产物的动能;Ea为空气冲击波的能量(忽略不计);Eb为壳体的变形能(对于钢壳装药,壳体变形消耗的能量仅占总能量的1%～3%,由于碳纤维复合材料壳体比钢壳体更容易破碎,因此这部分壳体变形能可以忽略不计);Ef1为钨粉的动能;Ef2为钨粉的热能。

炸药的总能量为:

Eb=mQv

(2)

式中,m是炸药的质量,Qv为爆热。

爆轰产物的状态内能为:

(3)

式中,p为压强,V为爆轰产物的体积,γ为炸药的绝热指数,r0为壳体的内半径,r1为壳体破裂时的内半径(由材料的强度计算得到)。

爆轰产物的动能为:

(4)

钨粉动能为:

(5)

式中,vf0为钨粉的初速。

钨粉的热能为:

Ef2=cmfΔT=cmf(βT-T0)

(6)

式中,假设爆炸后所有粉末颗粒获得相同的温度,c是钨粉的比热容,T是炸药的爆温,T0是常温,取300 K,β是单个粉末颗粒的传热系数[9]。

(7)

式中,βVN是当σ→0的粉末颗粒传热系数,βCJ为当σ→,时的粉末颗粒传热系数(与炸药和粉末的选取有关),σ为粉末颗粒直径与炸药反应区长度之比,σ0、w是与粉末颗粒和炸药相关的系数。

将(2)到(6)项带入到(1)中,整理得:

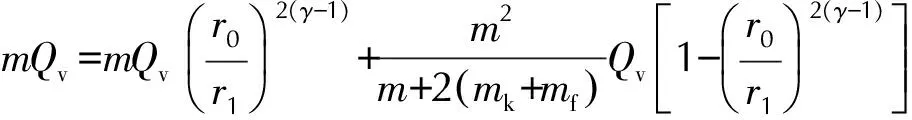
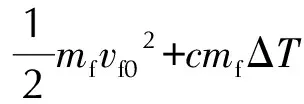
(8)

由式(8)可知,杀伤元的抛撒速度vf0主要取决于炸药质量m,钨粉质量mf和壳体质量mk三者之间的比例关系。计算中所采用的单位系统为：长度,m; 质量,kg; 时间,s; 温度,K; 导出单位：体积,m3; 压力,Pa; 速度,m·s-1; 爆热,kJ·kg-1; 动能与热能，kJ。

3 仿真模型及方案选取

在爆炸抛撒数值仿真中采用Lagrange方法[10]会形成严重的网格畸变,无法准确模拟粉末的抛撒过程,而光滑粒子动力学(Smoothed Particle Hydrodynamics,SPH)方法[11]是基于拉格朗日描述的无网格粒子方法,能较准确地模拟出粉末状态,因此本研究采用SPH和Lagrange耦合的方法来模拟爆炸抛撒过程。

本仿真计算时采用圆柱形战斗部,仿真中炸药和壳体采用Lagrange算法[10],钨粉采用SPH算法[11],如图1所示。战斗部参数：外壳材料为泡沫塑料,密度为1.265 g·cm-3,外径D=70 mm,内径d=60 mm,长度L=100 mm; 炸药采用Comp.B炸药,密度为1.717 g·cm-3,重金属粉末采用钨,密度为19.22 g·cm-3。壳体材料状态方程为SHOCK方程[12],无强度模型。Comp.B炸药选用JWL状态方程[13]。钨粉状态方程为SHOCK方程,由于钨粉是一种介于固相与气相的两相流材料,将它近似为一种没有强度模型的流体材料。为了节约计算资源,采用1/4三维空间模型。

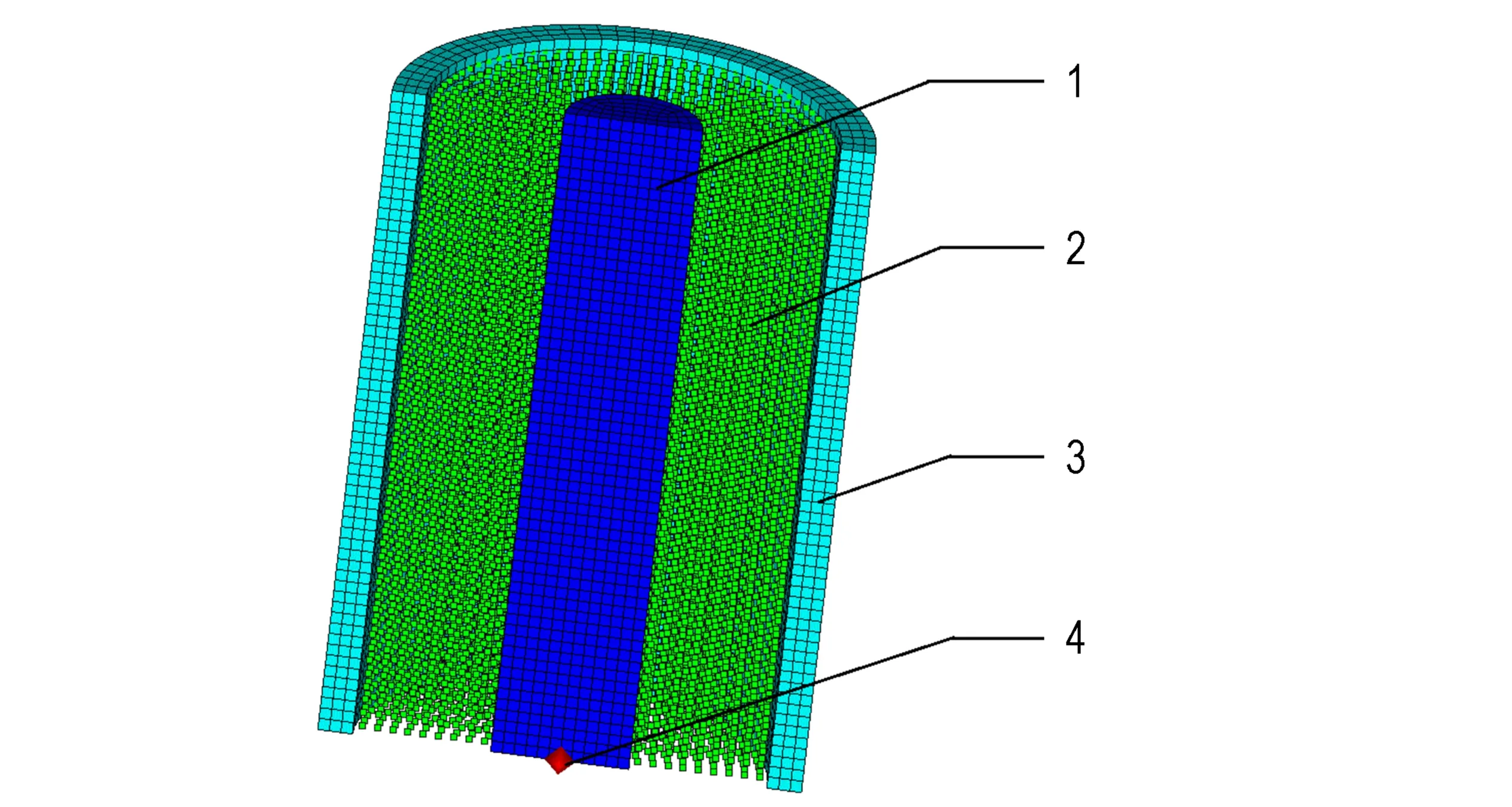
图1 战斗部数值仿真模型

1—B炸药,2—钨粉,3—壳体,4—起爆点
Fig.1 Numerical model of warhead

1—explosive,2—tungsten powder,3—shell,4—initiation point

为了明确炸药/钨粉质量比对钨粉抛撒速度的影响规律,参考文献[4]中的试验弹结构,壳体材料与尺寸保持不变,通过改变炸药/钨粉质量比,设计7种质量比方案进行仿真,见表1。

4 仿真结果与分析

4.1 炸药/钨粉质量比对钨粉抛撒半径的影响

低附带弹药爆炸过程可以简单分为3个阶段：加速、减速和湍流阶段。钨粉抛撒主要依靠加速和减速阶段。由于仿真只是为了得到炸药/钨粉质量比对钨粉抛撒初速的影响,本研究只关心炸药对钨粉驱动的初始几百微秒内的物理现象,所以只考虑钨粉加速阶段。此外,本仿真是一种理想真空状态,只考虑爆轰波对钨粉以及壳体的爆炸驱动作用。爆轰产物、钨粉、壳体与周围空气的作用都忽略不计。

表1 7种仿真方案的装药参数
Table 1 Seven simulation plans with different charge parameters

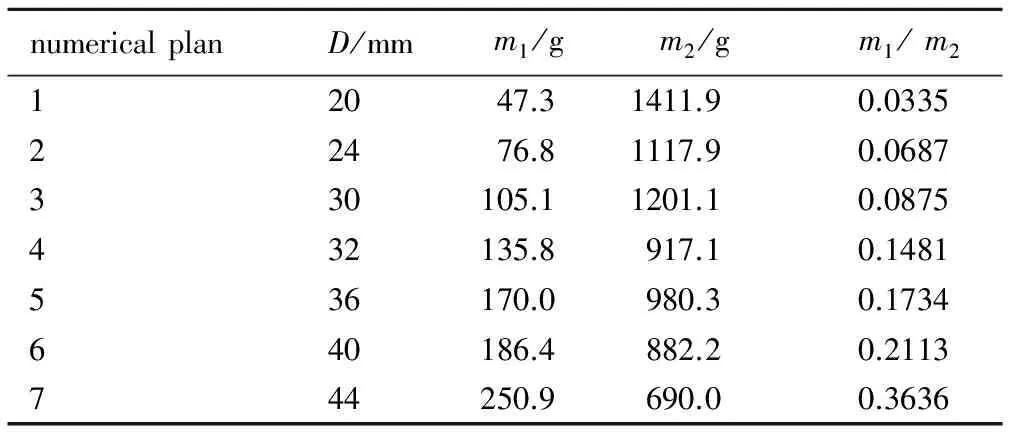
numericalplanD/mmm1/gm2/gm1/m212047．31411．90．033522476．81117．90．0687330105．11201．10．0875432135．8917．10．1481536170．0980．30．1734640186．4882．20．2113744250．9690．00．3636

Note：Dis charge diameter of explosive,m1is charge mass of explosive,m2is charge mass of tungsten powder,m1/m2is charge mass ratio between explosive and tungsten powder.

图2给出了7种方案300 μs时低附带弹药爆炸抛撒状态。从图2可以看出,不同炸药/钨粉质量比的粉末云都呈现轴对称椭圆形抛撒形态,中间的粉末云抛撒速度最高。由表2可以看出在300 μs下,从方案1到方案7质量比增加了8倍,钨粉抛撒半径增加了一倍多。

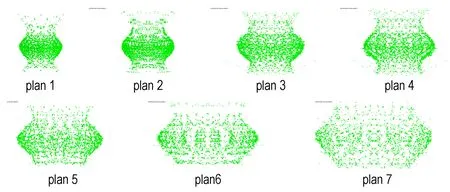
图2 7种仿真方案300 μs时钨粉抛撒状态
Fig.2 Dispersion state of tungsten powder under seven plans at 300 μs

表2 300 μs时7种仿真方案钨粉抛撒半径
Table 2 Dispersion radius of tungsten powder under seven plans at 300 μs

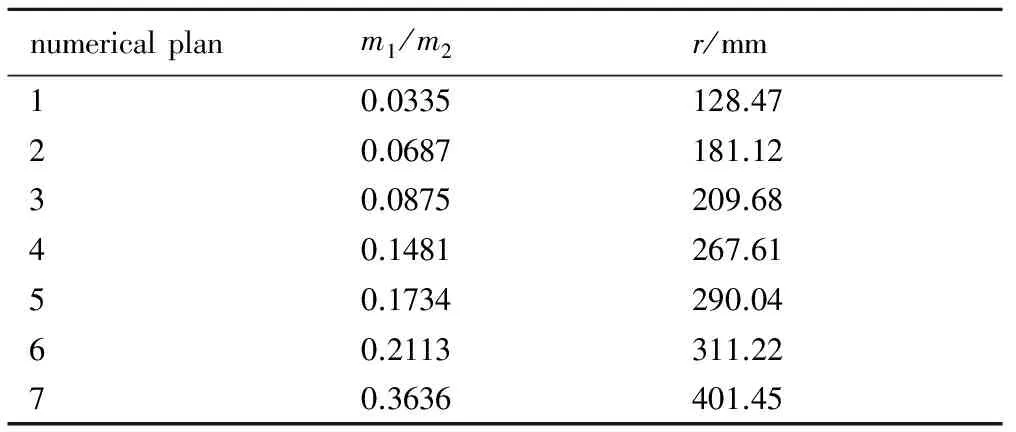
numericalplanm1/m2r/mm10．0335128．4720．0687181．1230．0875209．6840．1481267．6150．1734290．0460．2113311．2270．3636401．45

Note：ris dispersion radius of tungsten powder.

4.2 炸药/钨粉质量比对钨粉抛撒速度的影响

4.2.1 钨粉抛撒速度沿轴向分布规律

首先分析方案1的抛撒速度时间变化曲线。从0 mm处开始,选取轴向每隔10 mm处的共11个高斯点(速度观测点),观察它们的速度随时间的变化,见图3。从0 μs开始钨粉速度急剧增大,在10 μs左右形成一个速度峰值,之后出现一些波动,但是仍然缓慢上升,可以看出钨粉的速度在300 μs时趋于稳定。图4是7种方案的钨粉沿轴向第7个高斯点的速度时间曲线,可以看出其他6组钨粉速度随时间的变化趋势也大致如此,因此下面将选取300 μs时的速度进行分析。

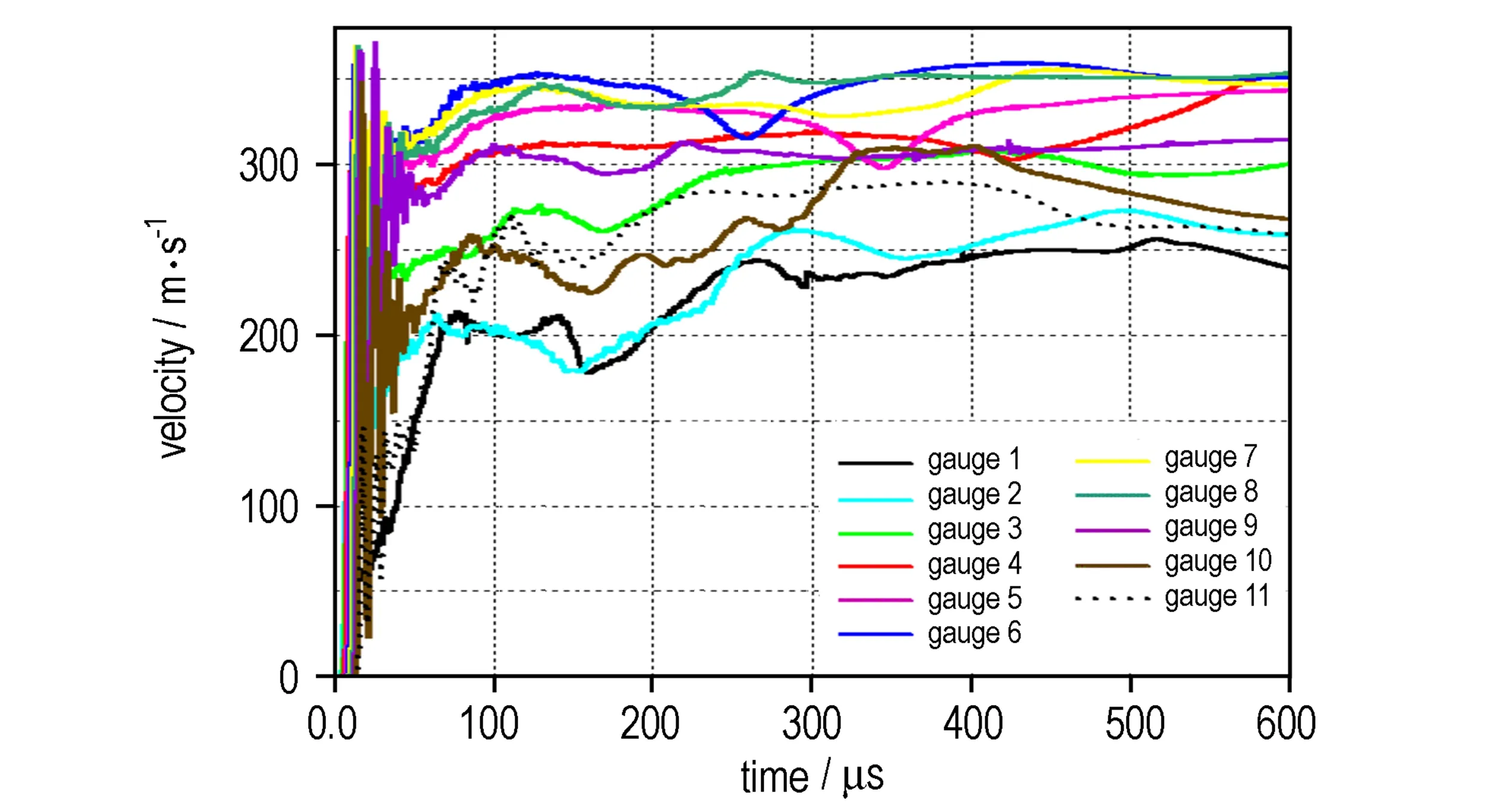
图3 方案1钨粉轴向速度随时间变化说
Fig.3 The axial velocity of tungsten powder varying with time under plan 1

图4 7种方案钨粉沿轴向速度随时间变化曲线
Fig.4 The axial velocity of tungsten powder varying with time under seven plans

以起爆点所在的面为高度基准面,统计7种方案在300 μs时速度沿轴向的分布,如图5所示。由图5可以看出随着高度的增加,钨粉的速度开始增大,在高度60 mm处,速度达到最大值,之后开始下降,最小速度出现在高度0 mm处。这主要是由于当一端起爆时,伴随着爆轰产物的膨胀,起爆端会先于另一端面泄压,高压区上移,最终会停留在中上端,然后爆轰产物开始沿径向扩散并驱动钨粉向外膨胀,因此本算例中钨粉沿轴向的最大速度出现在60 mm处。

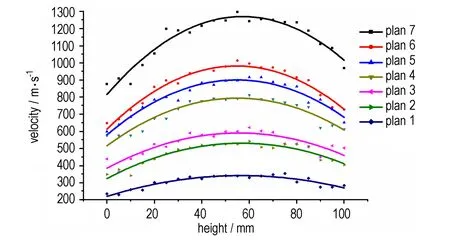
图5 不同质量比下钨粉抛撒速度沿轴向分布规律
Fig.5 The axial velocity dispersion of tungsten powder under seven plans with different charge mass ratio

4.2.3 炸药/钨粉质量比对钨粉抛撒速度的影响

从图5中可以看出随着炸药/钨粉质量比的增大,钨粉轴向抛撒速度分布曲线明显上升。并且轴向抛撒速度分布曲线上升的幅度也随质量比的增加而增加。当炸药/钨粉质量比为0.0335时(方案1),钨粉轴向抛撒速度分布曲线弯曲度较为平缓。然后随着质量比的提高,不仅整体沿轴向抛撒速度大幅提高,抛撒速度分布曲线弯曲呈度也开始加大。即随着质量比增大,同一发弹,钨粉沿轴向最大最小抛撒速度差距增大。例如,当质量比为0.0335时,最大抛撒速度与最小抛撒速度差为103.03 m·s-1。当炸药/钨粉质量比增大到0.3636时(方案7),速度差增大到420.5 m·s-1。

表3为不同质量比下钨粉的抛撒速度特性,沿轴向的最大抛撒速度即为钨粉抛撒初速。为了得出炸药/钨粉质量比对钨粉抛撒初速的影响规律,统计钨粉最大抛撒速度、钨粉平均速度与质量比的关系曲线,如图6。由图6可以看出,钨粉的最大抛撒速度和平均抛撒速度都与炸药/钨粉质量比呈非线性递增关系,但是钨粉的平均抛撒速度比钨粉最大抛撒速度低19.7%到31.5%左右。通过比较发现两曲线都有一个相同的特点,曲线斜率最初比较大,但是随着炸药/钨粉质量比增大逐渐变小。即当炸药/钨粉质量比从0.0335(方案1)增加到到0.1734(方案5)时,增大质量比可以有效地增大钨粉抛撒速度。但是当炸药/钨粉质量比超过0.1734后,对钨粉速度的提高作用就开始减小[14]。拟合得到炸药/钨粉质量比与钨粉抛撒初速在一定条件下的关系式:

式中,y为钨粉的抛撒初速,x为炸药与钨粉的质量比。

表3 7种方案不同炸药/钨粉质量比下钨粉速度特性
Table 3 Velocity characteristics of tungsten powder under seven plans with different charge mass ratio

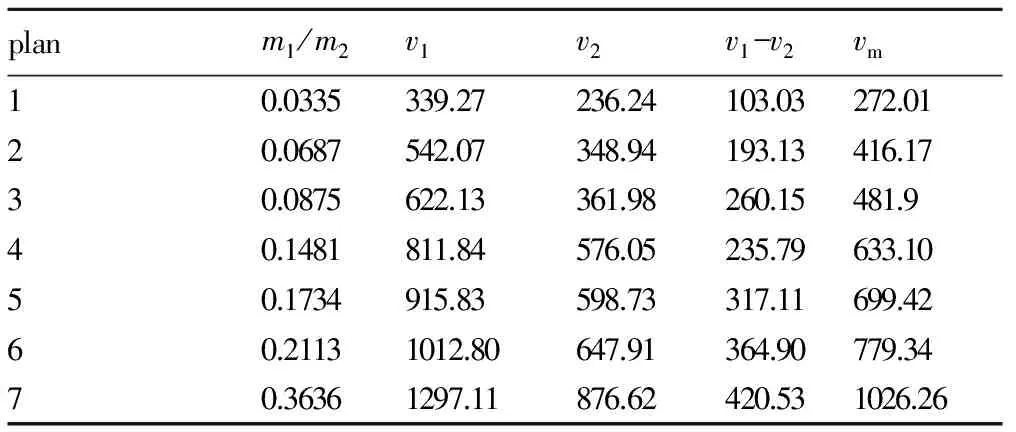
planm1/m2v1v2v1-v2vm10．0335339．27236．24103．03272．0120．0687542．07348．94193．13416．1730．0875622．13361．98260．15481．940．1481811．84576．05235．79633．1050．1734915．83598．73317．11699．4260．21131012．80647．91364．90779．3470．36361297．11876．62420．531026．26

Note：v1is the maximum dispersal velocity,v2is the minimum dispersal velocity,(v1-v2) is the velocity gap between maximum and minimum dispersal velocity.vmis the axial average dispersal velocity.

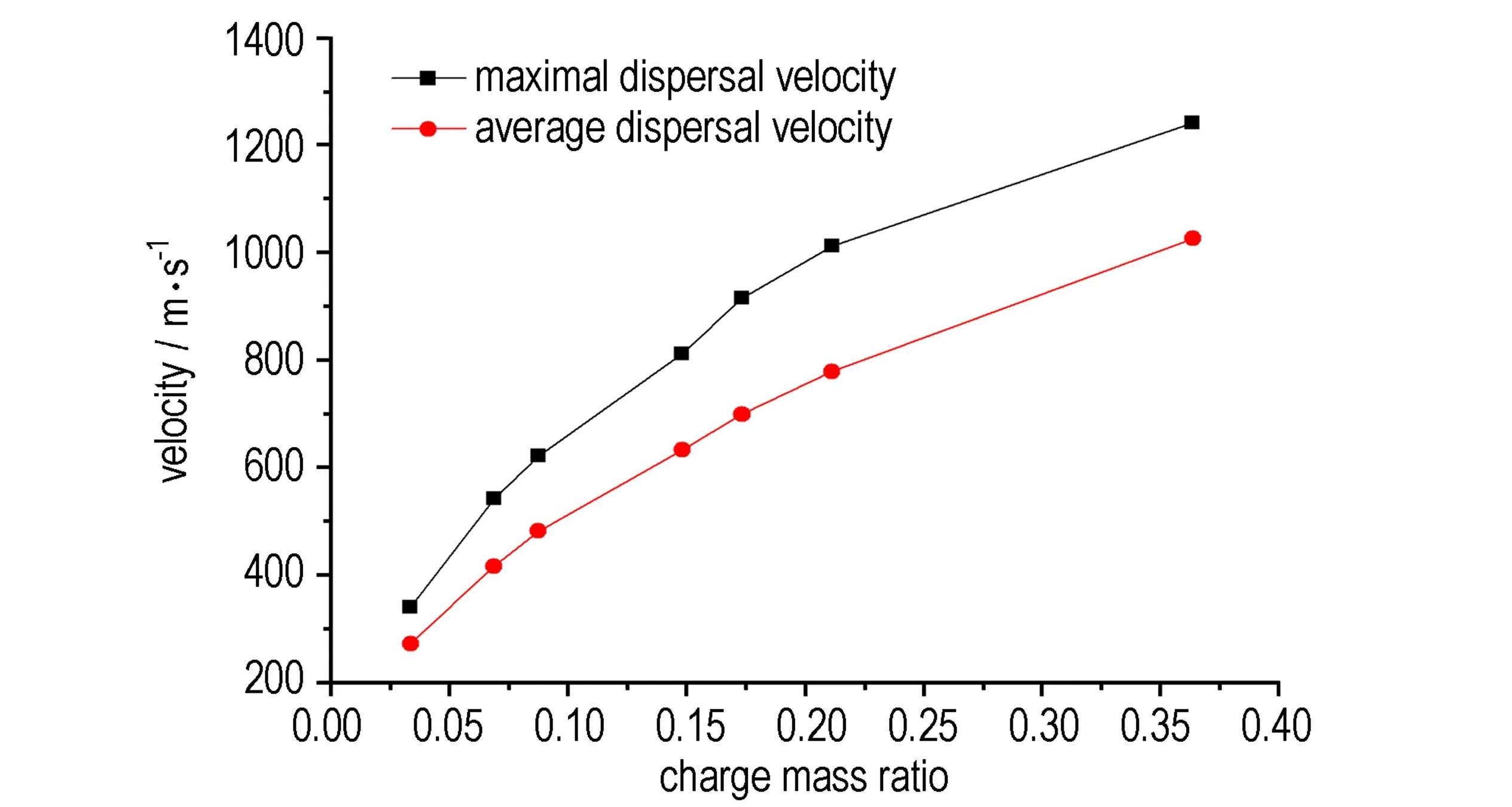
图6 不同炸药/钨粉质量比下钨粉的最大抛撒速度以及平均抛撒速度
Fig.6 Maximal and average dispersal velocity of tungsten powder under seven plans with different charge mass ratio

5 试验验证

5.1 试验布置

试验中采用柱形装药试验件,模拟弹内部装有钨粉。选用碳纤维复合材料作为壳体材料。壳体内径为60 mm,壁厚5 mm,长度100 mm。模拟弹采取一端中心起爆方式,选用B炸药作为主装药,装药密度为1.717 g·cm-3。为了验证炸药/钨粉质量比对钨粉抛撒速度的影响,并与仿真结果进行对比,本研究设计了3种不同质量比试验模拟弹。与仿真方案1,方案3,方案6相同,3种方案装药直径为20,30,40 mm,装填钨粉质量分别为1.4，1.2，0.88 kg,对应的炸药与钨粉质量比分别为0.0335，0.0875，0.2113。

图7为低附带静爆试验现场设备布置图,中心位置处放置一根木杆,其轴线垂直于水平面,木杆顶端固定一个木制的支架。模拟弹放置于水平支架上,模拟弹的底部距地面的高度为0.8 m。此外,为了记录炸药爆炸后钨粉的抛撒情况,在距离模拟弹20 m处架设一台彩色高速摄影机,拍摄速度为5000帧/秒。

图7 低附带模拟弹静爆试验现场布置图
Fig.7 Static explosion experiment layout of low collateral simulated projectile

5.2 试验结果分析

图8为炸药/钨粉质量比0.0335,0.0875,0.2113的模拟弹不同时刻的试验爆炸抛撒状态对比图。在试验照片中,单一的颗粒无法分辨,但是爆炸产生的粉末云团可以在照片中进行精确地标度,因此可以从高速摄影照片中清晰地看到爆轰产物的扰动以及钨粉颗粒在爆轰产物火球表面形成的大量均匀分布的规则射流。如果不考虑爆轰产物表面的不稳定的扰动,钨粉云看上去还是明显的围绕模拟弹的中心轴成轴对称椭圆状分布。这主要是由于气体爆轰产物膨胀(无论有没有钨粉存在),爆轰产物和周围空气之间的接触面发生扰动,服从泰勒不稳定性法则。另外可以发现同一时刻随着质量比的增大,钨粉的抛撒半径明显增大。根据高速摄影记录的图像,利用相关分析软件计算出3种质量比下钨粉的最大抛撒速度分别为278，580，1000 m·s-1。

a.m1/m2=0.0335

b.m1/m2=0.0875

c.m1/m2=0.2113

图8 3种炸药/钨粉质量比下各时刻钨粉的爆炸抛撒状态
Fig.8 Explosive dispersion state of tungsten powder at different moment for three charge mass ratios

将炸药/钨粉质量比、钨粉与B炸药相关参数带入公式(8)中,进行理论计算,绘出不同质量比与钨粉抛撒初速的关系曲线并与不同炸药/钨粉质量比下钨粉抛撒初速的数值仿真结果以及试验结果进行对比,如图9所示。可以看出,数值仿真、理论计算与试验结果趋势基本一致。这主要是由于数值仿真和理论计算是一种理想状态,没有考虑空气对能量的吸收,以及稀疏波和其他爆轰产物的影响。

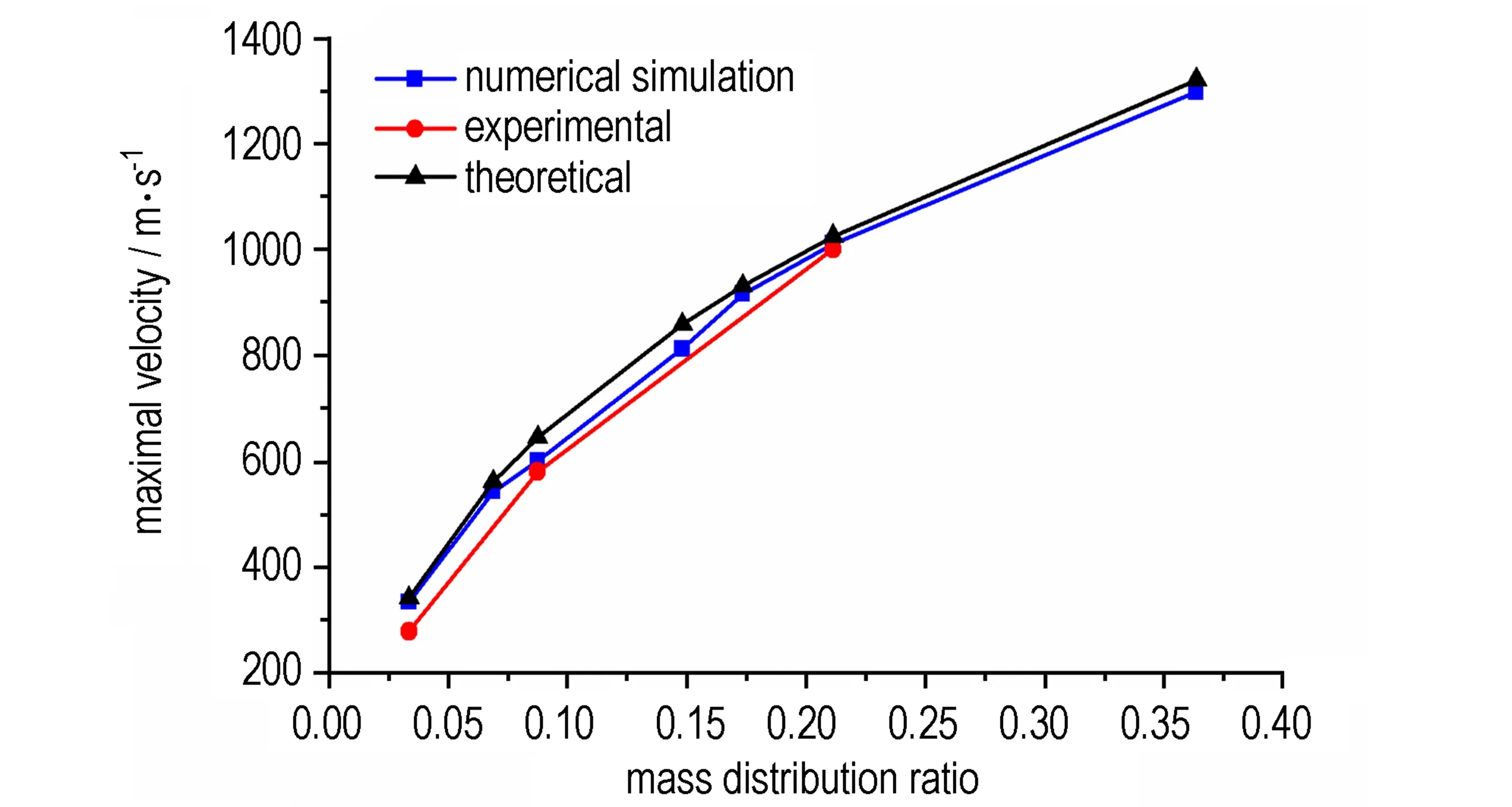
图9 钨粉抛撒初速仿真、理论计算与试验结果对比
Fig.9 Comparison of simulation,theoretical calculation and experimental results for initial dispersal velocity of tungsten powder

6 结 论

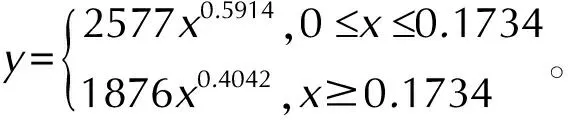
参考文献:

[1] 朱亮,低附带毁伤弹药设计及毁伤原理分析[D].南京：南京理工大学,2011：1-5.

ZHU Liang.Design and principle analysis of low collateral damage ammunition[D].Nanjing：Nanjing University of Science and Technology,2011：1-5.

[2] 姚文进,王晓鸣,李文彬.低附带毁伤弹药爆炸威力的理论分析与试验研究[J].火炸药学报,2009,32(2)：21-24.

YAO Wen-jin,WANG Xiao-ming,LI Wen-bin.Theory analysis and experiment research on blast effect of low collateral damage ammunition[J].ChineseJournalExplosivesandPropellants,2009,32(2)：21-24.

[3] 姚文进,王晓鸣,李文彬.高密度金属弹药组成比例对杀伤半径的影响[J].弹道学报,2010,22(2)：94-97.

YAO Wen-jin,WANG Xiao-ming,LI Wen-bin.Effect of configuration proportion of high-density metal ammunition on killing radius[J].JournalofBallistics,2010,22(2)：94-97.

[4] 王志芳,郑波.固体颗粒爆炸抛撒近场阶段的数值研究[C]∥中国力学学会学术大会,2005.

WANG Zhi-fang,ZHENG Bo.Numerical study of near-field explosive dispersal of solid particles[C]∥China mechanical Society Conference,2005.

[5] 王志芳,郑波.对固体颗粒爆炸抛撒的理论分析[C]∥中国力学学会学术大会,2005.

WANG Zhi-fang,ZHENG Bo.Theoretical analysis of explosive dispersal of solid particles[C]∥China Mechanical Society Conference,2005.

[6] Zhang F,Thibault P A.Momentum transfer during shock interaction with metal particle in condensed explosives[C]∥AIP Conference Proceedings,2002,620：934-937.

[7] Zhang F,Thibault P A.Shock interaction with solid particles in condensed matter and related momentum transfer[J].ProcRSocLondA,2003,459(2031)：705-726.

[8] 王儒策,赵国志.弹丸终点效应[M].北京：北京理工大学出版社,1993.

[9] Ripley,R C,Zhang F.Acceleration and heating of metal particle in condensed matter detonation[J].ProcRSocLondA,2012,468：1564-1590.

[10] 杨冬梅,王晓鸣.混凝土中爆炸数值仿真算法研究[J].爆炸与冲击,2003,25(6)：569-573.

YANG Dong-mei,WANG Xiao-ming.Study on numerical simulation method of explosion in concrete[J].ExplosionandShockWaves,2003,25(6)：569-573.

[11] 卞梁,王肖均,章杰.SPH/FEM耦合算法在陶瓷复合靶抗侵彻数值模拟中的应用[J].高压物理学报,2010,24(3)：161-167.

BIAN Liang,WANG Xiao-jun,ZHANG Jie.Numerical simulations of anti-penetration of confined ceramic targets by SPH/FEM couping method[J].ChineseJournalofHighPressPhysics,2010,24(3)：161-167.

[12] 郑宇,王晓鸣,李文彬.模型参数对射流侵彻半无限靶板的影响研究[J].计算机仿真,2009,26(1)：39-42.

ZHENG Yu,WANG Xiao-ming,LI Wen-bin.The effect of finite element model parameters on jet penetration into semi-infinite target[J].ComputerSimulation,2009,26(1)：39-42.

[13] 赵铮,陶钢,杜长星.爆轰产物JWL状态方程应用研究[J].高压物理学报,2009,23(4)：277-282.

ZHAO Zheng,TAO Gang,DU Chang-xing.Application research on JWL equation of state of detonation product[J].ChineseJournalofHighPressPhysics,2009,23(4)：277-282.

[14] 黄德雨,王坚茹,陈智刚.炸药配比对陶瓷低附带毁伤战斗部能量输出的影响[J].弾箭与制导,2012,32(1)：108-130.

HUANG De-yu,WANG Jian-ru,CHEN Zhi-gang.Influence of explosive radio on energy output of ceramic low collateral damage warhead[J].JournalofProjectiles,Rockets,MissilesandGuidance,2012,32(1)：108-130.