爆炸驱动燃料抛散的非理想化特征

史远通， 张 奇

(北京理工大学爆炸科学与技术国家重点实验室， 北京 100081)

1 引 言

燃料空气炸药(Fuel-Air-Explosive，FAE) 是一种高能燃料，本身不含氧，在特定起爆条件下可与空气中的氧反应，发生爆炸，形成云雾爆轰，具有与常规炸药不同的爆炸特性，主要应用于航空炸弹、火箭弹和导弹战斗部，作战效能显著，是一种低成本、多效能、面毁伤的新概念武器，世界各国的学者对此进行了大量的研究。

在FAE燃料的抛散方面，圣·路易法德研究所的M. Samirant[1]等人利用多种测试技术，研究了燃料的爆炸抛撒和FAE的形成过程； Glass[2]和Gardner[3]经过数值模拟分别得出云雾的扩展规律和近场的变化规律，并最终共同完成了远场和近场的耦合工作[4]；丁珏等[5]对燃料空气云雾形成过程进行数值模拟，并对抛散全过程编制程序，使预测云雾区内的物理参数成为可能； 张奇等[6]推导出了燃料在近区抛散初速度的计算公式，为燃料在近区的抛散建立了理论模型，同时通过建立力学模型[7]，分析了FAE装置壳体对燃料近区抛散的影响规律，给出了考虑壳体时燃料近区(加速阶段)抛散速度的计算方法,为FAE爆炸云雾及战斗部弹壳碎片的杀伤作用分析奠定了力学基础； 罗艾民等[8]推导出了燃料抛散距离的计算公式，使对燃料抛散半径的理论预测成为可能； 但以上工作均没有解决FAE试验和使用过程中频繁出现的“蹿火”问题。近年来的研究表明，采用不耦合装药的FAE装置在燃料抛散、控制中心装药的爆炸空腔、预防“蹿火”等方面存在着较大优势[9]，但在实际生产中，当中心装药采用不耦合装药时，中心装药的不耦合系数取多大合适，还没有学者进行研究； 同时，由于中心装药与中心管之间存在间隙，中心装药不可避免的会发生偏移，这是否会影响FAE效能的发挥，也非常值得探索。

基于此，本研究利用爆炸力学数值计算方法对FAE装置端部燃料的抛散、中心装药偏移对燃料抛散的影响及壳体局部弱化所造成的燃料抛散的非理想化特征进行了研究。

2 计算方法

计算采用LS-DYNA软件中的流固耦合算法[5]，网格边长控制在1 mm左右，最小网格尺寸为1 mm×1 mm×1 mm。计算时间为1500 μs，步长为0.6 μs。单元采用单点积分的ALE多物质单元，即一个单元内可以包含多种物质。炸药、燃料和空气区采用Euler网格，中心管及壳体采用Lagrange网格[9]，正确性验证同文献[9]。

3 材料模型及参数

空气采用MAT_NULL材料模型[10]以及用LINEAR_POLYNOMIAL状态方程[10]描述。线性状态方程为[10]：

p=c0+c1μ+c2μ2+c3μ3+(c4+c5μ+c6μ2)E(1)

计算中TNT炸药采用HIGH_EXPLOSIVE_BURN模型[11]，用EOS_JWL状态方程进行描述[11]：

(2)

式中，A1、B1、R1、R2、ω为与炸药性质有关的常数。E是单位体积炸药的内能，J·m-3;V是相对比体积，初始值为1。对于TNT炸药取A1=374 GPa;B1=7.33 GPa;R1=4.15;R2=0.90;ω=0.3;E=7.0×109J·m-3; TNT的密度为1650 kg·m-3; 爆速为6930 m·s-1[11]。

燃料采用MAT_NULL材料模型[12]和GRUNEISEN状态方程[12]描述, GRUNEISEN方程的具体形式如下[12]：

(3)

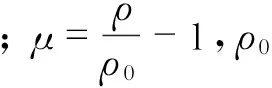
壳体材料为硬质聚氯乙烯(PVC)时，采用MAT_PLASTIC_KINEMATIC材料模型[7]，具体材料参数为：密度ρPVC=1300 kg·m-3; 抗拉强度σ=32MPa; 泊松比γ=0.38[7]。

壳体材料为钢时，采用HYDRO_SPALL模型[10]和GRUNEISEN状态方程[10]来描述，GRUNEISEN状态方程的形式同式(3)。钢材壳体的材料密度ρ钢=7.83×103kg·m-3; 剪切模量G=77 GPa; 泊松比0.3; 破坏应力或压力截弯取直值σ=900 MPa[10]。

4 中心装药对端部燃料的抛散作用

4.1 计算模型

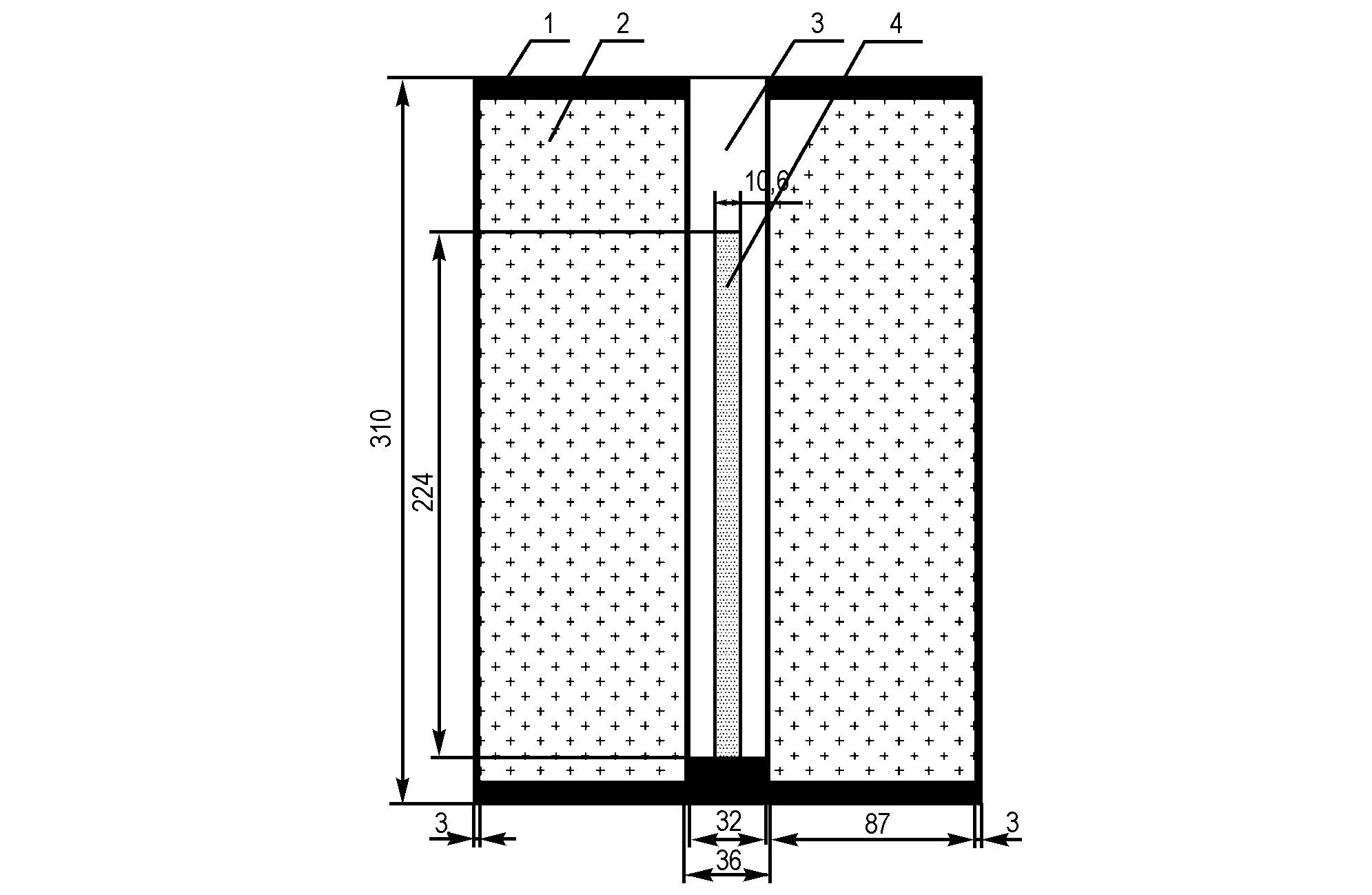
计算模型采取全尺寸模型进行计算。壳体外径216 mm，壳体内径210 mm，中心管外径36 mm，中心管内径32 mm，壳体高度为310 mm，上下端板厚10 mm，中心管壳体厚度为2 mm，外部壳体厚度为3 mm,壳体材料为硬质PVC。装药不耦合系数用De表示，耦合装药的情况下，De=1。1#模型采用耦合装药De=1, 2#模型采用不耦合装药De=2, 3#模型采用不耦合装药De=3。

a. 1#(De=1)b. 2#(De=2)

c. 3#(De=3)

图1 三种中心装药尺寸及结构(单位： mm)

1—壳体， 2—燃料， 3—空气， 4—中心装药

Fig.1 Structure of three kinds of center explosive charges(unit: mm)

1—shell, 2—fuel, 3—air, 4—center explosive charge

4.2 计算结果及分析

在观测点选取方面，观测点选在轴向(竖直方向)的1,2,29,30 cm，径向(水平方向)均选在最外层，结果如图2所示。

由图2可知,中心装药上端部燃料的抛散规律与对下端部燃料的抛散规律相反，采用不耦合系数为2的中心装药时，上下端部的燃料抛散速度最接近，形成的云雾更均匀，因此在中心装药的选择上，不耦合系数并非越大越好，而是存在一个最佳值。在本研究中,De=2最佳。

图2 不同中心装药情况下端部燃料的抛散速度变化规律

Fig.2 Dispersal velocity of fuel in ends of different center charges

5 中心装药(De=2)偏移对燃料抛散的影响

5.1 计算模型

FAE装置几何尺寸同4.1，壳体材料为硬质PVC。偏移尺寸分别为2,4,6,8 mm; 对应的偏移百分比为25%、50%、75%和100%。本研究将中心装药向左偏移定义为负偏移，对应方向定义为负方向; 向右偏移定义为正偏移，对应方向定义为正方向； 水平向左的燃料抛散速度用Vl表示，反之用Vr表示。中心装药不同负偏移情况下的模型平面示意图如图3所示。

a. 2 mmb. 4 mmc. 6 mmd. 8 mm

图3 中心装药不同负偏移情况下的模型平面示意图(单位：mm)

1—壳体， 2—燃料， 3—空气， 4—中心装药

Fig.3 Sketch of center charges with different negation offset(unit: mm)

1—shell, 2—fuel, 3—air, 4—center explosive charge

5.2 计算结果及分析

中心装药无偏移和偏移量为8 mm时的燃料抛散速度计算结果如图4所示。由图4可知，当中心装药偏移量为8 mm时，燃料抛散速度Vl的最大值为292 m·s-1，燃料抛散速度Vr的最大值为379 m·s-1，而无偏移时，燃料抛散速度的最大值为328 m·s-1，即中心装药偏移造成负方向燃料的抛散速度变小，而正方向燃料的抛散速度增大。

中心装药不同偏移情况下，燃料在正负方向的抛散速度最大值如图5所示。由图5可知，当中心装药负偏移量为2 mm时，负方向燃料抛散速度Vl的最大值为315 m·s-1, 与无偏移时相比较，减小13 m·s-1，在偏移量为8 mm时，负方向燃料抛散速度Vl的最大值为292 m·s-1，与无偏移时相比较，减小36 m·s-1; 而正方向的燃料抛散速度Vr的最大值在负偏移量为2 mm时为334 m·s-1,与无偏移时相比较，增大6 m·s-1,在负偏移量为8 mm时为379 m·s-1，与无偏移时相比较,增大51 m·s-1; 因而，当中心装药发生负偏移时，负方向的燃料抛散速度随着偏移量的增大而减小，而正方向的燃料抛散速度随着偏移量的增大而增大，即中心装药的偏移对FAE燃料的抛散有同向抑制，反向促进作用，且这种作用随着偏移量的增大而变得显著。产生上述现象的原因是当中心装药发生偏移时，中心装药两侧与中心管之间原本对称的间隙发生变化，这使得在中心装药起爆初期，爆炸所产生的高压气体更多的去填充偏移反方向的间隙，高压气体对两侧燃料产生了不均匀的推动作用，这种不均匀的推动作用，使FAE装置对称位置的燃料获得了不一致的抛散速度。当中心装药完全爆炸后，这种不均匀的推动作用消失。由于燃料获得了不一致的抛散速度，使燃料抛散的范围和均匀性以及燃料-空气浓度发生变化，影响FAE效能的发挥。

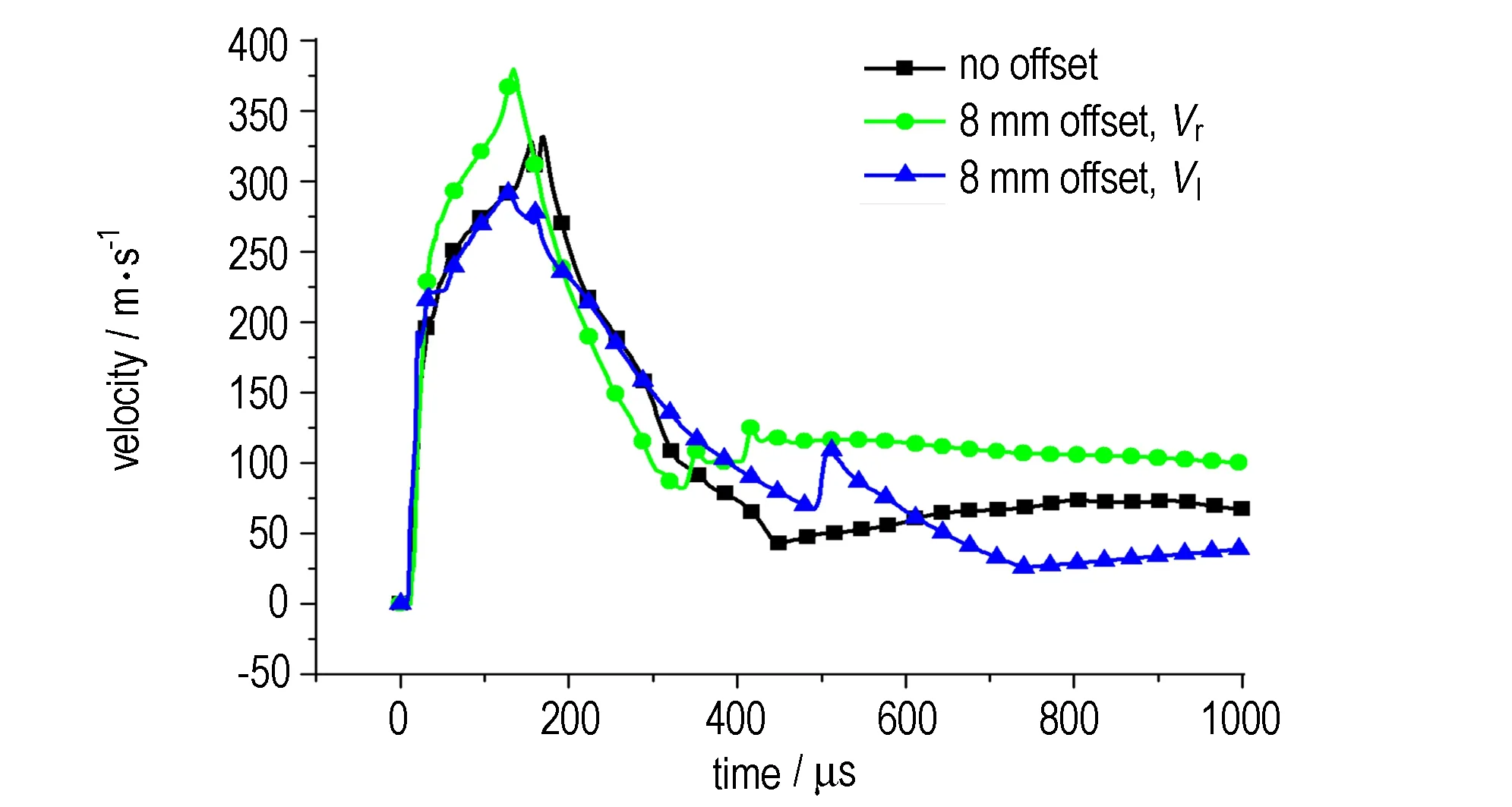
图4 中心装药不同偏移情况下燃料抛散速度

Fig.4 Dispersal velocity of center charge with different offset

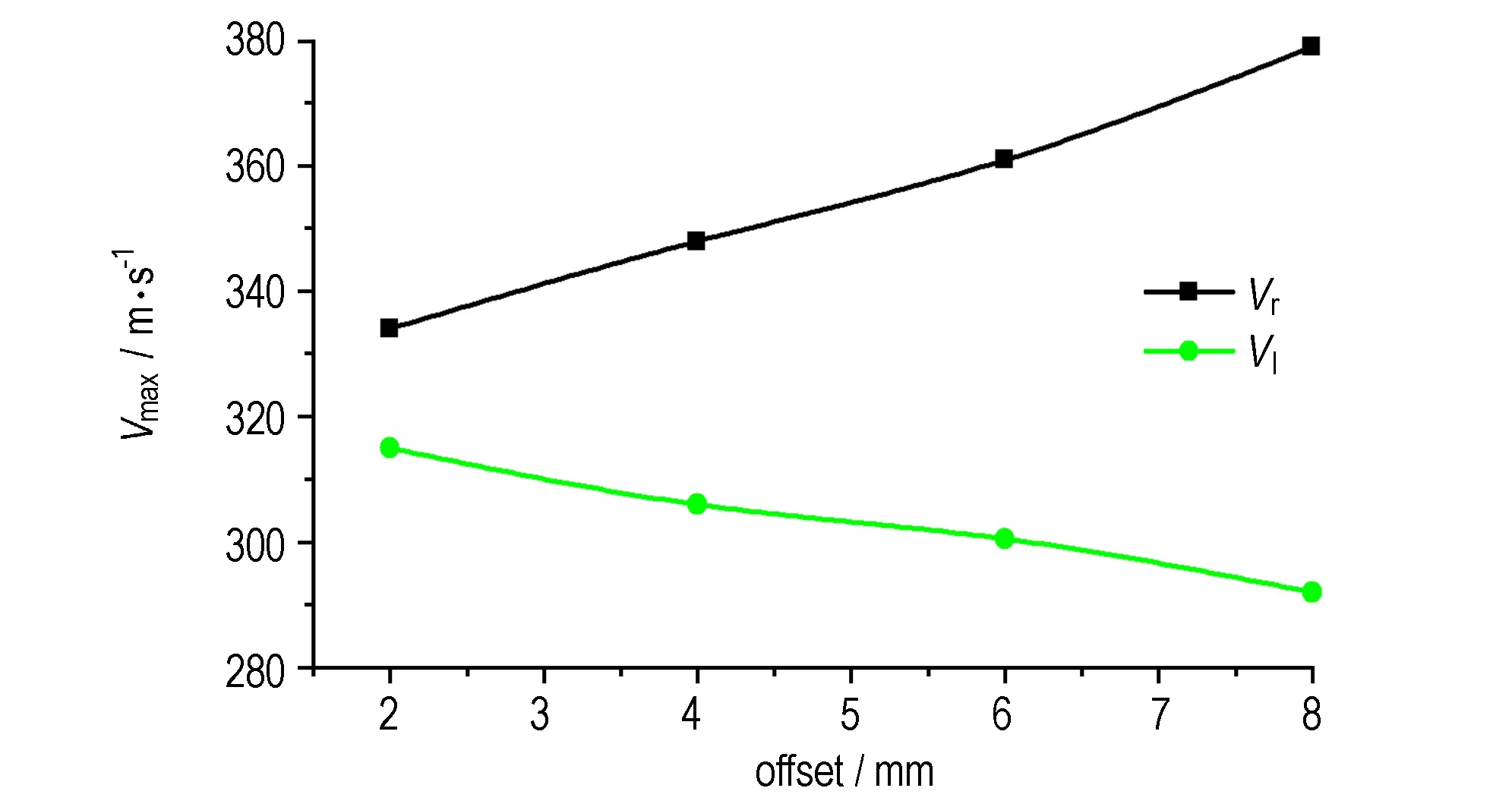
图5 燃料在正负方向抛散速度的最大值随中心装药偏移量的变化

Fig.5 Curves of maximum dispersal velocity of center charge changing with offset

6 壳体弱化引起燃料抛散的非对称性特征

6.1 计算模型

FAE装置几何尺寸同4.1。中心装药为采用耦合装药，在FAE装置右侧设置单侧弱化，弱化量分别为1 mm和2 mm，弱化后的壳体厚度分别为2 mm和1 mm，壳体料分别选取PVC和钢两种材料进行计算和分析。不同弱化情况下的FAE装置模型平面示意图如图6所示。

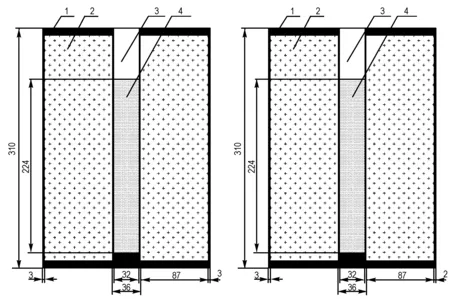
a. 2 no weakeningb. 1 mm weakening

c. 2 mm weakening

图6 壳体右侧不同弱化量情况下的模型平面示意图(单位： mm)

1—壳体， 2—燃料， 3—空气， 4—中心装药

Fig.6 Sketch of models with different weakening in the right side(unit: mm)

1—shell, 2—fuel, 3—air, 4—center explosive charge

6.2 计算结果及分析

采用PVC壳体的FAE装置在右侧无弱化和右侧弱化量为2 mm时，装置中部对称位置处燃料抛散速度随时间的变化趋势如图7所示。由图7可知，当PVC壳体单侧局部弱化量为2 mm时，弱化侧的速度Vr最大值为392.3 m·s-1，其对称侧的速度Vl最大值为397.8 m·s-1，而无弱化时的抛散速度最大值为412.5 m·s-1，即两侧燃料的最大抛散速度都有不同程度的降低，只是这种降低在弱化部位表现的突出，在其对称位置表现的不明显。

采用不同材质做壳体的FAE装置中部对称位置处燃料抛散速度的最大值随弱化量的变化如图8所示。由图8可知，当单侧弱化量为1 mm时，采用PVC壳体的FAE装置两侧燃料的抛散速度差值为5.5 m·s-1，同等条件下采用钢制壳体的FAE装置两侧燃料抛散速度的最大值差值为33.9 m·s-1; 当单侧弱化量为2 mm时，采用PVC壳体的FAE装置两侧燃料的抛散速度差值为8 m·s-1; 同等条件下采用钢制壳体的FAE装置两侧燃料抛散速度的最大值差值为45.5 m·s-1，这说明当单侧弱化现象出现时，速度的减小现象在使用PVC壳体(弱约束)时表现得轻微，在使用钢制壳体(强约束)时表现得显著。在武器系统的应用过程中，大多数FAE装置的壳体采用的是强约束(钢制壳体)，同时，由于二次起爆药包的安装，会使得FAE装置两侧的壳体厚度出现不均匀，造成燃料抛散速度的下降，进而影响其抛散半径及燃料空气浓度，最终影响FAE效能的发挥。所以，在生产、勤务工作中，应尽量避免壳体厚度不均匀情况的出现，以便于FAE发挥出最大效能。

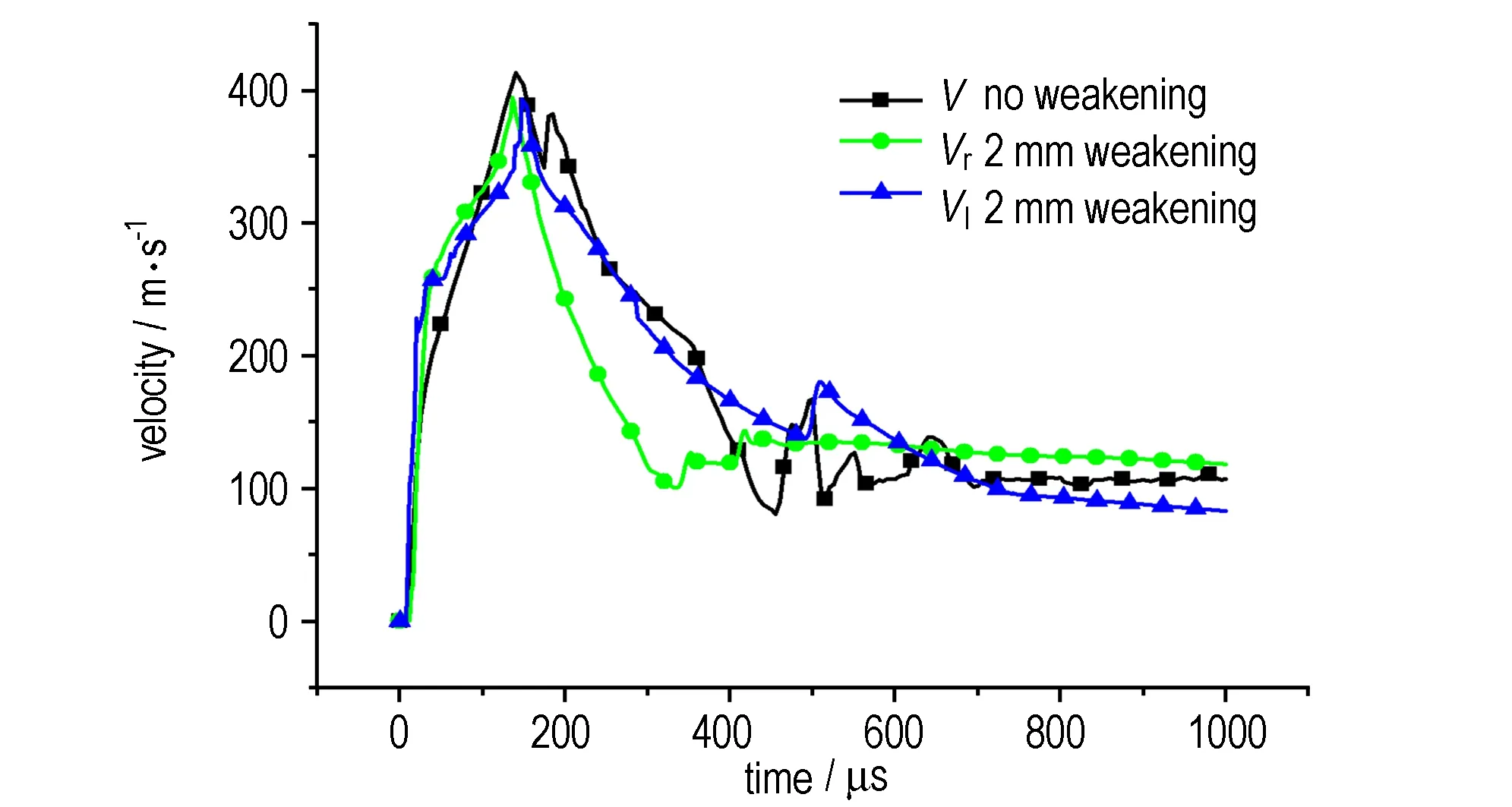
图7 装置中部对称位置处燃料抛散速度随时间的变化

Fig.7 The dispersal velocity in symmetry position of FAE devices changing with time

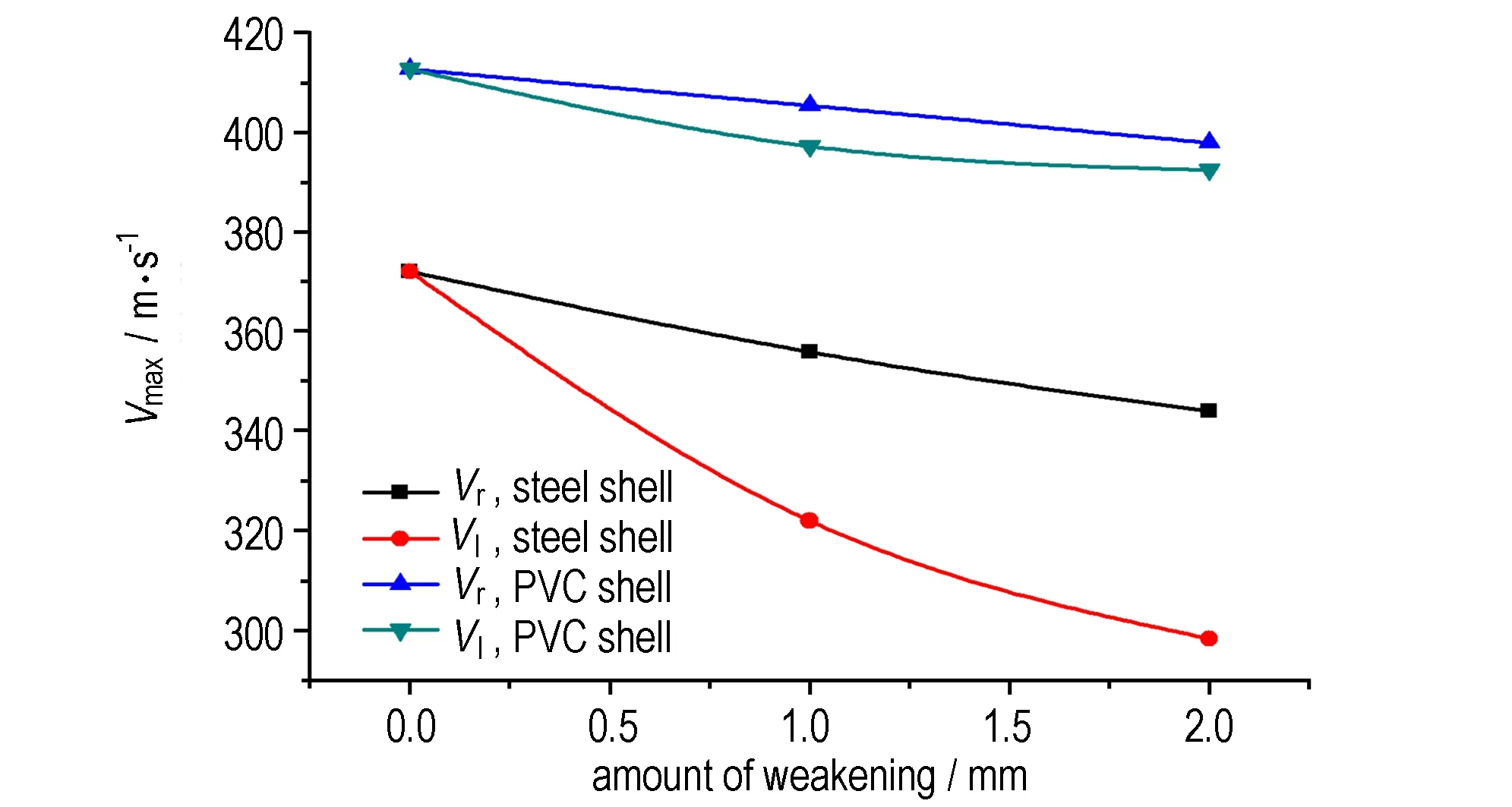
图8 FAE装置中部对称位置处燃料抛散速度的最大值随弱化量的变化

Fig.8 The maximum velocity in the middle of FAE devices changing with different offset

7 结论

(1) 中心装药采用不耦合装药时，不耦合系数并非越大越好，而是存在一个最佳值，在本研究中De=2时最佳。

(2) 中心装药负偏移量为2 mm时，负方向燃料抛散速度的最大值减小13 m·s-1，正方向燃料抛散速度的最大值增大6 m·s-1，负偏移量增大时，负方向抛散速度减小和正方向抛散速度增大的这种趋势更加明显，即中心装药的偏移对FAE燃料的抛散有同向抑制，反向促进作用，且这种作用随着随着偏移量的增大而增大。

(3) 当FAE装置壳体出现单侧弱化时，装置两侧燃料抛散速度的最大值都有不同程度的减小; 单侧弱化量为1 mm时，采用PVC壳体和采用钢制壳体的FAE装置两侧燃料的抛散速度差值分别为5.5 m·s-1和33.9 m·s-1，单侧弱化量增加为2 mm时，两者的差值则分别为8 m·s-1和45.5 m·s-1; 即速度减小的现象在使用PVC壳体(弱约束)时表现轻微，在使用钢制壳体(强约束)时表现显著。

参考文献:

[1] Samirant M，Smeets G，Baras C, et al. Dynamic measure in combustible and detonable aerosols[J].Propellants，Explosives，Pyrotechnics, 1989, 14: 47-56.

[2] Gardner D R. Near-field dispersal modeling for Fuel-air-explosive[R]. SAND 90-0686: 1990.

[3] Glass M W. Far-field dispersal modeling for Fuel-air-explosive[R]. SAND 90-0528: 1990.

[4] Gardner D R. Glass M W. A coupled near-field dispersal model for Fuel-air-explosive[R]. SAND 90-0687: 1990.

[5]丁珏,刘家骢.液体燃料爆炸抛散和FAE形成过程的数值仿真[J].南京理工大学学报,2000,24(2): 168-171.

DING Jue, LIU Jia-cong. Numerical study on the whole process of explosive dispersal for forming liquid-air cloud[J].JournalofNanjingUniversityofScienceandTechnology, 2000,24(2): 168-171.

[6] 张奇,白春华,刘庆明,等.不耦合装药爆炸作用下燃料空气炸药的近区抛散[J].弹道学报,2000,12(2): 22-25.

ZHANG Qi, BAI Chun-hua, LIU Qing-ming, et al. Near-field dispersal of FAE fuel under load of uncoupling charge in center pipe [J].JournalofBallistics,2000,12(2): 22-25.

[7] 张奇,白春华,刘庆明,等.壳体对燃料近区抛散速度的影响[J].应用力学学报,2000,17(3): 102-106.

ZHANG Qi, BAI Chun-hua, LIU Qing-ming, et al. Influence of shell casting on fuel near-field dispersal velocity [J].ChineseJournalofAppliedMechanics, 2000,17(3): 102-106.

[8]罗艾民, 张奇, 李建平, 等. 爆炸驱动下固体燃料分散过程的计算分析[J].北京理工大学学报,2005,25(2): 103-107.

LUO Ai-min, ZHANG Qi, LI Jian-ping, et al. Computational analysis of dispersion process of explosively driven solid fuel [J].JournalofBeijingInstituteofTechnology, 2005, 25(2): 103-107.

[9] 史远通, 张奇.中心装药对燃料抛散的影响及其空腔效应研究[J].含能材料,2014,22(3): 353-358.

SHI Yuan-tong, ZHANG, Qi. The research of center explosive charge for fuel dispersal and its cavity effect[J].ChineseJournalofEnergeticMaterials(HannengCailliao), 2014,22(3): 353-358.

[10] 王飞,白春华,闫华.壳体厚度对大口径FAE战斗部效应仿真研究[J].弹箭与制导学报,2003,28(3): 110-112.

WANG Fei, BAI Chun-hua, YAN Hua. The study for the effect of the thickness of cylindrical shell on the fuel dispersing in the FAE warhead design by simulation [J].JournalofProjectiles;Rockets;MissilesandGuidance,2003,28(3): 110-112.

[11] LSTC inc. LS-DYNA keyword user′s manual (Nonlinear dynamic analysis of structures, Version 960)[CP], May 2001.

[12] 辛春亮, 秦健, 徐更光, 等. 基于LS-DYNA软件的水下爆炸数值模拟研究[J].弹箭与制导学报,2007,28(3): 156-158.

XIN Chun-liang, QIN Jian, XU Geng-guang,et al. Research on UNDEX numerical simulation based on LS-DYNA [J].JournalofProjectiles;Rockets;MissilesandGuidance,2007,28(3): 156-158.