遗传算法在燃烧产物平衡组分计算中的应用

谢中元， 周 霖, 王 浩, 李守殿

(1. 西安近代化学研究所, 陕西 西安 710065； 2. 北京理工大学爆炸科学与技术国家重点实验室， 北京 100081； 3. 中国兵器工业规划研究院， 北京 100053)

1 引 言

燃烧产物平衡组分的准确计算是火炸药配方设计与性能预估的重要研究内容。目前，燃烧产物组分含量的计算方法主要有平衡常数法、最小自由能法等，其中最小自由能法由于不需要知道化学反应的中间过程且不涉及化学反应平衡常数的选取而应用最为广泛[1]，如美国国家航空和宇宙航行局采用最小自由能法计算了包含20种元素的燃烧产物组成[2]； 国内焦清介[3]、刘晶如[4]、庞维强[5]等应用最小自由能法计算了烟火药的燃烧产物组成，得到了与实验相符的结果。然而，最小自由能法求解过程中由于采用泰勒展开法、Newton法、布罗依登法[1]等方法对非线性方程组进行求解，其初始值设置难度增加，且对于多组分多相态的复杂的化学反应，其收敛也比较困难。

遗传算法是Holland J教授[6-7]提出的基于生物遗传和进化机制的适合于复杂系统优化的自适应概率优化计算方法，包含变量编码、复制、交叉、变异等过程，具有全局优化、操作简便以及较强的鲁棒性等特点，在单目标寻优、多目标寻优、参数优化、计划调度等方面具有广泛的应用。近年来，遗传算法逐渐开始应用于化学平衡计算，安维中[8]、潘功配[9]、贾冬梅[10]等应用遗传算法对含化学反应体系的相平衡进行求解，取得了良好效果。

基于遗传算法的优良特性以及火炸药的燃烧特性，本研究拟在最小自由能法的基础上引入遗传算法建立燃烧产物平衡组分计算方法，并以文献数据与实验测试结果验证计算结果的正确性。

2 计算模型

2.1 问题描述

热力学平衡理论[1]表明，当燃烧产物体系达到动态平衡时，自由能取得最小值，反之，当体系自由能达到最小值时，燃烧产物体系即为系统平衡体系，这就是最小自由能法求解燃烧产物平衡组分的基本原理。为表述清楚，设气态产物组分编号为1,2,…,N，固态产物的组分为N+1,N+2,…,M，则体系自由能G可表述为[9]：

(1)

(2)

(3)

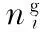
式(1)中气态燃烧产物与固态燃烧产物同时需满足以下约束条件：

(4)

式中，aij表示第i种燃烧产物中第j种元素的个数;Nj为火炸药配方体系中第j种元素的物质的量，mol;l为火炸药配方体系中元素的种类数。燃烧产物组分计算即在满足式(4)条件下，使得式(1)达到最小值时所求得的组分ni。

2.2 计算方法

计算按以下步骤进行： (1)根据变量数NVAR、种群大小NIND、变量字节数PRECI以及变量变化范围对基因编码; (2)计算目标函数值并将其作为初始值，进入包含适应度、选择、交叉、变异的循环计算，当条件满足时跳出计算; (3)输出计算结果。如图1所示。

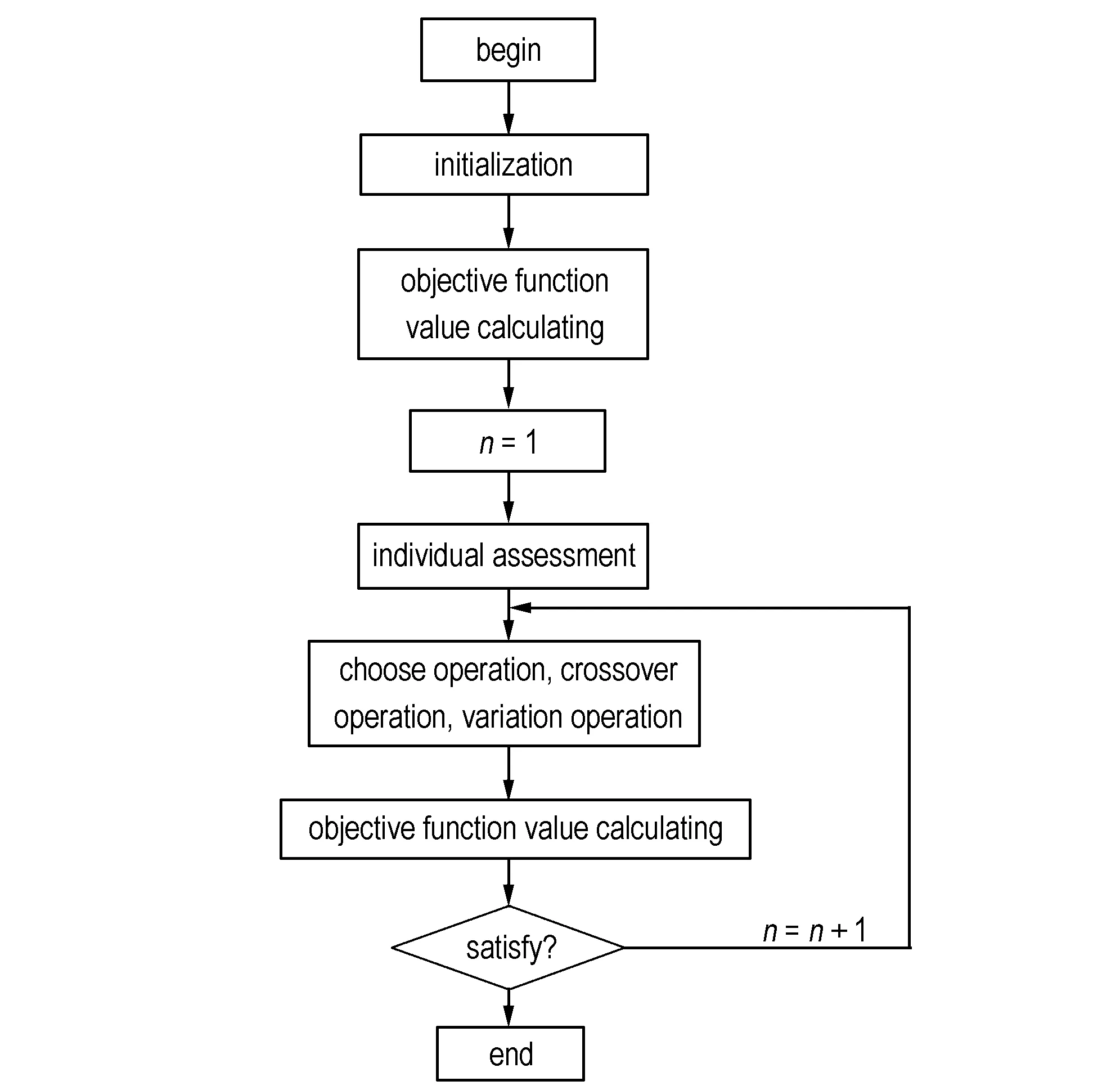
图1 遗传算法计算框图

Fig.1 Calculation flow chart of genetic algorithm

下面主要阐述遗传算法中自变量的选取与变化范围的确定、适应度函数的确定以及燃烧产物平衡组分计算方法。

2.2.1 自变量的选取与变化范围的确定

为叙述简便，以火炸药中应用广泛的CHON类化合物为例阐述自变量选取与变化范围确定的方法。

根据文献[1]中的研究结果，将1 kg CHON类化合物分子式表示为CaHbOcNd(下标表示化合物中相应元素的物质的量)，燃烧产物组分(14种)表示为：nC(solid)，nCO2，nCO，nCH4，nH2O，nH2，nH，nHO，nNH3，nN2，nN，nNO，nNO2，nO。鉴于各组分含量均满足约束条件，将式(4)展开为：

(5)

由于式(5)中包含4个线性化约束方程，因此可将4种组分表示为其它组分的线性关系式，进而使得独立燃烧产物组分变量由14个减少为10个，最小自由能函数(1)变为10个自变量的函数，且求解问题由线性化约束问题转化为线性化非约束问题。

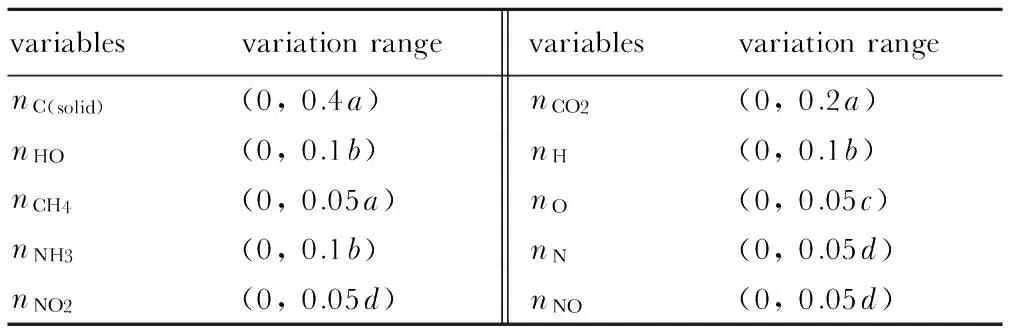
变量的选取与取值范围确定，原则上可以从燃烧产物中任取10种组分，只要这10种组分涵盖所有元素即可，但是由于各组分含量差异较大，任意选定的自变量不容易确定其变化范围。基于此，根据文献[1,3,11,12]，首先将上述14种燃烧产物组分分为两组，第一组为主要组分，包含nC(solid)、nCO2、nCO、nH2O、nH2、nN2，第二组为次要成分，包含nCH4、nH、nHO、nNH3、nN、nNO、nNO2、nO，其中，主要组分含量总和占燃烧产物总含量的95%以上; 然后根据次要组分含量少、变化范围小且容易确定等特点，选取包含不同元素的部分次要组分作为函数自变量，同时补充一定的主要成分作为自变量，本研究选取自变量为:nC(solid)，nCO2，nCH4，nH，nHO，nNH3，nN，nNO，nNO2，nO; 最后通过对文献[11]中火炸药燃烧产物组分含量的统计与整理，以较大上限确定各组分含量变化范围，如表1所示。

表1中a、b、c、d与CHON类化合物分子式下标相同。经计算表明，各变量的变化范围除nC(solid)和nCO2需要根据不同物质稍作调整外，其他变量的取值范围不需调节就可以满足不同化合物燃烧产物计算需求。显然，相对于泰勒展开法、Newton法以及布罗依登法[13]等方法对于空间点的初始值设置，本方法对少数自变量变化范围的确定要简便得多。

表1 变量取值范围

Table 1 The range of input variables

variablesvariationrangevariablesvariationrangenC(solid)(0,0.4a)nCO2(0,0.2a)nHO(0,0.1b)nH(0,0.1b)nCH4(0,0.05a)nO(0,0.05c)nNH3(0,0.1b)nN(0,0.05d)nNO2(0,0.05d)nNO(0,0.05d)

2.2.2 适应度函数确定

适应度是与目标函数值(体系自由能G)接近程度相对应的评价个体优劣的参数，越接近于目标函数值，则个体对应的适应度值越大，个体越容易继承。在Matlab遗传算法工具箱中是通过Ranking(ObjV)函数来计算个体适应度值的，其返回一个包含对应个体适应度的FitnV列向量。这个函数是从最小化方向对个体适应度进行排序的，即函数值越小，个体适应度越大，这正好与本研究的问题相吻合，因此可直接将目标函数(式(1))作为判别个体优劣的适应度函数。然而，Ranking函数是对正值数列进行求解的，而自由能为负值，因此，需要在最小自由能值前加上一个较大的正数使得最小自由能为正值，考虑实际计算情况，本研究增加的正数为2000。另外，由于各变量在其变化范围内是随机抽取的，因此很有可能出现组分含量为负值而不满足式(4)，为使其在迭代过程中被淘汰，需要设定一个大的数值使其适应度变小，本研究设定其为10000。适应度函数如式(6)所示，其中，“其它”是指燃烧产物组分含量为负值的情况。

(6)

2.2.3 燃烧产物平衡组分计算方法

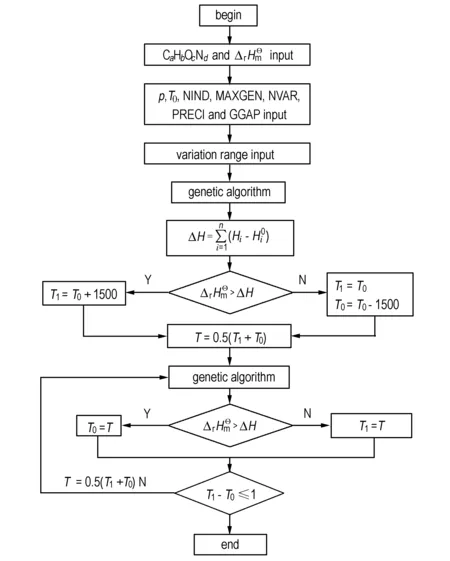
图2 总程序计算框图

Fig.2 Block diagram of the total calculation program

表2 输入变量

Table 2 Input variables

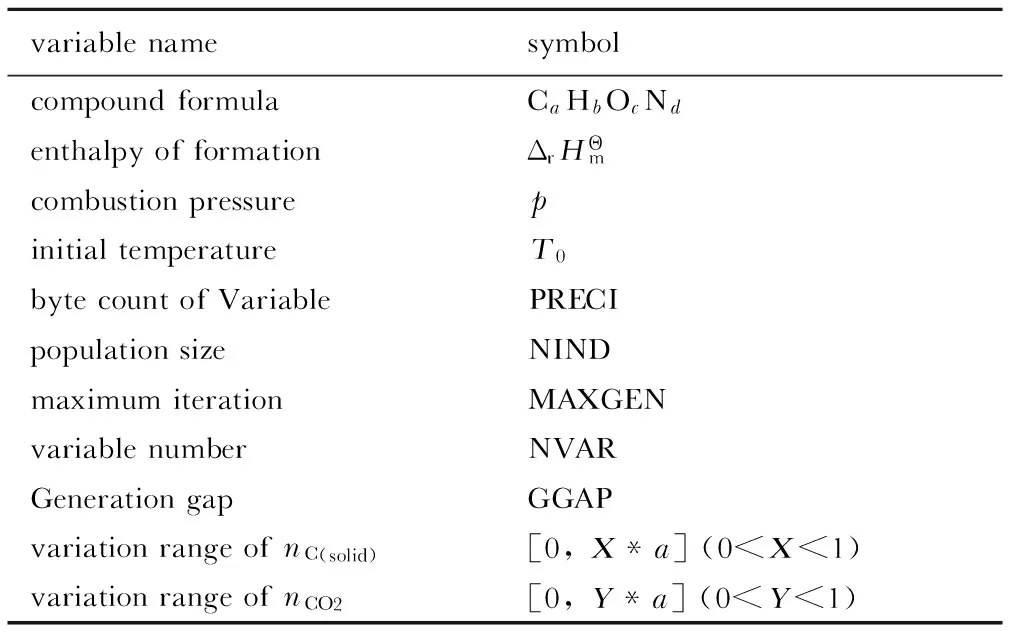
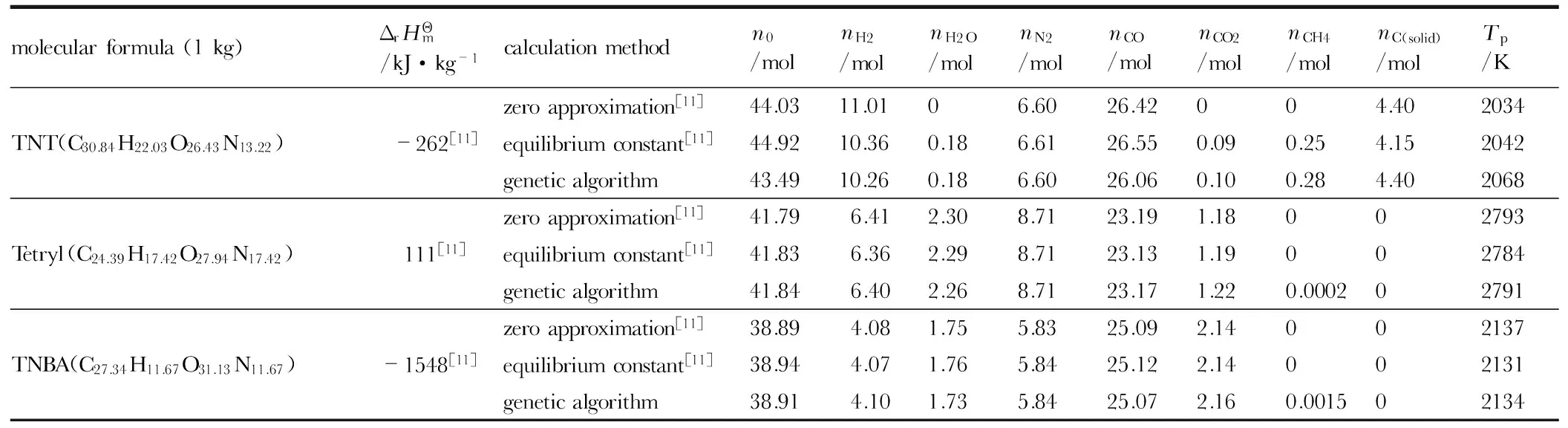
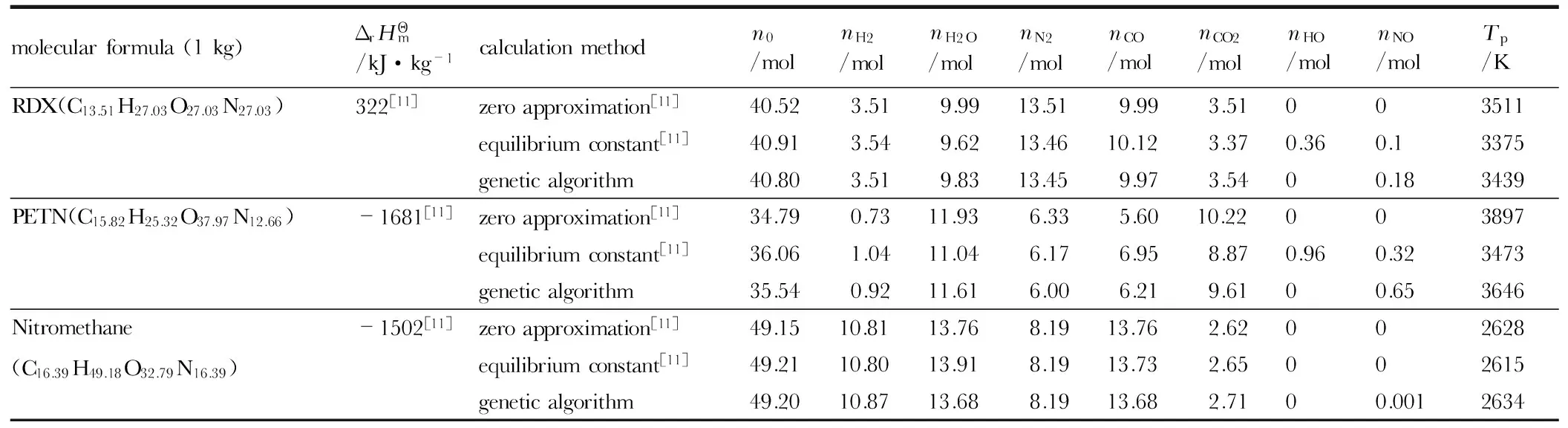
variablenamesymbolcompoundformulaCaHbOcNdenthalpyofformationΔrHΘmcombustionpressurepinitialtemperatureT0bytecountofVariablePRECIpopulationsizeNINDmaximumiterationMAXGENvariablenumberNVARGenerationgapGGAPvariationrangeofnC(solid)[0,X*a](0

表3 输出参数

Table 3 Output parameters

parameterssymbolisobariccombustiontemperatureTpcombustionheatQvmolenumberoftotalcombustionproductsn0molenumberofcombustionprod-uctsnC(solid),nCO2,nCO,nCH4,nH2O,nH2,nH,nHO,nNH3,nN2,nN,nNO,nNO2,nO

3 实例计算与分析

3.1 CHON类化合物燃烧产物平衡组分计算

为验证本方法的可行性及准确性，针对贫氧化合物(TNT，Tetryl，TNBA)与富氧化合物(RDX，PETN，Nitromethane)，采用本方法计算结果与文献[11]中零近似法、平衡常数法计算结果进行对比，结果如表4、表5，其中，燃烧产物压力均为30 MPa，变量数NVAR为10、种群大小NIND为200、变量字节数PRECI为20、最大迭代次数MAXGEN为3000、代沟GGAP为0.7、T0设置为3000 K、nC(solid)变化范围设置为[0, 0.4a]、nCO2变化范围设置为[0, 0.4a]。

从表4可以看出，针对贫氧化合物，零近似法计算、平衡常数法、遗传算法三者计算结果非常接近，但仍然存在一定的差别。其中，相对于TNT，nH2O与nCH4的平衡常数法计算结果分别为0.18,0.25 mol，而零近似法计算结果均为零，这是因为零近似计算法由于其自身假设与平衡常数法在微量元素计算方面存在较大的误差。遗传算法与平衡常数法计算结果基本吻合，组分含量误差在1%以内，温度误差在1.5%以内。

表5可以看出，针对富氧化合物，零近似法、平衡常数法、遗传算法三者计算结果存在一定差异。相对于PETN，零近似法与平衡常数法计算所得高含量组分nCO之间误差最高为20%，温度误差为12%; 平衡常数法与遗传算法计算所得高含量组分nCO2之间误差最大为7.7%，温度误差为4.9%。分析误差产生的原因在于: 零近似法是基于最大放热原则而提出的一种计算方法，当混合物体系为正氧平衡时，这种假设存在一定的不合理性从而导致计算结果误差较大; 而平衡常数法与遗传算法是基于化学动态平衡的两种不同形式而提出的计算方法，致使两者计算结果误差相对较少，另外，由于本方法只涉及到初始状态与最终状态，不受化学反应过程以及平衡参数的影响，因此计算结果更具可信性。

表4 贫氧化合物计算结果

Table 4 Combustion products of negative-oxygen compounds obtained by caculation

molecularformula(1kg)ΔrHΘm/kJ·kg-1calculationmethodn0/molnH2/molnH2O/molnN2/molnCO/molnCO2/molnCH4/molnC(solid)/molTp/Kzeroapproximation[11]44.0311.0106.6026.42004.402034TNT(C30.84H22.03O26.43N13.22)-262[11]equilibriumconstant[11]44.9210.360.186.6126.550.090.254.152042geneticalgorithm43.4910.260.186.6026.060.100.284.402068zeroapproximation[11]41.796.412.308.7123.191.18002793Tetryl(C24.39H17.42O27.94N17.42) 111[11]equilibriumconstant[11]41.836.362.298.7123.131.19002784geneticalgorithm41.846.402.268.7123.171.220.000202791zeroapproximation[11]38.894.081.755.8325.092.14002137TNBA(C27.34H11.67O31.13N11.67)-1548[11]equilibriumconstant[11]38.944.071.765.8425.122.14002131geneticalgorithm38.914.101.735.8425.072.160.001502134

表5 富氧化合物计算结果

Table 5 Combustion products of oxygen-enriched compounds obtained by caculation

molecularformula(1kg)ΔrHΘm/kJ·kg-1calculationmethodn0/molnH2/molnH2O/molnN2/molnCO/molnCO2/molnHO/molnNO/molTp/KRDX(C13.51H27.03O27.03N27.03)322[11]zeroapproximation[11]40.523.519.9913.519.993.51003511equilibriumconstant[11]40.913.549.6213.4610.123.370.360.13375geneticalgorithm40.803.519.8313.459.973.5400.183439PETN(C15.82H25.32O37.97N12.66)-1681[11]zeroapproximation[11]34.790.7311.936.335.6010.22003897equilibriumconstant[11]36.061.0411.046.176.958.870.960.323473geneticalgorithm35.540.9211.616.006.219.6100.653646Nitromethane(C16.39H49.18O32.79N16.39)-1502[11]zeroapproximation[11]49.1510.8113.768.1913.762.62002628equilibriumconstant[11]49.2110.8013.918.1913.732.65002615geneticalgorithm49.2010.8713.688.1913.682.7100.0012634

3.2 CHONAlClCs类推进剂热力学参数计算

爆热是表征推进剂热力学性能的重要参数，其数值大小与推进剂生成焓、燃烧产物组分含量等参数密切相关。基于此，针对于含CsNO3、铝粉的磁流体发电机专用推进剂配方[12]，本研究首先采用氧弹量热仪测试了不同CsNO3含量推进剂的爆热值，然后应用本计算方法对上述配方的爆热值进行计算，结果如表6所示。计算中各配方的生成焓由组分生成焓按含量加和得到，其它计算条件设置与2.1节相同。

表6可以看出，计算结果与实验结果呈现相同的变化趋势，随着CsNO3含量的增加，推进剂爆热逐渐降低; 计算结果与实验结果误差较少，当CsNO3含量为4%时，两者误差最大值为4.27%，表明本方法可用于含多种元素、多种固态物质的推进剂热力学参数以及燃烧产物组分含量的计算。

表6 推进剂配方及其性能

Table 6 Performance of propellants contained different CsNO3content

hydroxyl-terminatedpo-lybutadiene/%Di-n-octylsebacate/%toluenediisocyanate/%content/%AlAPCsNO3density/g·cm-3heat/kJ·kg-1testcalculationerror/%13.810.61864.621.78162076004.73.2613.810.61862.641.80261675903.44.2713.310.61861.161.81460805831.24.0913.810.61858.681.83058305769.51.0313.810.61856.6101.85158185658.62.74

4 结 论

(1)在最小自由能法的基础上，引入遗传算法建立了火炸药燃烧产物组分计算方法，并采用文献数据与含铯盐(CsNO3)推进剂实验测试数据验证了计算结果的正确性。

(2)相比于泰勒展开法、牛顿法等传统燃烧产物求解方法中严格的初始值设置要求，本研究建立的方法仅需确定少量组分的变化范围，计算过程难度降低。

(3)本研究建立的燃烧产物组分计算方法可适用于含C、H、O、N、Al、Cl、Cs等元素的复杂化学反应平衡体系的热力学参数以及燃烧产物组分含量的计算，具有精度高、计算简便等特点。

参考文献:

[1] 潘功配, 杨硕. 烟火学[M]. 北京:北京理工大学出版社, 1997: 42-52.

[2] White W B, Johnson S M, Dantzig G B. Chemical equilibrium in complex mixtures[J].TheJournalofChemicalPhysics, 1958, 28(5): 751-755.

[3] 崔庆忠，焦清介. 基于最小自由能原理设计黑火药组成[J]. 含能材料, 2004, 12(4): 214-217.

CUI Qing-zhong, JIAO Qing-jie. Design of the ingredients of black powder based on the least free-energy law[J].ChineseJournalofEnergeticMaterials(HannengCailiao), 2004, 12(4): 214-217.

[4] 刘晶如, 吕勇, 辛伟. 含能热塑性聚氨酯推进剂的能量计算与分析[J]. 固体火箭技术, 2012, 35(3): 376-381.

LIU Jing-ru, Lü Yong, XIN Wei. Calculation and analysis on energy characteristics of energetic thermoplastic polyurethane propellant[J].JournalofSolidRocketTechnology, 2012, 35(3): 376-381.

[5] 庞维强, 张晓宏, 樊学忠. 含Cs盐的HTPB/AP/Al复合推进剂特性研究[J]. 固体火箭技术, 2011, 34(5): 619-622.

PANG Wei-qiang, ZHANG Xiao-hong, FAN Xue-zhong. Study on properties of HTPB-based composite propellant with cesium salt[J].JournalofSolidRocketTechnology, 2011, 34(5): 619-622.

[6] Holland J H. Adaptation in natural and artificial systems [M]. Ann Arbor: University of Michigan Press, 1975.

[7] Montastruc L, Azzaro P C, Pibouleau L, et al. Use of genetic algorithms and gradient based optimization techniques for calcium phosphate precipitation[J].ChemicalEngineeringandProcessing, 2004, 43(10): 1289-1298.

[8] 安维中，胡仰栋，袁希钢．多相多组分化学平衡和相平衡计算的遗传算法[J]．化工学报，2003，54(5): 691-694．

AN Wei-zhong, HU Yang-dong, YUAN Xi-gang. Calculation of multiphase and multicomponent chemical equilibrium using genetic algorithm[J].JournalofChemicalIndustryandEngineering, 2003, 54(5): 691-694．

[9]范磊, 潘功配, 欧阳的华，等. 基于遗传算法结合支持向量机的Mg/PTFE贫氧推进剂配方优化[J]. 推进技术, 2012, 33(4): 620-624.

FAN Lei, PAN Gong-pei, OUYANG De-hua, et al. Application of genetic algorithm-support vector machine in formula optimization of Mg/PTFE fuel rich propellant [J].JournalofPropulsionTechnology, 2012, 33(4): 620-624.

[10] Jia D M, Deng W S. Phase and chemical equilibrium calculations by using of a hybrid method of the genetic algorithm[J].ComputersandAppliedChemistry, 2011, 28(9): 1175-1178.

[11] 周霖. 爆炸化学基础[M]. 北京:国防工业出版, 2005: 33-37.

[12] 周霖, 谢中元. 含Cs盐推进剂燃烧产物导电特性研究[J]. 含能材料, 2009. 17 (1): 99-102.

ZHOU Lin, XIE Zhong-yuan. Research on electrical conductivity of combustion production of composite propellant containing Cs salt[J].ChineseJournalofEnergeticMaterials(HannengCailiao), 2009, 17 (1): 99-102.

[13] 赵慕愚, 徐宝琨. 复杂化学平衡计算 [M]. 长春: 吉林大学出版社, 1990: 1-10.