批量伤（病）员急救中的护理人员优化分配

吴立晋，黄素芳，胡友珍，高小玲

批量伤（病）员往往突发性强、数量大、伤情复杂、危重病员多，在抢救过程中易造成混乱，多需紧急救治。明确批量伤（病）员岗位的职责，科学分配医务人员的任务，合理搭配人员，是保证医院高效率地抢救伤（病）员、提高伤（病）员救治成功率的重要措施。因此，批量伤（病）员抢救的人员调配问题成为医务界研究的重点和热点。目前，对批量伤（病）员抢救问题从制度、预案、方法等方面定性研究居多［1－6］，对医护人员的工作分配问题则缺乏定量计算，迫切需要引入运筹学方法更加科学地对人员定岗定位。鉴于这个目的，本研究运用匈牙利法［7］对批量伤员的工作进行优化分配，让合适的人做合适的事，提高医院整体救治效率。

1 匈牙利法的基本步骤

匈牙利法的原理是对一个效率矩阵进行等价变换，得到新效率矩阵，然后按照某种规则进行检验，如果不满足给定条件，对新效率矩阵继续进行等价变换，如此循环迭代，直到满足计算终止条件。其基本步骤如下：

第一步：使效率矩阵C经变换，在各行各列中都出现0元素。从效率矩阵的每行元素减去该行的最小元素；再从所得效率矩阵的每列元素中减去该列的最小元素。

第二步：标记0操作。遍历新效率矩阵的行，找到只含一个0元素的行，将该0元素画“O”；再遍历该0元素所在的列，将该列上的0元素画“/”。技大学同济医学院附属同济医院。

第三步：若画“O”的0的个数等于效率矩阵维数，则输出分配结果；否则，转入下一步。

第四步：用最少直线覆盖。①对没有画“O”0元素的行打√；②对已打√号的行中所有含画“/”0元素的列打√；③对打√列上有画“O”0元素的行打√号；④重复②、③直到得不出新的打√的行列为止；⑤打√的列画纵线，没打√的行画横线，这就是覆盖所有0元素的最少直线集合。

第五步：增加0元素。①求出未被直线覆盖的元素中的最小值k；②对打√行减去k，对打√列加上k。

重复第二、三、四、五步，直到画“O”的0的个数等于效率矩阵维数，输出分配结果。

2 批量伤（病）员抢救组的划分及任务

2.1 第一阶段：医院应急小组抢救准备 医师：由门岗通知医院应急小组相关专家到达急诊科，由急诊科主任或现场年资最高者分配专科教授每人负责一位病人，包括接诊、抢救直至病人分流至手术室或住院治疗。护士：急诊外科现值班人员，负责检伤、建档、急救物品准备、急救药品准备、急救区域划分、疏散现有留观病人等工作。其中，检伤按病情轻重程度分为病情危重（用红色标志）、病情较重（用黄色标志）、病情稳定（用绿色标志），急救区域划分为检伤区、A区（急救手术室、清创手术室）、B区（观察室）、C区（急诊外科输液室）、物资区、调度区。病情危重的伤（病）员一般安排在A区，病情较重的在B区，病情稳定的在C区。

在该阶段，由于护士的能力素质不同，完成各项任务的效率不同，为使急诊科的整体工作效率最高，需要让合适的人做合适的事。

2.2 第二阶段：医院整体抢救 医院立即成立指挥组、检伤组、急救组、手术抢救组、保障服务组、协调组、保卫治安组。所有应急急救工作在指挥组组长的指挥下，急救医疗由急诊科主任指导，护理工作由急诊科护士长安排，外来救援人员统一由急诊科调配，抢救疏散完毕，完成抢救记录，汇总抢救信息。

在该阶段，由于人力资源紧张，往往调配一个护士与一个医生搭档，对伤（病）员进行急救，为使急救效率最高，需要让合适的、配合默契的护士与医生协作。同时，各组人员内部也要进行合理分配任务，保证完成急救任务效率最高。

3 应急急救人员工作指派问题描述

3.1 第一阶段 在急诊科护士接到批量伤（病）员急救电话后，当班m名护士需要快速完成急救物品准备、急救药品准备、急救区域划分、疏散现有留观病人等n项工作。设第i（i＝1，2，…，m）名护士完成第j（j＝1，2，…n）项工作所花费时间的数学期望为cij（［cijn×n］称为效率矩阵C），若第i名护士做第j项工作，则令工作分配决策变量xij＝1，否则，若第i名护士不做第j项工作，则令xij＝0。

3.2 第二阶段 批量伤（病）员到达医院后，从其他科室调配I名护士增援，与急诊外科m名护士一起配合m＋l名医师进行急救。设第i（i＝1，2，…，m＋l）名护士与第j（j＝1，2，…，m＋l）名医师的配合默契度为cij，若第i名护士与第j名医师搭档，则令护士与医生搭档决策变量xij＝1，否则，若第i名护士不与第j名医师搭档，则令xij＝0。

以上阶段的指派问题经过变换，可以转换为标准指派问题，其数学模型如下：

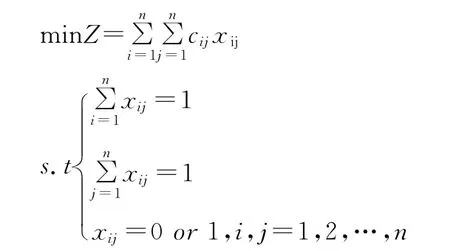
求解指派问题一般采用匈牙利法，具体步骤见下节。

4 具体应用

某医院实施交通事故批量伤（病）员急救，在第一阶段，急诊科有当班护士3名，分别用A1、A2、A3表示，需要完成电话通知相关科室和人员、急救物品准备、急救药品准备、急救区域划分、疏散现有留观病人5项工作，分别用B1、B2、B3、B4、B5表示，每名护士完成每项工作所花的时间（单位：min）见表1。为了在最短时间内完成急救准备，护士长根据实际情况，为每名护士安排一项或两项工作，求使总时间最短的指派方案。

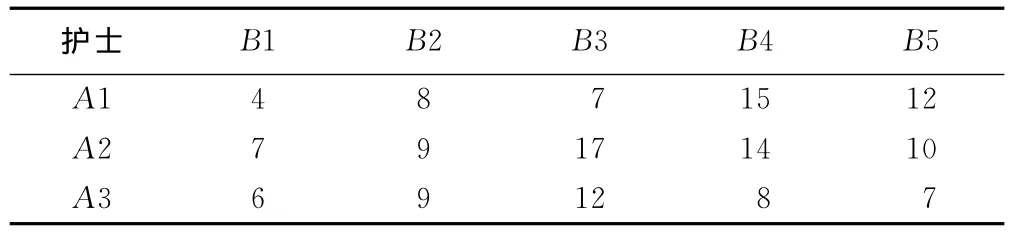
表1 每名护士完成不同工作所花费时间 min

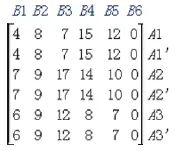
解：由于每名护士最多可以承担两项工作，因此可把每名护士看成两名护士，其效率矩阵为：

上面的系数矩阵有6行5列，为了使“人”和“事”的数目相同，引入一件虚拟的事B6，使之成为标准指派问题的系数矩阵：

然后，用匈牙利解法求解，得出决策矩阵：

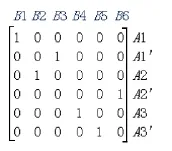
因此，工作分配方案为：护士A1对应做电话通知（B1）和急救药品准备（B3）两项工作，护士A2对应做急救物品准备工作（B2），护士A3对应做急救区域划分（B4）和疏散现有留观病人（B5）两项工作。

5 小结

本研究将运筹学方法运用于批量伤（病）员急救的人员分配，能根据医务人员的平时工作表现，结合人员信息档案的参考数据，运用匈牙利法对人员实施最合理的定岗定位，提高急救的整体效率，对医院的精细化管理具有一定的参考价值。

［1］陈晓松.现场急救学［M］.北京：人民卫生出版社，2009：2－3.

［2］邓艳华，陈达英，陈粹，等.合理人员调配对批量伤员救治效果的影响［J］.创伤外科杂志，2008，10（6）：488－489.

［3］王媛，宁丽欣，梁晓丽，等.护理应急预案在救治批量伤员中的应用［J］.中国误诊学杂志，2011，11（26）：6462－6463.

［4］吴学勇，张文治，聂永红，等.批量伤员院内急救组织与管理思考［J］.中国卫生质量管理，2011，18（4）：37－38.

［5］江琳，唐祖国.突发大批量伤员的院前急救分析［J］.基层医学论坛，2010，14（6）：195－196.

［6］宣善俊，杨芳，叶小兰.应急程序在批量烧伤伤员院前急救中的应用［J］.医学理论与实践，2012，25（18）：2264－2265.

［7］杨超.运筹学［M］.北京：科学出版社，2004：1.