高速铁路隧道及高架桥路段牵引网建模与分析

张桂南, 刘志刚, 郭晓旭, 高仕斌

(1. 西南交通大学 电气工程学院， 四川 成都 610031;2.铁道第三勘察设计院集团有限公司 电化电信工程设计研究处, 天津 300142)

牵引网作为牵引供电系统的重要组成部分，其性能直接影响牵引供电系统的供电可靠性。目前高速铁路普遍采用全并联AT供电方式，全并联AT供电方式下的牵引网结构复杂，包括上(下)行接触线T、承力索、正馈线F、钢轨R、保护线PW和贯通地线G等10余条线路；动车组通过隧道路段牵引网所处的电磁环境与明线区间存在差异；动车组通过高架桥路段牵引网的电路拓扑结构与明线区间线路也存在差异,表征出的电气特性也变得更为复杂，明线区间即为下文的普通路段。因而，对高速铁路普通、隧道、高架桥路段的牵引网开展相应数学模型和电气参数研究对掌握其电气性能具有重要意义。

针对电气化铁道AT供电方式牵引网复杂的拓扑结构，日本学者最先基于多导体传输理论建立了链式网络模型。随后国内外学者也进行了该模型的相关研究[1-3]，并基于该模型在基波潮流[4-6]、谐波潮流[7-8]、谐波谐振[9-11]等方面进行了广泛的研究工作，并取得了大量研究成果；然而，仍有一些问题值得关注：对于高速铁路牵引网复杂的多导体传输结构以及高速铁路存在的特殊路况，既有模型无法对复杂的电磁暂、稳态现象进行较好地研究和分析。

本文首先建立高铁全并联AT供电方式下的牵引网链式模型，推导多导线的阻抗及导纳矩阵计算公式；其次采用四周无限隧道模型计算隧道中导线的自阻抗、互阻抗和分布电容，结合电磁场理论研究高架桥路段牵引网电气参数；从而搭建各路段牵引网仿真模型。通过分析该模型输出电气量，得到与以往实验较为吻合的结果，证明了模型的准确性和可靠性。并在此基础上分析研究特殊路段的牵引网电压及钢轨电位的分布规律。

1 高速铁路牵引网数学模型

高速铁路全并联AT供电方式牵引网的各导线彼此平行分布，针对这种几何分布特性构成高铁链式网络电路：对牵引网进行特定长度切割，保证其分布参数特性，建立全并联AT供电方式下的牵引网链式网络模型。该链式网络模型由串联子网和并联支路2部分构成。通过牵引变电所、AT所、分区所、动车组形成的电流支路，将牵引网分割为若干个串联子网，在每个串联子网中又存在着并联支路，如牵引变压器、动车组、AT变压器、横连线等，见图1。图1中的平行多导体传输线构成子网的串联支路。以电流支路作断面向左右看去，可将每个子网的多根传输线用π型等效电路表示，从而将整个牵引网等效为链式网络，见图2。本文采用这种等效模型，建立了高速铁路牵引网数学模型。

图2中，V1～V5分别表示牵引网断面;Z(12)～Z(45)表示线路的等效阻抗;Y(12)～Y(45)分别表示线路的等效电导；断面1上Y(1)表示牵引变电所；断面2、4上I1、I2表示谐波电流源；断面3上YAT表示自耦变压器；断面5上Y(5)表示牵引网末端；断面间的平行多导线以π型电路进行等效。经网络划分，可将各支路阻抗及导纳用m×m阶矩阵表示，m为牵引网平行导体的数目[7]。假设将牵引网切割成N个部分，对其串联子网和并联支路适当建模，可得到它的总体链式网络形式，见图3。图中，Z1～ZN+1表示N个部分的线路阻抗;I1～IN+1表示N个部分的谐波电流源；Y1～YN+1表示N个截面上各部件的等效导纳。

2 牵引网特殊路段电气参数提取

目前高速铁路牵引供电系统建模中并未考虑高架桥、隧道路段的特殊性[12]，在精确性和可用性方面存在缺陷，因而对高铁牵引网特殊路段上电气参数的计算意义重大。

2.1 隧道中导线的电气参数计算

在研究处于地下深处的矿井隧道中导线自阻抗、互阻抗计算方法时，Tylavsky等人提出四周无限圆形隧道模型，并推导了隧道中导线的自阻抗、互阻抗公式[13-14]。图4为四周无限圆形隧道中的导线位置示意图，由图4可以看出隧道的断面近似为圆形，并且处于周围具有相同电阻率ρ、磁导率μ的大地深层。R为隧道截面圆半径；bi、bj为导线到圆心的距离；bij为两导线间的距离

式中：θ为两导线与圆心的夹角。

( 1 )

( 2 )

( 3 )

( 4 )

采用四周无限隧道模型，对高速铁路隧道导线电气参数进行求解，图5为隧道中的导线及其镜像。

图5中，i′、j′为两导线的镜像导线;Bi、Bj为镜像导线到圆心的距离；Dij、Dji分别为导线与另一条镜像导线间的距离。由于隧道内壁为等电位，无穷远处为零电位，设导线i的线电荷密度为τ，利用静电场镜像法，其镜像在它表面引起的电位为

( 5 )

在隧道内壁引起的电位为

( 6 )

导线j镜像在导线i的表面引起的电位为

( 7 )

隧道内壁实际上为电位参考点，式( 5 )和式( 7 )同时减去式( 6 )得

( 8 )

( 9 )

式中：ε0表示介电常数。根据多传输线线路的阻抗和导纳计算方法，得到导线的对地导纳Yii和两导线间的互导纳Yij。

2.2 高架桥上导线的电气参数计算

为保证线路运行的平顺性和安全性，高速铁路大量采用高架桥结构。桥梁的结构钢筋通常与贯通地线连接，相邻桥墩、贯通地线、大地形成局部闭合回路。该回路与桥上架空线供电回路间存在电气耦合，见图6。

由图6可知，架空线供电回路在相邻两个桥墩局部回路上产生的感应电流大小相等、方向相反，因此可以将它们等效为一个回路，如回路A，与此类似n个彼此相邻的桥墩即可等效为一个大回路[15]。根据能量守恒,有

(10)

式中：I为供电回路电流；R为每个桥墩的接地阻抗；M为牵引回路的耦合系数；R′为桥墩大回路的接地阻抗，该大回路与供电回路的耦合系数为nM，则有R′=nR；同理，若L为桥墩引下线的电感，L′为桥墩大回路的接地电感，则有L′=nL。

若将供电回路等效为无限长的回路，则其在桥墩大回路中产生的磁通量见图7。

根据电磁场理论，桥墩内磁通量可表示为

(11)

供电回路与桥墩回路的互感耦合系数为

(12)

式中：d1为接触网导高，d1=6.1 m；d2为桥梁高度，d2≈7 m；d为钢轨与贯通地线的垂直距离，d=0.4 m。将数据带入式(12)求得M=4.37×10-4H/km。两回路之间的互阻抗为Zm=jwM=j0.137 Ω，供电回路在桥墩回路中产生的感应电压为U=ZmI=0.137I。

3 牵引供电系统仿真分析

参照国内某条350 km/h客运专线，本文搭建的牵引网模型采用全并联AT供电模式，其牵引变压器由2 台单相变压器构成，它们的二次侧带中间抽头直接与钢轨连接[16]，省去牵引变电所内的AT。表1为变压器仿真参数。

表1 变压器参数

对牵引网进行建模，牵引网各导线空间分布见图8。牵引网导线的主要参数见表2[17]。图9为高速铁路某段隧道横截面图。

表2 牵引网导体的主要参数

利用上述实际线路参数及Cason理论，参照文献[5]对高铁普通、高架桥路段的牵引网的阻抗矩阵、分布电容矩阵等参数进行计算，(由于线路结构的复杂性，数据较多，故只列出上行各导线的相关参数)见表3、表6；结合2.1节理论分析，对高铁隧道路段的牵引网阻抗矩阵、分布电容矩阵等参数进行计算，见表4、表5。由于贯通地线深埋于地下或置于电缆槽内，它与其他架空导线间的互阻抗可忽略不计，故只求解它的自阻抗为0.305+j0.759。

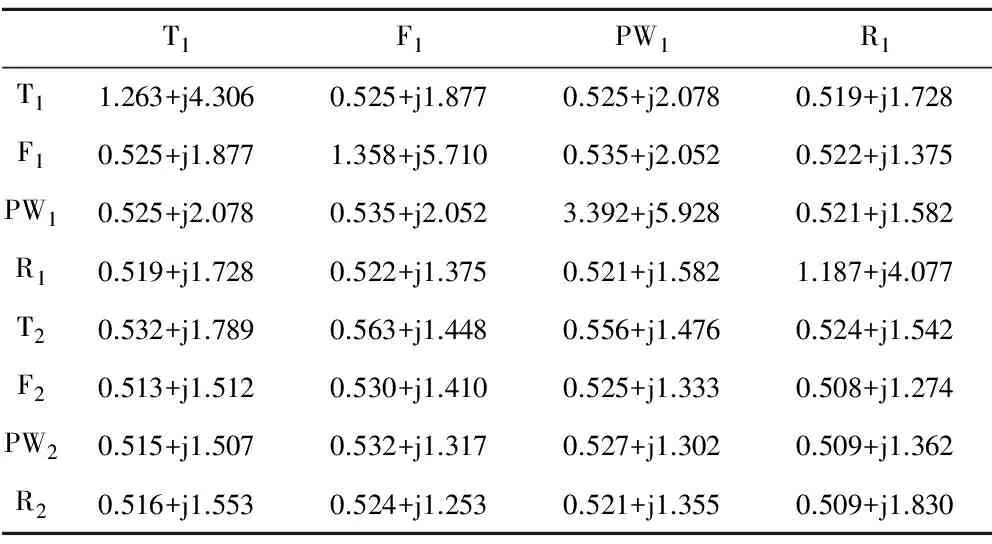
表3 高速铁路普通路段牵引网阻抗 10-1 Ω·km-1

表4 隧道路段牵引网阻抗 10-1 Ω·km-1

表5 高速铁路隧道路段牵引网分布电容 nF·km-1

表6 高速铁路高架桥路段牵引网分布电容 nF·km-1

注：T为C、J的合并，R为两条钢轨的合并。

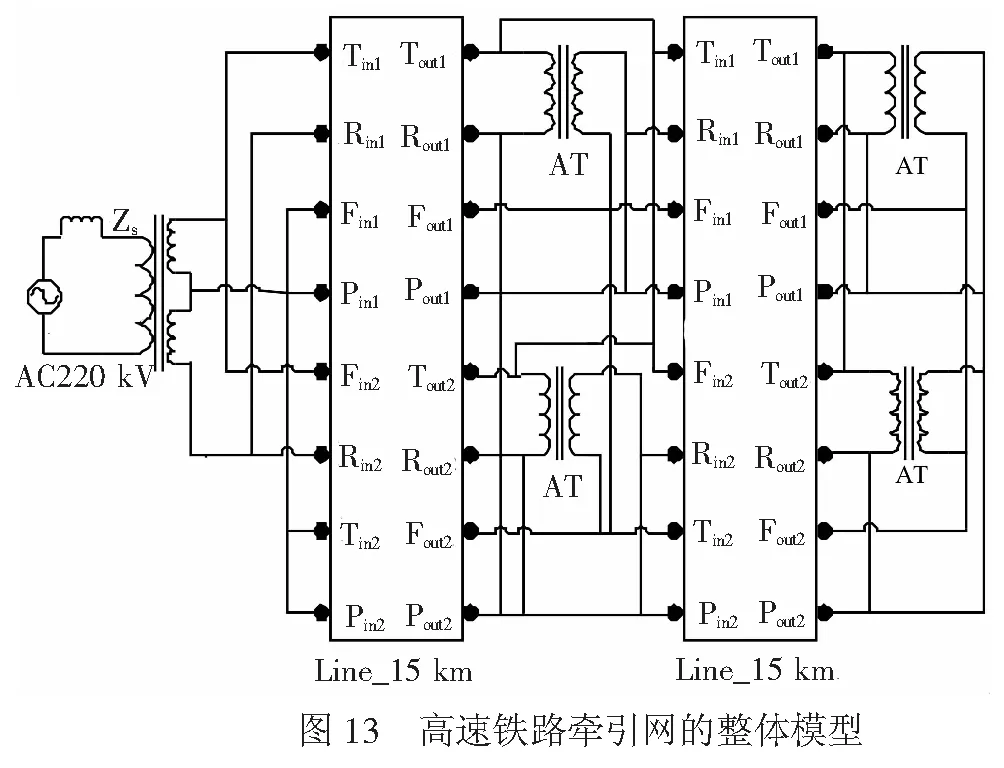
根据文献[18-19]的参数，在Simulink中用π型等效电路搭建切割后的子网模型，见图10。从图10中可以看出本文考虑了导线的自阻抗、互阻抗、对地电容以及分布电容。图11中，将每隔1 km的牵引网子网封装成1个模块，将其级联形成普通路段牵引网链式网络模型；黑色虚框内为高速铁路贯通地线阻抗的等效处理。由于隧道路段的链式网络模型的拓扑结构和普通路段相同，只是在导线的电气参数计算上存在差异。图12为5 km高架桥路段的链式网络模型，黑色虚框内为高架桥桥墩回路产生感应电压及桥墩对地阻抗。图13为本文搭建的完整的牵引网仿真模型。图10～图13中接触线、保护线、馈线及钢轨分别用T、P、F、R表示；电力系统侧变压器及线路的阻抗参数用Zs表示。

4 牵引网电气特性分析

为了更好地验证搭建模型的正确性，文中对比分析了高速铁路牵引网短路阻抗的理论计算值、仿真结果及所参照的客运专线实际测试值；此外，结合前人的研究和现场测试，文中分析了高速铁路各路段牵引网电压和钢轨电位的分布规律，再次对搭建模型的正确性给出相关验证。

4.1 牵引网短路阻抗计算及仿真

根据现场运行的全并联AT供电方式，设短路点到牵引变电所的距离为x，变电所到首个AT的距离为l1，首个AT到第二个AT的距离为l2。

当TR型故障发生在l1内时，短路阻抗为[20]

(13)

当TR故障发生在l2内时，短路阻抗为

Z=

(14)

当TF型故障发生在l1内时，短路阻抗为

(15)

当TF型故障发生在l2内时，短路阻抗为

(16)

TF型短路阻抗函数为开口向下的二次函数,且它们的极大值点分别位于各自的AT段内，因而当TR型故障发生在任一AT段内时，短路阻抗值都将随着故障点距离的增大呈现先增加后减小的分布趋势，即“马鞍形”短路阻抗特性曲线。分析TF型短路阻抗函数的极大值点对应的故障位置位于AT段外，因而将呈现连续增长趋势。

高速铁路牵引网普通路段、隧道路段以及高架桥路段TR、TF型短路阻抗仿真结果见图14。

图14中，TR、TF型短路故障阻抗特性曲线的分布规律与式(13)～式(16)的理论分析相吻合；此外，高架桥上的TR型短路阻抗值略高于普通路段，主要是由于钢筋结构的桥墩存在接地电阻。由于高架桥和普通路段的T、F线之间的牵引网拓扑结构没有变化，因此高架桥的TF型短路阻抗与普通路段基本一致。隧道路段TR、TF型短路阻抗均略低于高架桥和普通路段，是因为隧道路段的圆形结构与普通路段的半无限平面结构不同：线路回流时，电流集中分布在在回流点附近，整个回路的阻抗特性更多表征在距离导线较近的大地表层结构上，而隧道的圆形钢筋混凝土结构较大地的电阻率小，更易于大地中的返回电流能从四周流向导线。

为了验证仿真结果的正确性，与实际测试结果进行相关对比。工作人员在验收该客运专线某供电臂时，让距离AT所5 km处下行T线发生接地短路故障，编号213断路器动作，在变电所测得短路电流为3 986 A，网压为10.75 kV，短路阻抗为2.7 Ω。利用AT测距法测得故障位置为K241+69，距离换算后，故障实际发生在距离牵引变电所20 km处。从图14中可以看出，该位置的牵引网短路阻抗为2.61 Ω，与实测值仅有3.3%的相对误差。

以上理论、仿真以及实际结果对比分析表明，本文所搭建高速铁路普通、隧道及高架桥路段TR、TF型短路故障阻抗特性曲线的分布规律与理论分析相吻合，具备一定的合理性。

4.2 高速铁路牵引网电压和钢轨电位分布

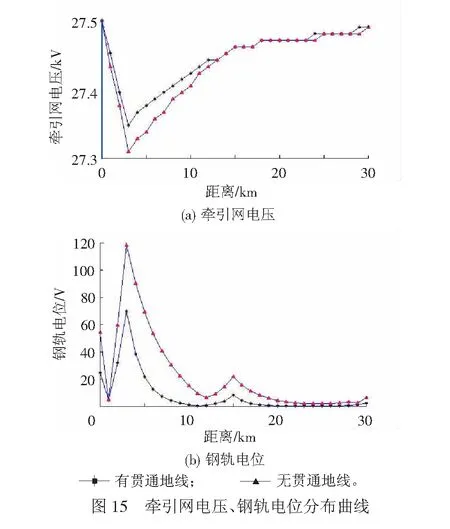
某一供电臂内有2个AT段，每个AT段长度为15 km。线路每隔1 km取一个测试点，改变动车组位置可以得到它在各位置时每个测试点牵引网电压和钢轨电位的分布情况。设钢轨对地电导为0.2 S/km，动车组电流为650 A。当动车组位于上行线距变电所3 km处，牵引网电压、钢轨电位分布曲线见图15。

图15(a)中牵引网电压在变电所处最高，为27.51 kV，然后呈逐渐下降的趋势，在动车组所在的位置(距变电所3 km)最低，为27.31 kV，随后网压逐渐升高，与文献[6]中理论计算结果较为接近，曲线趋势符合实际情况，可证明动车组在线路中运行时牵引网模型呈现出的电气特性符合现场反映的工况。加设贯通地线对牵引网电压有改善作用，牵引网最低电压变为27.35 kV。

图15(b)中动车组所在的位置钢轨电压最高，不加设贯通地线时钢轨电压高达118.1 V，加设贯通地线后钢轨电压降低为69.65 V，与文献[2, 21]中实测钢轨电位大小相符。可以看出设有贯通地线以后钢轨电位明显降低，说明贯通地线加入能够有效抑制钢轨电位。在3 km处动车组向钢轨注入电流，电流经钢轨、大地及贯通地线流向左右两个方向，一部分由自耦变压器流向它本身，另一部分从牵引变压器的中间抽头流回变电所，使得钢轨电位在牵引变电所、动车组处及自耦变压器处有3个极大值点。

加设贯通地线后当动车组分别处于上行线距变电所3、6、9、12 、15 km处牵引网电压、钢轨电位分布曲线见图16。

图16(a)中，动车组距牵引变电所3、6、9、12 km时牵引网电压的最小值呈现下降趋势，分别为27.35、27.27、27.22、27.21 kV。由于AT存在，动车组处于15 km处(靠近AT时)的牵引网电压为27.26 kV，较其处于AT段内时要大。

图16(b)中动车组分别处在距牵引变电所3、6、9、12 km的位置时，钢轨电压的最大值在70 V左右几乎保持不变。由于AT的吸上电流作用，动车组在15 km时钢轨电位最大值为29.17 V，然后向左右两侧逐渐递减，只存在2个极大值点。

4.3 高速铁路隧道及高架桥路段钢轨电位分布

高速铁路隧道与普通路段牵引网导线的参数有很大不同，隧道中的导线经受隧道中磁场和四周大地中磁场的共同作用；高架桥与普通路段也存在不同，供电回路与桥墩存在电气耦合现象，在桥墩回路产生的感应电压幅值为jωMI。当动车组位于上行线路距变电所3 km处，隧道、高架桥与普通路段钢轨电位分布见图17。

图17中动车组所在位置隧道钢轨电位为66.51 V，高架桥钢轨电位为88.25 V，普通路段钢轨电位为69.65 V。全线高架桥钢轨电位高于隧道、普通路段钢轨电位，究其原因为多导体传输线上电流在桥墩回路产生感应电压；桥墩对地阻抗存在压降，这些因素共同作用导致钢轨电压的抬升。此外，隧道中的导线经受隧道和四周大地中磁场的作用，对钢轨电位影响并不明显。为了进一步说明桥墩回路产生感应电压及桥墩对地阻抗存在的压降对钢轨电位的抬升程度。动车组位于上行线路距变电所3 km处，统计高架桥路段钢轨电位u1、普通路段钢轨电位u2、钢轨电位差Δu，见表7。

表7 高速铁路高架桥路段较普通路段钢轨电位抬升量

由表7可知，高速铁路高架桥路段相比于普通路段电压抬升量在5.32～33.41 V之间。考虑出现最大抬升电位处的高架桥路段钢轨电位仅为55.11 V，高架桥桥墩回路产生的感应电压及桥墩对地阻抗存在的压降对钢轨电位抬升作用明显，影响不可忽略。

在某AT段内线路为“普通+隧道”或“普通+高架桥”情况下，钢轨电位分布仿真结果见图18。其中在第一个AT段内普通线路长度为10 km，隧道与高架桥分别长5 km；第二个AT段普通线路长为15 km。从图18中可以看出，混合路段在9、10 km处钢轨电位出现先减后增的变化，主要原因为牵引网电气参数随路况的变化而变化，T、F、R、PW和G线上的电流将重新分配；高速铁路牵引网在10～30 km间混合路段的钢轨电位介于2种路段之间。

5 结论

本文在推导高速铁路全并联 AT 牵引网普通、隧道以及高架桥路段的数学模型的基础上，建立各路段牵引网子网模型，经级联形成牵引网链式网络模型。通过仿真和理论分析得到如下结论：

(1) 利用该模型进行的典型牵引网的仿真结果，对不同路段牵引网TR、TF型短路故障仿真的短路阻抗曲线趋势与实际相符，能够说明本文所搭建牵引网模型的正确性。

(2) 高速铁路牵引网加设贯通地线能够改善牵引网电压水平，有效抑制钢轨电位；负荷位置变动，网压最小值及钢轨电位最大值都将随其变动。

(3) 高速铁路高架桥路段桥墩回路产生感应电压以及桥墩对地阻抗存在的压降会显著的抬升钢轨电位，影响不可忽略。

(4) 隧道中的导线经受隧道磁场的作用，对线路钢轨电位影响并不明显；当线路出现“普通+隧道”、“普通+高架桥”路段时，牵引网各导线电流将重新分配。

参考文献：

[1] Mariscotti A, Pozzobon P. Determination of the Electrical Parameters of Railway Traction Lines:Calculation, Measurement and Reference Data[J]. IEEE Transactions on Power Delivery, 2004, 19(4): 1538-1546.

[2] Cella R, Giangaspero G, Mariscotti A. Measurement of AT Electric Railway System Currents and Validation of a Multi-conductor Transmission Line Model[J]. IEEETransactions on Power Delivery,2006,21(3):1721-1726.

[3] 吴命利. 电气化铁道牵引网的统一链式电路模型[J]．中国电机工程学报, 2010, 30(28): 52-58．

WU Ming-li．Uniform Chain Model for Traction Network of Electric Railways[J]．Proceedings of the CSEE, 2010, 30(28): 52-58．

[4] PILO E, ROUCO L, Fernandez A, et al. A Monuvoltage Equivalent Model of Bi-voltage Autotansformer-based Electrical System in Railway[J]. IEEE Transactions on Power Delivery, 2012, 27(2): 699-708.

[5] 吴命利, 范瑜, 辛成山. 电气化隧道中的导线-地回路阻抗[J]．中国电机工程学报, 2006，26(5)：176-181．

WU Ming-li, FAN Yu, XIN Cheng-shan. Impedance of Conductor-earth Circuits in Electric Railway Tunnel[J]．Proceedings of the CSEE, 2006, 26(5): 176-181.

[6] 何正友，方雷，郭东，等. 基于AT 等值电路的牵引网潮流计算方法[J]．西南交通大学学报, 2008，43(1): 1-7.

HE Zheng-you，FANG Lei，GUO Dong，et al．Algorithm for Power Flow of Electric Traction Network Based on Equivalent Circuit of At-fed System[J]. Journal of Southwest Jiaotong University, 2008, 43(1): 1-7.

[7] 胡海涛，何正友，汪江峰，等．基于车网耦合的高速铁路牵引网潮流计算[J]. 中国电机工程学报, 2012, 32(19): 101-108.

HU Hai-tao, HE Zheng-you, WANG Jiang-feng, et al. Power Flow Calculation of High-speed Railway Traction Network Based on Train-network Coupling System[J]. Proceedings of the CSEE, 2012, 32(19): 101-108.

[8] LEE Hanmin, LEE Changmu, JANG G, et al. Harmonic Analysis of the Korean High-speed Railway Using the Eight-port Representation Model[J]. IEEE Transactions on Power Delivery, 2006, 21(2): 979-986.

[9] 张杨，刘志刚．基于电磁暂态分析的高速铁路牵引网谐波模型及谐波特性分析[J]．电网技术，2011，35(5): 70-75.

ZHANG Yang, LIU Zhi-gang．Modeling and Characteristic Analysis of Harmonic in High-speed Railway Traction Network Based on PSCAD/EMTDC Platform[J]. Power System Technology，2011，35(5): 70-75.

[10] 胡海涛，何正友，张民，等．高速铁路全并联AT供电系统串联谐振分析[J]. 中国电机工程学报, 2012, 32(13): 52-60.

HU Hai-tao，HE Zheng-you，ZHANG Min，et al．Series Resonance Analysis in High-speed Railway All-parallel AT Traction Power Supply System[J]. Proceedings of the CSEE, 2012, 32(13): 52-60.

[11] 王斌，高仕斌，黄文，等．高速列车再生制动工况时牵引供电系统谐波传输特性分析[J]. 电网技术, 2014, 38(2): 489-494.

WANG Bin，GAO Shi-bin，HUANG Wen，et al．Analysis on Harmonic Transmission Characteristics of traction Power Supply System during Regenerative Braking of High Speed Train[J]. Power System Technology, 2014, 38(2): 489-494.

[12] TYLAVSHY D J, BROWN K A, MA T T. Closed-form Solution for Underground Impedance Calculation[J]. Proceedings of the IEEE, 1986, 74(9): 1290-1292.

[13] 柯尊平. 牵引网电抗参数的简易计算[J]. 铁道学报, 1997, 19(2): 43-48.

KE Zun-pin. A Solution Method for Unit Reactance of Traction Power Contact Line[J]. Journal of the China Railway Society, 1997, 19(2): 43-48.

[14] TYLAVSHY D J. Conductor Impedance Approximations for Deep-underground Mines[J]. IEEE Transactions Industry Applications, 1987, 23(4): 723-730.

[15] 高国强. 高速列车运行状态暂态过电压机理与抑制方法的研究[D]. 成都: 西南交通大学, 2012.

[16] 马庆安, 朱小军, 郭楷, 等. 三种AT供电模式的比较[J]. 铁道学报, 2012, 34(3): 34-39.

MA Qing-an, ZHU Xiao-jun, GUO Kai, et al. Comparison of Three Modes of AT-feeding System[J]. Journal of the China Railway Society, 2012, 34(3): 34-39.

[17] 邓云川. 综合接地系统钢轨电位及电流分布的分析[J]. 铁道标准设计, 2009,(S1): 153-156.

DENG Yun-chuan. Analysis of Rail Potential and Current Distribution of Integrated Grounding System[J]．Railway Standard Design, 2009,(S1): 153-156．

[18] PAUL C R. Analysis of Multi Conductor Transmission Lines[M]. New York: Wiley, 1994: 15-40.

[19] 冯金博. 高速铁路车网匹配研究[D]. 成都: 西南交通大学, 2011.

[20] 林国松. 牵引供电系统新型保护与测距原理研究[D]. 成都: 西南交通大学, 2010.

[21] 雷栋, 董安平, 张雪原, 等. 重载电气化铁道钢轨电位的测试与分析[J]. 铁道学报, 2010, 32(5): 41-46.

LEI Dong，DONG An-ping，ZHANG Xue-yuan，et al．Test and Analysis of Rail Potentials of Heavy Haul Electric Railways[J]．Journal of the China Railway Society, 2010, 32(5): 41-46．