高速铁路区间能力全失效条件下列车运行实时调整研究

占曙光， 赵 军， 彭其渊， 徐培娟， 张馨竹

(西南交通大学 交通运输与物流学院，四川 成都 610031)

高速铁路列车运行安全和非正常情况下列车运行实时调整(下文简称“调整”)是铁路调度指挥关注的重点问题。由于高速铁路速度高、密度大，任何干扰因素都有可能扰乱列车正常运行，导致运行秩序紊乱，甚至出现运行事故。对高速铁路列车运行产生干扰的因素有很多，主要包括不良天气、人为失误以及线路、通信信号、动车组故障等。高速铁路对这些干扰具有很强的脆弱性，极易造成列车偏离原定的运行计划。因此，对干扰条件下的调整进行研究具有非常重要的现实意义。

根据对列车运行的影响程度，高速铁路干扰因素主要可分为影响程度相对较小的干扰和影响程度相对较大的干扰。目前，在学术界，2种类型的干扰没有明确的界定，大部分学者认为：小干扰往往来源于列车在站时的到发晚点，此时不需要对列车运行进行较大调整，也不需对动车组、乘务组等资源的任务重新进行调整，仅需利用运行图的冗余时间对列车到发时刻进行微调便可使列车恢复正常运行；大干扰往往来源于铁路基础设施由于故障在相对较长的时间内不能正常使用，从而导致列车大面积晚点，此时为恢复列车正常运行，不仅需要大规模调整运行图，也需要同时调整动车组和乘务组等资源的任务。

本文研究高速铁路区间能力全失效时的调整问题，区间能力全失效指由于故障干扰导致某区间上下行2条正线同时中断，该问题属于大干扰条件下的调整问题。当区间能力全失效时，调度员需分别对运行图、动车组和乘务组进行调整。3项调整任务彼此相互影响，理想化的解决方案为将3项调整任务集成优化，但将使整个问题变得非常复杂。比较可行的解决方案是将整个问题分解为运行图调整、动车组调整和乘务组调整3个子问题，进而依次求解，尽管该方案只能获得近似解，但更适用于实时调整环境。本研究侧重于运行图实时调整，当干扰导致区间能力全失效时，调度员优先安排接近中断区间的列车在适当车站停车等待干扰结束。若干扰造成的列车晚点情况非常严重，调度员可选择取消部分列车运行。当干扰结束后，调度员需慎重安排停站列车的出发顺序和时刻，以最大程度地减小干扰对列车运行的影响。

当前，国外学者对调整问题开展较系统地研究，较为全面的综述见文献[1]；文献[2-6]研究小干扰条件下的调整，将该问题视为无等待的作业车间调度问题，提出基于比选图的优化模型和算法；文献[7-10]探讨另一类小干扰条件下的调整，称为晚点管理问题，判断在接续车站前行列车是否等待后续晚点列车，对不同约束下的问题建模，设计有效的求解算法。最近，文献[11-12]研究大干扰条件下的调整，文献[11]对区间在全部封锁和部分封锁情况下的干扰时段的调整，分别构建整数规划模型，模型由商业优化软件CPLEX直接求解；在文献[11]的基础上，文献[12]提出更一般化的区间能力失效情况下的调整模型。国内对此研究相对较少，文献[13-14]研究单线铁路在区间能力失效条件下的调整，针对线路失效持续时间的不确定性，文献[13]构建两阶段带补偿随机期望模型，基于多阶段递归决策概念模型，提出不完全连续多阶段决策模型，并开发分支定界算法对所提出的模型进行求解；文献[14]提出基于场景的滚动时域算法，进一步采用多层分支求解策略对问题求解；基于文献[13-14]的研究，考虑干扰持续时间的不确定性,文献[15-16]分别对双线铁路和双线铁路网络在干扰条件下的调整进行研究，提出基于模糊数学的优化模型和求解算法。

综上，只有文献[11-12]探讨大干扰条件下的调整问题，研究对象为荷兰铁路，采用1 h或0.5 h周期运行图，且列车速度等级较为单一。然而，我国已经投入运营的高速铁路(例如京沪、京广高铁)采用非周期运行图(或可视为以24 h为周期的运行图)，并存在2种速度等级列车共线运行。相比国外，我国高速铁路运行图规模更大、运营模式更为复杂，但至今鲜见文献探讨符合国情的严重干扰时列车运行实时调整问题。鉴于此，作者在文献[11-12]基础上，根据我国实际情况，研究区间能力全失效条件下的调整问题。首先，借助于事件-活动网络概念，构建大规模混合整数线性规划模型;其次，根据问题特点，开发有效的两阶段求解算法;最后，结合中国高速铁路实际，构造算例验证所提方法的效果和效率。

1 问题描述与界定

1.1 问题描述

以由4个车站、3个区间、4列列车运行的高速铁路为例，对问题的描述见图1。已知上行方向有4列高速列车运行。其中G1、G3时速为300 km，D2、D4时速为250 km。(图1仅为示意图，省略部分列车在中间站的停车过程)在时刻t1，因某种故障干扰，导致区间3的2条正线完全中断，4列列车不能按图定要求继续运行。为保证干扰情况下列车运行的安全，4列列车均应在进入中断区间之前停车。由于车站能力限制，每个车站容纳的停车待避列车数量不能超过其能力。假设车站2和车站3分别只有2条可使用的股道，调度员需决策如何安排G1、D2、G3、D4列车在车站2和车站3的停站方案，既保证安全又使列车晚点最少。假设在时刻t2干扰结束，调度员还需决策4列列车的出发顺序和时刻，将干扰的影响降至最小。此外，由于列车G3和D4在干扰发生时还没有从始发站出发，调度员可根据现场情况并结合实时信息，综合判断是否需要采取停运措施。研究重点在于通过构建优化模型，在保证各类列车运行约束的前提下，对上文提出的问题进行优化，提供实时的列车运行调整策略，以协助调度员的调度决策。

1.2 问题界定

区间能力全失效情况下调整是非常复杂的决策问题，调度员进行调整工作时需考虑许多因素，包括干扰影响范围、持续时间、干扰类型、当前列车运行状态、干扰处理方式以及动车组周转情况等。为研究方便，作以下假设:

假设1 各车站到发线分上下行分别使用，各到发线与同方向正线相连，且配有供旅客乘降的站台；

假设2 动车组数量足够，不考虑动车组数量限制和运用优化的问题；

假设3 进入中断区间的列车已经通过故障地点，可继续向前运行；

假设4 干扰发生前列车按运行图正常行驶，干扰发生后受影响的列车停留在有剩余能力的车站，不安排在区间停留。

2 模型构建

2.1 问题抽象

为建模方便，从宏观层面上把高速铁路列车运行描述为由事件和活动构成的网络。事件表示列车发出或到达车站；活动连接2个相邻事件，可进一步分为列车活动和间隔活动。

(1) 列车活动

既可视为区间运行活动，表示列车在相同区间2个关联车站的出发事件与到达事件之间的活动；也可视为车站停站活动，表示列车在相同车站到达事件与出发事件之间的活动。

(2) 间隔活动

既可视为2列车在相同区间的运行间隔活动，包括在某区间一端车站的出发间隔活动和在另一端车站的到达间隔活动；也可视为2列车在相同车站的发到间隔活动。

目前，我国高速铁路普遍采用2种速度等级列车共线运行模式，即同线路上运行着时速300 km的高速列车(定义为Ⅰ类列车)和时速200 km ～ 250 km的中速列车(定义为Ⅱ类列车)。下面结合该运输组织模式进行研究。

2.2 目标函数及基本模型

由既有文献可看出，高速铁路区间能力全失效条件下的调整为复杂的组合优化问题。为最大程度地减小干扰对列车运行的影响，以总加权求和列车取消惩罚值和列车晚点惩罚值最小为目标函数。不考虑运营安全和设备能力约束的基本模型为

( 1 )

s. t.M1yte≤xe-qe≤M1∀e∈E1

( 2 )

M1yte≤xe-qe≤M1∀e∈E2

( 3 )

yt∈{0,1} ∀t∈T

( 4 )

xe∈N∀e∈E

( 5 )

( 6 )

式中：T1、T2分别为Ⅰ、Ⅱ类列车集合；T为所有列车集合；t为列车索引；λt为列车t取消的惩罚系数；E1、E2分别为Ⅰ、Ⅱ类列车相关事件集合；E为所有事件集合；e为事件索引；μe为事件e单位晚点惩罚系数；yt为0-1变量，定义见式( 6 )；xe、qe分别为事件e在调整后的运行图以及原始运行图中的发生时刻；te为事件e对应的列车；M1为充分大正数，取M1=1 440；N为自然数。约束(2)和约束(3)表示列车在车站实际的到发时刻不能早于图定的到发时刻。此外，该组约束将取消的列车移动到研究的时间范围之后，即被取消列车对应事件e的实际发生时刻xe=qe+M1，若取M1=1 440。因为高速铁路的运营时间最大不超过M1，意味着将被取消的列车移动到运营时间结束之后。通过把取消列车移动到最后，可有效避免该类列车相互间及与其他未被取消列车之间的影响；约束(4)和约束(5)表示变量的取值范围。

2.3 约束条件

为确保高速铁路行车安全，列车在高速铁路上运行还需满足多种运营安全和设备能力约束，包括单列列车运行约束、相邻列车间隔约束、车站能力约束、取消列车约束、列车区间最长运行时间约束及列车发车时刻约束等。

(1) 单列列车运行约束

正常情况下，列车按照原定运行图运行。发生干扰后，虽受到干扰的影响，但各列车从始发站到终到站经过的所有事件e和活动a的顺序固定不变，需满足区间的运行时间约束和在站停站时间约束，即

xf-xe≥La∀a=(e,f)∈Atrain

( 7 )

式中：e、f分别为某列车先后占用相同资源(区间或车站资源)的2个相邻事件；Atrain为列车活动集合；a为活动索引，a=(e,f)∈Atrain既可为列车在区间的运行活动，也可为列车在车站的停站活动;La为活动a的最短持续时间,当a为区间运行活动时，La为列车在区间的最小运行时间；当a为车站停站活动时，La为列车在车站的最小停站时间。

(2) 相邻列车间隔约束

为避免列车发生冲突，相邻列车在区间运行或在站发到均需满足间隔约束。本节仅建立区间运行间隔约束模型，在站到发间隔约束放在车站能力约束部分。另外，发生干扰时，不论同等级或不同等级列车均可能在车站发生越行。因此，2列车在站的到发顺序可能产生变化，定义表示事件发生先后顺序的0-1变量λef，即

( 8 )

列车区间运行间隔约束为

xf-xe+M2(1-λef)≥La

( 9 )

(10)

我国高速铁路为双线单向铁路，同方向运行的列车只能在车站而不能在区间越行。为避免同方向的2列车在区间越行，约束条件为

te=te′tf=tf′(si,si+1)∈Seg

(11)

(3) 车站能力约束

列车到达或者通过车站必须占用车站线路，相同线路在同一时间仅允许1列车占用，而各站线路数量有限，所以列车运行必须满足车站线路能力的限制。鉴于始发站s1和终到站sn为较大车站，能力充足，在此仅考虑中间站能力约束。定义Sm为中间站集合，si∈Sm，si≠s1，si≠sn。为满足车站能力约束，每个中间站需为每列车分配1条站线，即当列车到达时至少应有1条空闲线路供其使用。因此，当某列车到达某车站时，可先统计已经到达和发出的列车总数，两者之差获取此时停留在该站的列车数，进而用车站线路数减去停留的列车数便可获得空闲的线路数。

φa=

(12)

(13)

xf-xe+M2(1-φa)≥La

(14)

(4) 干扰发生后列车取消约束

当干扰导致某区间能力全失效时，该区间完全中断，通行能力为0，导致整条线路列车运行受到严重影响。如前所述，若干扰造成列车大面积晚点，调度员针对不同列车将采用不同的停运调整策略。对发生干扰时已经在线路上载客运行的列车，由于取消该部分列车存在诸多困难，例如清客、退票、赔偿等，通常采取的措施为合理调度列车在适当的车站停车等待干扰恢复。然而，对于干扰发生时还未从始发站出发的列车，调度员可根据现场情况、干扰信息、以及客票发售情况等，综合决策是否停运，以尽量减小干扰对整条线路造成的影响。鉴于此，取消列车约束为

(15)

(16)

式中：tdep为列车t在始发站的出发时刻。

式(15)和式(16)表示只有始发时刻晚于干扰发生时刻的列车才能考虑取消运行。

(5) 干扰发生后列车区间最长运行时间约束

由假设4，干扰发生后还未进入中断区间的列车需依次停在合适的车站，而目前创建的约束可能导致调整方案中部分列车在区间过度缓行甚至停车。为避免这种情况，提出列车区间最长运行时间约束，即

∀a=(e,f)∈ArunArun⊂Atrain

(17)

(6) 干扰发生后列车发车时刻约束

(18)

(7) 有效不等式约束

显然，若某列车从某站出发，另一列车尚未到达该站，同样该列车到达该站时也必定在另一列车到达该站之前。虽然此约束已隐含在前文的约束中，但是加上该约束后更有利于加快模型的求解速度。有效不等式为

(19)

式中：e′为列车te在车站s的出发事件；a′为活动索引。式(19)表示若列车te在列车tf到达s站之前从s站出发，则列车te也一定在列车tf之前到达s站。

2.4 模型合理性说明

约定干扰发生后，未进入中断区间的列车只能依次停留在适当的车站。由于我国高速铁路在相同线路上同时开行2种速度等级的列车，Ⅰ类列车的优先级高于Ⅱ类列车，当干扰发生后，应如何制定列车停站方案，以便既能充分体现不同等级列车的优先级，又能有效避免获得不合理的列车运行调整方案。本节通过对Ⅰ、Ⅱ类列车赋予不同的取消惩罚系数λt和晚点惩罚系数μe，再基于车站能力约束3、干扰发生后列车区间最长运行时间约束5、以及干扰发生后列车发车时刻约束6建立模型，可完全自动确定干扰发生后基于优先级的列车停站方案，且避免产生不合理的列车运行调整方案，案例见图2。

图2中，已知车站s3和s4上行方向各有2条股道可使用，干扰发生在s4与s5之间的区间，此时有4列Ⅰ类列车和1列Ⅱ类列车正在运行，车次分别为G1、G3、G4、G5和D2。干扰发生时，对于列车D2和G3，尽管列车D2早于列车G3进入区间(s2,s3)，但由于Ⅰ类列车优先级高于Ⅱ类列车，列车D2可能将提前在s3站停车等待，让G3先行。当然，对于列车D2和G3，谁在s3站等待，谁继续向前运行，模型根据列车惩罚系数自动确定。对于列车G1、G3和G4，由于车站s4只有2条股道可使用，受车站能力约束限制，列车G4只能等待列车G1或者G3从车站s4出发之后才能进入该站。从理论上看，列车G4可提前在时刻t1从车站s3出发，然后通过区间(s3,s4)缓慢运行进入车站s4。但是，鉴于干扰持续时间的不确定性，此种调整策略不具有运营可行性。由于列车G4在区间(s3,s4)需满足最长运行时间约束，因而只能在车站s3停车等待，直到时刻t2才能出发。同理，列车G5也只能在车站s2等待，直到车站s3有列车出发释放线路能力之后，才能在时刻t3从车站s2出发。

当调度员在实际工作中面临区间能力全失效时，通常的做法为：干扰发生时，已始发的列车根据当时所处的位置依次就近在有能力的车站停车等待，未始发的列车推迟出发；干扰结束时，各站的列车按照图定顺序依次发出。为便于比较，将现场调度员采用的策略称为基于顺序的调整方案，而将本文提出的调整策略称为基于优先级的调整策略。

3 算法设计

2.2和2.3小节建立的模型属于混合整数线性规划模型(MILP)的范畴，计算复杂度属于NP-hard问题，针对大规模问题很难求得最优解。实际工作中，高速铁路的列车运行调整过程分阶段进行，此外，由于干扰持续时间的不确定性，调度员需根据现场反馈的最新信息动态地对列车运行进行调整。因此，提出两阶段算法，对整个问题进行分解，可快速求解大规模实际问题，实时给出列车运行调整方案。

车站能力约束是调整问题求解的难点所在，而且该问题在干扰结束前后的时间段内表现尤为突出。因此，将原问题分解为2个阶段：第1阶段忽略干扰结束后时段车站能力约束，对原问题优化，虽然获得的解从整体上看可能不可行(干扰结束之后时段的调整方案不一定可行)，但是可获得整个干扰结束之前时段可行的调整方案；第2阶段固定第1阶段获得的干扰结束之前时段的调整方案，并完整考虑干扰结束之后时段的车站能力约束，对原问题重新进行优化，进而得到整个问题可行的调整方案，具体求解步骤为

Step1仅对干扰结束时刻之前时段施加车站能力约束，在干扰结束之后时段，假设车站能力不受限制(即去掉车站能力约束(13)、约束(14))，对原问题求解，获得调整后的运行图φ1。在干扰结束之前时段，列车按照φ1运行；

Step2在第1阶段获得的调整图φ1基础上，考虑干扰结束之后时段的车站能力约束(即加上车站能力约束(13)、约束(14))，固定第1阶段获得的调整图φ1中干扰结束之前的部分，重新对原问题进行求解，获得全时段可行的调整图φ2，最终获得全天可行的调整图。

分析两阶段算法的性质可看出:第1阶段省略干扰结束之后时段车站能力约束，可有效降低问题的规模和求解难度；第2阶段固定第1阶段获得的结果，即干扰结束之前部分，相比于原问题，该阶段的求解难度也得到明显缓解。由于车站能力紧张主要集中在干扰结束前后较小的时段，两阶段法对调整结果的影响主要也集中在该时段。具体而言，因为在第2阶段固定第1阶段在该时段的调整结果，有可能导致整体调整结果质量下降。由于影响时段不会太长，可预计两阶段法能在一定程度上保证整个问题的求解质量。

与整体优化相比，两阶段算法属于启发式算法范畴，并不能保证获得问题的全局最优解。但当高速铁路受到严重干扰时，快速提供近似最优调整图比漫长等待最优调整图更重要。因此，对于大规模调整问题，两阶段算法具有较好的可行性和实用性。

4 算例分析

4.1 算例描述及参数设置

以京沪高速铁路为例，利用2013年调整后的列车运行图相关数据进行算例分析。京沪高速铁路由北京南站至上海虹桥站，途经23个车站(不包括天津西站)，全线分为22个区间。当区间能力全失效时，上下行的列车运行调整问题大致相同。因此，仅对上行列车进行算例分析，选择从上海虹桥站至北京南站的42列列车(包括从杭州等地经过上海虹桥到达北京南站的跨线列车)。其中，时速300 km的Ⅰ类列车共40列，时速250 km的Ⅱ类列车共2列，对模型进行验证。

本文基于已知干扰持续时间，通过调整干扰发生时刻和地点，设计3种测试场景，每种场景通过变化干扰持续时间分别设置3种干扰情景，算例具体设置为

场景1

09:00苏州北站-无锡东站之间出现列车运行干扰，导致区间通行能力全部丧失，通过调整干扰持续时间，设置3种干扰情景，干扰持续时间分别为30 min、45 min及60 min；

场景2

12：00宿州东站-徐州东站之间出现列车运行干扰，导致区间通行能力全部丧失30 min、45 min及60 min；

场景3

16：00济南西站-德州东站之间出现列车运行干扰，导致区间通行能力全部丧失30 min、45 min及60 min。

为便于表示不同场景下的干扰情景，定义三元组(a,b,c)。其中，a为干扰发生时刻，b为干扰所在区间，c为干扰持续时间。3种测试场景下9种干扰情景见表1。

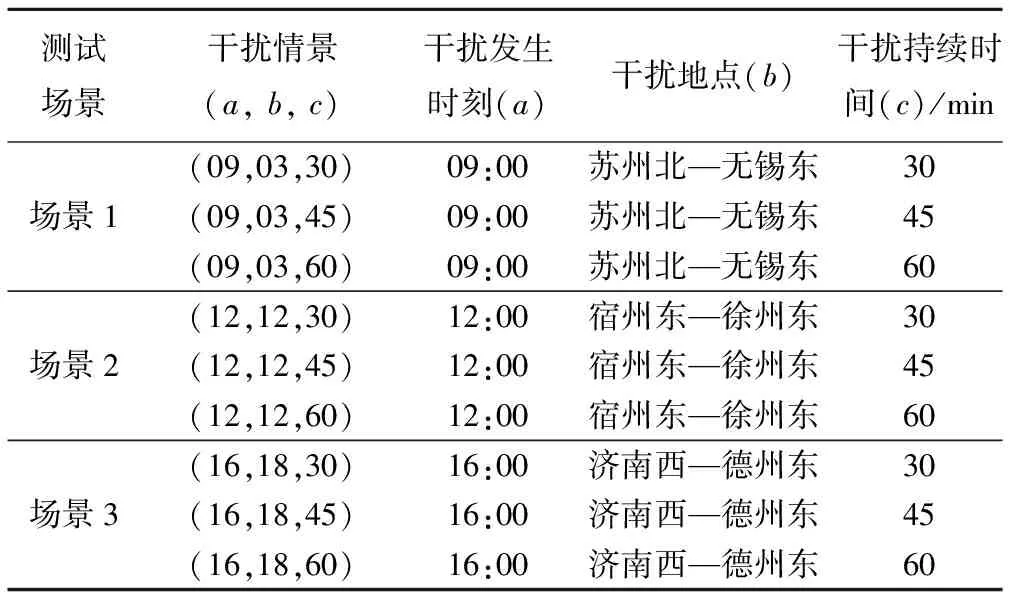
表1 干扰情景的三元组表示

算例中，列车区间运行时间和停站时间由原始列车运行图给出，列车区间运行时间取“京沪高铁区间运行时间标准”相应数值。其中，区间最小运行时间取区间纯运行时间，区间最大运行时间取区间纯运行时间加上Ⅰ类列车起停附加时间5 min，列车在站最小停站时间取为原始运行图上的停站时间。中间站可使用的到发线数量参照“京沪高速铁路动车组停车站到发线安排”取值，见表2。由于算例仅考虑42列长途列车，该部分列车的数量仅占实际全部开行列车的一半。因此，中间站能力仅取实际能力的0.5。减小车站能力时，充分保证原始运行图的可行性，即如果根据原始运行图在某站存在列车越行，那么该站必须保证最少有2条线路可使用。表2中，股道数所在列括号内的第1个数值表示上行方向列车实际可使用的股道数量，第2个值表示上行方向列车在算例中可使用的股道数量。根据参考文献[17]以及京沪高速铁路的实际资料，相邻列车之间的最小发车间隔取2 min、最小到达间隔取3 min，列车在相同到发线的发到间隔取3 min。目标函数中，Ⅰ、Ⅱ类列车取消运行的惩罚值按票价比分别取1 000和600，同时，2类列车到站晚点1 min的惩罚值也根据票价比分别取5和3。考虑取消列车对旅客产生的影响很大，列车取消惩罚值相对比较大，具体取值根据现场经验灵活调整，在此不作重点研究，如果有需要，可对多组取值进行计算。M1取1 440，M2取2 880。2类列车区间运行时间见表3。

表2 中间站股道数量

注：昆山南站为京沪高铁和沪宁城际共用；南京南、济南西站虽为大站，但由于没有列车在此越行，假设只有1条股道可供长途列车使用。

表3 区间运行时间(不包括起、停附加时分)

注：起停附加时分 Ⅰ类列车起2 min、停3 min；Ⅱ类列车起停均为2 min。

4.2 算例结果

使用CPU为Inter(R)Core(TM)i5-4570 3.2 GHZ、内存为4 GB的电脑，采用IBM ILOG OPL (Optimization Programming Language)编程，调用CPLEX 12.6实现提出的方法。CPLEX的相关参数设置为默认值，通过内置的将分支定界法和割平面法相结合的分支切割算法对混合整数线性规划模型进行求解。鉴于列车运行调整的实时性要求，限制最长运行时间为120 s，依据4.1节设置的算例及相关参数，对3种测试场景下的9种干扰情景分别进行计算，得到基于优先级调整策略的计算结果见表4。

表4 基于优先级调整策略的计算结果

借助提出的整体优化模型，在设定的限制时间内，干扰情景(12,12,60)不能求得整数解。因此，使用第3节描述的两阶段算法对该干扰情景下列车运行调整方案进行分阶段求解。表4中，第7行为干扰情景(12,12,60)利用整体优化模型求解的结果(在120 s内无解)，第8行为该情景在两阶段算法下第1阶段求解的结果，第9行为该情景在两阶段算法下第2阶段求解的结果。为评估两阶段算法的效果，在不限计算时间的前提下，采用整体优化模型对干扰情景(12,12,60)重新进行求解，结果经过3 383 s求得最优解为9 120。从2种方法的求解结果可看出，与整体优化模型相比，两阶段算法在目标函数值上的误差为2.68%，可见两阶段算法具有较高的求解质量。

从表4可看出，不同的干扰情景对列车运行的影响各不相同。中午时刻发生在线路中部的干扰对列车运行影响最为严重，如场景2大于场景1和3。同一场景下，干扰持续时间越长，对列车运行的影响越大。基于优先级的调整策略能够快速有效地获得不同干扰情景下的列车运行实时调整方案，且绝大多数调整方案可在100 s以内获得。针对较复杂的干扰情景，如干扰情景(12,12,60)，采用两阶段算法后只需不到150 s便可获得可行的列车运行调整方案，且获得的解与最优解的误差仅为2.68%。由此可见，本文提出的方法计算效果和效率可满足实时列车运行调整的需要。

4.3 调整策略的比较

如前所述，现场区间能力全失效时，高铁调度员通常采用基于顺序的调整策略开展列车运行调整工作。该策略下，4.1节算例计算结果见表5。

表5 基于顺序调整策略的计算结果

注：计算时间指该干扰情境下列车运行调整方案的计算机求解时间。

比较表4和表5可发现，在相同干扰情景下，采用优先级调整策略获得的结果明显优于顺序调整策略。与顺序调整策略相比，基于优先级调整策略使目标函数值(总加权求和列车取消惩罚值和列车晚点惩罚值)减小近50%,同时，取消的列车数量也大为减小(事实上，对于9种干扰情景，只在2种干扰情景下各取消1列列车)，见图3和图4。由此可见，优先级调整策略可在保证列车安全运行的前提下，较大地减小干扰对列车运行的影响。

4.4 车站能力的影响分析

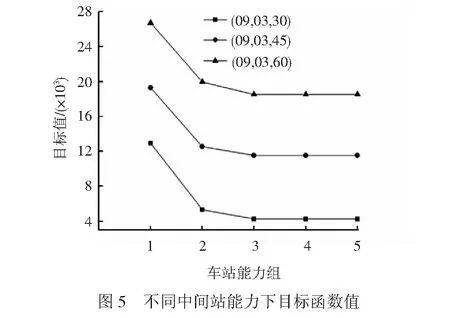
车站能力是列车运行实时调整问题的重要约束，4.1节构造测试算例时，为更好地测试所提方法的效果，将各站的能力设置为实际能力的0.5倍。为评估车站能力对高速铁路抗干扰的影响，在保证原始运行图可行的前提下，构造5组中间站能力值，详见表6。对于测试场景(09，03，-)的3种干扰情景，在不同的中间站能力组合下，基于优先级调整策略的计算结果见图5。从图5可知，在一定的范围内，随着中间站能力的增加，高速铁路抗干扰能力也随之增加，当中间站能力增加到一定程度时，高速铁路抗干扰能力保持不变，意味着对于抗干扰能力较差的高速铁路，若条件允许，可考虑在干扰多发地段附近的中间站上增设1～2条到发线，以提高列车运行调整的质量。

表6 中间站能力值

5 结论

(1) 通过引入事件和活动的概念，将高速铁路从宏观层面抽象为由事件和活动构成的网络，在此基础上，对高速铁路区间能力全失效条件下调整问题进行阐述；

(2) 考虑运营安全和设备能力等约束，对高速铁路区间能力全失效条件下的调整问题，建立基于优先级调整策略的MILP模型；

(3) 结合高速铁路调度指挥分阶段逐步进行的实际情况，提出两阶段求解算法，保证求解质量的同时，提高求解速度；

(4) 以京沪高速铁路上行方向全天42列长途列车实际数据为背景，构造产生于3种测试场景下的9种干扰情景，对提出的整体优化模型和两阶段求解算法进行测试。通过与现场实际采用的顺序调整策略相比，突出基于优先级的调整策略在保证行车安全的基础上，可减小干扰对列车运行的影响；

(5) 干扰条件下的调整是极其复杂的决策问题，涉及到铁路运输系统的各环节。目前本文主要针对宏观层面的运行图进行调整，没有考虑动车组和乘务组方面的约束，也没有从微观层面上对干扰的类型进行分析。另外，测试算例仅对京沪高铁单方向的部分列车进行分析，今后将进一步对整条线路上开行的所有列车以及从整个路网层面上进行优化。最后，随着问题的规模进一步扩大，如何选择更为有效的启发式算法提高运算效率，如滚动时域算法等将是研究的重点。

参考文献：

[1] CACCHIANI V, HUISMAN D, KIDD M P, et al. An Overview of Recovery Models and Algorithms for Real-time Railway Rescheduling[J]. Transportation Research Part B: Methodological, 2014, 63:15-37.

[2] D’ARIANO A, PRANZO M, HANSEN I A. Conflict Resolution and Train Speed Coordination for Solving Real-time Timetable Perturbations[J]. IEEE Transactions on Intelligent Transportation Systems, 2007, 8(2):208-222.

[3] CORMAN F, D’ ARIANO A, PACCIARELLI D, et al. Bi-objective Conflict Detection and Resolution in Railway Traffic Management[J]. Transportation Research Part C: Emerging Technologies, 2012, 20(1): 79-94.

[4] CORMAN F, D’ ARIANO A, PACCIARELLI D, et al. Centralized Versus Distributed Systems to Reschedule Trains in Two Dispatching Areas[J]. Public Transport, 2010, 2(3): 219-247.

[5] CORMAN F, D’ ARIANO A, PACCIARELLI D, et al. A Tabu Search Algorithm for Rerouting Trains During Rail Operations[J]. Transportation Research Part B: Methodological, 2010, 44(1): 175-192.

[6] CORMAN F, D’ ARIANO A, HANSEN I A, et al. Optimal Multi-class Rescheduling of Railway Traffic[J]. Journal of Rail Transport Planning & Management, 2011, 1(1): 14-24.

[7] GINKEL A, SCHOBEL A. To Wait or not to Wait? The Bicriteria Delay Management Problem in Public Transportation[J]. Transportation Science, 2007, 41(4): 527-538.

[8] SCHACHTEBECK M, SCHOBEL A. To Wait or not to Wait-and Who Goes First? Delay Management with Priority Decisions[J]. Transportation Science, 2010, 44(3): 307-321.

[9] DOLLEVOET T, HUISMAN D, SCHMIDT M., et al. Delay Management with Rerouting of Passengers[J]. Transportation Science, 2012, 46(1): 74-89.

[10] DOLLEVOET T, HUISMAN D, KROON L G, et al. Delay Management Including Capacities of Stations[J]. Transportation Science, 2014,49(2):185-203.

[11] LOUWERSE I, HUISMAN D. Adjusting a Railway Timetable in Case of Partial or Complete Blockades[J]. European Journal of Operational Research, 2013, 235(3):583-593.

[12] VEELENTURF L P, KIDD M P, CACCHIANI V, et al. A Macroscopic Railway Timetable Rescheduling Approach for Handling Large Scale Disruptions[C]//Technical report ERS-2014-010-LIS, Erasmus Research Institute in Management (RRIM), 2014. URL http://hdl.handle.net/1765/51678.

[13] 孟令云，杨肇夏，李海鹰. 单线铁路区间能力失效条件下列车运行调整模型[J]. 系统工程理论与实践，2012，32(4)：885-894.

MENG Ling-yun, YANG Zhao-xia, LI Hai-ying. Train Dispatching Models under Field Capacity Breakdowns on Single-track Railway Lines[J]. Systems Engineering Theory & Practice, 2012,32(4)：885-894．

[14] MENG L，ZHOU X. Robust Single-track Train Dispatching Model under a Dynamic and Stochastic Environment: A Scenario-based Rolling Horizon Solution Approach[J]. Transportation Research Part B: Methodological, 2011, 45(7): 1080-1102.

[15] YANG L, ZHOU X, GAO Z. Rescheduling Trains with Scenario-based Fuzzy Recovery Time Representation on Two-way Double-track Railways[J]. Soft Computing, 2013, 17(4):605-616.

[16] YANG L, ZHOU X, GAO Z. Credibility-based Rescheduling Model in a Double-track Railway Network: a Fuzzy Reliable Optimization Approach[J]. Omega, 2014, 48:75-93.

[17] 史峰，魏堂建，周文梁，等. 考虑动车组周转和到发线运用的高速铁路列车运行图优化方法[J]. 中国铁道科学，2012,33(2): 107-114.

SHI Feng, WEI Tang-jian, ZHOU Wen-liang, et al. Optimization Method for Train Diagram of High-speed Railway Consider the Turnover of Multiple Units and the Utilization of Arrival-departure Tracks[J]. China Railway Science, 2012, 33(2):107-114.