钢轨轮廓全断面高精度动态视觉测量方法研究

占 栋， 于 龙， 肖 建， 陈唐龙

(西南交通大学 电气工程学院， 四川 成都 610031)

为适应日益繁重的轨道运输需要，轨道交通管理部门加快了列车运行速度，提高了列车轴重和行车密度，增加列车长度并混合列车编组，钢轨的工作负荷明显增加，工作环境更加复杂，导致钢轨磨耗加快，局部线路钢轨波磨、剥离、压溃等病害现象突出，增加了钢轨维护难度[1-4]。

轨道检测车是检查轨道病害、指导轨道维修作业、评价轨道服役性态和保证轨道交通运输安全的重要基础装备。上世纪50年代起，我国一直致力于轨道检测车的研制，在引进、消化和吸收国外轨道检测技术的基础上，相继成功研发出适合于我国的多种型号轨道检测车，为我国轨道交通运营维护发挥了巨大作用[5-6]。钢轨轮廓动态测量作为轨道检测关键技术，在轨道检测中占有重要地位[7-10]，其检测结果可直接用于轨道几何参数计算，同时为钢轨表面故障甄别、钢轨服役性态评估、钢轨缺陷演变机理研究提供客观依据。

国内外学者、研究机构一直十分重视钢轨轮廓测量，先后在钢轨轮廓测量图像识别、视觉传感器标定和钢轨轮廓特征提取方面开展了系列研究。AlIPPI等[11]最先提出采用激光摄像技术进行钢轨轮廓动态测量，重点研究了神经网络方法在钢轨激光轮廓图像识别中的应用；POPOV等[12]研究了基于线性模型的激光摄像式传感器标定方法，并应用在莫斯科地铁轨道检测系统中；MAURO等[13]介绍了意大利轨道交通基础设施动态测量技术，包括钢轨轮廓动态测量技术；孙军华等[14]提出一种Kalman滤波和Hessian 矩阵相结合的钢轨激光光条中心快速提取方法；LIU等[15]考虑车体振动，提出了一种新型钢轨磨耗动态测量方法，并进行了实际应用；占栋[16]在钢轨轮廓测量视觉传感器传统标定方法的基础上，采用非线性模型对视觉测量方法进行了改进和优化，提高了传感器测量精度。

目前国内轨道检测车中普遍配备的是2组激光摄像式传感器，只能对左右股钢轨标准工作边的半断面轮廓进行测量，无法完成钢轨轮廓全断面测量。钢轨非标准工作边包含了丰富的数据信息，对钢轨磨耗计算基准选取、钢轨轮廓匹配、车辆振动补偿及道岔区域轨道几何参数计算等具有重要的参考价值。近年，随着计算机视觉测量技术的快速发展及视觉测量成本降低，国外相关研究人员针对钢轨半断面检测在轨形监控、钢轨磨耗计算、钢轨缺陷判定中所存在不足，加强了钢轨轮廓全断面动态测量技术方面的研究，研制了相关产品，其中有代表性的有意大利MERMEC公司、美国的ENSCO公司和KLDLABS公司。

针对我国轨道检测技术现状，结合国外轨道检测最新研究进展以及国内轨道检测车研制背景，本文对影响钢轨轮廓全断面检测精度的关键技术问题进行研究，主要包括钢轨轮廓全断面测量中多视角条件下不同视觉传感器全局标定及考虑车辆蛇形运动的钢轨轮廓测量数据多自由度振动补偿；梳理形成系统的钢轨轮廓全断面检测技术方法；将研究方法应用于现场钢轨轮廓全断面动态测量中，为提高钢轨全断面轮廓检测精度提供理论方法和技术手段。

1 测量原理

采用激光摄像技术进行钢轨轮廓全断面动态测量，系统检测原理见图1。要实现左右股钢轨轮廓全断面测量，至少需使用4组激光摄像式传感器，每组由1台摄像机和1台线结构光源构成，其空间布置见图1。同一股钢轨，紧贴车轮踏面的一侧称钢轨内侧，远离车轮踏面的另一侧称钢轨外侧。受车底安装空间限制及视角影响，要实现钢轨轮廓全断面测量，须在同一股钢轨内外侧的不同视角条件下对称安装2组激光摄像式传感器。安装时，须保证内外侧激光摄像式传感器投射的结构光平面重合，见图2。

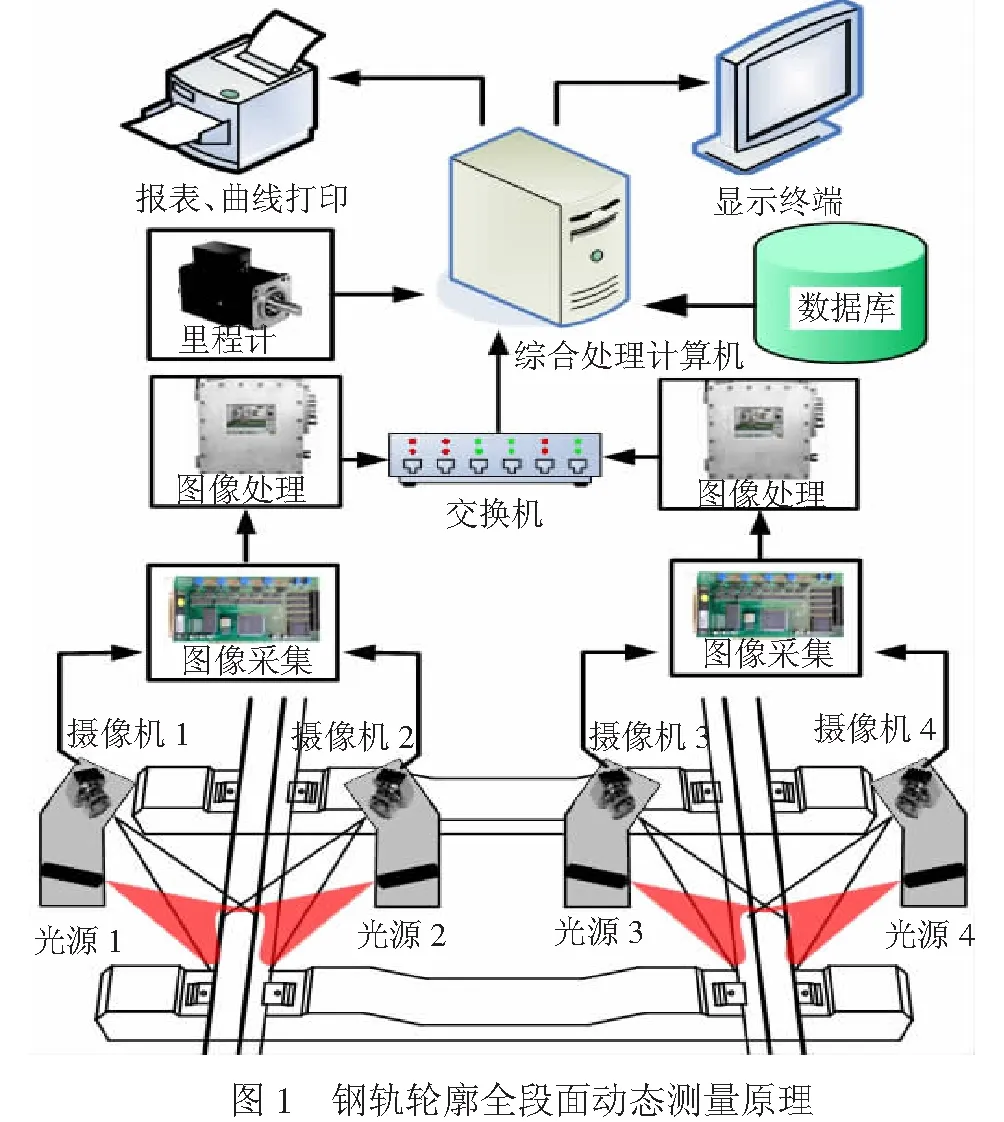
测量时，内外侧激光摄像式传感器投射的结构光平面与钢轨相交，在钢轨表面形成一条包含钢轨轮廓信息的激光光条曲线。旁侧摄像机与结构光平面呈一定角度拍摄钢轨激光轮廓图像，基于激光三角测量原理，实现钢轨轮廓检测。检测过程

Step1车轴转动带动光电里程计旋转输出脉冲信号，检测系统采集光电脉冲信号后，作为触发信号同时传输给左右股钢轨轮廓检测的4台摄像机，完成同一时刻钢轨激光光条图像采集。

Step2图像采集系统获取钢轨轮廓图像后，实时传输给图像处理系统，进行相应的钢轨激光光条特征提取、激光光条坐标换算和重合区域坐标融合，得到完整钢轨断面轮廓数据。

Step3钢轨全断面轮廓数据通过车载局域网络实时传输给综合处理计算机。综合处理计算机将实时获取的钢轨轮廓与标准钢轨轮廓进行对比和匹配，通过轨腰曲线固有特征信息，计算车辆振动量，并依此进行振动补偿。

Step4综合处理计算机结合软件中存储的线路数据库信息和光电里程计实时定位信息，将钢轨轮廓最终测量数据与上述空间信息相结合，形成检测数据记录，写入存储磁盘，同时在显示器和打印机中同步显示和打印。

2 测量模型建立

实现钢轨轮廓全断面高精度动态测量，需对钢轨轮廓测量视觉传感器进行高精度标定。以图2中单股钢轨轮廓全断面测量中内外侧相邻视觉传感器为例，介绍其标定方法。

钢轨轮廓测量视觉传感器标定原理见图3，各参数及符号定义见表1。钢轨轮廓测量视觉传感器标定，即采用合适的计算方法求取摄像机内部参数、相邻摄像机外部参数和结构光平面方程系数。采用二维平面靶标对钢轨轮廓测量视觉传感器进行在线标定，主要包括：

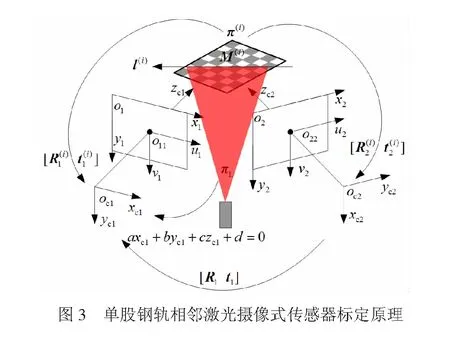
Step1自由移动平面靶标，经过i次移动后的靶标平面记为π(i)，确保靶标平面π(i)在左右摄像机中能够同时清晰成像后，固定靶标。

Step2为避免结构光对图像角点提取影响，关闭激光光源，分别调节左右摄像机曝光时间，使靶标平面π(i)能够在左右摄像机中同时清晰成像后，拍摄靶标平面π(i)在相邻摄像机中图像。

Step3保持Step2中靶标空间位置不变，结构光源通电，结构激光平面πL与靶标平面相交后，在π(i)上形成激光光条直线l(i)，调节摄像机曝光时间，使激光光条能够在左右摄像机中同时清晰成像后，相邻摄像机同时拍摄激光光条图像。

Step4移动平面靶标，重复Step1～Step3，左右摄像机分别拍摄同一靶标在至少3个不同空间位置处的图像。

Step7综合摄像机内部参数Ak、相邻摄像机外部参数[R1t1]、激光平面方程，建立钢轨轮廓全断面视觉测量模型。

表1 参数及符号定义

注：下标k表示第k个摄像机。

2.1 摄像机内部参数Ak标定

( 1 )

( 2 )

( 3 )

( 4 )

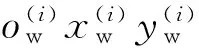
( 5 )

将Ak带入式( 5 )，展开后可得

( 6 )

将式( 6 )带入式( 4 )，通过空间中3组不同靶标平面坐标数据，求出摄像机内部参数矩阵Ak中未知变量[19]

( 7 )

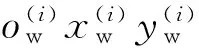
( 8 )

上述标定过程采用的是摄像机理想成像模型，实际标定过程中镜头存在一定非线性畸变。引入镜头畸变因子δu(x,y)、δv(x,y)，其计算公式[17-18]

( 9 )

式中：r2=u2+v2。

(10)

展开式(10)，可得

(11)

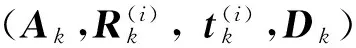
(12)

2.2 相邻摄像机外部参数标定

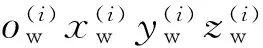
(13)

(14)

(15)

用式(15)求解oc1xc1yc1zc1、oc2xc2yc2zc2外部参数矩阵，结果为[22]

2.3 激光平面方程标定

(17)

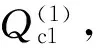
(18)

展开式(18)，得到激光平面方程一般表示形式axc1+byc1+czc1+d=0。[abcd]T即为获取的激光平面方程标定系数。

2.4 钢轨轮廓全断面测量模型建立

钢轨轮廓全断面测量时，激光平面内任意一点Q在摄像机坐标系oc1xc1yc1zc1中记为Qc1，在摄像机坐标系oc2xc2yc2zc2中记为Qc2，在各自摄像机中图像记为q1、q2。根据摄像机透视变换矩阵Ak，对钢轨轮廓测量中的内外侧摄像机建立成像模型

s1q1=A1Qc1

(19)

s2q2=A2Qc2

(20)

由2.2节中求得的相邻摄像机外部参数R1、t1，可知Qc2与Qc1的关系

Qc2=R1Qc1+t1

(21)

钢轨轮廓测量时，钢轨激光轮廓图像坐标q1、q2可通过图像实时获取。将q1带入方程(19)，联立方程(18)、(19)，即可求取外侧钢轨激光轮廓在摄像机坐标系oc1xc1yc1zc1中坐标。同理，将内侧钢轨轮廓图像坐标q2带入方程(20)，联立方程(18)、(20)、(21)，可获取内侧钢轨轮廓在摄像机坐标系oc1xc1yc1zc1中坐标。将钢轨内外侧轮廓测量数据在同一坐标系下进行叠加，便可最终实现钢轨轮廓全断面测量。

3 振动补偿

轨道检测车动态行进中，安装于转向架上的视觉传感器跟随车辆一起发生随机振动。要实现钢轨轮廓高精度动态测量，必须进行车辆振动补偿[24-25]，见图5。轨道中心坐标系记为owxwywzw，绕owxw、owyw、owzw轴振动分别定义为浮沉振动、摇头振动、侧滚振动。

车辆振动存在多个自由度，且各方向振动相互耦合，很难直接测出。将车辆不同类型振动按不同基准坐标轴进行正交分解，通过钢轨轨腰中包含的固有特征信息，计算车辆振动在不同方向的参量，以此为基础进行车辆振动补偿。

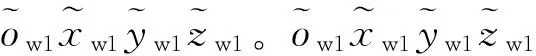
3.1 车辆振动对钢轨轮廓测量误差影响

车辆绕基准坐标系中ow1xw1、ow1yw1和ow1zw1坐标轴发生振动，对钢轨轮廓测量影响见图7。

(22)

(23)

(24)

3.2 振动补偿方法

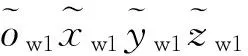
钢轨轨头区域与车轮踏面接触，有磨损，无法作为测量基准。轨腰作为轮轨非接触区域，适合作为车辆振动补偿基准。钢轨轨腰由半径不等的大小圆弧圆顺连接而成[26]，可选择轨腰处不同滚动圆的圆心作为振动补偿计算特征点。补偿计算原理见图8。设第k个摄像机测量所得钢轨轮廓数据中，轨腰处大圆弧记为AkBk，小圆弧为BkCk，Bk为AkBk与BkCk切点，大圆圆心和小圆圆心分别记为ok1、ok2，半径为r1、r2。

测量车辆振动带来的俯仰角θ1、偏航角θ2以及滚转角θ3，需对轨腰处的大圆弧和小圆弧进行拟合。由仿射定理可知，圆经过仿射变换后会变成椭圆[27]。因此，振动条件下测量所得钢轨轮廓，轨腰处大圆弧和小圆弧并非标准圆弧，而是椭圆圆弧。本文利用椭圆圆弧中包含的振动信息，对车辆振动姿态进行测量。

车辆振动补偿计算方法的步骤为

Step1采用椭圆拟合算法，拟合振动状态下测量所得钢轨轮廓中轨腰处椭圆圆弧，求取椭圆圆弧对应的圆心坐标；

Step2将求得的椭圆圆心坐标与标准钢轨轮廓中圆心坐标进行对比，计算其与标准轨腰中圆弧圆心坐标偏差；

Step4将钢轨内侧摄像机2、3测量所得钢轨轮廓数据相结合，通过当前时刻ow1xw1、ow1yw1坐标轴相对初始时刻的变化，求取车辆滚转角θ3。

详细计算过程推演如下。

椭圆一般方程表达式为

f(a,x)=ax2+bxy+cy2+dx+ey+f=0

(25)

式中：a=[abcdef]；x=[x2xyy2xy1]。

椭圆圆心计算式

(26)

设第k个摄像机测量的钢轨轨腰大圆弧方程为fk1(ak1,x)，轨腰小圆弧方程为fk2(ak2,x)，大圆弧坐标点数量为N1，小圆弧坐标点数量为N2，可对第k个摄像机测量的钢轨轮廓数据建立关于大小圆弧方程待定系数(ak1,ak2)的拟合函数

F(ak1,ak2)=

(27)

通过椭圆拟合算法，可以精确求解椭圆方程系数ak1、ak2，带入式(26)，得大小椭圆圆心坐标。将钢轨内外侧大圆圆心与小圆圆心o11、o21和o12、o22作为特征点，对车辆振动中的俯仰角和偏航角进行求解。

(28)

(29)

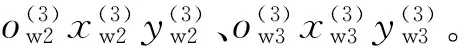
(30)

借助o21C和o31C，求得车辆滚转角为

(31)

4 试验

4.1 标定试验

图10为钢轨轮廓测量视觉传感器标定实物。钢轨轮廓测量视觉传感器安装于轨头内侧斜上方约400 mm处，同一股钢轨的内外侧摄像机光学测量中心距离约600 mm，单个视觉传感器测量范围约300×450 mm2。每个视觉传感器由MICROVIEW公司的MVC1000SAM_GE60型摄像机(分辨率1 280×1 024像素)、KOWA公司的LM12NCL型镜头及Z_LASER线型激光器组成。选用棋盘格靶标作为标定物，棋盘格靶标精度为0.005 mm。

内外侧钢轨轮廓测量视觉传感器获取同一靶标在6个不同方向图像，见图11。保持靶标空间位置不变，获取靶标平面与激光平面相交后所得激光光条图像，见图12。

采用棋盘格角点亚像素提取算法，精确提取图11中棋盘格角点坐标[28]；同理，采用激光光条中心亚像素提取算法[29-31]，精确提取图12中棋盘格靶标平面与激光平面相交所得激光光条图像坐标。从图11、12中提取的内外侧钢轨轮廓测量视觉传感器标定计算数据，见图13。

采用2.1节中摄像机内外部参数分离计算方法，求得钢轨内外侧摄像机内部参数Ak、Dk及标定靶标平面与摄像机坐标系外部参数矩阵，结果见表2、表3。

借助表2、表3中标定结果及第2节中标定计算方法，求得相邻摄像机外部参数及激光平面方程

(32)

xc1+0.018yc1-0.27zc1+169.34=0

(33)

表2 摄像机内部参数标定结果

表3 靶标平面与摄像机坐标系外部参数标定结果

4.2 动态测量试验

实际线路中获取的内外侧钢轨轮廓图像，见图14。借助4.2节中求得的模型参数，对图14中钢轨轮廓图像进行处理，得到局部测量坐标系下钢轨轮廓测量结果，见图15(a)、15(b)。借助内外侧钢轨轮廓测量视觉传感器之间外部参数[R1t1]，将图15(a)、15(b)中检测结果转换到同一测量坐标系下，见图15(c)。最后，采用车辆振动补偿算法，对图15(c)中数据进行多自由度振动补偿，精确获取钢轨轮廓测量结果。

由于轨道检测车中的钢轨轮廓检测系统为动态测量系统，测量过程中受到车辆振动的影响，现场环境条件很难对其检测精度进行直接验证。动态条件下多次检测数据重复性是衡量动态检测系统检测性能优劣的一项重要指标。为验证振动补偿后钢轨轮廓测量精度，在同一段线路中采用不同速度等级对该线路钢轨轮廓进行动态测量，通过提取钢轨轮廓中磨耗检测数据和比较其重复性误差验证车辆振动补偿方法的有效性。钢轨磨耗测量基准见图15(d)，其中Wh、Wv分别为钢轨水平磨耗和垂直磨耗。

动态试验时，检测速度为20、40、60、80 km/h，测量1 000 m长线路内的Wh和Wv。测量系统每隔0.25 m输出一组钢轨磨耗数据。1 000 m长线路中，每项参数有4 000组数据，检测结果分别见图16。以20 km/h检测所得钢轨磨耗数据为基准，验证其余检测速度下钢轨磨耗检测数据与其重复性误差以及最大偏差，统计结果见表4。

由表4可知，同一段1 000 m长线路，以20 km/h测量钢轨水平磨耗、垂直磨耗数据为基准，其余速度下测量钢轨水平磨耗、垂直磨耗最大重复性误差eRMS分别为0.23、0.25 mm，其余速度下测量钢轨水平磨耗、垂直磨耗最大偏差emax分别为0.49、0.48 mm。

表4 钢轨磨耗测量误差

5 结论

(1) 详细推演了钢轨轮廓全断面视觉测量计算方法，建立了不同视角条件下的内外侧钢轨轮廓视觉传感器全局测量模型。

(2) 分析了动态检测中车辆多自由度振动对钢轨轮廓检测的影响，探明了车辆不同类型振动对钢轨轮廓测量误差影响规律，提出了基于正交分解的车辆多自由度振动解耦和补偿方法。

(3) 研制了钢轨轮廓全断面检测装置，并将该检测装置在实际线路中进行动态测量试验。试验表明，同一段1 000 m长线路，以20 km/h测量钢轨水平磨耗、垂直磨耗数据为基准，其余速度下测量钢轨水平磨耗、垂直磨耗最大重复性误差eRMS分别为0.23、0.25 mm，其余速度下测量钢轨水平磨耗、垂直磨耗最大偏差emax分别为0.49、0.48 mm。

参考文献：

[1] 温泽峰，金学松. 钢轨波浪形磨损研究[J]. 中国铁道科学，2007, 28(1): 136-138.

WEN Ze-feng, JIN Xue-song. Study on Rail Corrugation[J]. China Railway Science, 2007, 28(1): 136-138.

[2] 刑丽贤. 提速条件下钢轨伤损特点及钢轨伤损分类的研究[D]. 北京：中国铁道科学研究院，2008.

[3] 李伟，杜星，王衡禹，等. 地铁钢轨一种波磨机理的调查分析[J]. 机械工程学报，2013, 49(16): 26-32.

LI Wei, DU Xing, WANG Heng-yu, et al.Investigation into the Mechanism of Type of Rail Corrugation of Metro[J]. Journal of Mechanical Engineering, 2013, 49(16): 26-32.

[4] 刘月明，李建勇，蔡永林，等. 钢轨打磨技术现状和发展趋势[J]. 中国铁道科学，2014, 35(4): 29-37.

LIU Yue-ming, LI Jian-yong, CAI Yong-lin, et al. Current State and Development Trend of Rail Grinding Technology[J]. China Railway Science, 2014, 35(4): 29-37.

[5] 杜鹤亭，高林奎，张继元，等. 安全综合检测车的研制[J]. 中国铁道科学，2003，24(1)：49-53.

DU He-ting, GAO Lin-kui, ZHANG Ji-yuan, et al. Development of Comprehensive Safety Inspection Car[J]. China Railway Science, 2003, 24(1): 49-53.

[6] 魏世斌，刘玲萍，赵延峰，等. GJ-6型轨道检测系统[J]. 铁道建筑，2011，(11)：98-101.

WEI Shi-bin, LIU Ling-ping, ZHAO Yan-feng, et al. Track Inspection System of Type GJ-4[J]. Railway Engineering，2011, (11):98-101.

[7] 杨强，林建辉，丁建明，等. 基于二维激光位移传感器和遗传算法的钢轨磨耗动态检测系统[J]. 中国铁路，2012，(6)：85-88.

YANG Qiang, LIN Jian-hui, Ding Jian-ming, et al. Rail Wear Dynamic Measurement System Based on 2D Sensor and Genetic Algorithm[J]. China Railways, 2012,(6): 85-88.

[8] 张海洋，王平，钱丽华. 激光测距仪在高速道岔钢轨断面测试中的应用研究[J]. 铁道建筑，2009，(4)：102-103.

ZHANG Hai-yang, WANG Ping, QIAN Li-hua. Study on Laser Ranging Sensor Applying in High Speed Turnout Rail Profile Dynamic Measurement[J]. Railway Engineering, 2009,(4): 102-103.

[9] 华长权，寇东华，付石林，等. 几种钢轨磨损检测方法和仪器的对比分析[J]. 中国铁路，2013，(4)：67-70.

HUA Chang-quan, KOU Dong-hua, FU Shi-lin, ea al. Several Rail Wear Instrumentation and Measurement Approach Comparison[J]. China Railway, 2013,(4):67-70.

[10] LI G X, WANG C L, LIU J H, et al. Dynamic Rail-wear Inspecting System Based on Machine Vision[C]//IEEE Conference on Industrial Electronics and Applications. Harbin： IEEE Press, 2007: 1-4.

[12] POPOV D V, RYABICHENKO P B, KRIVOSHEINA E A. Calibration of the CCD Photonic Measuring System for Railway Inspection[C]// Proceeding of SPIE. Bellingham: SPIE Press, 2005: 1-9.

[13] MAURO M, MATTEO T, GABRIELE M. Archimede--the First European Diagnostic Train for Global Monitoring of Railway Infrastructure[C]//IEEE Intelligent Vehicle Symposium. Parma: IEEE Press, 2004: 522-526.

[14] SUN J H, LIU Z, ZHAO Y T, et al. Motion Deviation Rectifying Method of Dynamically Measuring Rail Wear Based on Multi-line Structured-light Vision[J]. Optics & Laser Technology, 2013, 50(9): 25-32.

[15] LIU Z, SUN J H, WANG H, et al. Simple and Fast Rail Wear Measurement Method Based on Structured Light[J]. Optics and Lasers in Engineering, 2011, 49(11): 1343-1351.

[16] 占栋，于龙，肖建，等. 轨道检测中激光摄像式传感器标定方法研究[J]. 机械工程学报，2013, 34(7): 1625-1633.

ZHAN Dong, YU Long, XIAO Jian, et al. Study on Vehicle Vibration Compensation in Railway Track Profile Inspection[J]. Chinese Journal of Scientific Instrument, 2013, 34(7): 1625-1633.

[17] WENG J Y, PAUL C, MARC H. Camera Calibration with Distortion Models and Accuracy Evaluation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1992, 14(10): 965-980.

[18] WANG J H, SHI F H, ZHANG J, et al. A New Calibration Model of Camera Lens Distortion[J]. Pattern Recognition, 2008, 41(2): 607-615.

[19] ZHANG Z Y. A Flexible New Technique for Camera Calibration[J]. IEEE Transaction on Pattern Analysis and Machine Intelligence, 2000, 22(11): 1330-1344.

[20] 张光澄. 非线性最优化计算方法[M]. 北京:高等教育出版社，2005.

[21] 龚纯，王正林. 精通MATLAB最优化计算方法[M]. 北京：电子工业出版社，2012.

[22] 张广军. 视觉测量[M]. 北京：科学出版社，2008.

[23] ZHOU F Q, ZHANG G J. Complete Calibration of a Structured Light Stripe Vision Sensor Through Planar Target of Unknown Orientations[J]. Image and Vision Computing, 2005, 23(1): 59-67.

[24] 严隽耄.车辆工程[M]. 北京：中国铁道出版社，2009.

[25] 占栋，于龙，邱存勇，等. 钢轨轮廓测量中的车体振动补偿问题研究[J]. 仪器仪表学报，2013, 34(7): 1625-1633.

ZHAN Dong, YU Long, QIU Cun-yong, et al. Study on vehicle Vibration Compensation in Railway Track Profile Inspection[J].Chinese Journal of Scientific Instrumentation, 2013, 34(7): 1625-1633.

[26] 中国国家质量监督检验检疫总局，中国国家标准化管理委员会. GB2825—2007 铁路用热轧钢轨[S]. 北京：中国质检出版社，2008.

[27] HARTLEY R, ZISSERMAN A. Multiple View Geometric in Computer Vision[M]. 2nd ed.New York: Cambridge University Press, 2003.

[28] HARRIS C, STEPHENS M. A Combined Corner and Edge Detector[C] //Proceedings of the 4th Alvey Vision Conference. Paris: SPIE Press, 1988:147-151.

[29] 胡坤，周富强，张广军. 一种快速结构光条纹中心亚像素精度提取方法[J]. 仪器仪表学报，2006，27(10)：1326-1329.

HU Kun, ZHOU Fu-qiang, ZHANG Guang-jun. Fast Extrication Method for Subpixel of Structured-light Stripe[J]. Chinese Journal of Scientific Instrument, 2006, 27(10): 1326-1329.

[30] 贾倩倩，王伯雄，罗秀芝. 光切法形貌测量中光条中心的亚像素提取[J]. 光学精密工程，2010，18(2)：390-396.

JIA Qian-qian, WANG Bo-xiong, LUO Xiu-zhi. 3D Surface Measurement Based on light Sectioning Method[J]. Optics and Precision Engineering, 2010, 18(2):390-396.

[31] 吴家勇，王平江，陈吉红. 基于梯度重心法的线结构光中心亚像素提取方法[J]. 中国图象图形学报，2009，14(7)：1354-1360.

WU Jia-yong, WANG Ping-jiang, CHEN Ji-hong. Method of Linear Structured-light Subpixel Center Position Extracting Based on Gradient Barycenter[J]. Journal of Image and Graphics, 2009, 14(7): 1354-1360.