超声波传感器接收信号强度非对称性分析及对策*

王 翥,崔晓志,侯春雷

(哈尔滨工业大学(威海)信息与电气工程学院,山东 威海 264209)



超声波传感器接收信号强度非对称性分析及对策*

王 翥*,崔晓志,侯春雷

(哈尔滨工业大学(威海)信息与电气工程学院,山东 威海 264209)

针对采用时差法测量流速时,超声波传感器顺、逆两向接收信号强度存在的非对称性、非均匀性问题,提出了一种改善超声波传感器性能的方法。根据超声波传感器的波束角、发声传感器与受声传感器的间距,分别计算出超声波沿着波束角中心线和外线到达受声传感器表面的时间,进而通过改进压电元件模块提出一种缩短信号分别沿着中心线和外线到达受声传感器表面时间差的超声波传感器设计方法。理论分析可知,该方法可以有效地改善接收信号强度非均匀、非对称性问题,提高了流量测量精度。

超声波传感器;波束角;时差法;非对称性

众所周知,超声波流量计是测量气体、液体等流体流量的装置,而超声波传感器是超声波流量计的关键件之一。采用时差法测量流体流速时,超声波在顺逆两向传输时,传播速度与流体速度有叠加,这样顺逆两向超声波传播时间就存在时间差,依此可以计算流体流速[1],进而得出流量值。目前,针对如何提高超声波传感器检测流体流速的精确度问题,国内外学者做了大量研究。文献[2-3]中分析了超声波信号发送波和回波的非线性和延迟特征,通过优化算法使时间差的测算进一步精确化,文献[4]中通过游标卡尺原理放大时间差的计算,从而提高了测量的分辨率及精度,文献[5-7]中分别通过调整超声波发生装置的安装位置、锁相环跟踪功能和相控阵列技术以低噪声的影响,实现流速的精确测量,文献[8-9]中强调了管道中流速分布非均匀性对流速测量的影响并通过相应的参数模型提供流速误差补偿,进而提高超声波流量计的测量精度。但由于超声波传播具有指向性,即存在指向角,且在实际中存在层流与紊流的影响,则超声波到达接收面的中心和周边存在时间差。因此,便存在受声传感器接收信号强度的非均匀性与非对称性问题。

本文提出了一种改进方法,在现有传感器技术基础上,将压电元件分成两体结构,在不影响有效接收信号强度的前提下,改善了接收信号的均匀性、对称性,提高了信噪比,对保证超声波流量计的测量精确度具有显著意义。

1 流量计算原理

采用超声波传感器基于时差法测量流速的工作原理如图1所示。

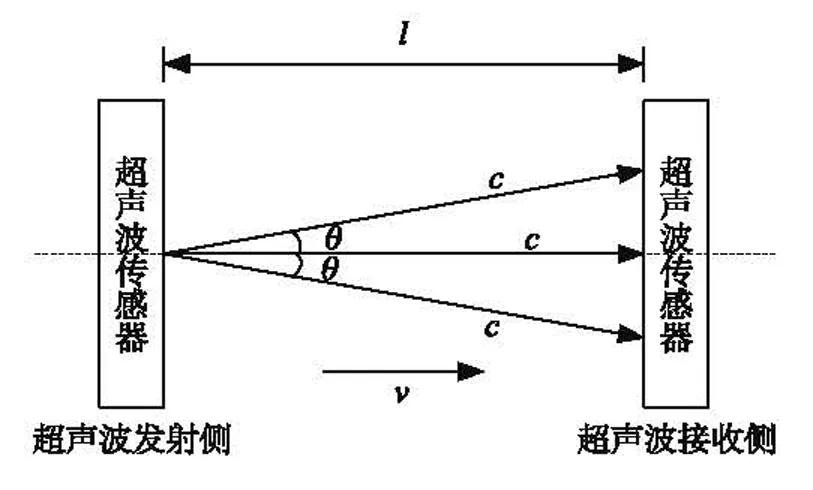
图1 超声波顺向传播

图1中超声波发声方向与流体流速方向一致(顺向),同时也存在超声波发声方向与流体流速方向不一致(逆向)的状态,在此不重复表示。理想状态下,设超声波传感器间距为l,超声波在流体中传播的波速为c,流体流速为v。超声波顺流方向传播时,超声波从发射侧到达接收侧的时间为t1,逆流方向传播时,超声波从发射侧到达接收侧的时间为t2,则:

顺逆两向超声波传播时间差:

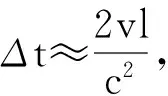
通过测得时间差可得到流体流速,进而计算出流体的流量值[10]。

2 目前技术存在的问题

2.1 超声波波束角

超声波发射波束形状如图2所示[11]。某一点发出的速度为c的超声波以一定指向角θ发射,超声波呈圆盘状向接收侧发射,且圆盘状的截面积由小到大。

图2 实际波束形状

2.2 理想状态下均匀性与对称性分析

理想状态是指流体在管道内的流速是一致的。设超声波沿顺流方向传播时,波在中心线传播的时间为t理0+,沿θ方向传播的时间为t理θ+,则:

因为c≫v,所以理想状态下超声波顺流方向传播时,超声波沿中心线和以一定指向角方向传播到达接受面的时间差t理+为:

(1)

设超声波沿逆流方向传播时,依据式(1)计算原理可知,超声波沿中心线和以一定指向角方向传播到达接受面的时间差t理-为:

(2)

由式(1)、式(2)比较可知:t理+>t理-。

说明超声波与流速方向一致时,超声波分别沿中心线与以一定指向角方向传播到达接受面的时间差,大于超声波与流速方向不一致时,超声波分别沿中心线与以一定指向角方向传播到达接受面的时间差。也就是说,当管道内流体流动时,接收到的超声波存在非均匀性和非对称性。

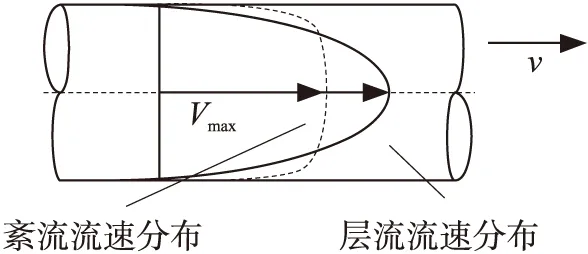
图3 层流与紊流流速分布

2.3 非理想状态下均匀性与对称性分析

对于非理想状态,液体存在粘滞性而具有两种流动形态。液体质点做有条不紊的运动、彼此不相混掺的形态称为层流;液体质点做不规则运动、互相混掺、轨迹曲折混乱的状态称为紊流。图3为层流与紊流流速分布比较,vmax为轴心线流速,v表示面流速。两者之间的关系为:

层流:v/vmax=0.5

紊流:v/vmax=0.75-0.9(取0.825进行简化计算)

2.3.1 层流状态下均匀性与对称性分析

设超声波沿顺流方向传播时,依据式(1)计算原理可知,超声波沿中心线和以一定指向角方向传播到达接受面的时间差t层+为:

(3)

设超声波沿逆流方向传播时,依据式(2)计算原理可知,超声波沿中心线和以一定指向角方向传播到达接受面的时间差t层-为:

(4)

式(3)、式(4)比较可知:t层+>t层-。

2.3.2 紊流状态下均匀性与对称性分析设超声波沿顺流方向传播时,依据式(1)计算原理可知,超声波沿中心线和以一定指向角方向传播到达接受面的时间差t紊+为:

(5)

声波沿逆流方向传播时,依据式(2)计算原理可知,超声波沿中心线和以一定指向角方向传播到达接受面的时间差t紊-为:

(6)

式(5)、式(6)比较可知:t紊+>t紊-。

由上述分析得知:

t理+>t理-,t层+>t层-,t紊+>t紊-

可见,无论流体流速方向与超声波传输方向是否一致,超声波到达接收侧的中心与周边区域的时间都会存在一个时间差。即:因为存在指向角θ,所以沿中心线方向的超声波到达时间要短于超声波到达周边区域的时间,且顺向时间差大于逆向时间差。

这样,就存在以下两个问题:①超声波传感器接收的能量不够集中,主要原因是中心部位与周边部位存在接收信号强度的差异[12]。同时,存在接收信号强度的非均匀性,这会降低接收信号的信噪比;②顺、逆两向都存在非均匀性,并且顺、逆两向的非均匀性不一致,这就造成了两个传感器接收信号强度的非对称性,直接影响信号发生电路与信号接收电路处理信号的效果。

以上两个问题都影响到流量检测的精确度。

3 数据分析与改进措施

实验环境和条件:室内温度15 ℃～35 ℃,相对湿度25%～75%,大气压86 kPa～106 kPa,流量表口径为DN20,超声波传感器的谐振频率为1 MHz,传感器直径14 mm,厚度2.2 mm,超声波在水中波速1 500 m/s,传感器间距62 mm。则:

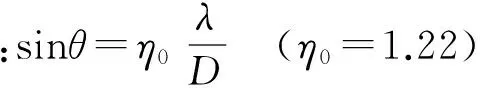
为了说明问题,本文以极端实验条件为例,即忽略中间状态,仅分析最大夹角状态。依据计算得知:cos7.5°=0.9914。

计算3种状态时间差。

比较可知:

Δt层+>Δt紊+>Δt理+>Δt理->Δt紊->Δt层-

层流比紊流状态下的时间差更明显。为便于叙述,采用特征更为明显的层流来说明接收信号时间差、接收信号强度和流体流速的关系。图4是顺逆两向接收信号强度非对称性与非均匀性的说明图。

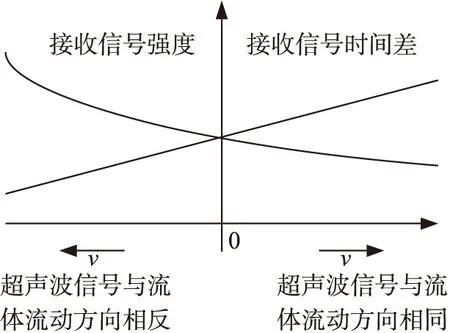
图4 信号强度说明图

直线表示接收信号时间差与流体流速之间的关系,曲线表示接收信号强度与流体流速之间的关系。直线的物理意义是:最左侧表明超声波到达接收面的时间差最小,最右侧表明超声波到达接收面的时间差最大。曲线的物理意义是:最左侧表明超声波接收面接收信号强度最大,最右侧表明超声波接收面接收信号强度最小。

从上述分析可知,产生顺逆两向超声波到达接收侧传感器时间差的主要因素是因为指向角θ较大。

针对现有技术的不足之处,本文提出的改进方法是:将现有结构的压电元件分为压电元件模块与虚拟压电元件模块,压电元件模块设置在外环,虚拟压电元件模块设置在内环,虚拟压电元件不具有压电效应。如图5所示。

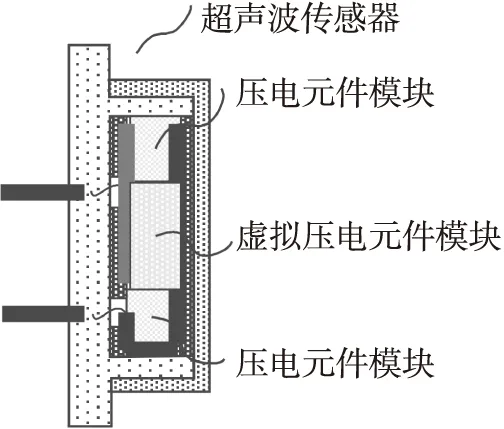
图5 改进后超声波传感器

因为压电元件模块的内外径之差远远小于压电元件外径,这就将有效接收信号的角度限制在很小的一个范围内,进而减小了顺逆两向超声波信号到达接收侧的时间差,大大改善了接收信号的非均匀性、非对称性,提高了信噪比。同时,将外环作为压电元件模块,保证了超声波信号的接收面积,也就保证了接收信号的强度。

本文以最大值与最小值之差除以流速作为相对偏差量来说明该改进方法的优越性。如表1,在全流速段内选择10个测量点作为对比数据。

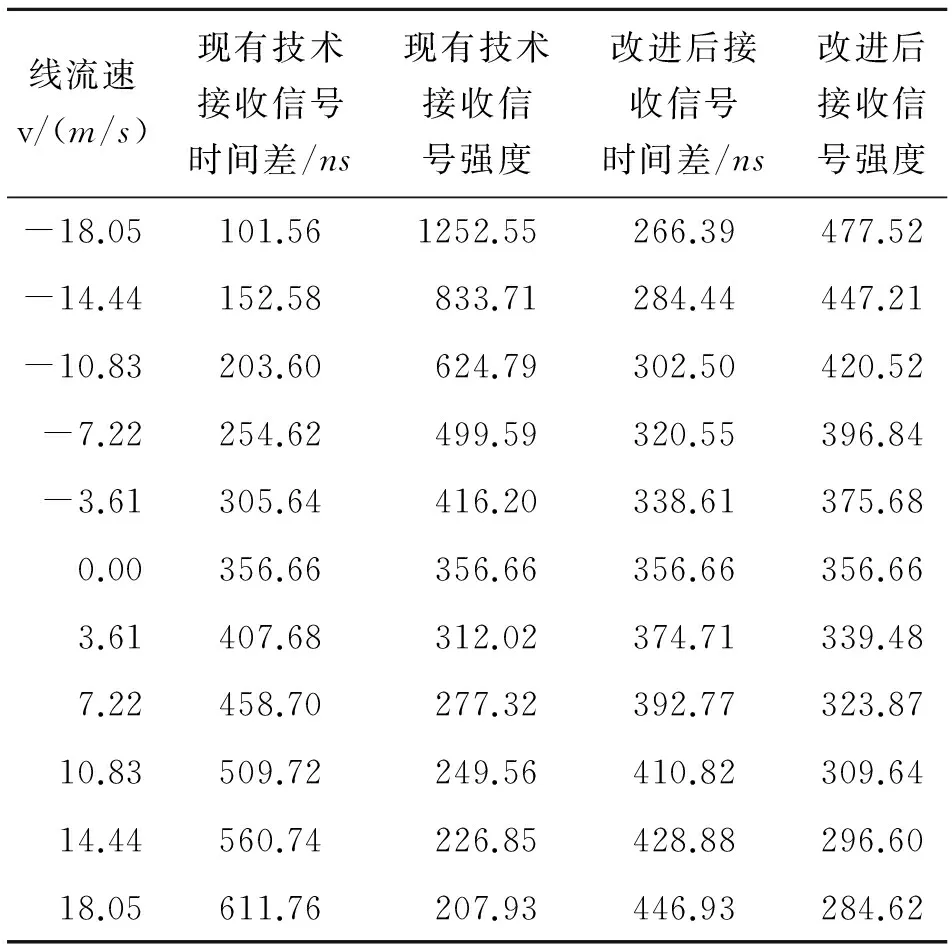
表1线流速与时间差、信号强度数据对比表

为便于对比,本文把流速为零的接收信号时间差与接收信号强度等值依据表1得对比曲线,如图6所示。

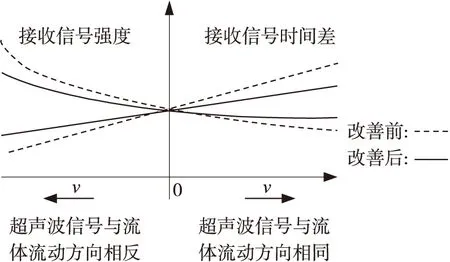
图6 改善前后线流速与时间差、信号强度数据对比曲线

由表1和图6可知。

现有技术接收信号时间差的相对偏差量:

(611.76-101.56)/356.66≈143%

改善后接收信号时间差的相对偏差量:

(446.93-266.39)/356.66≈51%

现有技术接收信号强度的相对偏差量:

(1252.55-207.93)/356.66≈293%

改善后接收信号强度的相对偏差量:

(477.52-284.62)/356.66≈54%

可以看出,改善后接收信号时间差的相对偏差量由143%降低到51%,其均方差由161.34ns降到57.08ns,接收信号强度的相对偏差量由293%降低到54%,其均方差由304.96降到60.47。表明,该方法大大改善了接收信号时间差与强度的对称性和均匀性,流量检测精确度可得到大幅度的改善。

4 结论

现有的超声波传感器测量液体流量时存在接收侧超声波传感器接收信号强度非均匀、非对称问题,且影响流量测量精度。本文所提出的改进方法的有益效果是:将现有技术的压电元件分解为压电元件模块和虚拟压电元件模块,在不影响有效接收信号强度的前提下,改善了接收信号的均匀性、对称性,提高了信噪比,对保证超声波流量计的精确度具有显著意义。

[1]李艳.一种新型超声波流量传感器[J].仪表技术与传感器,2012(7):12-13.

[2]宋寿鹏,阙沛文.超声信号的非线性行为及应用[J].传感技术学报,2007,20(1):128-131.

[3]徐斌.一种考虑起振延迟的低频超声波短距高精度测量校准方法[J].传感技术学报,2013,26(5):666-669.

[4]刘晓宇,杨江.时间比例放大技术在超声波流量计中的应用[J].传感技术学报,2007,20(2):454-457.

[5]Wang B,Cui Y,Liu W,et al.Study of Transducer Installation Effects on Ultrasonic Flow Metering Using Computational Fluid Dynamics[J].Advanced Materials Research,2013,629:676-681.

[6]Chen Y,Huang Y,Chen X.Acoustic Propagation in Viscous Fluid with Uniform Flow and a Novel Design Methodology for Ultrasonic Flow Meter[J].Ultrasonics,2013,53(2):595-606.

[7]Fukumoto T,Tsukada K,Ihara T,et al.A Study of Phased Array Ultrasonic Velocity Profile Monitor for Flow Rate Measurement[C]//2013 21st International Conference on Nuclear Engineering.American Society of Mechanical Engineers,2013:V006T16A051-V006T16A051.

[8]Iooss B,Lhuillier C,Jeanneau H.Numerical Simulation of Transit-Time Ultrasonic Flowmeters:Uncertainties Due to Flow Profile and Fluid Turbulence[J].Ultrasonics,2002,40(9):1009-1015.

[9]Mandard E,Kouamé D,Battault R,et al.Transit Time Ultrasonic Flowmeter:Velocity Profile Estimation[C]//Ultrasonics Symposium,2005 IEEE.IEEE,2005,2:763-766.

[10]王新峰,熊显潮,高敏忠.超声波流量计测量流体声速的实验方法[J].物理学报,2011,60(11):114303-114303.

[11]中国机械工程学会无损检测分会超声波检测.超声波检测[M].机械工业出版社,2005:34-36.

[12]赵爱荣,陈雨,刘丽,等.埋入式压电陶瓷厚度对激励声能影响的有限元分析[J].传感技术学报,2014(2):178-183.

Analysis and Countermeasures to the Problem of Ultrasonic Sensor Receives the Ultrasonic Signal Asymmetric*

WANGZhu*,CUIXiaozhi,HOUChunlei

(Harbin Instituteof Technology at Weihai,School of Information and Electrical Engineering,Weihai Shandong 264209,China)

Ultrasonic sensor receives the ultrasonic signal downstream and upstream when measuring the flow rate with the time difference method.However the received signal strength is irregular and asymmetrical.For the problem,a modified method to improve the performance of ultrasonic sensor is presented.According to the beam angle and the spacing of sending-side and receiving-side,the time arriving at the surface of ultrasonic sensor along the center and perimeter is calculated,respectively.Then,there is time difference existing when ultrasonic reaches the surface of the receiving-side sensor along the center and perimeter.To shorten it,this paper proposes a design method of ultrasonic sensor by improving the piezoelectric element structure of ultrasonic sensor.Theoretical analysis shows that the modified method can not only effectively improve the problem of irregularly and asymmetrically received signal strength,but also increase the accuracy of flow measurement.

ultrasonicsensor;beamangle;timedifferencemethod;asymmetrical

王 翥(1963-),男,哈工大(威海)信电学院教授。研究方向为无线传感器网络及网络化测控技术、传感器及应用技术,wangzhu@hit.edu.cn;

崔晓志(1990-),哈工大(威海)信电学院硕士研究生。研究方向为超声波传感器及在流量检测中的应用技术。

项目来源:山东省科技发展计划项目(2012GGX10110)

2014-09-29 修改日期:2014-11-07

C:7230

10.3969/j.issn.1004-1699.2015.01.015

TB552

A

1004-1699(2015)01-0081-05