一种基于广义回归神经网络的超声波流量传感器系数求解方法

陈子静,朱小良

(东南大学能源与环境学院,南京 210096)



一种基于广义回归神经网络的超声波流量传感器系数求解方法

陈子静,朱小良*

(东南大学能源与环境学院,南京 210096)

为了解决和提高不稳定流场条件下的超声波流量传感器的测量精度问题,文章将广义回归神经网络引入到流量传感器系数获取当中,并通过建立流量传感器系数模型和样本输入训练,获得了较为准确的流量传感器系数和较高的测量精度,从而验证了本方法对超声波流量传感器在不稳定流场中进行流量测量的可行性,具有总要的实际应用借鉴价值。

超声波流量计;流量传感器系数;广义回归神经网络;CFD

超声波流量计与传统流量计相比,具有不影响流场、无可动部件、无压力损失、测量范围宽、以及在管内湍流充分发展条件下测量精度高等优点,其中最为重要的是可用于大口径管道流量的测量,并能够保持较高的精度。目前,超声波流量传感器已广泛应用到国内外大型电站流量测量中。

超声波流量传感器测量的是超声波传播途径上的线平均流速,经计算后,得到截面平均流速,然后得到流量,从线平均流速变换为截面平均流速的过程,称为流量传感器系数修正[1-2]。现有文献记载的流量传感器系数K大多是在认为管道内湍流流动充分发展的理想情况下通过流体力学公式推导求得或者实验标定[3-4]。然而在实际的工程应用中,由于种种客观条件的限制,导致无法达到流场充分发展所需的直管段长度,管道内流态分布复杂,流量传感器系数K发生较大的变化,若用于不稳定流场条件下的流量测量,如在90°单弯管下游19D处的测量误差可以超过4%[5]。因此研究一种如何准确得到流量传感器系数K的求解方法,具有非常重要的工程应用价值。针对这一问题,本文在研究流场对流量传感器系数K影响的基础上,采用广义回归神经网络(GRNN)建立模型,利用CFD数据作为网络训练样本以及外推测试样本,对流量传感器系数K进行预测。

1 超声波流量测量基本方法

典型超声波流量测量系统原理如图1所示,在管道的上下游分别布置二只换能器A和B,设流体静止时,超声波传播速度为C,先测得顺流时由探头A发射的超声波到达探头B接收的时间Δt1,再测得由探头B逆流发射超声波到探头A接收的时间Δt2。在水流的作用下,声波沿正向传播时间Δt1小于逆向传播所经历的时间Δt2。

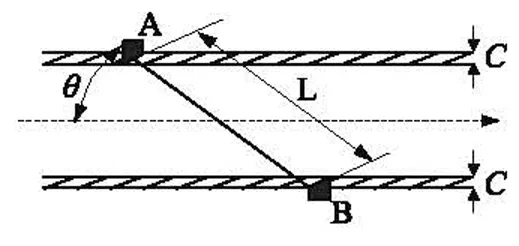
图1 超声波流量测量示意图

正向、逆向传播时间分别可以表示为[6]:

(1)

(2)

由(1)和(2)可以导出1条声波路径上的流体流速为:

(3)

为了得到实际面平均流速V,需要用流量传感器系数K对声道线平均流速Vz进行修正,本文定义流量传感器系数K为:

K=V/Vz

(4)

2 不同流场下流量传感器系数的大小

对于充分发展的湍流流动速度分布通常采用半经验的幂函数[7]

(5)

其中,r为距离管道中心的径向距离与管道半径之比,V(r)为流体距离轴心线r处沿轴线方向的面平均流速,Vm为流体沿轴心线上的流速,n为流速分布指数,取决于雷诺数和壁面粗糙度Kr。

对式(5)分别沿声学路径及圆管横截面进行积分可得:

(6)

(7)

从而得到充分发展湍流状态下流量传感器系数Km:

(8)

对于光滑管及粗糙管而言,可分别由Prandtl方程及Colebrook关系式求解n[8]:

n=2log10(Re/n)-0.8

(9.1)

n=1.74-2log10(Kr/R+18.7n/Re)

(9.2)

对于未达到充分发展状态的湍流流动,Salami通过计算模拟的方法得到了23种不同流体状态下的流速截面,并给出了不同流体状态下流速截面模型的3种表示形式,如式10所示[9]。

(10.1)

V(r)=Vm(1+zbsinθ)r≤b,0≤b≤1;

(10.2)

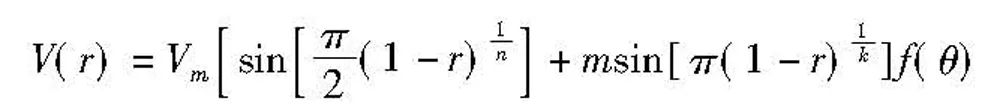
(10.3)

其中,b、z、k、m为特定常数,f(θ)为θ的函数,表征速度沿径向变化分量。

由式(10)可以看出,第1种表达形式非常易于积分,本文对(10.1)分别沿声学路径及圆管横截面进行积分,结果如下所示。

(11)

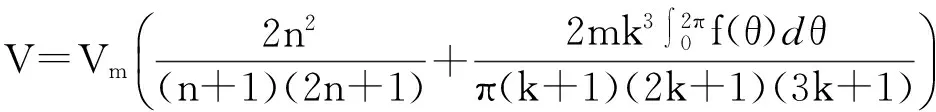
(12)

从而得到不稳定流场状态下流量传感器系数K:

(13)

当已知截面流速分布规律,即可确定唯一的n、k、m及f(θ),由式(13)可以确定流量传感器系数K的大小。

综上可知,无论在何种流场状况下,流量传感器系数K的大小均主要取决于测量截面处流速分布情况。在实际应用中,由于流场的复杂性以及不确定性,既无法获取实际流场的流速截面模型,而用理想流量传感器系数Km修正又必将产生较大偏差。因此为了得到在不稳定流场条件下流量传感器系数K的大小,首先需要对影响流场流速分布稳定性的因素进行研究分析。

3 影响流速分布稳定性因素

本文应用CFD流场仿真技术,以实际工程中常遇到的90°单弯管为例,对影响单弯管下游流场流速分布稳定性的因素进行了研究分析。仿真工作主要集中在以下3个方面:①改变管道入口初始流速,研究雷诺数Re变化对流速分布的影响;②改变测量截面与上游弯管之间的距离,研究上游相对直管段长度对流速分布的影响;③改变管道壁面粗糙度的大小,研究壁面粗糙度对流速分布的影响。

3.1 雷诺数Re对流速分布的影响

流体流过弯管往往会引起下游流场中含有二次流,而二次流强度主要取决于雷诺数Re和迪安数Dn两个无量纲常数。它们之间的关系如下所示[10]:

(14)

式中,d为管道的直径,R为管道的弯曲半径。

由上式可知,管道中二次流强度受雷诺数Re和管道曲率的控制。在管道曲率不变的前提下,管道内产生的二次流强度随雷诺数Re的增大而增大。图2给出了雷诺数分别为1×105和4×106时测量截面流速等值线分布情况。由图可知,截面流速等值线沿管道轴心的横向截面呈对称状态,雷诺数Re越大,二次流涡旋强度越大。

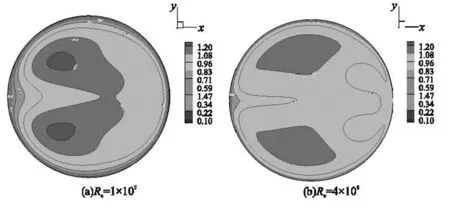
图2

3.2 上游相对直管段长度对流速分布的影响

现有文献记载弯管下游二次流强度随测量位置与弯管的距离的增加而明显减弱[11-12]。图3给出了单弯管下游 8D和20D截面处流速等值线分布情况,由图可知,上游相对直管段长度越长,二次流涡旋强度越弱,越有利于管内湍流流动达到充分发展状态。

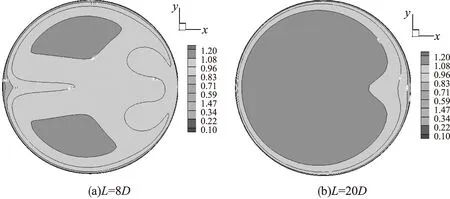
图3

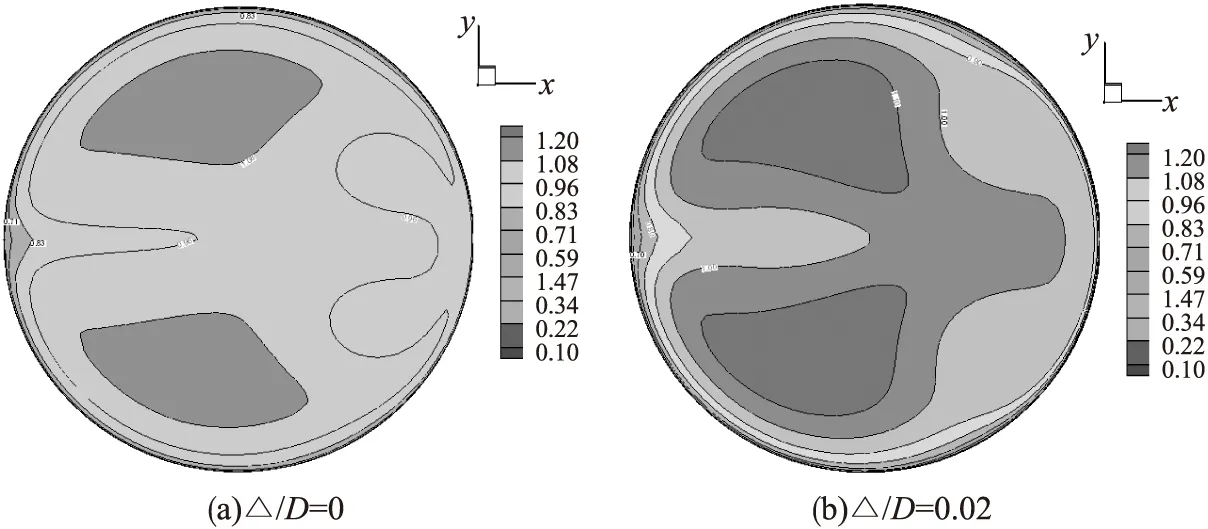
图4

3.3 壁面粗糙度对流速分布的影响

管道在长期的使用过程中由于腐蚀,磨损,生锈等原因,其壁面粗糙度会不断增大,当其粗糙度超过湍流粘性底层厚度时,将对整个管道内流速分布情况产生一定的影响。图4给出了壁面相对粗糙度为0和0.02时测量截面流速等值线分布情况,从图中可以看出,由于壁面粗糙度的增大,增大了近壁面附近流体流动的摩擦力,并使得边界能量消耗加剧,涡旋强度有所减弱。

4 广义回归神经网络基本结构

GRNN是一种径向基神经网络,该网络具有训练速度快、非线性映射能力强以及极强的容错性和鲁棒性等特点,在逼近能力,分类能力和学习能力方面均优于BP神经网络[13-14]。

广义回归神经网络(GRNN)由输入层、隐含层和输出层3层网络构成,具有一个径向基网络层和一个特殊的线性网络层,其结构如图5所示[15-16]。

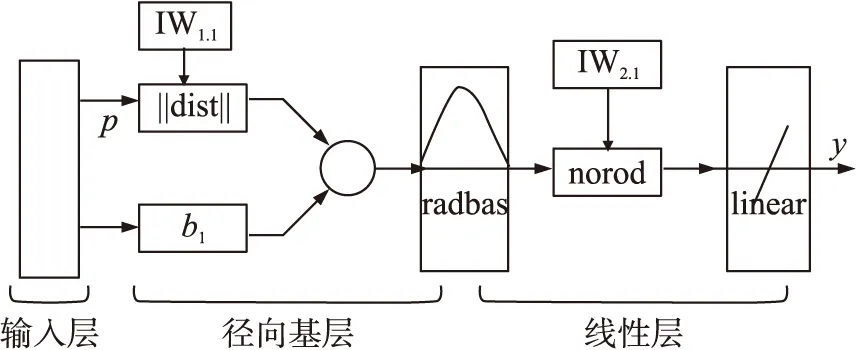
图5 GRNN模型结构

GRNN的第1层与用newrbe函数创建的RBF网络一样,其径向基神经元数目等于输入样本数目。其权值等于输入向量的转置:

IW=pT

(15)

所有径向基神经元的阀值为:

(16)

隐含层的传递函数通常采用高斯函数:

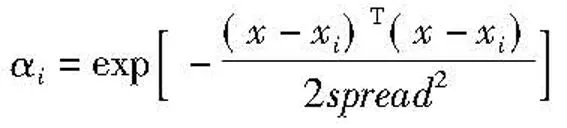
(17)

式中,x为网络输入变量,xi为第i个神经元对应的学习样本,αi为向量α2的第i个元素。spread为径向基函数的扩展系数,默认值为1.0。

网络线性输出层权函数为规范化点积权函数,将隐含层的输出与输出层的权值矩阵IW2,1作归一化点积运算后再作为权输入送入传递函数,计算网络的向量n2,即可得到网络的输出为:

α2=purelin(n2)

(18)

5 基于GRNN的流量传感器系数K修正模型

根据对影响流量传感器系数K因素的分析,这里分别取雷诺数、上游相对直管段长度和壁面粗糙度等3项指标作为流量传感器系数K的影响因子,并将其作为网络输入,以流量传感器系数K作为网络的输出,由此构建GRNN模型。为了获得更好的预测效果,在训练网络前,将所有输入、输出训练数据进行归一化处理,即使网络的输入和相应的输出处于[0,1]区间内。由于广义回归神经网络的学习完全取决于数据样本,因而在学习样本确定后,只需改变扩展系数spread即可调整网络训练效果。

5.1 训练样本数对预测精度的影响

为用尽量少的训练样本数目达到满意的预测精度,本文对训练样本数目n1分别为30、60和90进行了对比试验,预测样本数n2为20,spread为默认值。网络对训练样本的逼近误差及预测误差如图6所示。

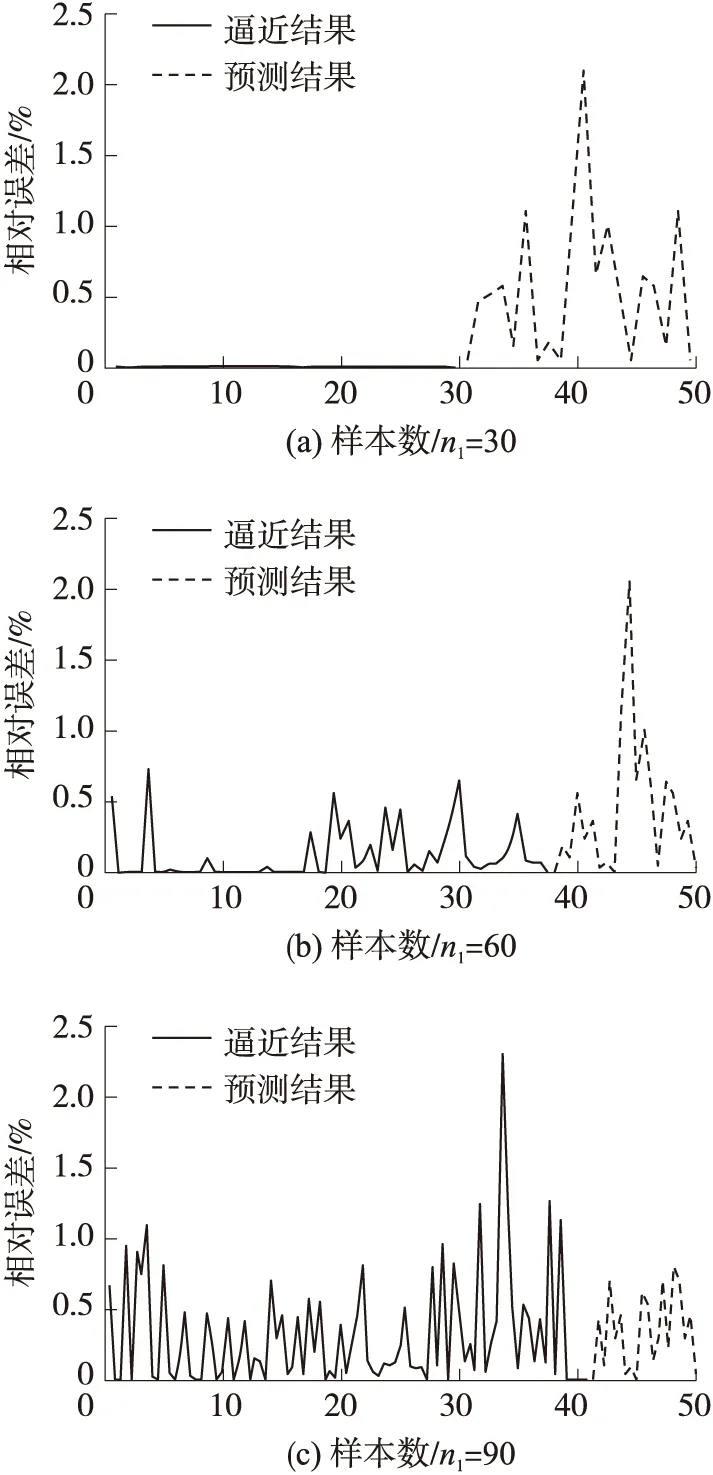
图6

由图6可知,随着网络训练样本数目增加,网络逼近误差逐渐增大,预测误差逐渐减小。当训练样本数n1分别为30、60和90时,网络逼近误差平均值分别约为0、0.12%和0.26%;预测误差平均值分别为0.68%、0.44%和0.29%。训练样本数n1为30与60时,预测误差波动幅度较大,误差最大值均超过2%;当训练样本数n1为90时,预测误差波动幅度较小,均在0.7%以内。显然当训练样本数n1为90时,网络既具有较好的逼近效果,又能够将预测误差控制在0.7%以内。综上考虑,本文取训练样本数选为90。

5.2 扩展系数对预测精度的影响

合理选择spread非常重要,spread值越大,其输出结果越光滑,但逼近误差较大,spread值越小,其逼近效果越好,但是逼近过程就越不平滑。为了确定一个最佳的spread值,本文分别设置spread为0.1、0.4、0.9、1.6和2.5,以检验不同的spread对网络逼近性能的影响,网络的逼近误差如图7所示;网络的预测误差如图8所示。由图可见,随着扩展系数的减小,误差也在不断减小,当扩展系数为0.4时,无论是逼近性能还是预测性能,误差都比较小,扩展系数再减小,误差基本不变。

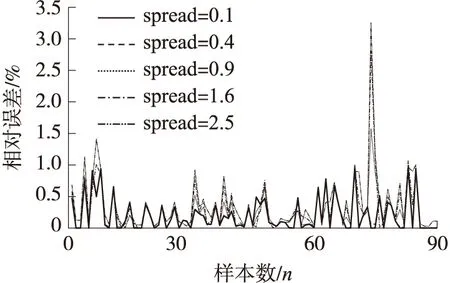
图7 逼近误差

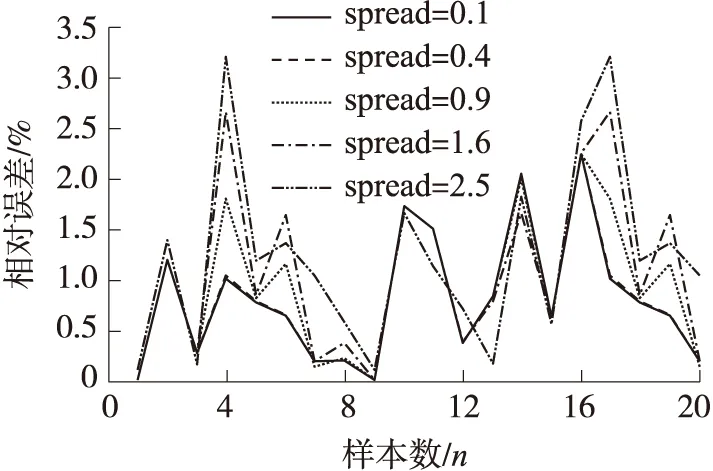
图8 预测误差

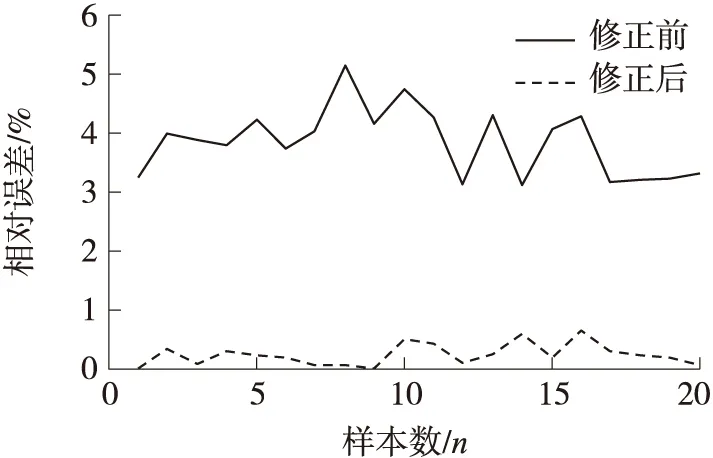
图9 修正前后误差对比

从误差的角度考虑,本文取扩展系数为0.4,此时流量传感器系数最大逼近相对误差为0.95%,逼近相对误差平均值为0.21%;流量传感器系数最大预测相对误差0.59%,预测相对误差绝对平均值为0.24%。根据以上拟合训练和外推预测的结果分析,可以看出,网络的拟合值和预测值与实际值比较接近,网络具有较好的预测能力。将预测结果与20个预测样本未修正前的相对误差进行对比,如图9所示。可以看出,经过GRNN训练之后,样本的相对误差发生了明显的减小,有效地提高了超声波流量传感器在不稳定流场条件下的测量精度。

6 结论

本文针对超声波流量传感器在不稳定流场条件下测量精度偏低问题,建立了基于广义回归神经网络的流量传感器系数求解模型。并以90°单弯管为例,通过CFD仿真分析了影响单弯管下游流场流速分布稳定性的各个因子,并将影响因子作为网络输入。研究结果表明,广义回归神经网络不仅结构简单,训练速度快,而且具有很好的预测效果,在不稳定流场条件下,超声波流量传感器能够得到较好的测量精度,从而有效地解决了超声波流量传感器在单弯管下游非稳定流场中测量精度低的问题。同时由于在其他阻流条件下,影响流速分布稳定性的因子与单弯管情况下基本相同,所以研究结果可以为其他阻流条件下超声波传感器系数的求解提供一定的指导作用。

[1]The American Society of Mechanical Engineers.ASMEPTC 18-2002:Hydraulic Turbines and Pump Turbines Performance Test[S].2002.

[2]Pamela I Moore,Gregor J Brown.Ultrasonic Transit-Time Flowmeters Modelled with Theoretical Velocity Profiles:Methodology[J].Meas Sci Technol,2000(11):1802-1811.

[3]Yeh T T,Espina P I.Special Ultrasonic Flowmeters forin-SituDiagnosis of Swirl and Cross Flow[J].Proceedings of Asme Fedsm,2001.

[4]Jung J C,Seong P H.Estimation of the Flow Profile Correction Factor of a Transit Time Ultrasonic Flow Meter for the Feedwater Flow Measurement in a Nuclear Power Plant[J].IEEE Transactions on Nuclear Science,2005,52(3):714-718.

[5]Terrance A Grimley,Edgar B Bowles.Industry Researchers Evaluate Ultrasonic Meter Performance[J].Measure Report,1998,81(12):35-42.

[6]王雪峰,唐祯安.超声波气体流量计的管道模型仿真和误差分析[J].仪器仪表学报,2009,30(12):2612-2618.

[7]Devin M Stoker.Ultrasonic Flow Measurement for Pipe Installations with Nonideal Conditions[J].Journal Ofirrigation and Drainage Engineering,2012,138:993-998.

[8]Dane H.Ultrasonic Measurement of Unsteady Gas Flow[J].Flow Measurement and Instrumentation,1998,8(34):183-190.

[9]Salami L A.Application of a Computer to Asymmetric Flow Measurement in Circular Pipes[J].Transactions of the Institute of Measurement and Control,1984(6):197.

[10]Lai Y G,Sor M C,Zhang H S.Turbulence Drivensecondary Flows in a Curved Pipe[J].The Oretical and Computational Fluid Dynamics,1991(3):163-180.

[11]Pruvost J,Legrend J.Numerical Investigation of Bend and Torus Flows,Part I:Effect of Swirl Motion on Flow Structure in U-Bend[J].Chemical Engineering Science,2004(59):3345-3357.

[12]Anselmet F,Ternat F,Amielh M.Axial Development of the Mean Flow in the Entrance Region of Turbulent Pipe and Duct Lows[J].Compies Rendus Mecanique,2009,337:573-584.

[13]陈娇,王永泓,翁史烈.广义回归神经网络在燃气轮机排气温度传感器故障检测中的应用[J].中国电机工程学报,2009,29(32):92-97.

[14]郭摇伟,张摇栋,李巨韬.改进型BP神经网络对电容称重传感器的非线性校正[J].传感技术学报,2012,25(10):1354-1360.

[15]孙艳梅,都文和,冯昌浩.基于蚁群聚类算法的RBF神经网络在压力传感器中的应用[J].传感技术学报,2013,26(6):806-809.

[16]王少福,张金磊,赵仕俊.广义回归神经网络的改进及在预测控制中的应用[J].微电子学与计算机,2009,26(6):32-36.

A Solution Method of Ultrasonic Flow Sensor Coefficient Based on Generalized Regression Neural Network

CHENZijing,ZHUXiaoliang*

(Energy and Environment Institute of Southeast University,Nanjing 210096,China)

In order to solve and improve the measurement accuracy of ultrasonic flow sensor in unsteady flow conditions,the general regression neural network was introduced to obtain the flow sensor coefficient.And through the establishment of the flow sensor coefficient model and the training of input samples,more accurate flow sensor coefficients and higher measurement accuracy were obtained.So the feasibility of this method for the flow measurement in non-ideal flow field conditions by ultrasonic flow sensors had been verified,and the practical reference value of this method also had been reflected.

ultrasonic flowmeter;flow sensor coefficient;generalized regression neural network;CFD

陈子静(1988-),男,江苏南京人,硕士研究生,从事热工过程流量检测方面的理论和应用研究,chen9025fighting@163.com;

朱小良(1965-),男,江苏常熟人,教授,从事热工测量理论和应用研究教学工作,101000522@seu.edu.cn。

2014-10-11 修改日期:2014-11-12

C:7820;7320W

10.3969/j.issn.1004-1699.2015.01.011

TK313

A

1004-1699(2015)01-0056-06