基于改进型ANFIS的磁致伸缩液位传感器温度补偿*

谢 苗,刘治翔,毛 君

(辽宁工程技术大学机械工程学院,辽宁 阜新 123000)



基于改进型ANFIS的磁致伸缩液位传感器温度补偿*

谢 苗1*,刘治翔1,毛 君1

(辽宁工程技术大学机械工程学院,辽宁 阜新 123000)

考虑到磁致伸缩液位传感器在温差变化大的环境中温漂现象严重,且产生温漂的多种因素与温漂的程度呈非线性关系,难以用数学模型表达等问题,建立基于改进型ANFIS的温度补偿系统。该系统采用附加动量算法不断修正ANFIS中的前题参数以避免采用梯度下降算法时易陷入局部极小,训练速度较慢等缺点,提高系统的忽略网络中微小变化的能力。为了验证该温度补偿系统的性能,将其与基于PSO-LSSVM模型和基于BP神经网络的温度补偿系统相比较。分析与实验结果表明,改进型ANFIS模型的温度补偿的最大误差为0.88%,平均误差为0.65%,远小于另外两种补偿方法。使用了改进型ANFIS的温度补偿方法具有较强的泛化能力,能够有效消除温度对磁致伸缩液位传感器的影响。

磁致伸缩液位传感器;温度补偿;改进型ANFIS;BP算法;神经网络;PSO-LSSVM模型

磁致伸缩液位传感器是一种新型的、高精度、高灵敏度、可用于传统液位传感器不能满足要求的工业场合[1-4],其广泛应用于航空航天、石油化工等工业领域[5-6],本文研究的磁致伸缩液位传感器应用于航空发动机滑油喷嘴流量试验器的计量系统中,因此其测量精度,对环境的适应性以及抗干扰能力更为重要。

在磁致伸缩液位传感器问题的研究上,颜庆伟[7]等人对传感器的工作原理、结构进行了介绍分析,设计了模块化的电路设计方法,并通过试验验证了这种电路设计方法具有较好的静态、动态特性,可以提高传感器的整体性能。代国前、王峥等人[8-9]运用了电磁学、材料力学等相关理论对磁致伸缩液位传感器的弹性波产生机理、信号检测机理等建立数学模型,并通过计算、实验对建立的模型进行验证,对后来学者研究提高传感器测量精度的方法提供了较好的理论依据和实验数据支持,具有积极的意义。但是这些学者对于温度对传感器的影响没有进行研究。陶若杰等[10]研究了一种双丝差动的新型结构,有效的降低了磁致伸缩位移传感器的噪声干扰,提高了测量的精度。李永波等[11]对分析了温度对传感器晶振频率、回波速率以及液体密度对传感器测量精度的影响,提出了可以消除上述影响的双辅助磁性浮子设计方法。但是这些提高传感器精度的方法均采用改动硬件结构的方式,不仅不易于实现,适应性不强,不能够对全程进行补偿、补偿电路易产生漂移等问题,而且对已生产的、已经投入使用的传感器无法采用该种方法进行修正。

依据上述问题,本文建立基于改进型自适应神经模糊推理系统的磁致伸缩液位传感器的温度补偿方法。该系统采用附加动量算法不断修正自适应神经模糊推理系统中的前题参数以避免采用梯度下降算法时易陷入局部极小,训练速度较慢等缺点,提高系统的忽略网络中微小变化的能力。结合理论分析与试验研究,对该种温度补偿方法进行了相关测试和分析。

1 传感器误差分析

1.1 磁致伸缩液位传感器工作原理

根据磁体的磁致伸缩原理设计出磁致伸缩液位传感器,由不会被磁化的不锈钢波导管、波导丝、内部装有磁铁的浮球以及电子信号处理装置等组成[12]。磁致伸缩液位传感器的工作原理如图1所示。

图1 磁致伸缩液位传感器工作原理

传感器工作时,装在传感器最上端的电子信号处理装置首先会将一个电流脉冲信号发送给磁致伸缩波导丝上,电脉冲会产生一个环形磁场,以光速传播,导波管会因为由电流脉冲信号产生的环形磁场遇到浮球内的磁铁时相互叠加而产生波导扭曲,并且会因此产生一个应变脉冲的超声波,超声波以一个固定的速率在波导管中向两端传播,当一端超声波遇到末端的衰减阻尼器时能量会被吸收,另一端超声波传到电子信号处理装置的接收器时会被转化为电流脉冲信号并被计时器采集,这样通过超声波的速度乘以发射电流脉冲与接收电流脉冲的时间差即可得到浮球的位置。

1.2 温度对传感器内部晶振的影响

通过对传感器工作原理了解可知,浮子的位置是由测量时的激励脉冲与返回脉冲的时间决定的,因此时钟晶振是决定传感器稳定性以及测量精度的重要因素,然而在被测液位温度变化较大时,晶振会产生温度漂移,随之带来的传感器测量的误差,可以使用温度漂移系数来表示晶振的温度漂移:

Ntm=kNtb

(1)

式中:Ntm为在t℃,进行测量时的脉冲数;Ntb为在标定温度下,进行测量时的脉冲数;k为晶振的温度漂移系数。

1.3 温度对回波速率的影响

磁致伸缩液位传感器的本质是使用时间值表示液位值,磁致扭转弹性波的回波速率为:

(2)

式中:ρb为波导丝的密度;Gb为波导丝的弹性模量。

可以看出,回波速率与波导材料的密度、应力、弹性模量等参数有关,而这些参数会随着温度变化产生明显的改变,因此上述回波速率公式适用于恒温下,温度变化不大的测量场合[13]。

1.4 温度对磁致伸缩液位传感器浮子的影响

本文研究的传感器的被测液体是航空滑油,其密度会随着温度变化而变化,通过实际的实验测量,二者变化曲线类似于抛物线,而密度的变化会使得同一个物体侵入该液体体积发生改变。由磁致伸缩液位传感器的工作原理得知传感器是通过浮球侵入液体从而反应出相对于的液位,温度的变化势必影响传感器浮球侵入液体的体积,从而影响传感器测量的准确性,特别对于温差较大的系统,其误差有可能超过系统的要求。因此在温度变化较大的系统必须消除温度对磁致伸缩液位传感器的影响。

设温度变化前,滑油密度为ρ,浮球排开滑油的体积为V,温度变化后,滑油密度为ρ′,浮球排开滑油的体积为V′,g为重力加速度,Δρ为温度变化前后滑油密度的变化量,ΔV为温度变化前后浮球排开滑油体积的变化量。根据阿基米德原理得知:

ρgV=ρ′gV′

(3)

因为ρ′=ρ+Δρ、V′=V+ΔV所以可得:

ρV=(ρ+Δρ)(V+ΔV)

(4)

由于ΔρΔV很小,可忽略不计,得:

ρΔV+VΔρ≈0

(5)

所以可得:

Δρ/ρ=-ΔV/V

(6)

由式可知,浮球排开滑油体积的变化量与滑油密度的变化率成正比。以柱状浮球分析,设浮球外圆直径为R,浮球内圆直径为r,浮球排开滑油的体积为V,浮球排开滑油体积的变化量为ΔV,h为浮子高度,由圆柱体体积公式可知:

V=π(R2-r2)h

(7)

ΔV=π(R2-r2)Δh

(8)

由式(7)和式(8)代入式(6)得知,

Δh=h(-Δρ)/ρ

(9)

可见,滑油密度的改变会改变浮球浸入滑油的高度,浸入滑油的高度改变势必使得液位读数发生改变,使得测量产生了误差。

通过上述对温度影响磁致伸缩液位传感器测量精度的分析可知,温度会对多种因素产生影响,因此使用硬件设计不易于对多种影响因素进行修正,可以通过使用结合智能算法的软件修正方式对其补偿。

2 改进型ANFIS

2.1 典型自适应神经模糊推理系统

典型的自适应神经模糊推理系统结构如图2所示,通常分为5层网络,包括两个输入层,两个规则层与一个输出层。系统中带有参数的自适应节点用方形节点表示,不带参数的固定节点由圆形节点表示[14]。

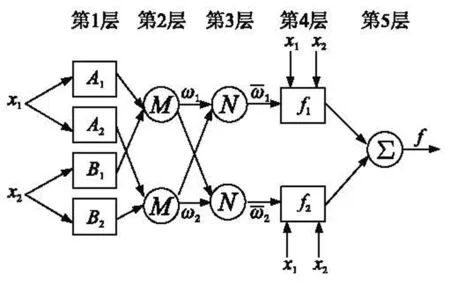
图2 典型ANFIS结构图

第1层将输入的变量进行模糊化,节点输出为:

(10)

(11)

节点的输出即模糊变量Ai、Bj的隶属度函数值,其表示节点输入x1、x2分别隶属于Ai、Bj的程度。本文应用的隶属度函数使用高斯型函数:

(12)

(13)

式中:ci,1、cj,1为隶属度函数中心,属于前题参数;σi,1、σj,1为隶属度函数的宽度,属于前题参数。

第2层将输入的变量相乘,得到的每个节点的输出即表示一条规则的强度:

(14)

第3层为规则强度的归一化:

(15)

第4层计算每一条模糊规则的输出,此层中的节点为自适应节点,输出为:

(16)

式中:pi,qi,ri为结论参数。

第5层为计算所有输入信号的总输出,其为固定节点,表示为:

(17)

通过对ANFIS结构分析可知,当系统前题参数给定时,自适应神经模糊推理系统网络的输出可由结论参数线性组合得出[15]:

(18)

使用混合学习算法来不断修正前题参数和结论参数即为自适应神经模糊推理系统的核心思想。使用时须要先将一初始值赋给前题参数,并通过使用递推最小二乘估计算法得到结论参数,然后使用梯度下降法将系统误差反向向前传播,即从第5层向第1层传播,从而修正前题参数[16]。

2.2 改进型自适应神经模糊推理系统

由于梯度下降算法具有容易陷入局部极小,训练速度较慢等缺点,因此对ANFIS进行改进,采用附加动量算法来不断修正ANFIS的前题参数,这样就可以将在误差曲面中,由目标误差变化产生的影响和在梯度中目标误差的作用同时进行考虑,它的作用类似于低通滤波器,使得自适应神经模糊推理系统对微弱的、可忽略的变化进行过滤,即使系统具有跳过误差曲线局部极小值的能力[15]。附加动量算法可由公式表示为:

ci(n+1)=ci(n)+Δci(n)

(19)

(20)

σi(n+1)=σi(n)+Δσi(n)

(21)

(22)

式中:n为迭代运算的步数;β(n)为第n步运算的学习率;λ为动量因子,通常取0.95。

使用附加动量法进行修正的实质就是通过一个动量因子来传递最后一次前题参数变化的影响。当该动量因子λ=0时,为传统的ANFIS算法,即前题参数仅受梯度下降法影响;当该动量因子λ=1时,将新的前题参数变化设置为最后一次前题参数的变化,忽略倒由梯度下降法参数的变化部分。这样通过增加动量项,使得前题参数的调节趋向误差曲面底部平均方向变化,当进入误差曲面底部平坦区域时,Δci(n+1)≈Δci(n),从而有效防止出现Δci=0,这样有利于网络从误差曲面的局部极小值中跳出。

由附加动量法设计准则可知,当出现修正的前题参数导致误差产生较大增长,以及当新的误差变化率相对于原值超过了已经设定的最大误差变化率时,则不能采用新的前题参数,避免网络进入较大的误差曲面。因此,为了准确使用修正方法,要在训练程序中加入条件判断条件:

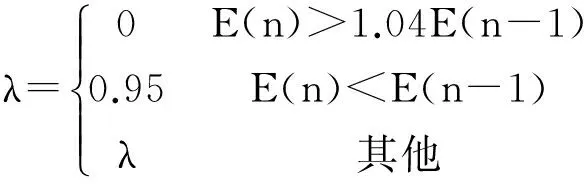
(23)

式中E(k)为第n步误差平方和。

图3 标定测量装置组成

3 温度补偿实验研究

3.1 温度补偿前实验分析

本文研究的液位标定温度补偿试验所使用的标定测试装置组成如图3所示。所研究的传感器为在航空滑油喷嘴流量试验器上用于计量的JLM磁致伸缩液位传感器,其量程范围为0到700mm,非线性度为0.1%,被测液体为HP-8A型航空滑油,滑油的温度范围为20 ℃～70 ℃,温度传感器为WBJ/RPB23ZNd型温度变送器,温度测量量程为0～150 ℃,数据采集系统为西门子S7-300的模拟量采集模块SM331,其具有15位的分辨率。被测试的传感器安装在油桶中,被加热至适当温度的滑油通过滑油喷嘴喷出,进入油桶,油桶与标有刻度的游标连通,油桶中滑油的实际液位通过游标读出,磁致伸缩液位传感器和温度传感器的测量值通过数据采集系统采集处理传至上位机。由于该种滑油主要工作温度为(60±5)℃,所以仅对20 ℃～70 ℃范围内,温度对传感器精度的影响进行研究和修正。

通过实验测得未对传感器进行温度补偿的数据如表1所示。

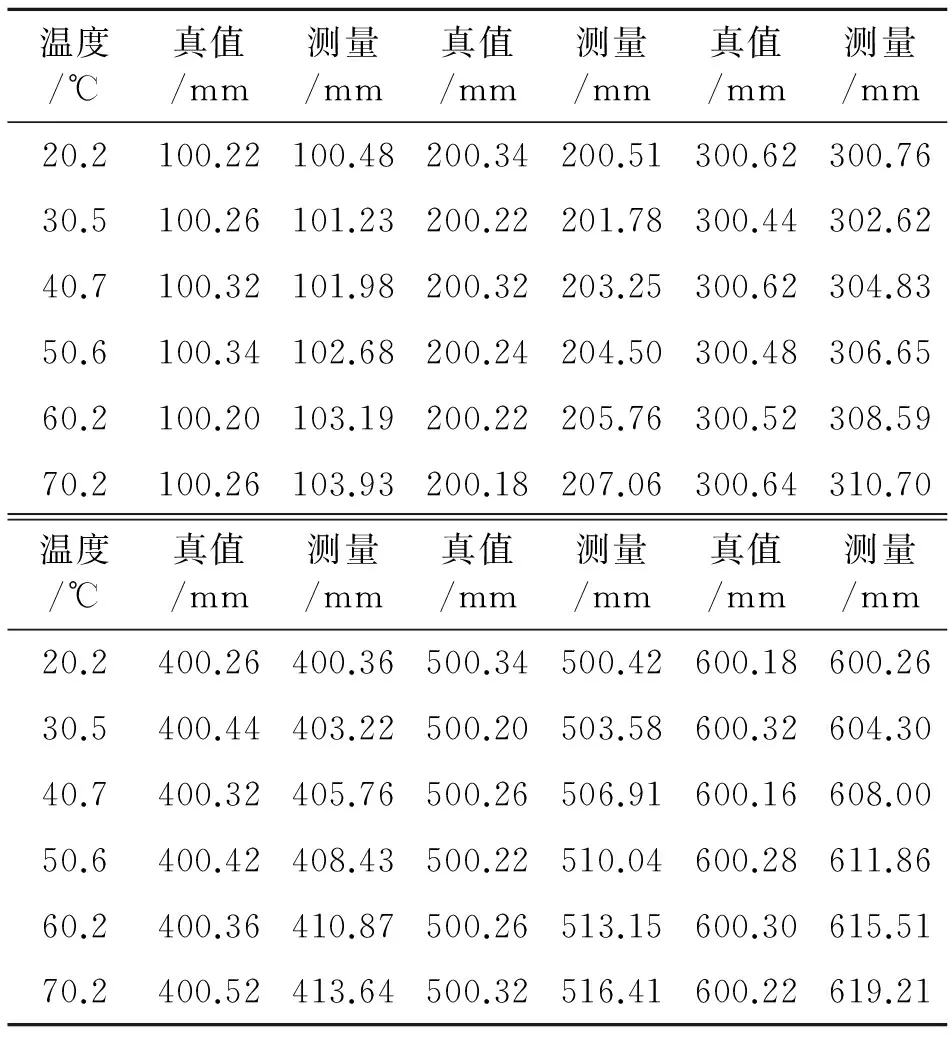
表1 温度补偿前实验数据

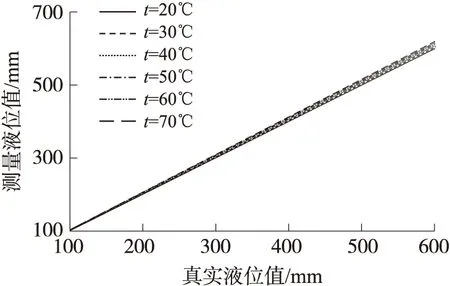
图4 温度补偿前的传感器工作曲线

通过对温度补偿前实验数据进行分析可以看出,在相同实际液位高度下,不同温度测量时间的测量液位值会随着温度升高而增大。通过实验数据得到了传感器进行温度补偿前的传感器工作曲线如图4所示,可以看出在同一温度下,实际液位越高,温度漂移现象越明显,说明液位值越高受到温度的影响越大。在低液位区域,传感器输出的线性度比高液位区域略好。温度补偿前的测量误差曲线如图5所示,在相同温度下,液位值越高,测量时受到温度影响越大,测量误差越大。在70.2 ℃时,传感器在600mm液位测量时会因为温度影响而产生18.5%左右的误差。

图5 温度补偿前的测量误差曲线

3.2 温度补偿后实验分析

温度补偿原理如图6所示。实际液位高度Hr与实际温度Tr共同决定了磁致伸缩液位传感器输出的液位高度Ho,即传感器输出是关于Hr和Tr的函数:Ho=f(Hr,Tr)。为了消除温度Tr对传感器的影响,将温度输出To与实际液位高度Hr作为ANFIS的输入,将用于作为训练样本的实验数据对温度补偿的ANFIS进行训练,通过训练学习,系统能够将输入的实际液位高度Hr、温度To、传感器输出高度Ho建立非线性映射,通过对参数不断优化使得系统输出Hc最终逼近实际液位高度Hr,最后通过测试数据对ANFIS输出的液位高度进行测试。

图6 温度补偿原理

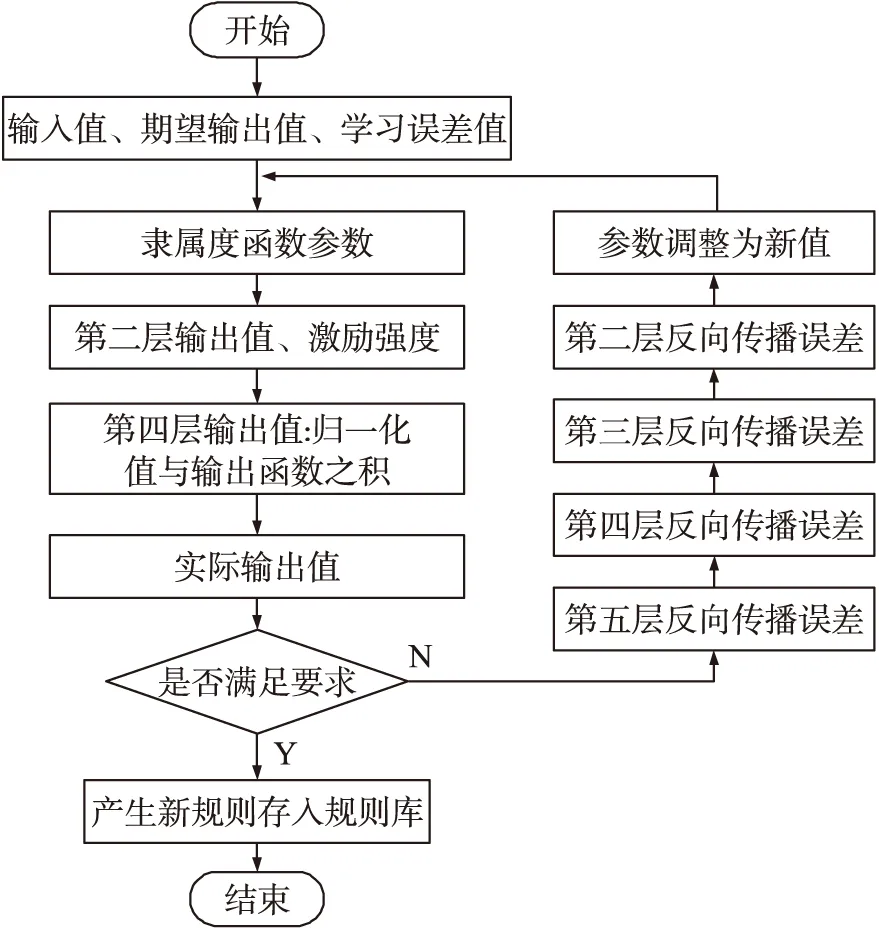
图7 ANFIS程序框图

使用ANFIS进行温度补偿的程序框图如图7所示。使用温度范围在20 ℃～70 ℃,液位范围在100mm～600mm的未经过温度补偿的实验数据作为ANFIS的训练样本,为了消除量纲不同对计算的产生的影响对采集的数据进行归一化处理[17]:

(24)

隶属函数选取为三角函数,设定a、b、c参数的学习率为0.01;允许误差为1×10-4。隶属函数个数将决定ANFIS训练结果的质量,因此需要选取合适的隶属函数个数。通过仿真研究可知,增大隶属函数个数可以减小误差,但会增加计算量,经过比较隶属函数个数选为7时的训练效果相对较好[18]。

使用梯度下降算法作为误差反向传播算法时,设置目标误差为1×10-4,通过301步迭代运算可以达到误差要求,而使用动量附加算法作为误差反向传播算法时,设置目标误差为1×10-4,通过174步迭代运算可以达到误差要求,通过补偿后的实验数据如表2所示。

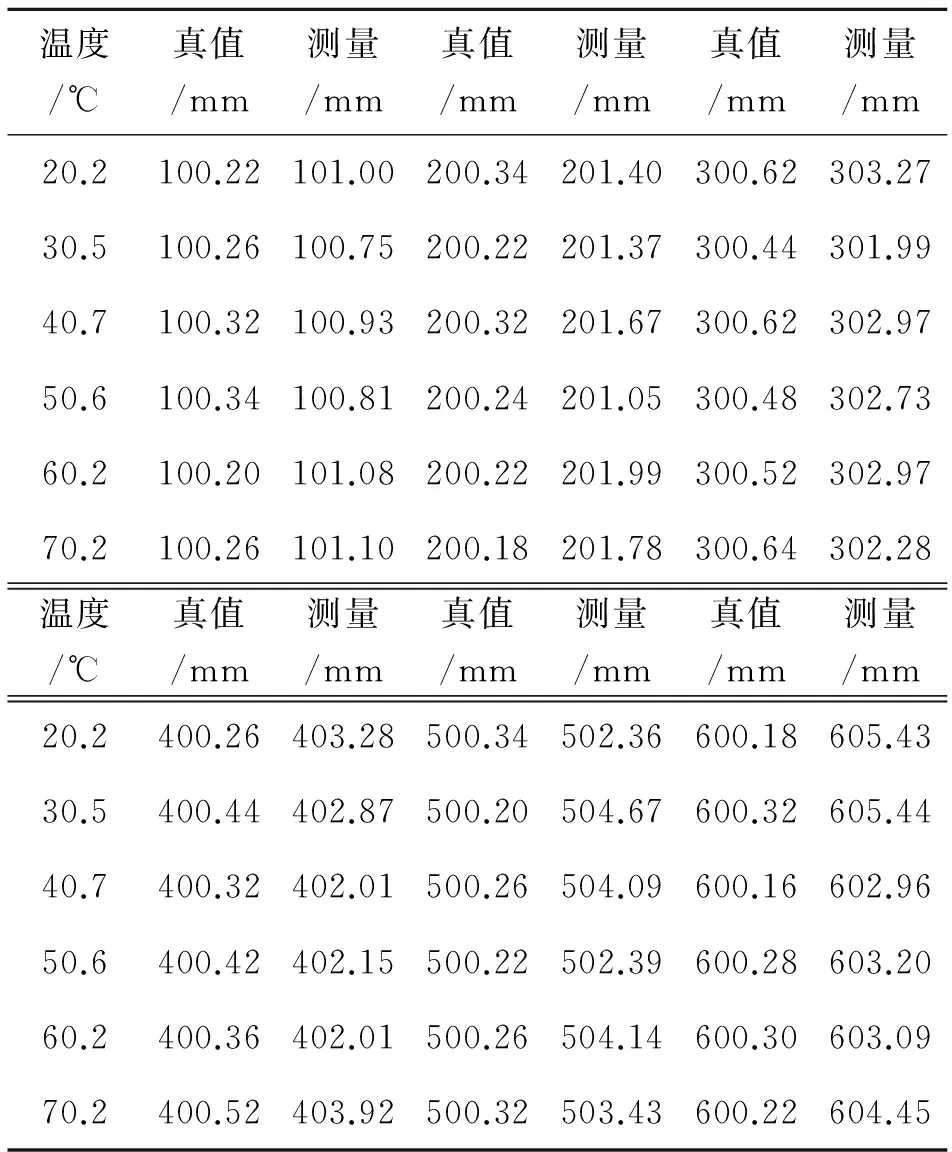
表2 温度补偿后实验数据

通过温度补偿后的实验数据得到传感器的工作曲线如图8。补偿后传感器的输出基本不会受到温度影响,线性度非常好。温度补偿后的测量误差曲线如图9所示,可以看出通过使用改进型ANFIS温度补偿后,在20 ℃～70 ℃温度范围内,100 mm～600 mm液位范围内的测量误差均低于0.88%。

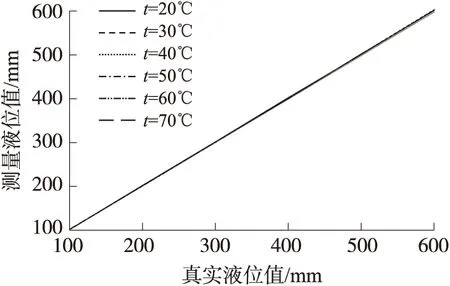
图8 温度补偿后的传感器工作曲线

图9 温度补偿后的测量误差曲线

为比较改进型ANFIS温度补偿系统的优势,建立基于PSO-LSSVM模型和基于BP神经网络的温度补偿模型,并利用同样的数据样本对网络进行训练。对PSO-LSSVM模型设置进化代数为100,种群规模为40,c1=c2=2.5;对BP神经网络模型选择隐含层的单元数为11,选择Sigmoid函数为隐含层函数,Pureline线性函数为输出层计算函数,trainlm为训练函数,设置最大训练次数为1500[19]。得到3种温度补偿模型的效果对比如表3所示。

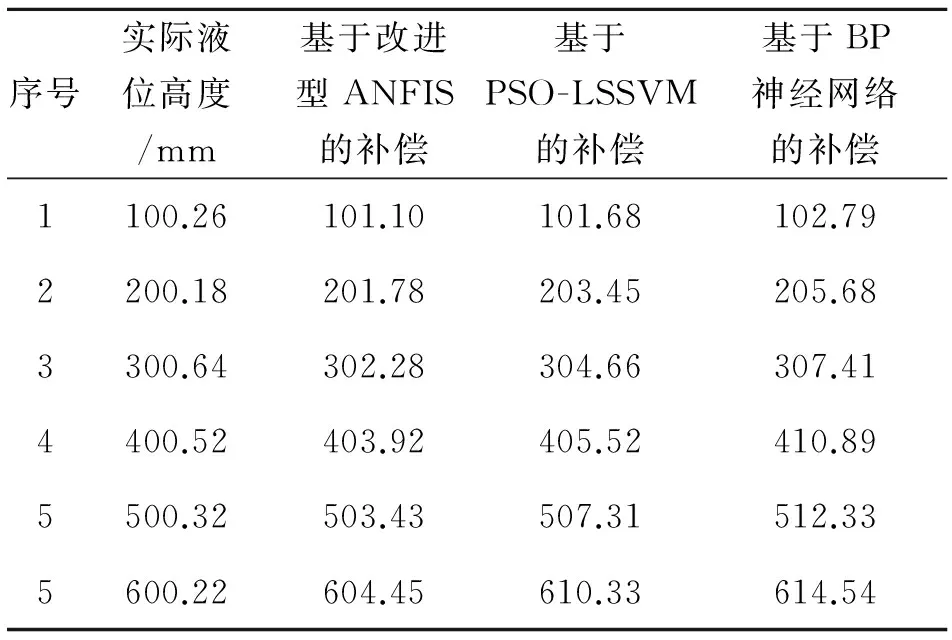
表3 温度补偿效果对比

使用相对误差作为衡量温度补偿效果的标准:

er=(Hc-Hr)×100%/Hr

(25)

式中:Hc为补偿后液位测量值;Hr液位实际高度。

通过将表3中的温度补偿实验数据与表1的未补偿的实验数据相比较,可以看出3种补偿方法均可以在一定程度上有效补偿温度对传感器产生的影响。对比表3中3种不同补偿方法的效果,可以看出使用了基于BP神经网络的补偿方法的相对误差最大为3.65%,平均为3.12%,使用了PSO-LSSVM补偿方法的相对误差最大为2.18%,平均为1.92%,而改进型ANFIS方法的相对误差最大为0.88%,平均为0.65%,远小于另外两种补偿方法[20]。这说明使用了改进型ANFIS的温度补偿方法能够有效消除温度对磁致伸缩液位传感器的影响。

4 结论

①介绍了磁致伸缩液位传感器的工作原理,对由于被测液体温度变化而产生的误差机理进行了分析。

②针对传感器的温度补偿,对自适应神经模糊推理系统进行改进,采用附加动量算法不断修正自适应神经模糊推理系统中的前题参数以避免采用梯度下降算法时易陷入局部极小,训练速度较慢等缺点,提高系统的忽略网络中微小变化的能力。

③将改进型ANFIS温度补偿方法进行实际测试,并于基于BP神经网络和基于PSO-LSSVM模型的温度补偿方法进行比较,改进型ANFIS温度补偿性能优于BP神经网络和基于PSO-LSSVM模型的温度补偿方法,具有很强的泛化能力。

[1]李春楠,卢云,兰中文,等.磁致伸缩位移传感器的研究进展[J].实验科学与技术,2008,1(6):10-12

[2]冯建,赵辉,刘伟文,等.陶若杰磁致伸缩位移传感器电路系统的设计[J].电子测量技术,2010,1(33):11-13

[3]Fernando Seco,José Miguel Martín,Antonio Ramón Jiménez.Improving the Accuracy of Magnetostrictive Linear Position Sensors[J].IEEE Transactions on Instrumentation and Measurement,2009,3(58):722-728

[4]李怀洲,李庆山,孙振伟,等.磁致伸缩位移传感器信号处理电路的研究与实现[J].仪器仪表学报,2004,25(S4):138-141

[5]Liu Huifang,Jia Zhenyuan,Wang Fuji,et al.Study on the Design Method of Giant Magnetostrictive[C]//Beijing,China,Proceedings of the IEEE International Conference on Mechatronicsand Automation,2011:1098-1103

[6]Woochul Kim,Yoon Young Kim.Design of a Bias Magnetic System of a Magnetostrictive Sensor for Flexural Wave Measurement[J].IEEE Transactions on Magnetics,2004,5(40):3331-3338

[7]颜庆伟,赵玉龙,蒋庄德.磁致伸缩液位传感器的电路设计及性能分析[J].传感技术学报,2008,21(5):777-780

[8]代前国,周新志.大位移磁致伸缩传感器的弹性波建模与分析[J].传感技术学报,2013,26(2):195-199

[9]王峥,常晓明,脇若弘之.长线磁致伸缩位移传感器的磁极化强度模型[J].传感技术学报,2010,23(8):1075-1078

[10]陶若杰,赵辉,刘伟文,等.双丝差动型磁致伸缩位移传感器结构设计[J].传感技术学报,2010,23(6):799-802

[11]李永波,胡旭东,曾宗云.温度对磁致伸缩液位传感器测量精度的影响[J].工业仪表与自动化装置,2007(6):11-13

[12]Weng Ling,Wang Bowen,Sun Ying,et al.Model and Experiment of Giant Magnetostrictive Vibration Sensor[C]//China,11th International Conference on Electrical Machines and Systems,Wuhan,2008:4092-4095

[13]Affanni A,Guerra A,Dallagiovdnna L,et al.Design and Characterization of Magnetostrictive Linear Displacement Sensors[C]//CoMo,Ital,Proceedings of the 21st IEEE Instrumentation and Measurement Technology Conference,2004:206-209

[14]张浩炯,余岳峰,王强.应用自适应神经模糊推理系统(ANFIS)进行建模与仿真[J].计算机仿真,2002,19(4):47-49

[15]王艳永,邓方,孙健.改进型自适应神经模糊推理系统的角度传感器误差补偿方法[J].控制理论与应用,2013,30(10):1342-1346

[16]刘应吉,张天侠,闻邦椿,等.基于自适应模糊推理系统的柴油机故障诊断[J].系统仿真学报,2008,20(21):5836-5839

[17]孙艳梅,都文和,冯昌浩,等.基于蚁群聚类算法的RBF神经网络在压力传感器中的应用[J].传感技术学报,2013,26(6):806-809

[18]徐相波,陈金辉,刘景峰.基于自适应神经模糊推理系统的低压配电无功补偿方法[J].低压电器,2012(3):29-31

[19]张朝龙,江巨浪,李彦梅,等.基于云粒子群-最小二乘支持向量机的传感器温度补偿[J].传感技术学报,2012,25(4):472-477

[20]孙艳梅,刘树东,苗凤娟,等.基于遗传算法的小波神经网络温度补偿模型[J].传感技术学报,2012,25(1):77-81.

Research on Temperature Compensation System of Magnetostrictive Liquid Level Sensor Based on Improved ANFIS*

XIEMiao*,LIUZhixiang,MAOJun

(School of Mechanical Engineering,Liaoning Technical University,Fuxin Liaoning 123000,China)

Taking into account the temperature drift of the magnetostrictive liquid level sensor is serious in the large temperature difference,and it is difficult to use the mathematical model to express the nonlinear relation between temperature drift phenomenon and the variety of factors,establish a temperature compensation system based on improved ANFIS.This system uses the Additional momentum method to constantly modify premise parameters in ANFIS in order to avoid the shortcomings that it easy to fall into local minimum point and slow training speed when using the gradient descent algorithm,and improve the capacity of ignoring tiny changes in the network.In order to verify the performance of the temperature compensation system,it has been compared with other temperature compensation system based on PSO-LSSVM and BP neural network.Analysis and experimental results show that the maximum error and its mean error of improved ANFIS model is 0.88% and 0.65%,far less than the other two kinds of compensation methods.This temperature compensation system based on improved ANFIS has strong generalization ability and can effectively eliminate the influence by temperature on the magnetostrictive liquid level sensor.

magnetostrictive liquid level sensor;temperature compensation;improved ANFIS;BP algorithm;Neural network;PSO-LSSVM model

谢 苗(1980-),女,辽宁大连人,副教授,博士生导师,主要研究方向为机械动力学分析及控制的研究,xiemiao1121@126.com;

刘治翔(1988-),男,辽宁大连人,博士研究生,主要研究方向为智能控制,传感器信号与信息处理,380357369@qq.com;

毛 君(1960-),男,教授,博士生导师,主要从事机械动态设计及仿真、机电一体化研发方面的科研与教学工作。

项目来源:国家自然科学基金项目(51304107);辽宁省煤矿液压技术与装备工程研究中心开放基金项目(CMHT-201206);辽宁省教育厅项目(L2012118)

2014-07-20 修改日期:2014-11-11

C:7230

10.3969/j.issn.1004-1699.2015.01.010

TP212.9

A

1004-1699(2015)01-0049-07