基于近完全时滞补偿的隐式实时混合试验方法

王 贞， 刘进进， 吴 斌， 许国山

(1.哈尔滨工业大学结构工程灾变与控制教育部重点实验室， 黑龙江 哈尔滨 150090; 2.哈尔滨工业大学土木工程学院， 黑龙江 哈尔滨 150090; 3.苏州设计研究院股份有限公司， 江苏 苏州 215021)

基于近完全时滞补偿的隐式实时混合试验方法

王 贞1,2， 刘进进3， 吴 斌1,2， 许国山1,2

(1.哈尔滨工业大学结构工程灾变与控制教育部重点实验室， 黑龙江 哈尔滨 150090; 2.哈尔滨工业大学土木工程学院， 黑龙江 哈尔滨 150090; 3.苏州设计研究院股份有限公司， 江苏 苏州 215021)

实时混合试验是一种新型结构抗震混合试验方法。隐式逐步积分算法虽然具有稳定性好的特点，但在实时混合试验中实施困难。在分析两种多自由度隐式实时混合试验方法的基础上，结合近完全时滞补偿方法，提出了一种新型隐式实时混合试验方法，并分析了该方法的性能。数值模拟表明，该方法具有较高的收敛速度和计算精度，能够同时考虑时滞补偿，能满足自由度数目较多的多自由度结构实时混合试验的要求。

实时混合试验； 隐式逐步积分算法； 时滞补偿； 迭代

引 言

传统的抗震试验方法有三类，即拟静力、拟动力和振动台。近些年，拟动力试验方法得到了快速发展，出现了子结构化、网络化和实时化的趋势，分别产生了子结构拟动力试验方法、网络分布式拟动力试验和实时混合试验(有时也称实时子结构试验或者动力子结构试验等[1-4])。实时混合试验方法把原型结构分割为试验子结构和数值子结构，分别通过真实试验和实时计算进行模拟，二者之间的相互作用通过液压伺服加载系统的实时加载保证。试验子结构往往是具有很强非线性或者力学性能时间相关的构件或子结构，数值子结构是原型结构的其余部分。实时混合试验由于实时执行加载和数值仿真，能反应试件的速度/加速度相关力学性能，弥补了传统拟动力试验方法的不足，近些年得到了快速发展。为了保证实时加载[5-6]和实时计算[7]，尤其前者，使得实时混合试验具有更大挑战。

实时混合试验需要在线实时求解结构的运动方程，对逐步积分算法提出了较高要求。常用的显式算法，如中心差分法，由于其条件稳定性而可能在保证计算实时性时无法满足对积分步长的限制条件。目前已经提出的基于隐式的实时混合试验方法，主要有两种，即吴斌等人提出的等效力控制方法[8-9]和Shing等人提出的实时迭代混合试验方法[10]。此两种方法取得了一定的成功，但也存在一定的局限性。本文在分析它们局限性的基础上，结合作者提出的时滞补偿方法[11-12]，提出了一种新的隐式实时混合试验方法，研究表明该方法对于多自由度结构实时混合试验具有较明显的优势。

1 现有隐式实时混合试验方法

实时混合试验离散运动方程和基于常加速度假定的位移、速度表达式为：

MNai+1+CNvi+1+RN(di+1)+RE(ai+1，vi+1，di+1)=

Fi+1

(1)

(2)

(3)

式中 角标N表示数值子结构，角标E表示试验子结构；M为结构质量矩阵；C为结构阻尼矩阵；R为子结构恢复力向量；F为外部荷载向量；d，v，a分别为结构位移、速度、加速度向量；Δt为逐步积分时间间隔。

对式(2)和式(3)进行整理，用di+1和上一步结构响应来表示vi+1和ai+1，并代入结构的运动方程(1)，可得

RN(di+1)+KPDdi+1+RE(ai+1，vi+1，di+1)=FEQ，i+1

(4)

其中

(5)

(6)

式(4)是一个关于di+1的非线性方程，在采用牛顿迭代法求解时，有：

(7)

(8)

(1)迭代收敛速度的波动导致作动器运动不平稳，容易对作动器造成损伤且得不到试件的真实力反应；

(2)不易在线获得结构刚度，矩阵求逆耗时较大。

针对隐式实时混合试验存在的问题，Shing等人[10]提出了以实时迭代、插值发送命令等为特征的方法，如图1所示。主要内容包括：

(9)

(3)考虑到固定迭代次数及作动器时滞等因素带来的误差，在每积分步最后一个迭代步进行修正。取积分步末点处的位移di+1为

(10)

试验子结构的恢复力修正为

(11)

Shing方法取得了一定的成功，但仍然存在如下问题：1)通过对迭代位移进行插值发送命令，虽然解决了作动器加载速度突变的问题，但改变了下一次迭代计算的起点，不仅使得迭代过程变得复杂，收敛速度也大幅下降，最后一迭代步可能仍然存在较大误差。2)在积分步长内每个采样时刻点迭代一次，意味着必须在一个控制采样步长内完成迭代计算、位移命令的内插并发送给作动器，当结构自由度较多时，很可能无法满足实时性的要求。3)即使迭代获得精度很高的位移，位移命令进行加载时不可避免地涉及系统时滞的影响，引入新的误差。

图1 位移命令插值示意图[10]Fig.1 Schematic for displacement command interpolation[10]

等效力控制方法[8-9]把式(4)等号左侧看作是3个并联元件，采用力反馈控制环取代了数值迭代来求解该方程，其原理如图2所示。图中CF称为力-位移转化矩阵，功能是把力信号转化成位移信号，实现作动器的位移控制加载。采用该方法执行实时混合试验的流程是，首先得到第i+1步的等效力，内插得到积分步内的等效力命令，并在对应的时刻发送给控制回路，作动器受相应的位移命令驱动；在积分步长结束时，把试件的反力反馈到式(4)，再次求解位移，以降低控制误差造成的影响。

可见，等效力控制方法创造性地提出采用控制的思路求解非线性方程，由于引入了控制的思想，使其具有鲜明的个性和突出的特点。分析表明，采用积分控制器并且阶跃发送命令的等效力控制方法类似于传统的迭代方法。合理设计的控制器可以较好地考虑等效力命令插值带来的影响，而数值迭代则很难实现这一点。此外，由于采用了力反馈控制环，等效力控制方法可以同时考虑到系统作动性能和迭代过程，在一定程度上减小了系统时滞。不过，该方法存在以下缺点：1)内插发送等效力命令，虽然能保证作动器运动的连续性，但会导致系统的控制性能变差。2)虽然合理设计的等效力控制器可以有效减小系统时滞，但是有时仍需要其他时滞补偿方法来补偿系统时滞。3)积分步内固定计算次数，要求数值子结构静反力和等效力偏差的求解等过程必须在一个控制采样步长内完成，尤其是最后一个计算步内，还要完成位移的修正计算。当数值子结构自由度较多时，矩阵运算复杂耗时，很难满足实时混合试验实时性的要求。

2 基于近完全时滞补偿方法的隐式实时混合试验方法

纵观前述两种隐式实时混合试验方法，它们的主要缺点是：1)计算耗时：每一计算步复杂耗时的矩阵计算必须在一个控制采样步长内完成，限制了数值子结构的复杂程度；2)计算精度：每一采样步的计算以当前所实现的位移为基础，计算收敛速度有很大程度的下降，在固定次数计算后可能仍然存在较大误差，该误差在试验过程中传播、累积，对试验结果可能产生较大影响；3)系统时滞：即使一个积分步长内的计算精度很高，将位移命令发送给作动器进行加载时，不可避免地涉及到时滞，因此会受到时滞补偿效果的影响。

鉴于此，提出以近完全时滞补偿方法为基础的隐式实时混合试验方法。近完全时滞补偿方法[11,12]的主要特点是借助过预测结构位移响应，使得试验子结构的位移超前于数值子结构，只需在已实现的实测位移数据中搜索与期望位移最接近的位移值，同一时刻测得的试件子结构反力即为试验子结构与期望位移对应的反力。

在进行隐式实时混合试验非线性方程的迭代求解时，若采用近完全时滞补偿方法进行时滞补偿，由于试验子结构的位移响应超前于数值子结构，迭代计算得到位移后，无需发送给作动器进行加载，而是直接从当前完成的实测位移数据中搜索得到与迭代位移近似相等的试验子结构位移值，同一时刻的试验子结构实测反力即为与当前迭代位移相对应的反力值，将其直接带入下一迭代步进行计算即可。图3是基于近完全时滞补偿方法[11-12]的隐式实时混合试验方法原理示意图。下面以试验子结构为弹簧试件的单自由度结构体系为基础，对照图3详细介绍基于近完全时滞补偿方法的隐式实时混合试验方法的流程(后文统一称之为“新方法”)：

图2 基于等效力控制方法的实时混合试验原理Fig.2 Principle of real-time hybrid testing based on equivalent force control method

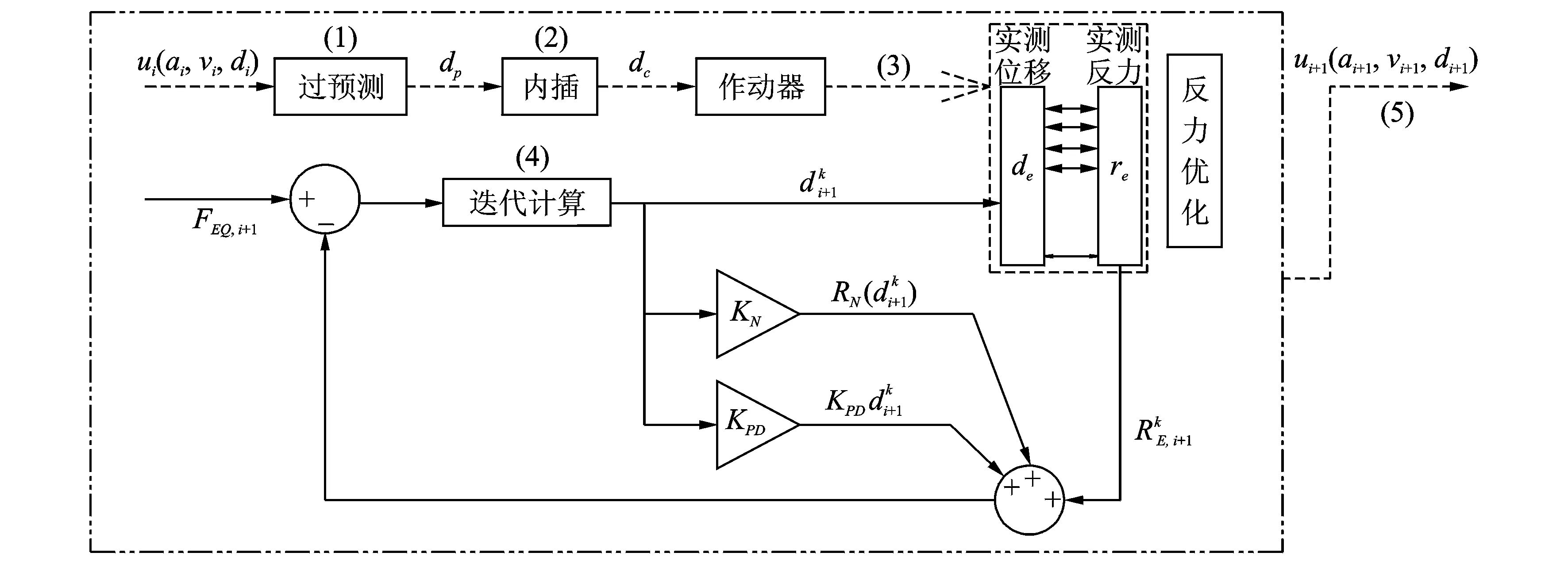
图3 基于近完全时滞补偿方法的隐式实时混合试验原理Fig.3 Principle of implicit real-time hybrid testing based on nearly-complete delay compensation method

1)位移过预测：ti时刻预测ti+1+τp时刻的位移，如采用显式Newmark表达式，有dti+1+τp=di+vi(τp+Δt) +0.5ai(τp+Δt)2，τp=τa+Δτ，τa为预估的作动器最大时滞，Δτ为过预测时间跨度；

2)内插生成作动器位移命令：在dti+1+τp与ti时刻的作动器位移命令dti+τp之间，内插得到作动器位移命令dc(ti～ti+1)，并发送给作动器。

3)采集数据：采集试验子结构位移响应de(ti～ti+1)及试件反力RE(ti～ti+1)。

4)迭代求解非线性方程：

①每积分步第一次迭代以上一步的位移响应为初值，其余次迭代以上次迭代结果为初值;

④进行多次迭代，直到收敛；更新位移预测所需的位移di+1、速度vi+1、加速度ai+1；当试验时间达到ti+1，开始下一个积分步的计算。

可见，基于近完全时滞补偿方法的隐式实时混合试验方法具有如下特点：1)采用简化牛顿迭代，仅需试验前计算逆矩阵；2)第k+1迭代步的计算完全基于第k迭代步的位移及其响应进行，实现了标准的简化牛顿迭代，其迭代收敛速度要优于Shing方法和等效力控制方法，计算效率更高；3)积分步长内无固定迭代次数，位移迭代达到收敛精度即可，而收敛迭代次数预期少于前两种方法；4)在积分步长内作动器的加载不依赖于当前迭代位移值，只要在一个积分步长内完成迭代收敛计算即可，对单步计算时间的限制比前两种方法宽松，能适应自由度数目更多的结构；5)作动器的加载基于预测位移内插生成位移命令进行，不会出现加载速度失真现象，并能保证试件加载的实时性；6)在迭代求解非线性方程的同时已经考虑了作动器加载过程中的时滞，并进行了时滞补偿；7)该方法的不足是，采取了位移过预测方法，预测的时间跨度更大，带来了更大的预测误差。该误差可以通过预测精度更好的位移预测方法并通过回搜过程来减小。此外，还可通过其他方法先降低系统时滞，以减少预测跨度过大带来的预测误差。

3 数值模拟

3.1 单积分步计算精度

数值分析表明，对于不考虑时滞的小步长分析，三种方法都具有较好的精度。考虑到多自由度分析中存在高频成分、实时计算要求采用较大步长，采取如下参数：采样步长δt=0.004 s，积分步长Δt=0.04 s;采用积分等效力控制器，控制参数KI=400；结构参数为：KE=2×103N/m，MN=1 kg，KN=2×103N/m。三种方法单积分步位移计算结果如图4所示。可见，在积分步长较大或结构频率较高时，即使在最后一个计算步对积分点位移进行了修正，Shing方法和EFCM方法的收敛精度也不是很理想。

图4 单积分步计算精度比较Fig.4 Computational accuracy comparisons in single integration step

时滞补偿是实时混合试验最关键的问题，鉴于时滞可能发生波动，采用常规补偿方法很难实现实测的完全补偿，接下来的分析中假定存在约1 ms的欠补偿时滞。作动器模型取为一阶传递函数TA(s)=700/(700+s)，对于频率为1 Hz的信号，该系统时滞约为1 ms。取积分步长Δt=0.01 s，不同方法的单积分步计算精度如图5所示。可见，时滞得不到完全补偿时，Shing方法和EFCM的单积分步计算精度低于新方法。

由前述分析可知，数值子结构自由度较多或结构频率较高时，Shing方法和EFCM的计算精度会有所下降；实际试验的欠补偿时滞也会使得两种方法计算精度下降。即使进行了位移修正，计算精度也不如所提出的基于简化牛顿迭代的新方法。

图5 时滞欠补偿时单积分步位移计算精度比较Fig.5 Computational accuracy comparisons in single integration step with under-compensated delay

3.2 计算耗时

本小节比较应用于多自由度结构实时混合试验时Shing方法、EFCM和新方法的计算耗时情况。取如图6所示的5层剪切型结构为分析对象，层间刚度为ki=40×103N/m，集中质量为mi=100 kg(i=1～5)，结构自振频率为0.91，2.64，4.17，5.36，6.11 Hz，结构无阻尼。选底层柱为试验子结构，刚度取kE=k1/2。采用理想作动器模型进行数值模拟，积分步长取Δt=0.01 s，每个积分步计算10次。新方法的计算精度取10-7m。计算平台参数如表1所示。

图6 5自由度结构计算示意图Fig.6 Computational schematic of 5DOF structure

单积分步内的各迭代步耗时如图7所示。可见，3种方法单迭代步的耗时并无太大差别，均约为1×10-5s。3种方法的第一迭代步耗时较其余步更大。EFCM在最后一个迭代步要完成位移命令计算和位移修正计算，计算耗时增加。新方法由于收敛速度较快，只进行3次迭代计算即达到精度要求，完成了该积分步内方程求解。在实时混合试验中，Shing方法和EFCM方法要求采样步长大于单步迭代最大耗时，新方法的迭代次数远小于它们，因此新方法大大提高了计算效率，更适用于多自由度结构实时混合试验。进一步的时程耗时分析见文[13]。需要说明的是，计算耗时统计是在性能较高的计算机上完成，各计算步耗时均较小。实际试验中，控制板不仅要完成数值子结构的计算、时滞补偿计算，还要完成液压伺服作动器的控制计算，多任务的同步实时处理，使得所能完成的实时混合试验的自由度数目大大受限。

图7 单积分步计算耗时Fig.7 Time consumed for computation in single integration step

表1 计算平台参数

3.3 时程分析

为了进一步检验3种方法的性能，分别完成了无阻尼自由振动、无阻尼地震激励、非线性自由振动、非线性地震激励等多种工况的数值模型。限于篇幅，此处仅介绍最后一种工况的数值模拟。

分析模型为图6所示的5层剪切型结构，假设试验子结构具有双线性恢复力关系，起始刚度为kE= 20×103N/m，屈服位移为0.008 m，屈服后刚度为起始刚度的0.115倍。首层自由度初始位移为0，初始速度为0；其他自由度的初始状态为0。外荷载激励取El Centro(NS，1940)地震记录，峰值加速度调为0.2g。

考虑未能完全补偿时滞的影响，即假设欠补偿时滞约为1 ms，取作动器模型为TA(s)=700/(700+s)。等效力控制器参数不变。首层自由度位移时程及恢复力-位移关系见图8和9所示。可见新方法的计算精度要好于其他两种方法。

图8 位移时程Fig.8 Displacement time histories

图9 试件恢复力-位移曲线Fig.9 Restoring force-displacement relation of specimen

4 结 论

分析了Shing方法和等效力控制方法(EFCM)在实时混合试验中可能存在的困难，提出了基于近完全时滞补偿方法的隐式实时混合试验方法，详细阐述了其原理和实现流程，并从理论上分析了其特点。最后，通过数值模拟比较了三种方法在收敛速度和计算精度等方面的性能，验证了理论分析结果。主要结论如下：

1)Shing方法和EFCM应用于多自由度结构实时混合试验时，可能会由于自由度数目的增多，使得运算耗时增加，难以满足实时性的要求；

2)当积分步长增大或试验子结构的初始刚度较大，以及试验中可能存在时滞欠补偿情况时，Shing方法和EFCM的计算精度会有所下降；

3)基于近完全时滞补偿方法的隐式实时混合试验方法，具有较高的计算精度和收敛速度，能够同时考虑时滞补偿，能满足较多自由度数目的多自由度结构实时混合试验的要求。

[1] Nakashima M, Kato H, Takaoka E. Development of real-time pseudo-dynamic testing[J]. Earthquake Engineering & Structure Dynamics, 1992,21(1):79—92.

[2] 吴斌,王倩颖.实时子结构实验的研究进展[J].实验力学,2007,22(5):1—9.

Wu Bin, Wang Qianying. Development of real-time substructure testing[J]. Journal of Experimental Mechanics, 2007,22(5):1—9.

[3] 迟福东,王进廷,金峰,等.土-结构动力相互作用的实时耦联动力试验的时滞稳定性[J].工程力学,2012,29(8):1—7.

Chi Fudong, Wang Jinting, Jin Feng, et al. Delay-dependent stability of real-time dynamic hybrid testing for soil-structure interaction analysis[J]. Engineering Mechanics, 2012,29(8):1—7.

[4] 蔡新江,田石柱.振动台试验方法的研究进展[J].结构工程师,2011,27(增刊):42—46.

Cai Xinjiang, Tian Shizhu. Research advances of shaking tabel testing method[J]. Structural Engineers, 2011,27(Sup):42—46.

[5] Horiuchi T, Inoue M, Konno T， et al. Namita. real-time hybrid experimental system with actuator delay compensation and its application to a piping system with energy absorber[J]. Earthquake Engineering & Structural Dynamics, 1999,28(10):1 121—1 141.

[6] 王贞,吴斌.基于最小二乘法的时滞实时在线估计方法[J].振动工程学报,2009,22(6):625—631.

Wang Zhen, Wu Bin. A real-time approach to delay estimation based on the Least-Square algorithm[J]. Journal of Vibration Engineering, 2009,22(6):625—631.

[7] 贾传果,李英民,刘立平，等.Rosenbrock耦合积分方法及其收敛性分析[J].重庆大学学报,2013,36(2):127—133.

Jia Chuanguo, Li Yingmin, Liu Liping, et al. Rosenbrock-based coupled time integration method and its convergence analysis[J]. Journal of Chongqiong University, 2013,36(2):127—133.

[8] Wu B, Wang Q, Shing P B, et al. Equivalent force control method for generalized real-time substructure testing with implicit integration[J]. Earthquake Engineering & Structural Dynamics, 2007,36:1 127—1 149.

[9] 许国山,吴斌.采用等效力控制方法的非线性结构实时子结构试验[J].振动工程学报,2010,23(3):237—242.

Xu Guoshan, Wu Bin. Real-time substructure testing of nonlinear structures with equivalent force control method[J]. Journal of Vibration Engineering, 2010,23(3):237—242.

[10]Jung R, Shing P, Stauffer E, et al. Performance of a real-time pseudo-dynamic test system considering nonlinear structural response[J]. Earthquake Engineering & Structural Dynamics, 2007,36(12):1 785—1 809.

[11]Bin Wu, Zhen Wang, Oreste S. Bursi. Actuator Dynamics Compensation Based on Upper Bound Delay for Real-time Hybrid Simulation[J]. Earthquake Engineering & Structural Dynamics, 2013,42(12):1 749—1 765.

[12]王贞,刘进进,吴斌.实时混合试验近完全时滞补偿方法的参数确定[J]. 工程力学，2014,31(10):158—166.

Wang Zhen, Liu Jinjin, Wu Bin. Parameter determination of Nearly-complete compensation scheme for time delay in real-time hybrid simulation[J]. Engineering Mechanics, 2014,31(10):158—166.

[13]刘进进.近完全时滞补偿方法及其在实时混合试验中的应用[D].哈尔滨：哈尔滨工业大学, 2013.

Liu Jinjin. Nearly complete compensation scheme for time delay and its application to real-time hybrid testing[D]. Harbin: Harbin Institute of Technology, 2013.

Implicit method for real-time hybrid testing based on nearly-complete delay compensation scheme

WANGZhen1,2,LIUJin-jin3,WUBin1,2,XUGuo-shan1,2

(1.Key Lab of Structures Dynamic Behavior & Control (Harbin Institute of Technology), Ministry of Education,Harbin 150090, China; 2.School of Civil Engineering, Harbin Institute of Technology, Harbin 150090, China;3.Suzhou Institute of Architectural Design Co., LTD., Suzhou 215021, China)

Real-time Hybrid Testing (RHT) is a novel hybrid testing method for evaluating structural seismic performance. Even though implicit time-stepping approaches exhibit better stability, their applications to RHT are limited due to their difficulties. This paper firstly analyses limitations of two existing implicit RHT schemes for Multi-Degree of Freedom (MDoF) structures, and then proposes a new implicit RHT based on the nearly-complete delay compensation developed by the authors formerly. Theoretical performance analysis and numerical simulations are performed following that. Numerical simulations show that the proposed scheme is endowed with better convergence speed and accuracy and incorporates delay compensation, which indicate that it is more suitable to RHT for MDoF systems.

real-time hybrid testing; implicit time-stepping method; delay compensation; iteration

2013-12-01；

2014-07-14

国家自然科学基金国际合作项目(51161120360)和重点项目(91315301-09);中国博士后科学基金面上资助项目(2013M531046);中央高校基本科研业务费专项资金资助项目(HIT.NSRIF.2014102);哈尔滨工业大学海外博士科研启动项目

TU317； P315.9

A

1004-4523(2015)03-0418-07

10.16385/j.cnki.issn.1004-4523.2015.03.011

王贞(1983—), 男, 博士，讲师。电话： 15004548396； E-mail: zhenwang@hit.edu.cn