汽车防撞雷达系统设计

孙 昱，柳贵东，付少波

(军事交通学院基础部，天津300161)

汽车防撞雷达测量主车与目标车之间的距离，同时获取相对速度以及相对方位角等信息，并将其传送给系统的控制单元进行处理。毫米波雷达相比于其他测量介质雷达(如超声波雷达、红外雷达、激光雷达)具有探测距离远、运行可靠、测量性能受天气等外界因素的影响较小等优点，最适合应用于汽车防撞雷达应用。毫米波汽车防撞雷达还处于实验研究阶段，除成本问题外，另一个重要原因就是虚警问题，如邻近车道上的车辆产生的虚假信号。这要求防撞雷达必须具备测角能力，目标的方位角信息对于减少虚警是必不可少的［1］。本文结合国内外毫米波汽车雷达研究进展，从提高工作频段、雷达波形设计、超分辨数字波束形成方法3个方面入手，探讨提高系统方位角分辨率和多目标识别能力以减少虚警。

1 提高雷达工作频率

当前毫米波汽车雷达工作频段主要集中在24 GHz和77 GHz，随着亚毫米波和太赫兹器件及系统的发展，100 GHz以上的雷达系统渐渐成为研究热点。通过采用更高的频率，可使汽车雷达小型化，并可提高方位角分辨率和距离分辨率。

1.1 小型化

典型的汽车雷达传感器尺寸约10 cm×8 cm×6 cm，安装在车体内仍然占用较大空间。提高工作频率，可以缩小天线尺寸，节省空间。以贴片阵列天线为例，根据天线理论，一个贴片单元的宽度为1/2波长。150 GHz频段下16单元贴片阵列与77 GHz 4单元贴片阵列尺寸相同，如图1所示。所以同样尺寸的天线，150 GHz雷达系统可以比77 GHz得到更高的性能。如果两个天线单元数目相同，在保持同样性能的情况下，150 GHz雷达系统的体积约为77 GHz的1/4。

图1 77 GHz和150 GHz频段贴片阵列对比

1.2 方位角分辨率

雷达天线孔径越大，频率越高，横向或方位角分辨率越高。如图2所示，假设77 GHz雷达天线孔径宽度为5 cm，距雷达50 m的横向分辨率为4.2 m。此时的方位角分辨率为2.4°，而相同孔径宽度在相同距离时，150 GHz雷达的横向分辨率可以达到2.1 m，方位角分辨率 1.2°，可得到更好的单目标检测能力。

图2 77 GHz和150 GHz横向分辨率对比

1.3 距离分辨率

雷达系统的距离分辨率取决于调频连续波(frequency modulated continuous wave，FMCW)雷达的带宽。当前，77 GHz雷达传感器可实现4 GHz带宽，3.8 cm的距离分辨率。150 GHz雷达可实现8 GHz带宽，距离分辨率小于1.9 cm。因此，可提高测量精度和多目标分辨能力。

2 雷达波形设计

雷达的波形选择要充分考虑抗干扰性和可实现性、多目标识别以及回波处理中算法的快速简单性。FMCW方式具有适于探测近距离目标，具有峰值功率低、射频结构简单、测量时间短等优点。因此，它一直是汽车防撞雷达的首选。但其缺点也很明显，如:线性调频度不易获得，导致距离分辨率变坏;多目标场景下，三角波调制调频连续波会产生虚假目标，从而影响防撞雷达的工作性能。

2.1 FMCW 原理

FMCW雷达的基本原理是发射信号通过三角波或锯齿波频率调制，利用发射和回波信号之间的频率差确定目标距离(如图3所示)，当前方目标有相对速度时，信号的回波含有频移，通过对中频信号的处理即可获得目标的相对速度和相对距离的信息。

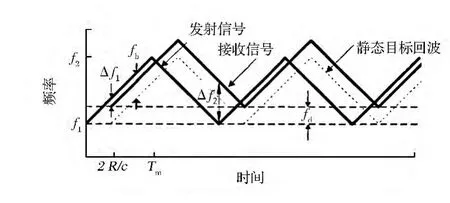
图3 FMCW雷达目标回波信号

在发射信号的上升段和下降段，回波中频输出信号为

式中:f0为发射信号中心频率;B为频带宽度;R为相对距离;Tc为扫频周期;V为相对速度;c为光速。

根据式(1)、(2)，可以获得前方目标的相对距离R和相对速度V为

上述过程可等价为在距离—速度(R—V)平面内确定两个斜率为相反的直线(如图4所示)，从而可以获得一个交点即为真实的目标信息点，如此即可确定目标的相对速度和距离信息。在单个目标的情况下，FMCW雷达表现了很好的目标检测性能。在实际道路环境中，雷达的探测范围内经常会出现多个目标车辆，此时三角波调制方式不能满足多目标识别的目的，会产生虚假目标(如图4所示)。

图4 虚假目标的产生

2.2 FSK+FMCW 体制

频移键控(frequency shift keying，FSK)体制又称双频测距法［2］，交替发出两种频率的电磁波，可接收到两个具有不同多普勒频率的回波。通过两个回波的多普勒频率差和相位差可得到相对速度和距离。FSK体制雷达信号频带窄，调制波形简单，可同时捕捉多个运动目标，系统实现简单，成本比FMCW体制要低很多。缺点是不可以探测相对静止的目标(相对静止的目标没有多普勒频移)，系统响应比较慢，多用于测速雷达。

FSK+FMCW体制［3］结合了上述两种体制的优点，试图解决雷达多目标辨识和算法的实时性问题。FSK+FMCW发射波形如图5所示，图中:fshift为A段和B段的频移;finc为A段或B段的频率步进增量;BW为频带宽度;N为A段或B段的波段个数。其思路是频率按线性规律步进，A段和B段如图所示交替发射，接收机将回波信号变为基带信号，在每个A段、B段信号结束处进行采样。通过分别对A段和B段进行快速傅里叶变换，同一目标可以获得相同的中频信号k=kA=kB，从而它们在距离—速度平面内为相同的直线，但相位角则为相互不同的ΦA、ΦB。其中含有目标的相对速度和相对位移信息。因此，ΔΦ =ΦA－ΦB可以通过下式求得

图5 FSK+FMCW波形

在距离—速度平面，由A段和B段的频率信息和相位差信息可无模糊地确定目标的速度和相对距离，可避免虚假目标的产生。

FSK+FMCW体制波形对比FMCW具有测量时间短，算法和目标信息计算简单，并且具有多目标识别能力。同时也克服了FSK方式不能分辨相对静止目标的缺点，具有很高的实用价值。

3 超分辨数字波束形成

77 GHz传感器的方位角分辨率通常在2°～5°。为了进一步提高方位角分辨率，可应用超分辨数字波束形成方法。

一个典型的数字波束形成(digital beamforming，DBF)阵列雷达前端架构如图6所示。信号源输出FMCW信号给发射天线。同时，一部分发射信号作为本地振荡信号与一组天线阵列接收的信号混频，将接收信号下变频到基带射频信号，通过A/D，送到数字信号处理器中进行阵列数字信号处理。

传统的阵列处理方法利用阵列波束形成进行空间扫描，对于一定的阵列合成尺寸，其空间分辨率受瑞利限的限制。超分辨阵列信号处理方法的目的是检测空间辐射源并进行测向和定位，突破瑞利限的限制。典型的超分辨阵列信号处理方法有多重信号分类(multiple signal classification，MU-

为了增强相互靠近的多目标识别能力，要求汽车雷达传感器的方位角分辨率越高越好。传统的波达方向(direction of arrival，DOA)估计方法如单脉冲技术或空间功率谱测量技术，其方位角分辨率固定为半功率波束宽度:SIC)算法［4］。

图6 数字波束形成的结构示意

MUSIC算法对多天线阵列接收的含噪信号进行子空间分解。通过对均匀线性阵列接收信号自相关矩阵的特征值分解可得到噪声子空间和信号子空间，进而得到目标的DOA估计。

假设采用均匀天线阵列m元天线对p个目标信元在二维空间进行测向的问题。阵元间距d=λ/2，有p个互不相关的窄带信号源平面波辐射到线阵上，信源方向分别是 θ1，θ2，…，θp。在阵元第n次采样的时候，得到基带数据为

式中:A=［α(θ1)，α(θ1)…，α(θp)］为阵列导向矢量;S(n)为待求结果;U(n)为加性噪声。

接收信号的协方差矩阵为

对Rxx进行特征值分解，可分解为相互正交的信号特征向量和噪声特征向量。

式中:Vs和Λs分别为源信号的特征向量和特征值;Vn为噪声特征向量。

因为，VnHα(θ)=0，构造如下空间谱函数:

谱函数最大值所对应的θ就是信号源方向的估计值。

MUSIC算法的一个重要步骤是子空间估计，即通过计算空间相关矩阵的特征分解。信息理论准则如 MDL或 AIC可用于估计信号的数量［5］。如果子空间估计失败，DOA估计将给出错误的结果，如目标角度错误，或未发现目标，这会大大降低防撞雷达的可靠性。提高信噪比、入射信号去相关以及天线阵列失配校准是能否成功进行子空间估计的重要因素。

相关研究实验结果［6］表明，77 GHz防撞雷达实验平台基于MUSIC超分辨DBF方法所获得的方位角分辨率比传统DBF方法(如Bartlett波束形成)大约高3倍，达到1.7°。基于 MUSIC超分辨DBF方法能大幅提高方位角分辨率，具有非常好的应用前景。

4 结语

针对目前汽车防撞雷达高性能、低虚警的设计要求，本文主要从雷达工作频率、波形设计以及超分辨数字波束形成体制3个方面进行研究，提高雷达工作频率可获得更高的分辨率和更小的体积;通过对FSK和FMCW两种基本方式进行综合，可以得到性能更优的FMCW+FSK雷达信号，实现多目标分辨;基于MUSIC超分辨DBF方法可提高阵列天线固有的方位角分辨率，具有非常好的应用前景。

［1］ 张建辉，刘国岁，顾红，等.编码步进调频连续波在汽车防撞雷达中应用［J］.电子学报，2001，29(7):943-946.

［2］ Artis，Jean P，Henrio，et al.Automotive radar development methodology ［C］//International Conference on Radar Systems.Brest，France，1999.

［3］ Klotz M，Rohling H.24 GHz radar sensors for automotive applications［C］//International Conference on Microwaves and Radar.Wrociaw，Poland，2000.

［4］ Ralph O，Schmidt.Multiple emitter location and signal parameter estimation［J］.IEEE Trans.Antennas and Propagation，1986，34(3):276-280.

［5］ Mati W，Thomas K.Detection of signals by information theoretic criteria［J］.IEEE Trans.Acoustics，Speech，and Signal Processing，1985，33(2):387-392.

［6］ Steinhauer M，Ruo H O，Irion H，et al.Millimeter wave radar sensor based on a transceiver array for automotive applications［J］.IEEE Trans，Microwave Theory and Techniques，2008，56(2):261-269.