高校教师教学评价系统指标及其权重取值

庞国楹，刘 俊，魏 杰

(军事交通学院基础部，天津300161)

在我国高等教育迅速发展的今天，提高教育质量是学校的首要工作。提高教育质量的有效途径是提高教育工作者的整体素质，教学评价对其起到积极的监督和促进作用。国外较著名的独立教学评价系统软件有Question Mark、Rubric Star和Smart等，但是这些软件对教学过程和评价过程一体化支持的能力不高，或者由于过于强调与具体教学过程的整合性而失去了对不同教学理论和教学内容的支持弹性。我国高校教学评价的评价指标多以评价教师的有效教学行为为特征，缺乏潜在因素(如创造性、主体性等)的弹性指标，并且很多高校都是用同一份评价表评价所有学科、所有教师的教学，缺乏针对性，因此应进一步完善教学评价的评价指标体系，以适应不同的教学需要［1－2］。高校的教学评价一般由3部分组成:专家评价、同行教师评价和学生评价;然而，各高校三方评价所占的百分比不尽相同，评价易流于形式，有失公允［3］。在我国高校实际操作中，应建立以学生为主体、专家与领导全部共同参与的评价模式，有机结合3个方面评价优势，科学配置比例，对教师的特殊劳动进行评价。

针对以上问题，本文首先依据动态教学评价理论和层次分析法，通过学生评价体系、专家评价体系和领导评价体系的有机结合，构建合理的教学评价系统;并在对教师教学充分调研和分析的基础上，利用该系统重点研究教师教学评价模型，以及如何科学分配三方评价所占比例。

1 教学评价体系

1.1 传统教学评价方法存在的问题

随着传统的教学评价系统研究地深入，除了对专家评价法、模糊评价法和层次分析法的应用和改进，对评价指标的研究也趋于更加具体和详细［4］，但依然面临着一些问题。

(1)对于同一位教师的教学评价，现在一般只涉及到学生、专家和领导根据指定的指标进行打分，但是没有考虑到两个问题:指标一般采取同一个指标集合，并没有考虑到学生、专家和领导是具有一定偏好的;从概率论角度来讲，三者打分的结果应该偏差不大，即方差最小。

(2)对不同教师进行教学评价的过程中，一般只考虑简单的分数差异，并没有从统计学角度分析，要能排出合理的名次，应该使得差异性更大，即不同教师之间的方差应该最大。

(3)传统的评价过程中，如果出现结果不理想状态时，一般都怀疑可能是指标选取不合理或者分数不合理。随着研究不断深入，指标体系基本已经成型，学生、专家和领导的打分是比较合理的，而且重新打分也是不现实的。如何基于一定的目的性对权重进行选取和改进，是以往研究中存在的缺陷。

1.2 教学评价指标体系的选取

由于学生、专家和领导所处的社会地位不同，对教学评价理解的角度不同。现有的模糊评价方法中一般采用不同的偏好函数，但是在实际问题中，偏好函数的选取是相当困难的。相对简单的解决办法是将学生、专家和领导的不同偏好体现在不同的评价指标体系中，所以，在评价体系设计过程中，建立不同的指标体系是非常有意义的。比如:从学生角度，更关注于课下是否辅导以及效果、讲课是否新颖有趣、总体收获和掌握的程度多少等;从专家角度，更关注于讲授重点是否突出、教学方法使用是否合理和多样、是否根据学生具体情况因材施教、上课过程中是否与学生互动等等;从领导角度，更关注于是否与实际相结合、语言是否简洁易懂、是否将所有的教具充分利用、课堂纪律如何等。部分指标见表1。

表1 部分教学评价系统指标

2 权重选取模型

结合层次分析法的思想和教学评价的实际背景，假设评价系统中评价指标以及学生、专家和领导的打分是合理的，不存在恶意打分的情况;如果存在恶意打分的现象，应该进行数据处理，将不合理分数剔除。

模型1 学生、专家和领导对一位教师的评价差异最小，即三者评分的方差最小，根据概率论和数理统计的相关理论确定指标权重，建立模型如下:

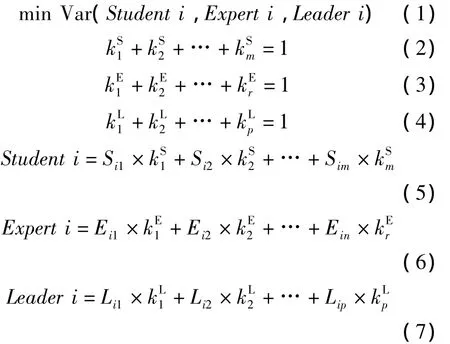
式(1)为学生、专家和领导对一位教师打分的差异度最小，即方差最小;式(2)中为学生的 m 个评价指标;式(3)中为专家的 r个评价指标;式(4)中为领导的 p 个评价指标;式(5)中为学生对某位教师在每个指标分项上的打分，Student i为学生对某位教师的总体打分;式(6)中，Ei1，Ei2，…，Eir为专家对某位教师在每个指标分项上的打分，Expert i为专家对某位教师的总体打分;式(7)中，Li1，Li2，…，Lip为领导对某位教师在每个指标分项上的打分，Leader i为领导对某位教师的总体打分。

模型2 为了更好地将不同教师之间的差异体现出来，并能合理地进行排序，建立模型如下:

式(8)为n个教师分数的差异，即方差最大;式(9)中，学生、专家和领导的权重分别为λS、λE和λL;式(10)中，goal i为第i个教师的总得分。

模型1描述了对同一名教师的评价满足方差最小的目标下，各项指标的权重选取方法;模型2描述了对不同教师间的评价满足方差最大的目标下，学生、专家和领导的权重如何选取。该种方法可以体现出:

(1)不同偏好对指标和模型的影响;

(2)可以增加指标选项，模型保持不变并且能够多次仿真选出合理的权重;

(3)避免重复打分造成的不必要的麻烦;

(4)保持对某位教师的打分不会产生太大差异，而且也能将不同教师之间的差异性表现出来。

模型1和模型2的评价方法在保持传统评价一致性的基础上，对传统的专家评价方法、层次分析方法进行了相应的改进。

3 实例分析

根据中国学术期刊论文数据库和万方数据库关于教学评价的相关论文，结合实际情况，选取100名学生，对应指标10个;10名专家，对应指标8个;5名领导，对应指标6个。学生、专家和领导的打分在85～100、90～98和95～100分间随机赋值，这样可以避免恶意打分的情况。

表2为学生评价指标、专家评价指标、领导评价指标在系统运行6次后的结果。从整体来看其残值较小，在接受范围之内。学生的10个评价指标的权重数据取值是比较均匀的，说明学生的评价指标选取比较合理。在专家评价指标中第7个指标的权重最大，第4个指标的权重最小;领导评价指标中第3个指标的权重最大，第4个指标的权重最小，这说明专家和领导的指标选取具有一定偏好性，这是符合现实的。

表3为学生、专家和领导的打分权重分配在运行11次后的结果。方差取得最大值0.993 1时，学生的打分权重为0.506 5，专家的打分权重为0.293 1，领导的打分权重为0.200 4;方差的均值为0.975 3，此时学生的打分权重为0.417 0，专家的打分权重为 0.384 0，领导的打分权重为0.199 0。这说明在教学评价体系中学生的权重应该最大，领导最小，专家偏中，这与实际情况相符。

表2 每个分指标权重选取范围

指标 运行1 运行2 运行3 运行4 运行5 运行6均值k E1 0.155 231 0.155 439 0.108 432 0.066 036 0.115 181 0.067 676 0.111 333 k E2 0.109 635 0.109 577 0.105 824 0.049 955 0.111 467 0.159 527 0.107 664专家评价指标k E3 0.247 649 0.248 126 0.056 920 0.142 716 0.135 758 0.135 364 0.161 089 k E4 0.070 831 0.070 705 0.090 208 0.040 879 0.024 254 0.046 987 0.057 311 k E5 0.074 589 0.074 695 0.228 264 0.118 001 0.142 925 0.139 851 0.129 721 k E6 0.206 323 0.206 000 0.052 671 0.138 057 0.101 770 0.107 409 0.135 372 k E7 0.067 631 0.067 425 0.273 793 0.287 703 0.198 005 0.078 988 0.162 258 k E8 0.068 110 0.068 033 0.083 887 0.156 654 0.170 640 0.264 197 0.135 254 k L1 0.152 180 0.152 640 0.023 030 0.209 506 0.145 199 0.218 226 0.150 130领导评价指标k L2 0.196 829 0.196 249 0.167 868 0.011 421 0.084 219 0.121 604 0.129 698 k E3 0.181 676 0.181 912 0.255 865 0.218 870 0.418 158 0.301 252 0.259 622 k L4 0.021 780 0.021 761 0.037 045 0.054 853 0.020 252 0.187 562 0.057 209 k L5 0.192 835 0.193 046 0.354 561 0.221 443 0.045 416 0.070 055 0.179 559 223 781残值/10 －9 4.63 4.63 4.67 5.25 4.96 4.69 4.81 k L6 0.254 699 0.254 393 0.161 632 0.283 907 0.286 756 0.101 301 0.

4 结语

本文利用层次分析法，根据学生、专家和领导具有不同的偏好，构建了基于不同偏好的教学评价系统。根据评价系统一致性原则，建立了学生、专家和领导针对一名教师的打分评价方差最小的模型1，为能够充分将不同教师的教学差异区分出来，建立了不同教师之间的打分评价方差最大的模型2。通过多次仿真模拟，对比运行的结果给出了评价指标以及学生、专家和领导三者之间的合理的比例权重。

［1］ 李春玲.高校教师教学水平评价在我国的实践发展和理论探讨［J］.现代教育科学，2005，22(7):79-81.

［2］ 朱泓.高等学校教学质量评价体系的研究［D］.大连:大连理工大学，2004.

［3］ Felix T S，Kumar C N.Global supplier development considering risk factors using fuzzy extended AHP-based approach［J］.O-mega，2007，35(4):417-431.

［4］ Combarro E F，Miranda P.Identification of fuzzy measures from samples data with genetic algorithms［J］.Computer ＆ Operations Research，2006，33(10):3046-3066.