压放频率对超声弹性成像结果的影响研究

李秋萍，陈 科，林江莉

(四川大学 材料科学与工程学院，成都 610065)

·热 点 研 究·

压放频率对超声弹性成像结果的影响研究

李秋萍，陈 科，林江莉

(四川大学 材料科学与工程学院，成都 610065)

为了探讨压放频率对压迫式超声弹性成像结果的影响，文中采用外置激振器产生不同的频率来振动组织，超声探头同步采集RF回波信号，通过位移估计和应变估计获得其连续应变场图像。实验结果表明：临床上由于采用瞬时组织应变进行成像，不同的压放频率对成像结果将造成影响；应变幅值在频率增大的同时会逐渐减小，将影响成像的对比度，应变均值在频率变化时能保持较好的稳定性，在不同组织之间的差异也较明显。采用应变均值成像相对于瞬时应变更具有临床参考意义。

超声弹性成像；压放频率；应变；弹性模量；激振器

生物组织的力学特性对于疾病的诊断具有非常重要的参考意义。长期的临床实践表明，组织的病理变化通常会引起其力学特性的改变。以检测生物组织弹性模量为目的，Ophir等[1]于1991年提出压迫式弹性成像技术，经过长期的发展和不断的优化完善，作为一种新兴的医学成像诊断方法，现已被广泛应用于超声成像设备，并在乳腺肿瘤及前列腺癌等疾病的诊断中起到重要的作用。

压迫式弹性成像技术通过对组织施加压力，获取压缩前后的回波信号进行互相关处理，估算出组织的位移变化，进一步获得组织的应变图像，以此间接反映组织的弹性信息。压迫振动作为外界干预手段，压迫过程受人为控制。其压力大小及压放频率是否会对超声弹性成像结果产生一定的影响是值得研究的问题。但是，目前这方面的研究较少，更缺乏定量研究。

罗葆明等[2]2007年采用UE评分法探讨了乳腺超声弹性成像检查压力与压放频率对诊断结果的影响，得出乳腺超声弹性成像检查时应选择压力与压放频率为2～3时进行评分。邱少东等[3]2013年在睾丸弹性成像实验中探讨了感兴趣区域应变均值与压力大小及压放频率之间的关系，得出中等压力、中-高频压放得到的超声图像更稳定。上述的研究表明，压力大小及压放频率会对超声弹性成像结果产生一定的影响。但是这些研究均是在超声仪获得的弹性图像的基础上进行的，其压迫过程仍然是人为施力，振动频率和振幅不确定，其数据不具有客观性。

为了定量分析压放频率对超声弹性成像结果的影响，本文采用专业的振动设备，在材料承受范围之内，在确定的频率数值下对组织进行压迫振动，施压过程中保持恒定的振幅，采集对应的RF回波信号，分析出组织的应变信息。而弹性图像实际上是应变图像彩色编码后的结果，振动频率与应变之间的关系可反应振动频率对压迫式弹性成像结果的影响。

1 方法

1.1 实验装置

为了获得精确的振动频率，本文采用如图1所示的外部振动实验装置。在前端的信号发生器中产生一个确定频率的正弦信号，通过功率放大器进行增益放大，放大后的信号传入激振器使其振动，并将该振动传递到待测组织或材料，超声探头在振动的同时采集RF回波信号。为保证振动时所产生的压力幅值不变，在改变振动频率时，功率放大器选择的放大倍数应保持不变。

图1 外部振动实验装置示意图

1.2 位移估计

(1)

式中：gj(i)表示第j条RF信号上第i点样本，且满足i=1，2，…，m及j=1，2，…，n；纵向位移ai和横向位移li分别满足

amin≤ai≤amax，lmin≤li≤lmax

在动态编程弹性成像算法中，将位移连续性的先验信息与幅度相似性结合起来，提出了一个约束位移变化的代价函数。第j条RF信号的位移连续性约束为：

(2)

式(2)将第i点样本的位移逼近第i-1点的位移，αa和αl分别表示纵向和横向的权重因子。因此，第j条RF信号上第i点样本的代价函数可以定义为：

(3)

式中：da,dl分别表示使代价函数取得最小值的纵向位移和横向位移，通过M函数可将每个样本点的da和dl记录下来。

(4)

计算从第1点样本到第m点样本的代价函数，根据第m点样本计算出的最小代价函数值可获得该点的位移值，同时回溯到第i点样本，则i=1，2，…，m的位移值在递归过程中便可获得：

(5)

为加快成像速度，可对压缩前的RF信号gj(i)进行降采样，得到新的RF信号gsj(i)，并与压缩后信号进行位移估计，对相邻两点位移数据线性插值即可获得整个位移场数据。算法原理如图2所示。

图2 二维动态编程算法原理

图2(b)中，白色表示代价值低，黑色表示代价值高。

1.3 应变估计

位移不能直观地反映组织形变的情况，通过应变估计得到的应变图能清楚地展示组织的病变区域，同时能更好地表征组织的弹性信息。利用最小二乘法进行应变估计，Dj(i)为位移场中第j列第i行的数据，选取该点附近长度为2k+1的位移窗口，即第j列第i-k行到第i+k行之间的位移，对窗口内的2k+1点位移数据进行最小二乘拟合[5]：

(6)

dj(h)为第h点的组织深度，拟合出的z即为第j列第i行的应变值。此时得到的应变图像受拟合点数的影响，会引入大量的噪声，对应变图像的横向方向进行卡尔曼滤波[6]可得到较平滑的应变图像。

假设εi，j是含有噪声的应变图像zi，j的原始图像，rj和sj分别表示过程噪声和量测噪声，则

εi，j=εi，j-1+ri，j

(7)

zi，j=εi，j+si，j

(8)

可得到先验应变估计Ti，j及其方差Qi，j：

Ti，j=ti，j-1

(9)

(10)

式中：σr为过程噪声的方差，可通过zi,j及zi,j-1的8-邻域均值得到：

(11)

后验应变估计ti，j及其方差qi，j则为：

(12)

(13)

通过先验估计和后验估计的交替进行，最终的应变场便可获得。

2 实验结果及分析

实验采用CIRS公司生产的弹性成像phantom体模。该体模是一款专用于超声弹性成像研究的仿体模型，其力学特性不受温度变化的影响，仿体中含有4种不同弹性的球体模型，每种弹性的小球又有直径为10mm和20mm的两个。球体模型I到球体模型IV所示的弹性模量依次为：10kPa、18kPa、58kPa、111kPa，背景材料的弹性模量为28kPa。实验采用超声探头中心频率为5MHz，采样频率为40MHz，此时体模中声速为1 540m/s，声衰减系数为0.50dB/cm。实验中所使用的超声仪器的采集帧频为23～26帧/s，保持振动幅度不变，在不同的振动频率下分别对体模中4种类型的直径20mm的小球进行压迫，采集对应连续100帧RF回波信号。

2.1 应变随时间的变化

对phantom施加确定幅度和频率的正弦振动，通过前面提到的方法，对相邻两帧RF回波数据进行应变估计，可得到连续的应变图像，如图3所示。图3中的两条曲线分别对应背景材料和模型I在压迫频率为5Hz时的应变。由图3可以看出，两条应变曲线成周期性变化，但振幅不完全恒定；同时由于仿生物组织的材料并不是纯弹性材料，两种不同材料即使受到相同压力，其应变曲线也不会完全匹配，而会产生一定的时延。图3中可以明显地看到两条曲线具有交叠。

图3 应变-时间曲线

上述现象说明，目前临床中仅选择某一瞬时的应变值来成像可能具有随机性和片面性。由于不同时刻获得的应变值不同，所以成像的结果也不相同，该结果图像可能并不能反应组织弹性的真实情况。

2.2 频率对成像结果的影响

实验中考虑到临床操作中的频率范围，将正弦振动的频率范围设定于1～10Hz之间，且间隔频率为1Hz。在振动幅度相同的前提下，对球体模型采用不同的振动频率进行压迫成像。在球体模型IV的振动频率为1Hz、4Hz、7Hz、10Hz的连续应变中任意选取某一时刻的应变成像结果，如图4所示。根据成像结果可见，不同压迫频率下获得的成像结果不同。因此，采用不同的压迫频率会造成背景材料与球体模型的应变之间对比度不同，成像出来的球体形态也有所不同。

图4 球体模型IV的应变估计图

2.3 应变均值与频率的关系

由图3可知，应变大小随时间变化，而采用瞬时应变进行成像具有随机性，即使压放幅度和频率相同，获得的弹性图像也可能不相同。鉴于此，本文研究了运用应变均值进行弹性成像的效果。

图5 不同组织模型中应变均值与频率的关系

选择球体模型中大小为20×200pix的区域作为感兴趣区域(regionofinterest，ROI)，计算不同频率下ROI区域100帧回波信号的应变均值，结果如图5所示。可见，当频率在1～10Hz之间变化时，应变均值虽然有一定的波动，但波动范围不大；同时均值之间的间隔也与小球弹性模量之间的差别对应，能较好地区分弹性模量不同的模型。可见，如果采用应变均值进行弹性成像更具有稳定性和准确性，成像结果更接近组织的真实弹性模量。

2.4 应变幅值与频率的关系

四种模型中应变幅值随频率变化的曲线，如图6所示。可见，尽管在所有实验过程中，我们始终保持外部激振器施压的幅度不变，但是不同粘弹性模型的应变幅值却是不同的，并且同一粘弹性模型的整体应变幅值也随着频率的增大而减小。纯弹性材料的幅度不会随频率变化而变化，不同材料应变幅值的差异以及同一材料不同频率下应变幅值的差异反映出组织的粘性特征。当引入频率这一影响因素时，其中包含的粘性信息也在连续应变图像中表现出来。这将为下一步利用此频率特性，对组织的粘性特征成像奠定基础。

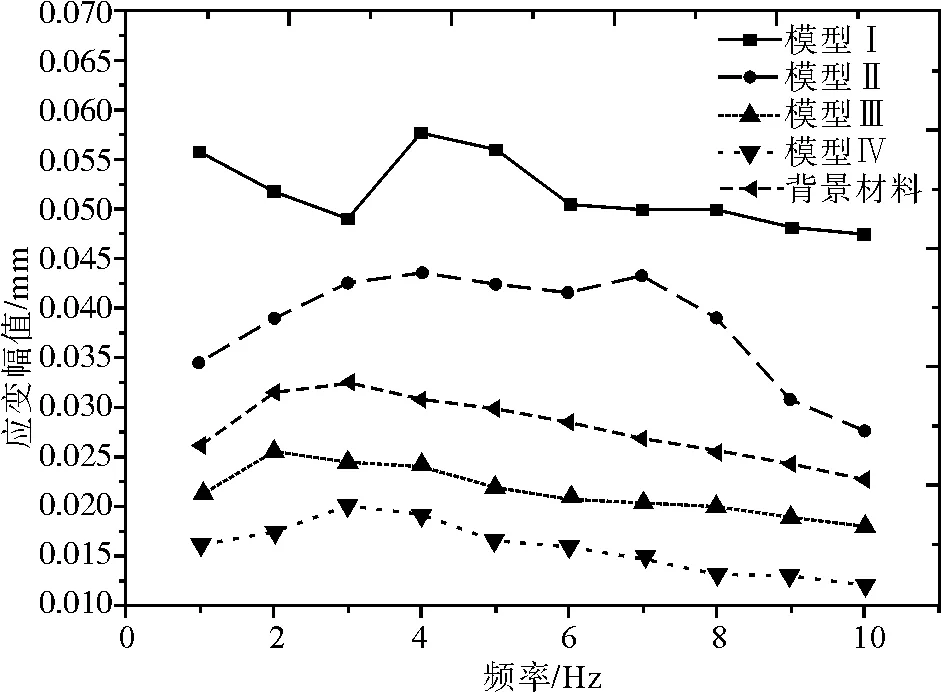
图6 不同组织模型中应变幅值与频率的关系

3 结束语

本文在压迫式弹性成像的基础上，采用激振器对材料施压，保持压力幅度不变，对仿体模型施加不同的振动频率后，采用二维动态编程算法对回波信号进行位移估计及应变估计获得连续应变图像。

目前，临床上获得的超声弹性图像，实为瞬时应变成像。实验获得的应变-时间曲线说明采用瞬时应变成像，其结果具有随机性和不确定性。研究还发现，对连续应变取平均得到的应变均值相对于瞬时应变能更好地表征组织的弹性特性。而不同频率下材料最大应变幅值的变化则反映了组织包含的粘性信息对成像结果的影响。

对于压迫式超声弹性成像技术，压力的施加及组织的应变情况都符合动态粘弹性理论[7]。根据这两个参数我们可以进一步获得复模量与频率之间的关系，复模量相对于应变能更直观地给出不同力学模型下材料的弹性模量和粘性系数。应力曲线保持不变时，当应变幅值随频率增大不断减小，复模量反而会随频率增大而增大。纯弹性材料的复模量不会随频率变化而变化，而具有粘性的材料的复模量则对频率比较敏感。在接下来的研究中将尝试从粘弹性材料中提取粘性系数。

[1]OphirJ,CespedesI,GarraB,etal.Elastography:ultrasonicimagingoftissuestrainandelasticmodulusinvivo[J].Eur.J.Ultrasound.，1996(3):49.

罗葆明,曾婕,欧冰,等. 乳腺超声弹性成像检查压力与压放频率对诊断结果影响[J]. 中国医学影像技术,2007,23(8):1152-1154.

邱少东,陈菲,曾碧丹,等. 压力大小及压放频率对正常睾丸超声弹性声像图影响的析因设计研究[J]. 中国临床医学影像杂志,2013,24(5):349-352.

RivazH,BoctorE,ForoughiP,etal.Ultrasoundelastography:adynamicprogrammingapproach[J].IEEETrans.Med.Image.,2008,27(10)：1373-1377.

袁金伟. 超声弹性成像中的位移和应变估计[D]. 杭州: 浙江大学,2012.

RivazH,BoctorE,ChotiM,etal.Real-timeregularizedultrasoundelastography[J].IEEETrans.Med.Imag., 2011,30(4):928-945.

杨挺青. 粘弹性力学[M]. 武汉： 华中理工大学出版社，1990.

Influence of Compression Frequency on Ultrasound Elastography

LI Qiuping， CHEN Ke， LIN Jiangli

(Department of Materials Science and Engineer College, Sichuan University, Chengdu 610065, China)

The effect of frequency on the imaging was focused by this paper, an external vibrator which generated sine signals with different frequency were used to compress tissues, then a set of RF echo data were received by ultrasonic transducer. The continuous tissue strain field was obtained by motion estimation and strain estimation. The elastograph is obtained clinically as instantaneous strain imaging, thus the frequency of compression will affect the imaging results. The amplitude of strain decreased with the increasing of frequency, which will affect the image contrast. The results also showed that the mean of continuous strain could remain stable when frequency changed, which showed obviously different for different tissues. Compared with instantaneous strain, the mean of continuous strain has more profoundly clinical application significance.

ultrasound elastography; compression frequency; strain; elastic modulus；vibrator

2014-11-12；修改日期: 2014-12-10

国家自然科学基金资助项目(81301286；30970781);四川省科技支撑基金资助项目(2014GZ0005)。

李秋萍(1989-)，女，硕士，研究方向:医学图像处理。

林江莉(1971-)，女，博士，副教授，研究方向：图像处理。

Q-334

B

10.3969/j.issn.1672-4550.2015.04.064