基于小波变换的台风激励下千米级斜拉桥模态参数识别

茅建校 王 浩 程怀宇 李爱群

(东南大学混凝土及预应力混凝土结构教育部重点实验室,南京210096)

基于小波变换的台风激励下千米级斜拉桥模态参数识别

茅建校 王 浩 程怀宇 李爱群

(东南大学混凝土及预应力混凝土结构教育部重点实验室,南京210096)

为了给大跨桥梁结构损伤识别和安全性评价提供现实依据,采用小波变换(WT)方法进行千米级斜拉桥的模态参数识别研究.以“海葵”台风激励下的苏通大桥为研究对象,基于结构健康监测系统(SHMS)采集的数据,采用WT方法共识别出包括频率和阻尼比在内的主梁前4阶竖弯模态参数、前2阶扭转模态参数和第1阶侧弯模态参数,并将结果与相关文献提供的模态参数进行对比;在此基础上研究了海葵台风期间该桥主梁模态参数的全过程变化情况.结果表明:基于WT的模态参数识别方法稳定可靠;随着时间的变化,主梁各阶模态频率均较稳定,而模态阻尼比的波动则较明显.

台风;苏通大桥;小波变换;频率;阻尼比;参数识别

准确估计大跨桥梁结构的模态参数,可以为结构有限元模型修正、损伤识别、振动控制等工作奠定基础,具有重要的研究意义和应用价值[1].现有的模态识别方法主要分为人工激励法和环境激励法2种.相对于人工激励方法而言,环境激励法具有无需对结构进行激励、费用节省、安全性好、识别精度高等优点,在参数识别领域内的运用越来越受到重视[2].目前,常用的环境激励下模态参数识别方法主要包括随机子空间法(SSI)、希尔伯特-黄变换(HHT)法和小波变换(WT)方法等.其中,SSI法是一种整体拟合的时域模态分析方法,但环境激励振动的采样时间往往较长,识别计算量大,且如果Hankel矩阵阶数选择不当,易造成模态丢失或虚假模态等问题[3].HHT法是一种新兴方法,但存在着自身缺陷,如经验模态分解法(EMD)频率分辨率不高、模态混叠和边缘效应等问题尚未解决、识别结果误差较大等[4].WT方法凭借其良好的时频分辨率,可实现多自由度系统低频密集模态的自动解耦,国内外学者对利用WT法识别结构模态参数进行了大量研究[5-8].然而,利用WT方法对千米级斜拉桥等具有超低频密集模态的结构进行模态参数识别的研究却鲜见报端,对基于现场实测的强台风激励下大跨度桥梁模态参数演变特性的研究也不多见.为此,本文基于苏通长江公路大桥(简称苏通大桥)结构健康监测系统(SHMS)中振动监测子系统采集的数据,针对“海葵”台风激励下大桥主梁跨中实测的加速度响应,采用WT方法识别主梁模态参数,并分析模态参数随时间的变化规律,以期掌握台风期间苏通大桥动力特性的全过程变化特点,同时为大跨度斜拉桥的抗风设计和研究提供参考.

1 工程背景

苏通大桥主跨1 088 m,2008年建成通车时为世界第一大跨度斜拉桥,是我国建桥史上工程规模最大、综合建设条件最复杂、科技含量最高的现代化特大型桥梁工程之一.苏通大桥结构刚度低，自振周期长,对风荷载的作用较为敏感,为了评估和预测各种灾害影响下的结构健康状态、保证大桥在设计使用寿命内的运营安全,该桥建立了较为全面的SHMS,其主梁布置的加速度传感器如图1所示.

图1 苏通大桥主梁振动传感器布置图(单位:m)

2012年8月8日,第11号台风“海葵”正面袭击了长三角部分地区,给当地造成了巨大的经济损失和人员伤亡,苏通大桥也在影响范围之内.该桥的SHMS系统中振动监测子系统全程记录了台风期间大桥主梁、主塔和拉索关键截面的振动响应,为模态识别研究提供基础.

2 基于WT的模态参数识别方法

2.1 连续小波变换

小波是指在时域内具有紧支性的、长度有限、均值为零的波形,记为ψ(t),其中t为自变量.对其进行伸缩和平移得到对应小波函数族ψa,b(t),则

(1)

式中,a>0为尺度参数;b为平移参数.

小波变换的实质是利用小波函数族ψa,b(t)与待分析信号卷积,得到一系列可以表征信号时频分布特性的小波系数.故将连续小波变换定义为

(2)

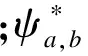
2.2 多自由度系统的模态参数识别

一个n自由度系统自由衰减振动信号可表示为

(3)

式中,Bk为初始幅值;ξk为系统第k阶阻尼比;wdk为系统第k阶圆频率;ψ0k为第k阶初相位.

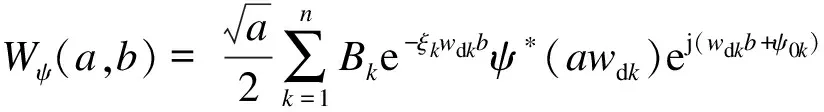
(4)

(5)

式中，ak为第k阶圆频率对应的尺度参数.

总体而言,小波变换提供了一种对多自由度自由振动系统进行模态解耦的方法,系统的第k阶圆频率wdk及阻尼比ξk可由下式求得:

(6)

arg[Wψ(ak,b)]=wdkb+ψ0k

(7)

2.3 小波函数及相关分析参数

小波变换的时频分辨率依赖于母小波ψ(t)及其相关参数的选择[6].本文采用Complex-Morlet小波作为母小波进行小波变换,其在时域内的函数形式为

(8)

式中,fb为带宽参数,起控制小波形状的作用;fc为中心频率.为了满足模态分离需要的频率分辨率、加强对端点效应的抑制效果,中心频率以及带宽参数需满足下式:

(9)

式中,fk为第k阶模态频率;fk,k+1=(fk+fk+1)/2;Δfk,k+1=fk+1-fk;T为待分析信号的长度;α，β，γ为相关参数,文献[9]指出,当α=2，β=4，γ=0.4时,可以完全分离密集模态,充分消除端点效应.

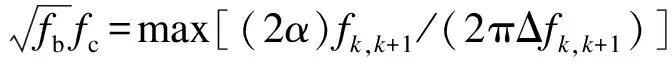
(10)

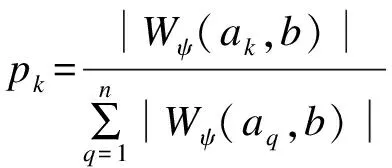
3 苏通大桥主梁振动模态识别

3.1 主梁竖弯模态参数识别

本文以“海葵”台风激励下苏通大桥SHMS系统中振动监测子系统记录的主梁跨中各向加速度响应为分析对象,采用WT方法对主梁各阶模态参数进行识别.选取主梁加速度样本时段为2012年8月8日凌晨00:00—01:00,采样频率为20 Hz,共计72×103个样本点(见图2).采用随机减量技术(RDT)对样本数据进行预处理,子样本取2 048个数据点,水平阀值取为1.5σ(σ为样本数据的标准差),子样本数为468.对样本数据预处理后,得到如图3(a)所示的多分量随机减量信号(MRDS).由图可知,MRDS总体形状与单自由度系统自由衰减曲线类似,但曲线局部并不光滑,这是由于MRDS中存在若干高频分量所导致的.图3(b)为其对应的功率谱密度曲线(PSD).

图2 主梁跨中截面实测加速度响应时程

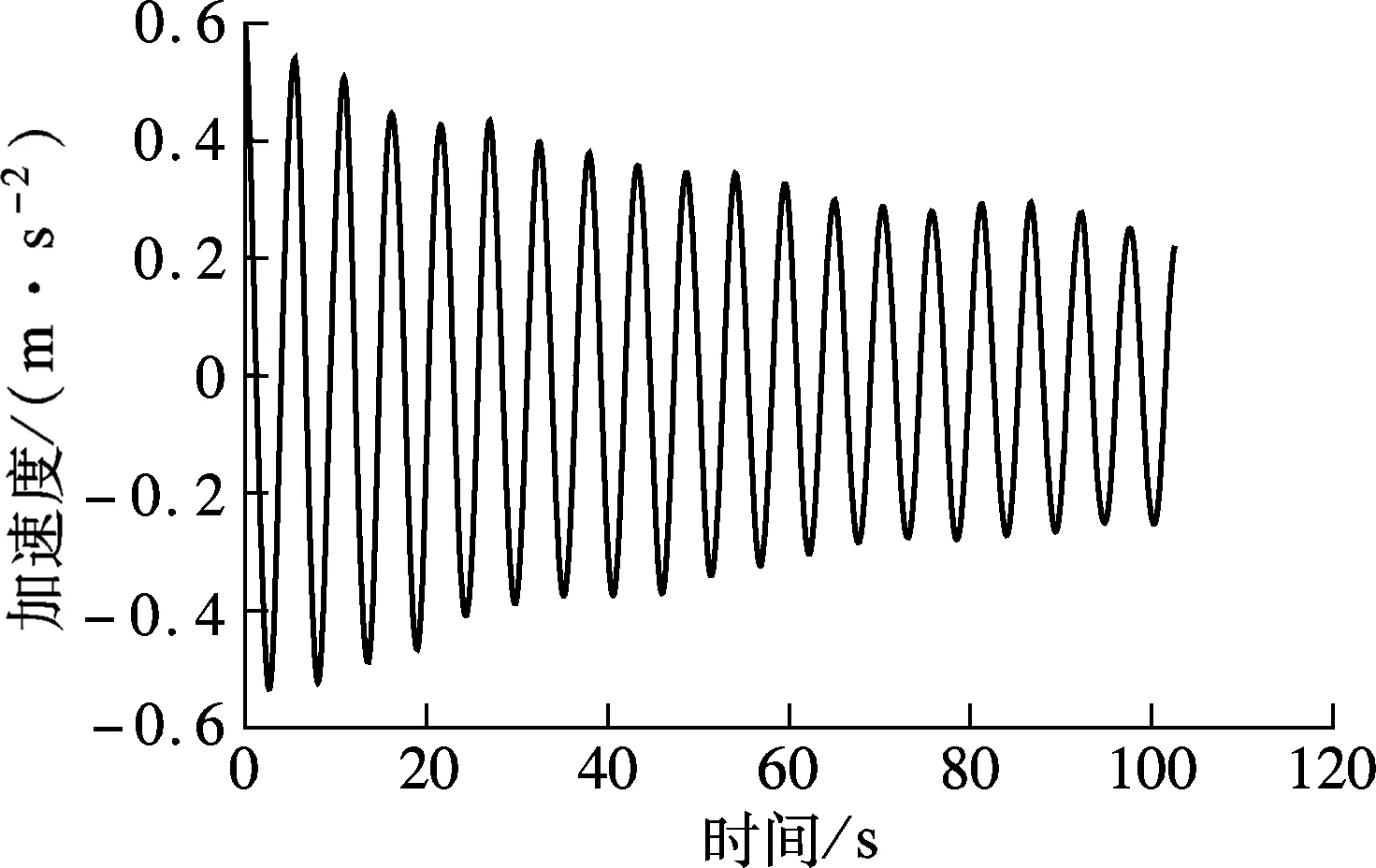
(a) 信号时程曲线

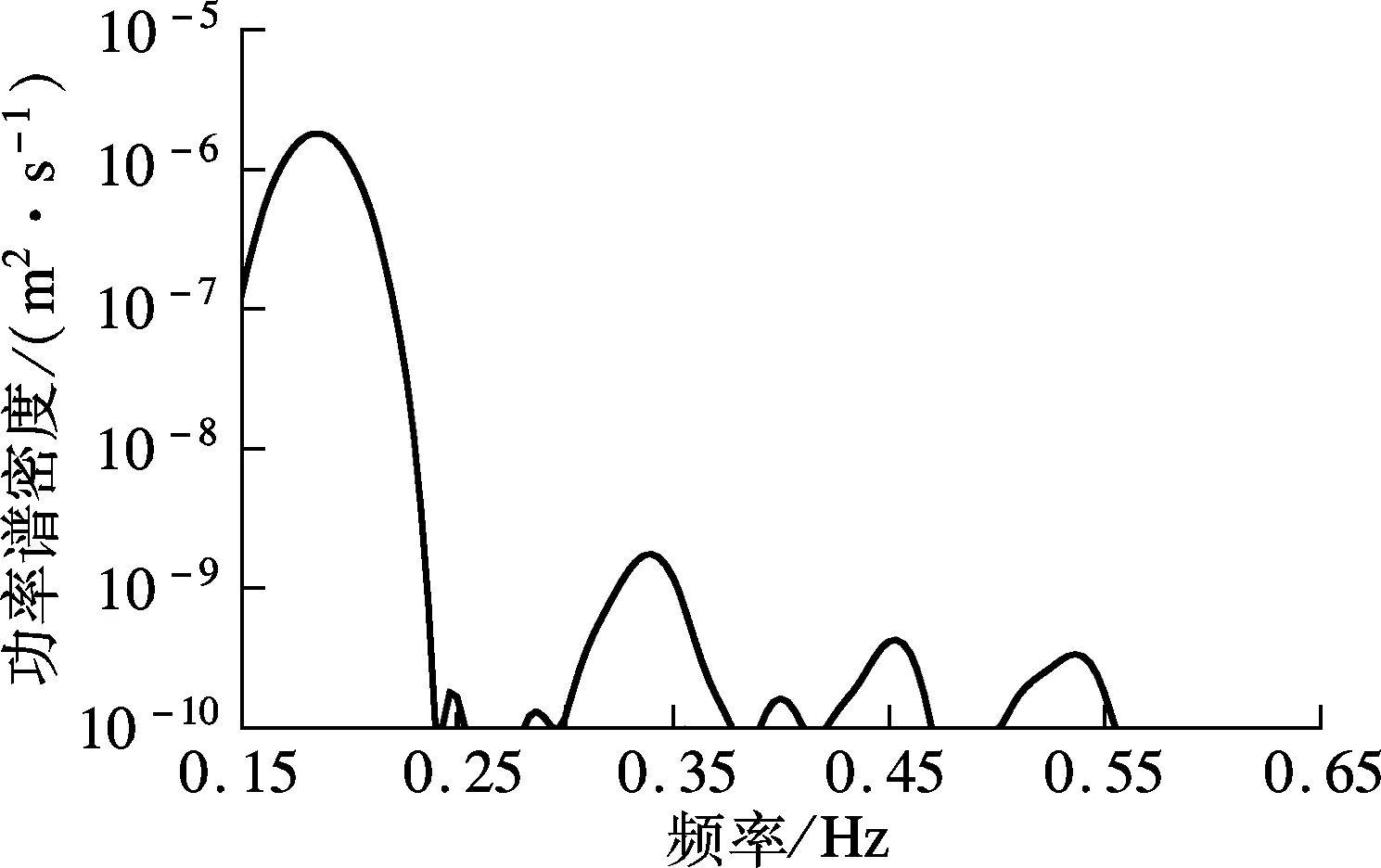
(b) 功率谱密度曲线

由于连续小波变换在低频区存在明显的端点效应,在确保信号分析长度的基础上,对MRDS信号进行对称延拓,各端点处延拓512个数据点.然后,根据式(2)对延拓后的信号进行连续小波变换,并提取原始信号对应的小波系数,其时频分布图如图4所示.根据式(10),确定连续小波变换母小波的相关参数,最优参数选取为fb=8 Hz,fc=4 Hz.由图可知,样本信号的能量主要集中在少数几个频率处,并随着时间的推移呈衰减趋势.

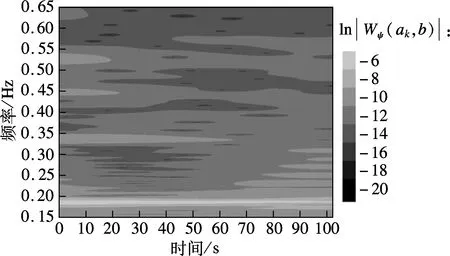
图4 样本信号时频分布量图

为了进一步分析信号的时频分布情况,基于模极大值理论提取了小波系数的小波脊曲线(见图5).由图5可知,前80 s内各阶小波脊对应的频率值较为稳定,随时间变化较小;85 s后小波脊对应的频率值变化较大,这是由于随着时间的增加,MRDS信号高阶分量的能量衰减较大,WT方法对高阶分量的识别精度下降.因此,后续分析中,仅取前51.2 s对应的小波系数进行模态参数识别.

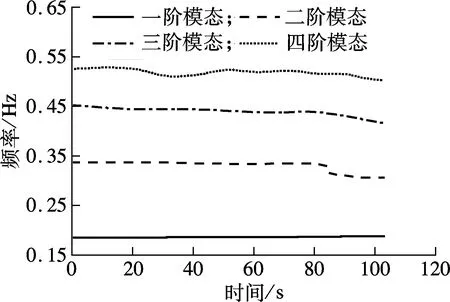
图5 小波系数脊线识别的瞬时频率

图6为主梁前4阶竖向模态对应的小波系数幅值及相位曲线,对其进行最小二乘拟合,并结合式(6)和(7),求得对应的模态频率f及阻尼比ξ.由图可知,各阶模态对应的幅值及相位曲线拟合结果均较好.前4阶模态对应的模态频率分别为0.185 5,0.338 4,0.443 8,0.526 1 Hz,阻尼比分别为0.56%,2.02%,1.45%,1.02%.

3.2 基于WT的模态参数可靠性分析

为了进一步验证WT方法模态参数识别的准确性与可靠性,以2012年8月8日00:00—24:00“海葵”台风激励下的主梁跨中加速度响应为分析对象,取1 h为基本时距,采用WT方法对主梁的竖弯、侧弯及扭转模态参数进行识别,并统计其均值与标准差.在此基础上,将采用WT法识别的结果与文献[11-12]提供的模态参数进行对比,结果见表1.由表1可知,在统计时段内,采用WT方法识别的各阶模态频率与有限元结果均较为吻合,相差最大的一阶扭转模态频率偏差率也仅为1.2%.对模态阻尼比而言,利用WT法识别的结果大都处于文献[12]提供的参考范围内,仅二阶竖弯模态阻尼比略偏大;文献[13]指出,模态阻尼比随温度、风速和车辆等环境因素影响较大,此偏差在正常的波动范围之内.总体而言, WT方法能较好地识别模态频率和模态阻尼比,且具有一定的可靠性.

3.3 千米级斜拉桥模态参数演变特性

国内外研究表明,长时间的实测振动数据往往表现出较强的非平稳性,而在利用RDT对样本信号进行预处理时则要求样本信号具有平稳性.Kijewski[14]指出,将样本信号分段处理成若干短持时子样本是一种较好的解决方法.因此,将样本信号平均分成24段,计算每个基本时距内的模态参数.图7描述了“海葵”台风激励下主梁各阶模态参数的变化情况.

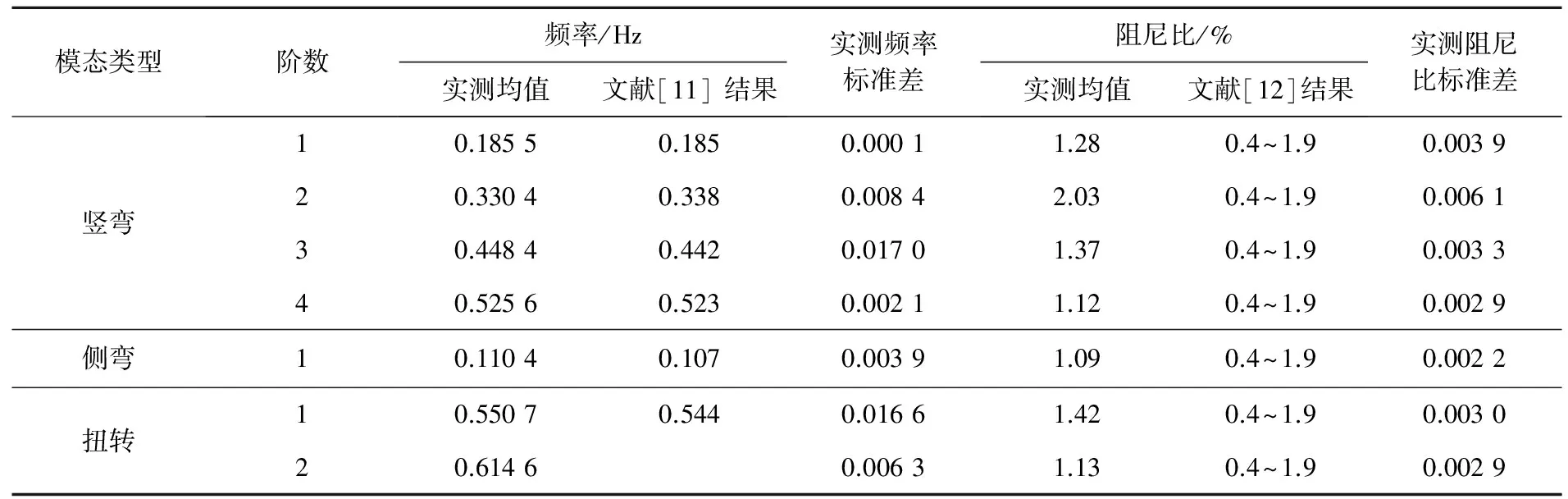
表1 基于WT模态参数识别结果

由表1和图7可知,随着时间的推移,主梁各阶模态频率的波动均较小,其中主梁第1阶竖弯、第4阶竖弯和第1阶侧弯模态频率的波动可以忽略不计,而主梁第1阶扭转模态频率的波动最为明显.在“海葵”台风期间,主梁第2阶竖弯的阻尼比最大,为2.03%;主梁第1阶侧弯的阻尼比最小,为1.09%.随着时间的推移,主梁各阶模态阻尼比的波动均较明显,其中主梁第2阶竖弯阻尼比的波动最为明显,其余各阶振型阻尼比的波动水平相差不大.

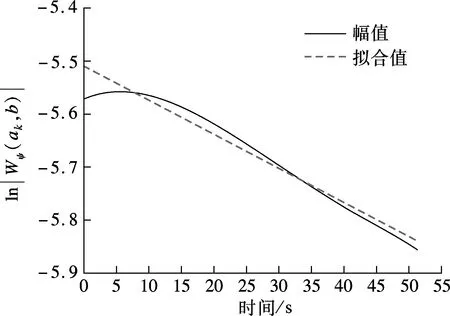
(a) 一阶幅值

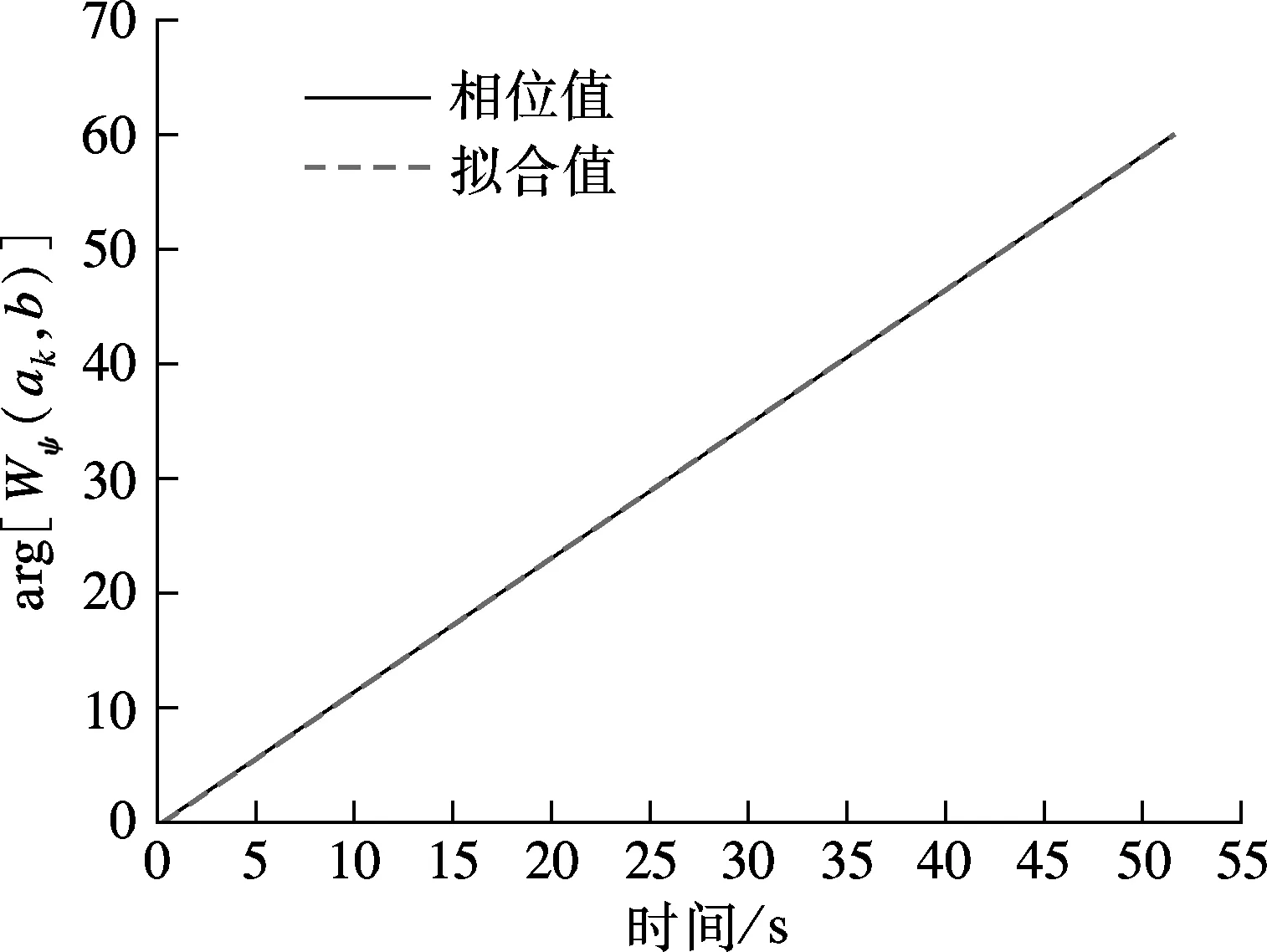
(b) 一阶相位

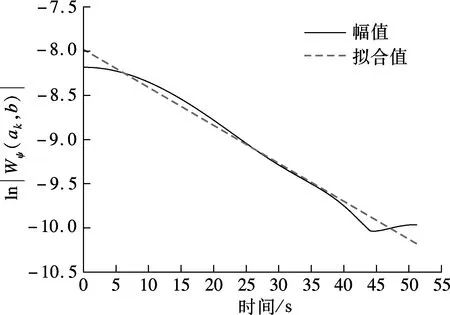
(c) 二阶幅值

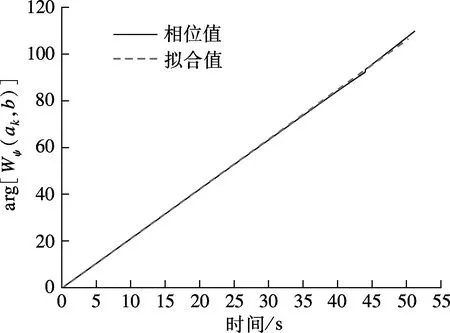
(d) 二阶相位

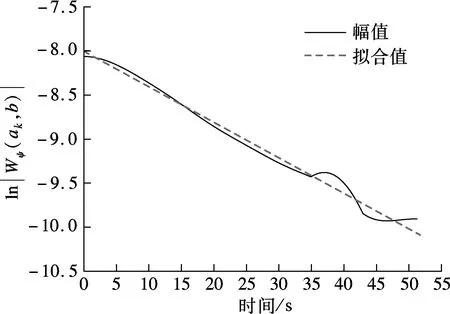
(e) 三阶幅值

(f) 三阶相位

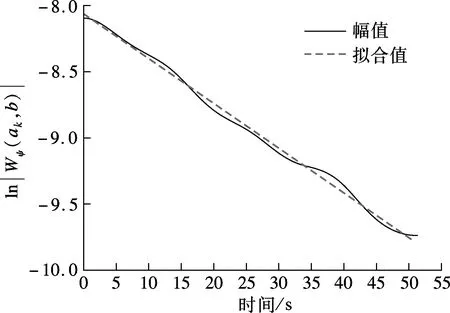
(g) 四阶幅值

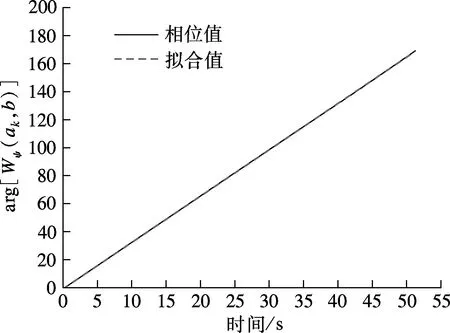
(h) 四阶相位

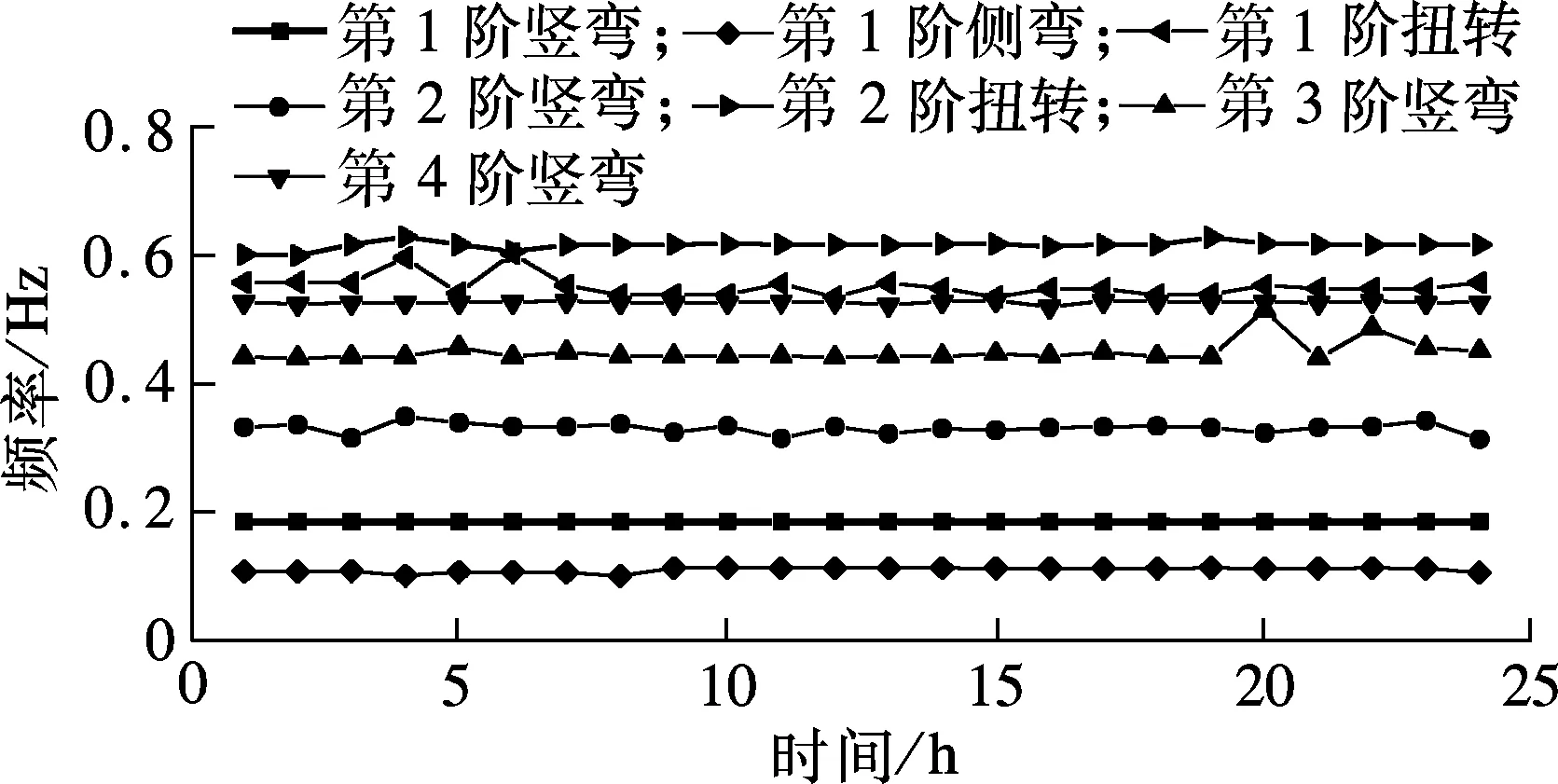
(a) 模态频率

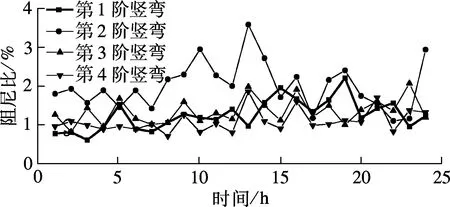
(b) 竖弯模态阻尼比

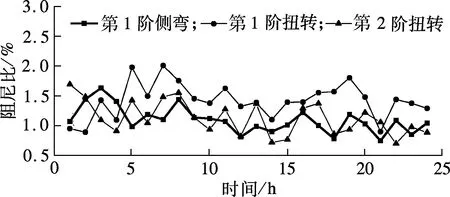
(c) 侧弯及扭转模态阻尼比

4 结论

1) 结合随机减量技术,WT方法可较好地实现对低频密集模态的分离,从而识别出各阶模态对应的频率及阻尼比.竖弯模态低频、密集等特点导致模态参数识别困难,本文通过采用限定MRDS长度、端点对称延拓和选择合理的母小波参数等方法来解决这一问题.对苏通大桥主梁而言,本文共识别出前4阶竖弯、第1阶侧弯及前2阶扭转模态参数.

2) 在统计时段内,利用WT方法识别的模态频率与有限元结果较为吻合;模态阻尼大都处于0.4～1.9之间.总体而言,WT方法能够实现对模态参数的可靠识别.

3) 在“海葵”台风期间,主梁各阶模态频率的波动均较小,而其各阶模态阻尼比的波动则较明显.这表明环境因素包括温度、风速和车辆等对主梁频率影响较小,而对模态阻尼比影响则较大.

References)

[1]Los Alamos National Laboratory. Damage identification and health monitoring of structural and mechanical systems from changes in their vibration characteristics: a literature review [R].Los Alamos,NM,USA:LANL,1996.

[2]秦世强,蒲黔辉,施洲.环境激励下大型桥梁模态参数识别的一种方法[J].振动与冲击,2012,31(2):95-100. Qin Shiqiang,Pu Qianhui,Shi Zhou.A method of modal parameters identification using ambient vibration measurements for a large-scale bridge [J].JournalofVibrationandShock,2012,31(2):95-100.(in Chinese)

[3]辛峻峰, 王树青, 刘福顺. 数据驱动与协方差驱动随机子空间法差异化分析[J]. 振动与冲击, 2013, 32(9): 1-4,20. Xin Junfeng, Wang Shuqing, Liu Fushun. Performance comparison for data-driven and covariance-driven stochastic subspace identification method [J].JournalofVibrationandShock, 2013, 32(9): 1-4,20. (in Chinese)

[4]邓先来. 环境激励下基于小波分析的结构模态参数识别研究[D]. 南京: 南京航天航空大学航空宇航学院, 2011.

[5]Lardies J, Gouttebroze S. Identification of modal parameters using the wavelet transform [J].InternationalJournalofMechanicalSciences, 2002, 44(11): 2263-2283.

[6]Kijewski T, Kareem A. Wavelet transforms for system identification in civil engineering [J].Computer-AidedCivilandInfrastructureEngineering, 2003, 18(5): 339-355.

[7]伊廷华, 李宏男, 王国新. 基于小波变换的结构模态参数识别[J]. 振动工程学报, 2006, 19(1): 51-56. Yi Tinghua, Li Hongnan, Wang Guoxing. Structural modal parameter identification based on wavelet transform [J].JournalofVibrationEngineering, 2006, 19(1): 51-56. (in Chinese)

[8]Sarparast H, Ashory M R, Hajiazizi M, et al. Estimation of modal parameters for structurally damped systems using wavelet transform [J].EuropeanJournalofMechanics—A/Solids, 2014, 47: 82-91.

[9]Yan B, Miyamoto A. A comparative study of modal parameter identification based on wavelet and Hilbert-Huang transforms [J].Computer-AidedCivilandInfrastructureEngineering, 2006, 21(1): 9-23.

[10]Lin J, Qu L S. Feature extraction based on Morlet wavelet and its application for mechanical fault diagnosis [J].JournalofSoundandVibration, 2000, 234(1): 135-148.

[11]王浩, 李爱群, 谢静, 等. 台风作用下超大跨度斜拉桥抖振响应现场实测研究[J]. 土木工程学报, 2010, 43(7): 71-78. Wang Hao, Li Aiqun, Xie Jing, et al. Field measurement of the buffeting response of a super-long-span cable-stayed bridge under typhoon [J].ChinaCivilEngineeringJournal, 2010, 43(7): 71-78. (in Chinese)

[12]张喜刚, 陈艾荣. 苏通大桥设计与结构性能[M]. 北京: 人民交通出版社, 2010: 174-177.

[13]Li H, Li S N, Ou J P, et al. Modal identification of bridges under varying environmental conditions: temperature and wind effects [J].StructuralControlandHealthMonitioring, 2010, 17(5): 495-512.

[14]Kijewski T.Full-scale measurements and system identification:a time-frequency perspective [D].South Bend,Indiana,USA:University of Notre Dame,2003.

Modal parameter identification of kilometer cable-stayed bridge under typhoon excitation based on wavelet transform

Mao Jianxiao Wang Hao Cheng Huaiyu Li Aiqun

(Key Laboratory of Concrete and Prestressed Concrete Structures of Ministry of Education, Southeast University, Nanjing 210096, China)

In order to provide realistic basis for structural damage identification and security evaluation of long span bridges, the modal parameter identification of a kilometer cable-stayed bridge was studied by using the wavelet transform (WT) method. The Sutong Bridge excited by the typhoon Haikui was taken as the research object. Based on the structural vibration responses recorded by the structural health monitoring system (SHMS) of this bridge, the first four vertical, the first two torsional and the first lateral modal parameters, including the frequency and the damping ratio of the girder, were identified by using the WT method. Then, these results were compared with those from some related references. On this basis, the whole process variation of the parameters of the girder during the typhoon Haikui was investigated. The results show that the modal parameter identification based on the WT method is stable and reliable. With the time passing by, the modal frequencies of the girder are stable while the modal ratios fluctuate obviously.

typhoon; Sutong Bridge; wavelet transform; frequency; damping ratio; parameter identification

2014-08-29. 作者简介: 茅建校(1990—)，男，硕士生；王浩(联系人)，男，博士，副研究员，博士生导师，wanghao1980@seu.edu.cn.

国家重点基础研究发展计划(973计划)资助项目(2015CB060000)、国家自然科学基金资助项目(51378111)、霍英东教育基金会高等院校青年教师基金资助项目(142007)、教育部新世纪优秀人才支持计划资助项目(NCET-13-0128)、华南理工大学亚热带建筑科学国家重点实验室开放基金资助项目(2014KA04).

茅建校，王浩,程怀宇，等：基于小波变换的台风激励下千米级斜拉桥模态参数识别[J].东南大学学报:自然科学版,2015,45(1):159-164.

10.3969/j.issn.1001-0505.2015.01.028

U448

A

1001-0505(2015)01-0159-06