交换可剩余半群的剩余BCI-代数

杨 闻 起

(宝鸡文理学院数学与信息科学学院，陕西 宝鸡 721013)

交换可剩余半群的剩余BCI-代数

杨 闻 起

(宝鸡文理学院数学与信息科学学院，陕西 宝鸡 721013)

引入了交换可剩余半群的剩余BCI-代数的概念并讨论了其性质，表明了交换可剩余半群与BCI-代数的关系，得到了全序半群的剩余BCI-代数是BCK-代数，序半群是平凡的当且仅当其剩余BCI-代数是p-半单的.还给出了交换可剩余半群与其剩余BCI-代数的理想和滤子之间的关系.

序半群；交换可剩余半群；BCI-代数；理想；滤子

1 预备知识

序半群是半群结构与序结构相互交融的产物，可剩余半群是一类重要的序半群.文献[1]系统地论述了序半群理论.

定义1[1]设S是半群，“≤”为S上的偏序，∀a，b，c∈S，如果当a≤b时，必有

ac≤bc，ca≤cb，

则称S为序半群，记为(S，≤，·)，在不致混淆时，也简记为S.

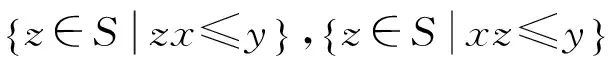
在交换序半群中，左剩余与右剩余等价，故在交换剩余半群中，把左、右剩余统称为剩余.另外，根据本文的需要，把交换半群中的乘法改写为加法，那么有下面的结论.

引理1[1]在交换可剩余半群S中，∀x，y，z∈S，有以下公式成立：

(1) (y∶x)+x≤y，y≤(y+x)∶x，y≤x∶(x∶y)；

(2) (x∶y)∶z=x∶(y+z)，(x∶y)∶z=(x∶z)∶y；

(3) (x∶y)+z≤(x+z)∶y；

(4)a≤b⟹∀x∈S，有a∶x≤b∶x，x∶b≤x∶a.

在交换可剩余半群(S，+，≤)中，如果存在元素0，使得∀x∈S，有0+x=x+0=x，则称0为零元.设m∈S，如果∀x∈S，由m≤x可推出x=m，称m是S中的极大元.

零元是极大元的交换可剩余半群是一类重要的序半群，文献[2-3]从不同的角度研究了它的性质.为叙述方便，本文把零元是极大元的交换可剩余半群记为(S，+，≤，0)，0表示零元，它同时还是一个极大元.

BCI-代数是一类重要的逻辑代数，文献[4]系统地论述了相关理论.

定义3[4]设集合X上有运算*及常元0.∀x，y，z∈X，如果：

(1) ((x*y)*(x*z))*(z*y)=0，

(2)x*0=x，

(3)x*y=0且y*x=0⟹x=y.

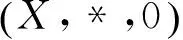
(4) 0*x=0，

则称X是BCK-代数.

在BCI(BCK)-代数X中规定x≤′y⟺x*y=0，那么“≤′”是X上的偏序，叫作X的自然偏序，且0为该偏序的极小元(最小元)，把偏序集(X，≤′)也叫作该BCI(BCK)-代数的自然偏序集.

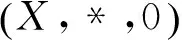
(1)x*x=0；

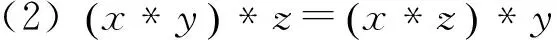
(3)x*(x*y)≤′y；

(4) (x*z)*(y*z)≤′x*y;

(5)x*(x*(x*y))=x*y；

(6) 0*(x*y)=(0*x)*(0*y)；

(7) 由x≤′y可推出x*z≤′y*z，z*y≤′z*x.

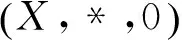
本文试图研究以下三个问题：

(1) 什么样的序半群能导出BCI-代数？

(2) 由序半群导出的BCI-代数有怎样的性质和作用？

(3) 序半群与它导出的BCI-代数的理想和滤子之间的关系如何？

2 交换可剩余半群的剩余BCI-代数

定理1 设(S，+，≤，0)是一个以0为零元的交换可剩余半群，且0为极大元，a∶b表示a关于b的剩余，那么(S，∶，0)是一个以0为零元的BCI-代数.特别地，如果0是最大元，那么(S，∶，0)是一个以0为零元的BCK-代数.

证明 ∀x，y，z∈S，有：

(1) 如果x∶y=0，那么0+y≤x，即y≤x；反之，如果y≤x，0+y≤x，则0≤x∶y，但0为极大元，故x∶y=0.从而x∶y=0当且仅当y≤x，进而x∶y=0，且y∶x=0当且仅当x=y.

(2) 设x∶0=y，由于x+0=x≤x，故x≤y，又因为y=y+0≤x，x=y，从而x∶0=x.

(3) 设x∶y=u，x∶z=v，z∶y=w，则

u+y=y+u≤x，v+z=z+v≤x，w+y=y+w≤z，

故v+w+y≤v+z≤x，w+v=v+w≤x∶y=u，w≤u∶v，由(1)知(u∶v)∶w=0，即((x∶y)∶(x∶z))∶(z∶y)=0.

由定义3知，(X，∶，0)是一个以0为零元的BCI-代数.由于0为零元，0+x=x，如果0还是最大元，即∀x∈S，x≤0，0+x≤0，故0≤0：x，但0是最大元，从而0∶x=0，所以(S，∶，0)是一个BCK-代数.

定义4 在序半群(S，+，≤，0)中，把按照剩余运算“∶”做成的BCI-代数(S，∶，0)叫作该序半群的剩余BCI-代数.特别地，如果0是最大元，把BCK-代数(S，∶，0)叫作该序半群的剩余BCK-代数.

必须注意，由于BCI-代数(S，∶，0)的自然偏序为x≤′y⟺x∶y=0，而由定理1的证明过程知，序半群(S，+，≤，0)的偏序为x≤y⟺y∶x=0，可见，这两个偏序互相对偶，从而序半群的极大元就是其剩余BCI-代数的极小元.另外，我们还可以把定义3和引理2中的公式直接转化为序半群(S，+，≤，0)关于剩余运算的公式.

引理3 在序半群(S，+，≤，0)中，∀x，y，z∈S，有以下公式成立：

(1)x∶y=0⟺y≤x，x=y⟺x∶y=y∶x=0；

(2)x∶0=x；

(3)z∶y≤(x∶y)∶(x∶z)；

(4) 0∶(x∶y)=(0∶x)∶(0∶y)；

(5)x∶x=0；

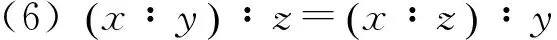
(7) (x∶z)∶(y∶z)≥x∶y；

(8)x∶(x∶(x∶y))=x∶y；

(9) 0∶(x∶y)=(0∶x)∶(0∶y)；

(10) 由x≤y可以推出x∶z≤y∶z，z∶y≤z∶x.

定理2 全序半群(S，+，≤，0)的剩余BCI-代数(S，∶，0)是BCK-代数.

证明 设序半群(S，+，≤，0)是全序的，由于0是极大元，这时0必为最大元，从而在剩余BCI-代数(S，∶，0)中0就是最小元，由定理1知(S，∶，0)是BCK-代数.

在半群S中，如果取偏序为∀x，y∈S，x≤y⟺x=y，称该序半群是平凡的.

显然，以下命题等价：(1)序半群S是平凡的；(2)每个元素都是极大元；(3)任意两个不同的元素不可比较；(4)偏序≤与其反序≥保持一致.

定理3 序半群(S，+，≤，0)是平凡的当且仅当它的剩余BCI-代数(S，∶，0)是p-半单的.

证明 设序半群(S，+，≤，0)是平凡的，即每个元素都是极大元，从而它的剩余BCI-代数(S，∶，0)中的每个元素都是极小元，从而它的剩余BCI-代数(S，∶，0)是p-半单的.由于以上各步都可逆，故反过来也成立.

定理4 设序半群(S，+，≤，0)的剩余BCI-代数为(S，∶，0)，则BCI-代数(S，∶，0)的加法序半群是(S，+，≤，0)，当且仅当序半群(S，+，≤，0)是平凡的.

证明 设BCI-代数为(S，∶，0)的加法序半群为(S，+′，≤′，0)，如果序半群(S，+，≤，0)是平凡的，则偏序≤的反序还是自身，即加法序半群的偏序≤′就是≤.另外，∀x，y∈S，由引理1，x+′y=0∶((0∶x)∶y)=0∶(0∶(x+y))，但由定理3知，BCI-代数(S，∶，0)是p-半单的，故0∶(0∶(x+y))=x+y，从而x+′y=x+y，即两个加法运算一致，从而BCI-代数(S，∶，0)的加法序半群就是序半群(S，+，≤，0).反过来，如果BCI-代数为(S，∶，0)的加法序半群就是原序半群(S，+，≤，0)，则偏序≤的反序还是≤，故序半群(S，+，≤，0)是平凡的.

我们知道，全序与平凡偏序是偏序的两个极端，而BCK-代数与p-半单BCI-代数也是BCI-代数的两个极端，定理2和定理3表明，这两个极端的序半群恰好导出这两个极端的BCI-代数.

3 交换可剩余半群与其剩余BCI-代数的理想和滤子

文献[1]给出了序半群的理想和滤子的概念：设S是序半群，A是S的非空子集.如果：(1)a∈A，s∈S⟹as，sa∈A；(2)b≤a∈A⟹b∈A.则称A是S的理想.如果：(1)ab∈A⟺a，b∈A；(2)b∈A，b≤a⟹a∈A.则称A是S的滤子.

交换可剩余半群与其剩余BCI-代数的理想和滤子有着紧密的联系.

定理5 设A是序半群(S，+，≤，0)的滤子，则A必是其剩余BCI-代数(S，∶，0)的理想.

证明 首先，取a∈A，由于0为零元，0+a∈A.注意到A是序半群(S，+，≤，0)的滤子，故0∈A.其次，设a∈A，b∶a∈A，则(b∶a)+a∈A，由引理1知(b∶a)+a≤b，故b∈A，从而A必是BCI-代数(S，∶，0)的理想.

定理6 如果A是序半群(S，+，≤，0)的理想，且A关于剩余运算“∶”封闭，那么A必是其剩余BCI-代数(S，∶，0)的滤子.

证明 任取a∈A，由于A关于剩余运算“∶”封闭，故0=a∶a∈A.再设a∶b∈A，由引理1知，b≤a∶(a∶b)∈A，且A是序半群(S，+，≤，0)的理想，故b∈A，所以A是BCI-代数(S，∶，0)的理想.

引理4[4]用M(S)表示BCI-代数(S，*，0)的全部极小元，则M(S)={0*x|x∈S}.

定理7 设序半群(S，+，≤，0)的剩余BCI-代数为(S，∶，0)，M(S)⊆A⊆S，如果A是BCI-代数为(S，∶，0)的理想，那么A必是序半群(S，+，≤，0)的滤子.

证明 设A是BCI-代数为(S，∶，0)的理想.首先，∀a，b∈A，由引理1和定理3知((a+b)∶a)∶b=(a+b)∶(a+b)=0∈A，由于A是BCI-代数的理想，且a，b∈A，故a+b∈A.反过来，设a+b∈A，由引理1和引理3知a∶(a+b)=(a∶a)∶b=0∶b.由引理4知，0∶b是BCI-代数中的极小元.从而0∶b∈A，即a∶(a+b)∈A，由于a+b∈A，且A是BCI-代数为(S，∶，0)的理想，故a∈A，同理也有b∈A.

其次，设a∈A，a≤b，则b∶a=0∈A，但A是BCI-代数的理想，故b∈A，从而A必是序半群(S，+，≤，0)的滤子.

定理8 设序半群(S，+，≤，0)的剩余BCI-代数为(S，∶，0)，M(S)⊆A⊆S，如果A是BCI-代数(S，∶，0)的滤子，那么A必是序半群(S，+，≤，0)的理想.

证明 设A是BCI-代数为(S，∶，0)的滤子.∀a∈A，∀s∈S，由引理1和引理3知，a∶(a+s)=(a∶a)∶s=0∶s.由引理4知0∶s是BCI-代数的极小元，故0∶s∈A，从而a∶(a+s)∈A，但a∈A，且A为BCI-代数的滤子，故s+a=a+s∈A.

其次，设b≤a∈A，则a∶b=0∈A，但A为BCI-代数为(S，∶，0)的滤子，故b∈A.所以A是序半群(S，+，≤，0)的理想.

[1] 谢祥云.序半群引论[M].北京：科学出版社，2001：5-19.

[2] 李继成.剩余幺半群的商结构[J].纯粹数学与应用数学，1995，11(1)：109-113.

[3] 李继成.关于剩余幺半群中元素的剩余周期[J].陕西师范大学学报(自然科学版)，1995，23(2)：27-30.

[4] HUANG YISHENG.BCI-algebra[M].Beijing：Science Press，2006：11-78.

[5] 杨闻起.BCI-代数与半群[M].北京：科学出版社，2011：87-90.

[6] 杨闻起.IS-代数的伴随半环[J].东北师大学报(自然科学版)，2012，44(3)：46-51.

[7] 杨闻起.强序半群的伴随KS-代数[J].东北师大学报(自然科学版)，2014，46(3)：34-37.

[8] 杨闻起.BCI-代数的滤子[J].安徽大学学报(自然科学版)，2013，37(2)：15-18.

(责任编辑：李亚军)

Residual BCI-algebras of the commutative residuated semigroups

YANG Wen-qi

(College of Mathematics and Informatics，Baoji University of Arts and Sciences，Baoji 721013，China)

The concept of the residual BCI-algebra of a commutative residuated semigroup is introduced and the relation between them are discussed.In addition，two conclusions are obtained as follows. One is that the residual BCI-algebra of a total semigroup is a BCK-algebra.The other is that a ordered semigroup is trivial if and only if its residual BCI-algebra is p-semisimple.Besides，the relation of its ideal and filter between the residual BCI-algebra and a commutative residuated semigroup are investigated.

ordered semigroup;commutation residuated semigroup；BCI-algebra；ideal;filter

1000-1832(2015)04-0022-04

10.16163/j.cnki.22-1123/n.2015.04.005

2014-05-05

陕西省自然科学基金资助项目(2010JM1016)；陕西省教育厅专项基金资助项目(14JK1050).

杨闻起(1962—)，男，教授，主要从事代数学研究.

O 153.1 [学科代码] 110·2115

A