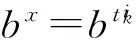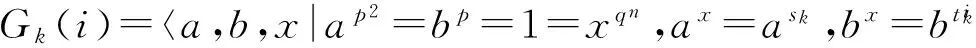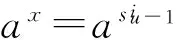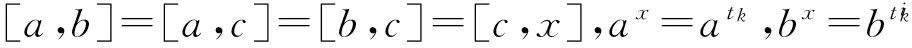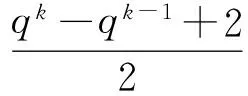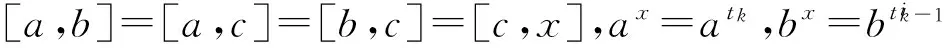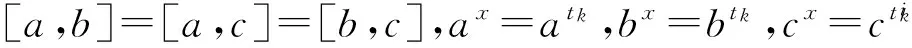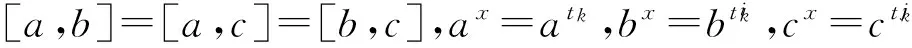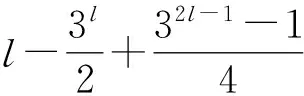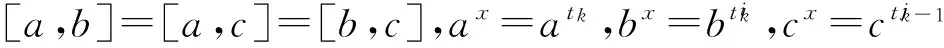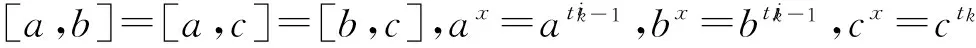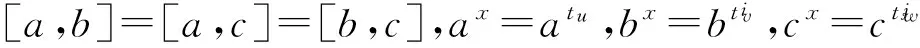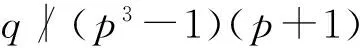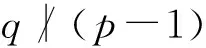Sylow q-子群循环的p3qn阶群的分类

陈 松 良

(贵州师范学院数学与计算机科学学院，贵州 贵阳 550018)

Sylowq-子群循环的p3qn阶群的分类

陈 松 良

(贵州师范学院数学与计算机科学学院，贵州 贵阳 550018)

设p，q是两个奇素数，且p>q，n是正整数，G是Sylowq-子群循环的p3qn阶群，对G进行了同构分类，并确定了Sylowq-子群循环的p3qn阶群的全部构造.

有限群；同构分类；群的构造

设p，q是不同的素数，文献[1]对p3q阶群进行了分类，文献[2]研究了23p阶群(p是奇素数)，得到了其全部构造.对于任意正整数n，p3qn阶群的构造是非常复杂的，但当p>q时，文献[3]确定了Sylowp-子群循环的pnq3阶群的全部构造，这是对文献[1]的一种推广.本文将继续推进这一工作，确定Sylowq-子群循环的p3qn阶群的全部构造.

1 主要结果

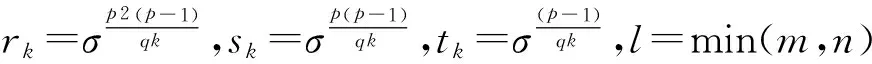
定理1 设G是Sylowq-子群循环的p3qn阶群，那么：

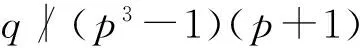
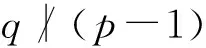
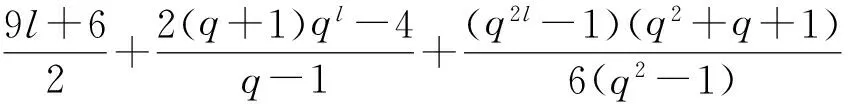
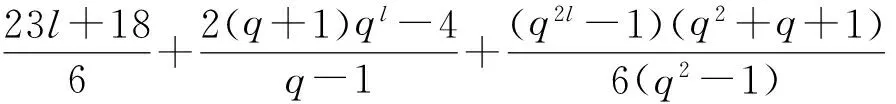
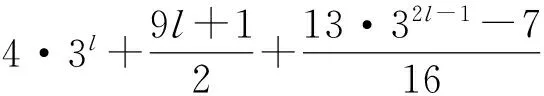
(6) 当qm‖(p+1)，且m≥1时，G恰有5+2l个不同构的类型.

2 定理证明

设G是Sylowq-子群循环的p3qn阶群，P是G的一个Sylowp-子群，Q是G的一个Sylowq-子群，则可设Q的构造是Q=〈x〉，其中|x|=qn.而由文献[2]之定理7.1，P必为下列5种类型之一：

(ⅰ)P1=〈a|ap3=1〉；

(ⅲ)P2=〈a，b|ap2=bp=1=[a，b]〉；

(ⅳ)P3=〈a，b，c|ap=bp=cp=1=[a，b]=[a，c]=[b，c]〉；

(ⅳ)P4=〈a，b|ap2=1=bp，ab=ap+1〉；

(ⅴ)P5=〈a，b，c|ap=bp=cp=1=[a，c]=[b，c]，[a，b]=c〉.

由于p>q，所以由文献[4]之定理Ⅳ.2.8得，P◁G，从而G=PQ.因此，我们作如下讨论.

2.1 P≅P1时G的构造

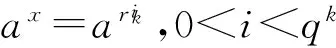
Gk=〈a，x|ap3=1=xqn，ax=ark〉.

(1)

引理1 如果G是Sylow子群皆循环的p3qn阶群，那么当qm‖(p-1)时，G恰有1+l个互不同构的形如(1)式的构造.

2.2 P≅P2时G的构造

由于P的Frattini子群Φ(P)=〈ap〉是p阶群，而Φ(P)charP，P◁G，于是Φ(P)◁G.又〈ap，b〉是P唯一的p2阶初等交换子群，从而它是P的特征子群，于是它又必是G的正规子群.故G是超可解群.

由于〈ap〉及〈ap，b〉均为G的正规子群，从而都是Q-不变的.由文献[8]之定理8.4.6知，〈ap〉在〈ap，b〉中有Q-不变的补子群，不失一般性，可设〈b〉是Q-不变的.于是〈ap，b〉/〈ap〉是Q-不变的p2阶初等交换p-群〈a，b〉/〈ap〉的Q-不变子群，因此再由文献[8]之定理8.4.6知，〈ap，b〉/〈ap〉在〈a，b〉/〈ap〉中有Q-不变的p阶补子群〈aibj〉/〈ap〉，其中，0

(1)当k≥u的情形

(2)

(2)当k

(3)

2.3 P≅P3时G的构造

P的自同构群Aut(P)的阶是(p3-1)(p3-p)(p3-p2).当q不整除(p3-1)(p+1)时，Q在P上的作用只能是平凡的，从而G是交换群，其构造

G=〈a，b，c，x|ap=bp=cp=xqn=1=

[a，b]=[a，c]=[a，x]=[b，c]=[b，x]=[c，x]〉.

(4)

当q整除(p3-1)(p+1)时，G也可以是非交换群.由文献[8]之定理8.4.2，P=CP(Q)×[P，Q].

(1) 如果CP(Q)是p2阶群，则不妨设CP(Q)=〈b，c〉，[P，Q]=〈a〉，这时应有q整除(p-1)，从而类似于2.1，G有构造

Gk=〈a，b，c，x|ap=bp=cp=xqn=1=

[a，b]=[a，c]=[b，c]=[b，x]=[c，x]，ax=atk〉.

(5)

其中1≤k≤l，qm‖(p-1)，m≥1.易见构造(5)共表示l个互不同构的p3qn阶群.

(2) 如果CP(Q)是p阶群，则不妨设CP(Q)=〈c〉，[P，Q]=〈a，b〉，于是Q无不动点的作用在〈a，b〉上.

(a) 首先，假定Q〈a，b〉是超可解群，于是不妨假设〈a〉，〈b〉都是Q-不变的，从而必有q整除(p-1)，且CQ(a)与CQ(b)都不是Q.

(ⅰ) 当CQ(a)=CQ(b)时，G可有构造

Gk(i)=〈a，b，c，x|ap=bp=cp=xqn=1=

(6)

(ⅱ) 当CQ(a)≠CQ(b)时，应有qm‖(p-1)，m≥2，不妨假设CQ(a)

Gk(i)=〈a，b，c，x|ap=bp=cp=xqn=1=

(7)

(b) 其次，假定Q〈a，b〉不是超可解群，那么Q在〈a，b〉上的作用是不可约的.又〈a，b〉是p-元域p上的2维线性空间，x是它的1个可逆线性变换，于是x的特征多项式(记为f(λ))是p上的2次不可约多项式，但x是q-元，所以存在正整数k，使得f(λ)整除λqk-1.另一方面，p上的全体2次不可约多项式的积是(λp2-1-1)/(λp-1-1)，因此q整除(p+1).设x的矩阵是M，则|M|qk≡1(modp).又显然(q，p-1)=1，且|M|p-1≡1(modp)，所以|M|≡1(modp).当qm‖(p+1)，m≥1，x是〈a，b〉的qk阶线性变换时，1≤k≤l，可设f(λ)=λ2-βkλ+1，它是(λqk-1)/(λqk-1-1)的2次不可约因式，于是G有构造

Gk=〈a，b，c，x|ap=bp=cp=xqn=1=

[a，b]=[a，c]=[b，c]=[c，x]，ax=b，bx=a-1bβk〉.

(8)

其中1≤k≤l，而qm‖(p+1)，m≥1，βk∈p，使得λ2-βkλ+1是p元域p上多项式(λqk-1)/(λqk-1-1)的一个2次不可约因式.易见构造(8)共代表l个互不同构的p3qn阶群.

(3) 如果CP(Q)=1，且G是超可解群，则不妨设G有正规群列G▷〈a，b，c〉▷〈b，c〉▷〈c〉.显然有q整除(p-1)，由Maschke定理[8]知Q在P上的作用是完全可约的，所以不妨假定〈a〉与〈b〉都是Q-不变的.设qm‖(p-1)，则m≥1.

(ⅰ) 当ax，bx，cx的指数至少有两个相同时，不妨设ax，bx的指数相同，则G有构造

Gk(i)=〈a，b，c，x|ap=bp=cp=xqn=1=

(9)

其中1≤k≤l，0

(ⅱ) 当ax，bx，cx的指数两两不等时(这时，若q=3，则k>1)，则G有构造

Gk(i，j)=〈a，b，c，x|ap=bp=cp=xqn=1=

(10)

其中1≤k≤l，11.因此，集合{i，j}={u，ju}={v，iv}时，必有j3≡1(modqk)，i≡j2(modqk)，且q≡1(mod 3)，或q=3但k>1，同时λ3-1=(λ-1)(λ-i)(λ-j)(modqk).否则集合{i，j}，{u，ju}，{v，iv}是三个不同的集合.反之，若q≡1(mod 3)，或q=3但k>1.则存在唯一的j∈，使得λ3-1=(λ-1)(λ-i)(λ-j)(modqk).从而{i，j}，{u，ju}，{v，iv}是同一个集合当且仅当j3≡1(modqk)，i≡j2(modqk)，而j∈{1}.综上所述，对每个k，当q≡1(mod 3)或q=3但k>1时，构造(10)代表个互不同构的p3qn阶群；当q≡-1(mod 3)时，构造(10)代表个互不同构的p3qn阶群.因此，若qm‖(p-1)，且m≥1，则：

(b) 如果CQ(a)，CQ(b)，CQ(c)中恰有两个相同(这时必有m≥2)，不妨设CQ(a)=CQ(b).

(ⅰ) 当CQ(a)=CQ(b)

Gk(i，j)=〈a，b，c，x|ap=bp=cp=xqn=1=

(11)

(ⅱ) 当CQ(a)=CQ(b)>CQ(c)时，设CQ(c)=〈xqk〉，则G有构造

Gk(i，j)=〈a，b，c，x|ap=bp=cp=xqn=1=

(12)

(c) 如果CQ(a)，CQ(b)，CQ(c)两两不同(这时必有m≥3)，则不妨设CQ(a)=〈xqu〉，CQ(b)=〈xqv〉，CQ(c)=〈xqw〉，其中1≤w

Guvw(i，j)=〈a，b，c，x|ap=bp=cp=xqn=1=

(13)

个互不同构的p3qn阶群.

(4) 如果CP(Q)=1，且G不是超可解群，则Q在P上的作用是不可约的.又x可以看成p元域p上的3阶矩阵，而x没有非平凡不变子空间，于是x的特征多项式f(λ)是p元域p上的3次不可约多项式.又存在正整数m，使得CQ(P)=〈xqm〉，1≤m≤n，此时易知〈xqm〉◁G，而且G/〈xqm〉是补为Q/〈xqm〉而核为P的p3qm阶Frobenius群，于是(qm，p3-1)=qm，即p3≡1(modqm).显然λqm-1是x的矩阵M的零化多项式，所以f(λ)是λqm-1的因式.众所周知，λp3-λ是p上的所有一次不可约多项式和三次不可约多项式的积，于是f(λ)也是λp3-1-1的因式.

Gk=〈a，b，c，x|ap=bp=cp=xqn=1=[a，b]=[a，c]=[b，c]，ax=b，bx=c，cx=abβkcγk〉.

(14)

其中1≤k≤l，q≡1(mod 3)，q|(p-1)，而qm‖(p2+p+1)，m≥1，βk，γk∈p.使得λ3-γkλ2-βkλ-1是p上多项式(λqk-1)/(λqk-1-1)的一个3次不可约因式.

(b) 如果q|(p-1)，则因f(λ)是λqm-1的3次不可约因式，所以也有q|(p2+p+1)，从而q|(p2+p+1，p-1)=(p2+2p，p-1)=(p+2，p-1)=(3，p-1)，因此q=3.由此不难证明3‖(p2+p+1)，于是3m-1‖(p-1)，λ3m-1-1是3m-1个不同的一次因式的积.再由CQ(P)=〈xqm〉知，必有m≥2，且x在P上的作用是P的3m阶自同构，因而f(λ)是p上多项式的一个3次不可约因式.由于σ是p的一个原根，令，则λ3-ζ是p上的一个3次不可约因式.不难验证λ3-ζ的友矩阵是GL(3，p)中的3m阶元，所以λ3-ζ是的一个3次不可约因式，由此可得G的构造

G=〈a，b，c，x|ap=bp=cp=x3n=1=[a，b]=[a，c]=[b，c]，ax=b，bx=c，cx=a-ζ〉.

(15)

综上所述，注意到m=1时，(7)，(10)，(12)式都表示0个G的构造，而m=1，2时，(13)式也表示0个G的构造，因此我们有下面的引理.

引理3 如果G是Sylowq-子群循环而Sylowp-子群为初等交换群的p3qn阶群，那么：

(6) 当qm‖(p+1)，且m≥1时，G恰有1+l个不同构的类型.

2.4 P≅P4时G的构造

不难证明Φ(P)=Z(P)=〈ap〉，而〈ap，b〉是P的唯一的p2阶初等交换子群，从而它们都是G的正规子群，于是G必是超可解群.既然〈ap〉及〈ap，b〉都是Q-不变的，且〈ap，b〉是p2阶初等交换p-群，因此〈ap〉在〈ap，b〉中有Q-不变的补子群，不失一般性，可设〈b〉是Q-不变的.于是〈ap，b〉/〈ap〉是Q-不变的p2阶初等交换p-群〈a，b〉/〈ap〉的p阶Q-不变子群，因此必有某个〈aibj〉/〈ap〉(这里(i，p)=1)是Q-不变的.但aibj与a在Q中的地位是相同的，从而不妨设〈a〉是Q-不变的，于是Q/CQ(a)同构于Aut(〈a〉)的一个子群.当qm‖(p-1)时，设CQ(a)=〈xqk〉，0≤k≤l，于是不妨设ax=ask.另一方面，因〈b〉是Q-不变的，可设bx=btu，0≤u≤l.但[a，b]=ap，于是[ax，bx]=apx=apsk，即apsktu=apsk，所以tu≡1(modp)，bx=b.因此得到G的构造

Gk=〈a，b，x|ap2=bp=xqn=1=[b，x]，ab=a1+p，ax=ask〉.

(16)

其中0≤k≤l，qm‖(p-1).由此有下面的结论.

引理4 如果G是Sylowq-子群循环，而Sylowp-子群为(p2，p)型非交换群的p3qn阶群，那么当qm‖(p-1)时，G恰有1+l个互不同构的类型，其构造形如(16)式.

2.5 P≅P5时G的构造

这时Φ(P)=Z(P)=〈c〉，于是〈c〉◁G，从而P/〈c〉是Q-不变的p2阶初等交换p-群.如果G是超可解的，则G/〈c〉也是超可解的，不妨设〈b，c〉/〈c〉与〈a，c〉/〈c〉是Q-不变的.现在〈b，c〉是Q-不变的初等交换p-群，且〈c〉是Q-不变的，于是〈c〉在〈b，c〉中有Q-不变的补子群，设是〈b〉.同理，可设〈a〉也是Q-不变的.由a，b的对称性，不妨设CQ(a)≤CQ(b).所以当qm‖(p-1)时，可得到G的构造

Gk(i)=〈a，b，c，x|ap=bp=cp=xqn=1=[a，c]=[b，c]，

(17)

如果G不是超可解的，则G/〈c〉是非超可解的.类似于构造(8)的讨论，可知q整除p+1，从而Q〈c〉是交换群，G有构造

Gk=〈a，b，c，x|ap=bp=cp=xqn=1=[a，c]=[b，c]=[c，x]，ab=ac，ax=b，bx=a-1bβk〉.

(18)

其中1≤k≤l，qm‖(p+1)，m≥1，βk∈p，使得λ2-βkλ+1是p元域p上多项式(λqk-1)/(λqk-1-1)的一个2次不可约因式.易见构造(18)共代表l个互不同构的p3qn阶群.综上所述，我们有下面的结论.

由引理1—5可知定理1成立.

[1] WESTERN.Groups of orderp3q[J].Proc L M S，1899，30：209-263.

[2] 张远达.有限群构造[M].北京：科学出版社，1982：687-713，467.

[3] 陈松良.论Sylowp-子群循环的pnq3阶群的构造[J].东北师大学报(自然科学版)，2013，45(2)：35-38.

[4] HUPPERT B.Endliche gruppenI[M].Berlin： Springer-Verlag，1967：329-362.

[5] ALPERIN J L，BELL R B.Groups and representations[M].Beijing： World Publishing Corporation，1997：63-99.

[6] NATHANSON M B.Elementary methods in number theory[M].Beijing： World Publishing Corporation，2003：93.

[7] DOERK K，HAWKES T.Finite soluble groups[M].Berlin，New York：Walter de Gruyter，1992：314-330.

[8] KURZWEIL H，STELLMACHER B. The theory of finite groups[M].New York：Springer-Verlag，2004：183-201.

(责任编辑：李亚军)

On the classification of the groups of orderp3qnwith cylic Sylowq-subgroups

CHEN Song-liang

(School of Mathematics and Computer Science，Guizhou Normal College，Guiyang 550018，China)

Letp，qbe odd primes such thatp>q，andGbe finite groups of orderp3qnwith cyclic Sylowq-subgroups.In this paper，it is discussed that the isomorphic classification ofG，and their structures are completely described.

finite group；isomorphic classification；structure of group

1000-1832(2015)04-0011-07

10.16163/j.cnki.22-1123/n.2015.04.003

2014-01-26

贵州省自然科学基金资助项目(黔科合J字[2012]2289号，[2013]2234号).

陈松良(1964—)，男，博士，教授，主要从事有限群论及应用研究.

O 152.1 [学科代码] 110·2115

A