斜拉桥纵向位移与温度的相关性分析

陈 辉，彭家意

（1.南京长江第二大桥有限责任公司，江苏 南京 210038；2.苏交科集团股份有限公司，江苏 南京 210017）

1 概述

大型桥梁的设计寿命一般是100年［1］，而桥梁伸缩缝的设计寿命一般只有40年而且往往远不到40年伸缩缝就已经损坏，因此伸缩缝是桥梁结构中十分容易损坏的构件，而且也是十分难以修缮的构件［2］。伸缩缝的作用是调节梁端的纵向位移，因此了解梁端纵向位移的变化形态，对伸缩缝的安全评估与养护维修具有一定的指导作用。

不少学者对桥梁的梁端纵向位移进行了研究［3］，他们大都基于健康监测实测数据，提出大跨索承桥梁伸缩缝状态分析与评定方法。有学者对江阴大桥安装纵向阻尼器后的梁端纵向位移进行了详细研究［4］，并针对江阴大桥梁端纵向位移，提出其状态分析与评定方法。这些伸缩缝状态分析与评定方法已经考虑到温度变化的影响，但他们只对悬索桥的梁端纵向位移与温度关系进行了研究，并且证明了这一关系是线性的，而未对斜拉桥梁端纵向位移与主梁有效温度之间的相关性进行分析。

本文依托南京长江第二大桥及其健康监测系统，对其梁端纵向位移与主梁的有效温度［5］进行了分析，从线性和非线性这两个角度研究梁端纵向位移与温度的关系。

2 工程概况

南京长江第二大桥是南京市过境高速公路上的主要桥梁之一［6］，位于南京长江大桥下游11 km处的新生圩附近。南京长江第二大桥是主跨为628 m的双塔双索面5孔连续钢箱梁斜拉桥，建有健康监测系统，其中安装了4个梁端纵向位移传感器位于伸缩缝两侧的上下游，具体布置图如图1所示。

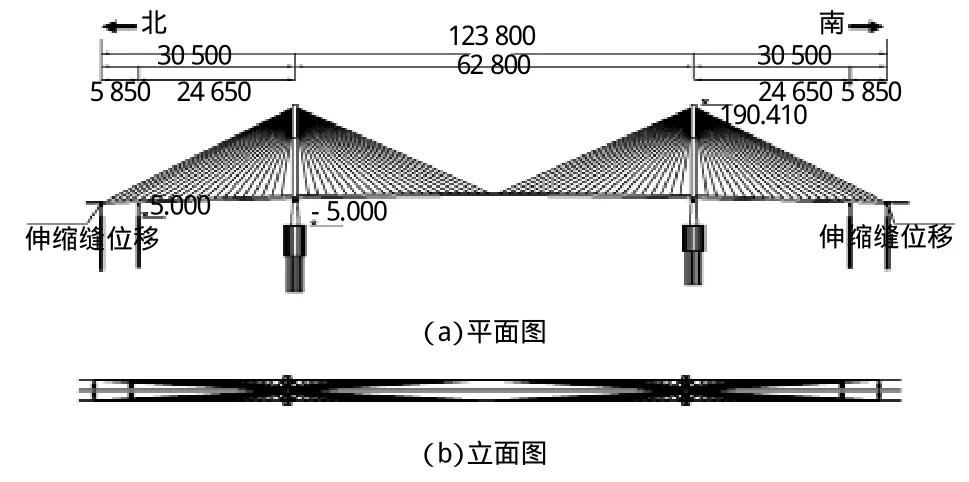
图1 南京长江第二大桥梁端纵向位移传感器布置图

3 梁端纵向位移与温度的相关性分析

梁端纵向位移主要受到温度变化、车辆和风荷载的影响，如下式所示：

式中：D为梁端纵向位移；DT为由温度引起的梁端纵向位移；DV为由车辆引起的梁端纵向位移；DW为由风荷载引起的梁端纵向位移；DTA为由主梁整体温度变化引起的梁端纵向位移（不包含斜拉索及主塔的影响）；DTD为由主梁温度梯度引起的翘曲效应导致的梁端纵向位移； DTC为由斜拉索温度变化引起的梁端纵向位移（不包含主梁及主塔温度变化的影响）；DTT为由主塔温度变化引起的梁端纵向位移（不包含主梁及斜拉索温度变化的影响）。

由于车辆和风荷载对梁端纵向位移的影响周期为分钟级，而温度对梁端纵向位移的影响周期为1 d，因此，对梁端纵向位移监测数据进行10 min平均之后再分析，则可基本消除车辆和风荷载对梁端纵向位移的影响，剩下的就只有因温度引起的梁端纵向位移，即D=DT。以下对数据的分析均采用10 min平均的方法来消除车辆及风荷载对梁端纵向位移的影响。

2013-01-01南京长江第二大桥北梁端上游侧位移曲线与钢箱梁有效温度之间的关系如图2所示。其中图2（a）是位移与温度的变化趋势曲线，该图显示当温度升高时，位移增大，当温度降低时，位移减小（为了计算和图像显示方便，已将位移值进行了平移和翻转处理），从而可判断梁端纵向位移与温度具有较强的相关性。张宇峰［3］等人对苏通大桥和江阴大桥的梁端纵向位移进行了研究，并发现斜拉桥纵向位移曲线比悬索桥伸缩缝位移曲线光滑，这是由于斜拉索约束了主梁的纵向摆动，即对于悬索桥，DTC=0，而对于斜拉桥， DTC¹0。利用MATLAB软件对纵向位移和温度数据进行线性拟合 D=aT+b，得到图2（b），拟合出的线性方程为：

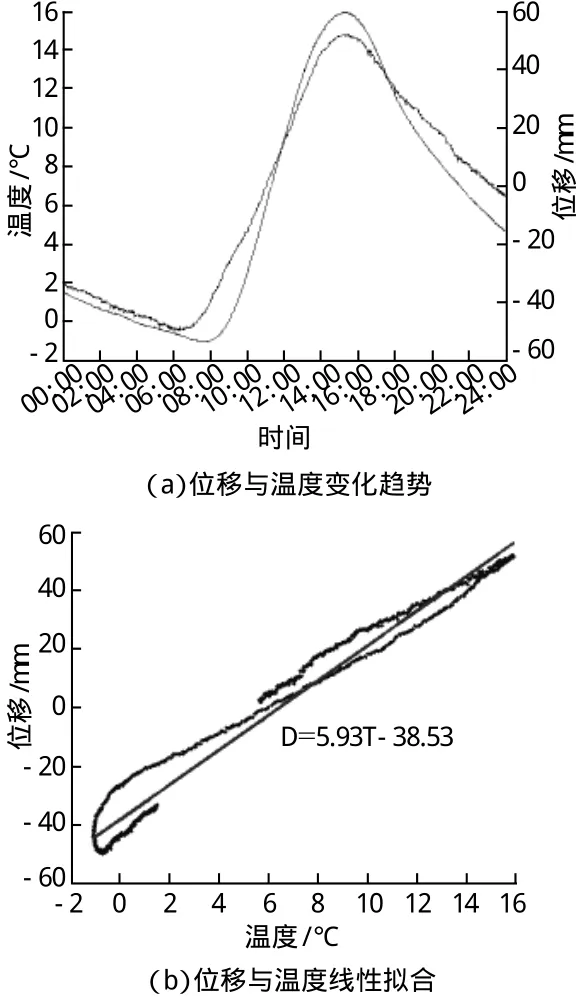
图2 梁端纵向位移曲线与钢箱梁有效温度关系

2013-01南京长江第二大桥北梁端上游侧位移曲线与钢箱梁有效温度之间的关系如图3所示。其中图3（a）显示出该月位移与温度具有相同的变化趋势，图3（b）拟合得到的线性方程为：

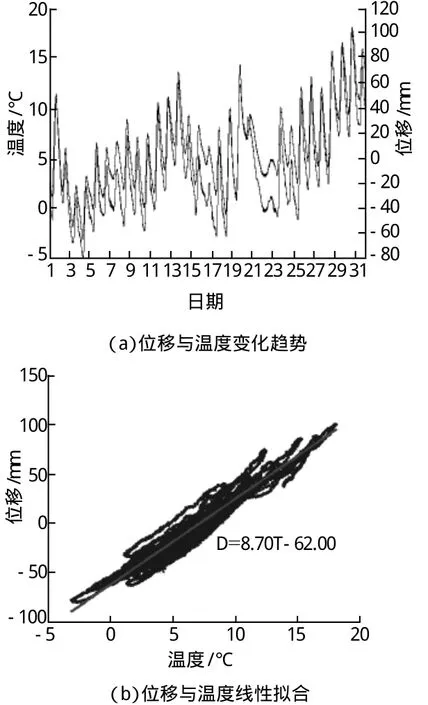
图3 梁端纵向位移曲线与钢箱梁有效温度关系

2013-01南京长江第二大桥梁端纵向位移与温度线性拟合的一次项系数散点图如图4所示，其均值为8.48，按整月数据线性拟合的一次项系数为8.70，两者相差较小。从图4可以看出，南京长江第二大桥梁端纵向位移与主梁有效温度的关系为线性关系，且每一天一次项系数a的变化范围较大，但对于每月的a，其变化基本稳定，2013-01~12拟合线性方程的系数如表1所示，其中一次项系数a在7.58~8.70，平均值为8.18。从图5（a）可知，拟合的线性函数一次项系数a与钢箱梁平均有效温度T仍然具有一定的相关关系，从而拟合得到图5（b），拟合的函数为：

式（5）说明梁端纵向位移与钢箱梁有效温度之间具有一定的非线性关系，但拟合后的非线性函数一次项系数较小。2013年南京二桥的主梁有效温度变化38 ℃，即一次项系数a变化了1.14，约为常数项8.76的13%，说明在较长的时间段或较大的温度变化范围内，斜拉桥伸缩缝位移的非线性确实存在。

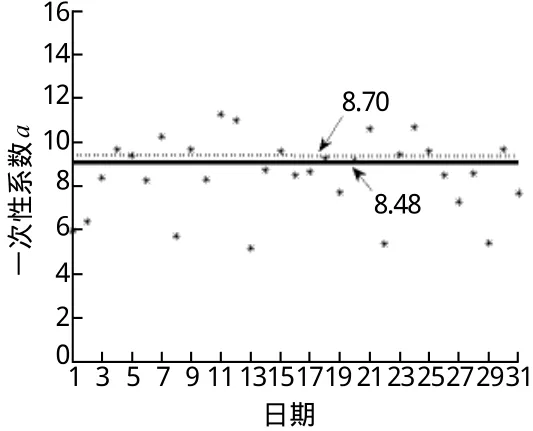
图4 2013-01一次项系数散点图

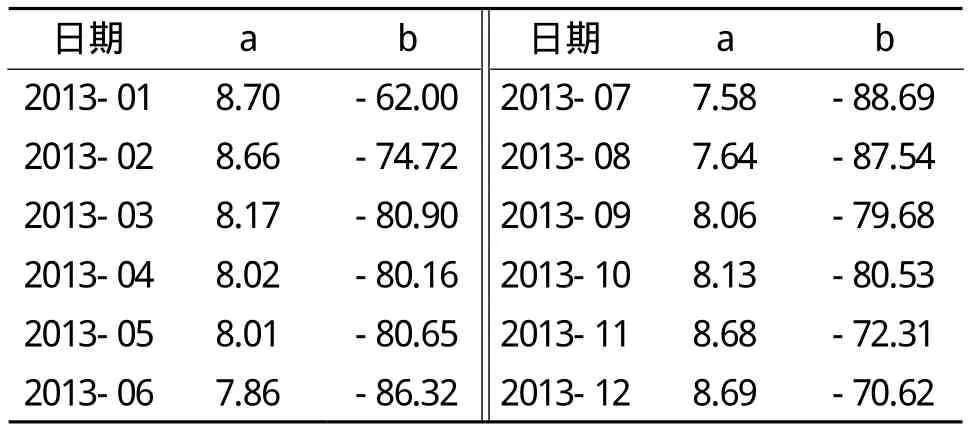
表1 梁端纵向位移与钢箱梁有效温度线性拟合函数D=aT+b

从式（3）和式（4）可以看出，随着温度的升高，主梁向两端伸长，符合热胀冷缩的规律；从式（5）可以看出，随着温度的升高，主梁两端的伸长率逐渐减小，这是由于受到斜拉索的约束和混凝土主塔的膨胀系数与钢结构的膨胀系数不同导致，因此斜拉桥钢箱梁不能自由伸长，而悬索桥主梁基本不受纵向力约束，即悬索桥梁端纵向位移与温度的关系更加接近线性关系，如图5（b）和图6所示，这也是斜拉桥纵向位移形态与悬索桥纵向位移形态不同的重要原因。

梁端纵向位移与钢箱梁有效温度的线性与非线性关系的曲线拟合如图7所示。从两曲线可以看出，在温度-10~40 ℃区间内，两者的差异较小，不到10 mm，而由温度引起的梁端纵向位移量超过350 mm，即相对误差不到3%，因此为了计算和工程应用方便，可以利用线性关系替代斜拉桥梁端纵向位移与钢箱梁有效温度的弱非线性关系。

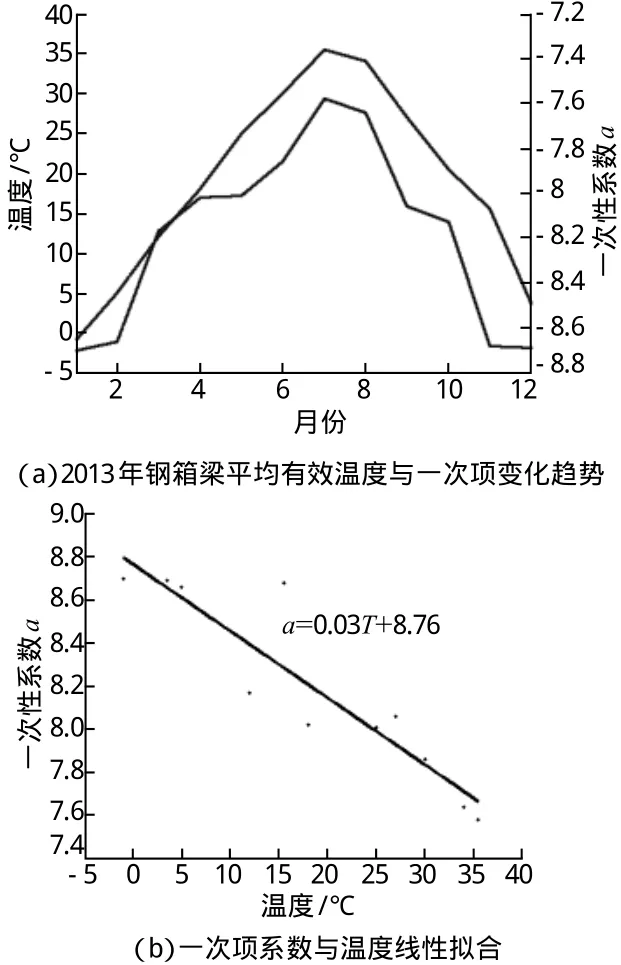
图5 一次项系数与钢箱梁有效温度关系

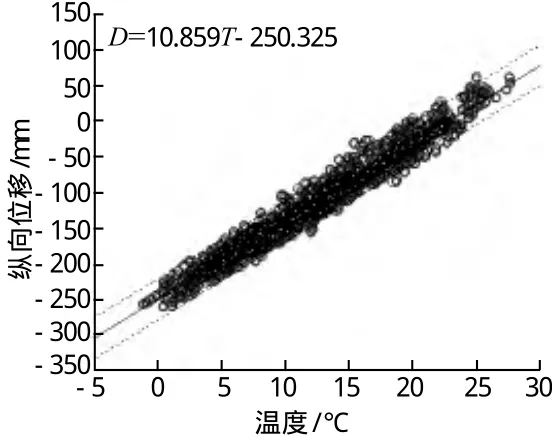
图6 江阴大桥梁端纵向位移曲线与钢箱梁有效温度关系［3］

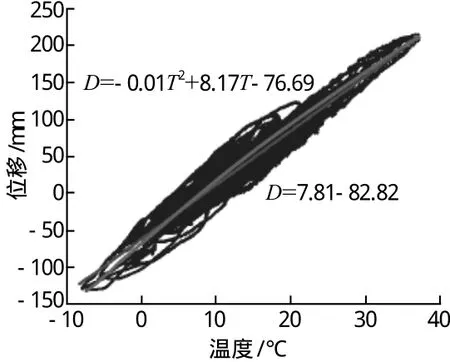
图7 2013年梁端纵向位移与钢箱梁有效温度的线性与非线性关系

4 相关性评估方法

根据上文可知，斜拉桥梁端纵向位移与有效温度的关系具有一定的非线性。但这一非线性效应较弱，可以利用线性替代这一非线性，文献［3］中提出可以利用线性回归法对伸缩缝状态 进行安全评估，对于悬索桥的梁端纵向位移关系，采用线性回归的一次项系数较为稳定；而对于斜拉桥，线性回归的一次项系数变化范围较大，但同样可以利用线性回归对伸缩缝的工作状态进行评估，对多年（一般至少为3年）无异常情况的数据进行线性回归，得到每个月的线性回归系数an，再对an进行概率统计，根据统计特性确定an的安全阈值，当某个月的线性回归系数超过设定的安全阈值，则说明伸缩缝可能出现异常情况，需要进行检修。

5 结论

本文对南京长江第二大桥梁端纵向位移与温度的相关性进行了分析，分别对一天的数据、一月的数据和一年的数据进行了分析，得出以下结论：

（1）斜拉桥纵向位移与主梁有效温度的线性回归曲线的斜率较悬索桥要小，这是由于斜拉索对主梁纵向位移具有约束作用；

（2）当温度变化区间较小时，斜拉桥梁端纵向位移与温度的关系具有较强的线性关系；

（3）由于斜拉索对主梁的几何约束及温差效应，当温度变化区间较大时，斜拉桥纵向位移与主梁有效温度之间具有一定的非线性效应，即斜拉桥纵向位移与主梁有效温度的线性相关性比悬索桥弱；

（4）在对斜拉桥伸缩缝进行安全状态评估和预警阈值设定时，可以直接利用线性关系替代其较弱的非线性关系进行分析。

［1］JTG D60—2004公路桥涵设计通用规范［S］.

［2］李扬海.公路桥梁伸缩缝装置［M］.北京：人民交通出版社，1998.

［3］张宇峰，陈雄飞，张立涛.基于健康监测实测数据的大跨索承桥梁伸缩缝状态分析与评定［C］∥交通运输部长大桥梁健康检测与诊断技术交通行业重点实验室.第四届大跨径桥梁结构损伤预警及状态评估技术研讨会论文集.2012：17-25.

［4］张宇峰，承宇，傅斌，等.基于健康监测实测数据的江阴长江大桥伸缩缝状态分析与评定［C］∥交通部公路科学研究院，东南大学.全国既有桥梁加固、改造与评价学术会议论文集.北京：人民交通出版社，2008：253-258.

［5］苏交科集团股份有限公司.苏通大桥结构健康监测数据分析报告（2011~2012年）［R］.2012.

［6］崔冰，曾宪武，王永珩.南京二桥南汊大桥主桥结构设计［C］∥中国土木工程学会.中国土木工程学会桥梁及结构工程学会第十三届年会论文集.1998：264-272.