广义逆平差法详解
冯浩鉴
(中国测绘科学研究院,北京 100039)
广义逆平差法详解
冯浩鉴
(中国测绘科学研究院,北京 100039)
文献[1]中提出的广义逆平差法又称逆平差法,通过解算广义逆矩阵来解决测量平差问题是该方法的一个亮点。一般读者对广义逆矩阵这个概念可能比较生疏,但本文定义的广义逆矩阵及其求解公式非常简单,很容易掌握,对教学、科研和生产实践有一定参考价值。
广义逆矩阵;平差
一、引 言
处理测量平差问题大致分3个步骤:一是测量误差方程的建立,二是平差模型的选择,三是精度评定。这3个步骤互相联系,互相制约,互相影响。观测误差方程建立后,对平差模型的选择非常重要,它不但决定平差后的观测精度,而且对整个观测对象的客观性产生直接影响。迄今从发表的大量文献来看,对此问题进行研究的论文很少,似乎没有引起必要的重视。本文提供了多种平差模型,可能对各种平差对象的处理起抛砖引玉作用,也可能对一些特殊例子有独到之处,从文献[1]提供的小型算例可以得到一点提示。
二、基础知识
假设矩阵A为非奇异矩阵,则A存在唯一的逆矩阵A-1,满足AA-1=A-1A=E(单位矩阵)。如果方程组AX=B的系数矩阵A非奇异,则方程组存在唯一解X=A-1B。但如果A为奇异方阵或长方形矩阵,则A的逆矩阵就不存在,在这种情况下,需要研究A的广义逆矩阵。
根据不同条件,可以定义A的不同类型广义逆矩阵,本文根据C.R.Rao的著作给出以下定义[2]。
1.广义逆矩阵定义
设矩阵A满足
AA-A=A
(1)
定义A-为A的广义逆矩阵。由定义可得出以下推论:①当A为行满秩矩阵时,则A-=AT(AAT)-1;②当A为列满秩矩阵时,则A-=(ATA)-1AT;③当A为满秩方阵时,则A-=A-1。其中AT为A的转置矩阵。
2.广义逆矩阵唯一性定理
广义逆矩阵A-若满足以下4个条件
(2)
则式(2)中的A-存在唯一解。
证:假设式(2)有两个解
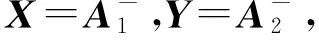
(AXA)TYTY=(XA)TATYTY=
证毕。
三、平差数学模型
1.条件平差
(1) 求平差值
设条件方程为
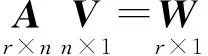
(3)
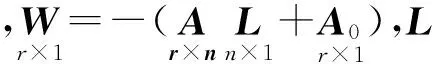
假设V=A-W为式(3)的解,则得
AA-W=W
(4)
因A为行满秩矩阵,依广义逆矩阵的推论得
A-=AT(AAT)-1
(5)
将式(5)代入式(4)得AAT(AAT)-1=E。
由此得
V=A-W=AT(AAT)-1W
(6)
为条件方程式(3)的一个解。下面进一步证明式(6)不但是式(3)的解,而且是唯一解。
证:将式(6)代入式(3)并将其系数矩阵A-代入式(2)的条件(Ⅰ)得
AA-A=AAT(AAT)-1A=A
代入条件(Ⅱ)得
A-AA-=AT(AAT)-1AAT(AAT)-1=A-
代入条件(Ⅲ)得
因此(AA-)T=AA-
代入条件(Ⅳ)得
又由于A-A=AT(AAT)-1A,得
(A-A)T=A-A
证毕。
(2) 求平差值及其函数的相关方差矩阵
① 求一组平差值的相关方差矩阵
设一组平差值为
(7)
式中,符号≅表示该式应用误差传播定律时保持相等关系。
顾及一组观测值相互独立且等精度得
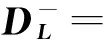
(8)
② 求一组平差值线性函数的相关方差矩阵
设一组平差值线性函数为
式中,F为非对称系数矩阵。其中,元素取决于一组线性函数表达式,F0为常量矩阵。由式(7)得
φ≅FL-FAT(AAT)-1AL=[F-FAT(AAT)-1A]L
由相关方差矩阵同一性规律得φ的相关方差矩阵为
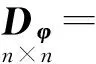
(9)
2.间接平差
(1) 求平差值
设观测误差方程为

(10)
式中,A、X分别为误差方程的系数和未知数(待估参数)矩阵。用分块矩阵改写式(10)得
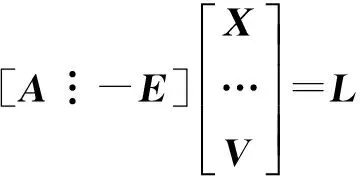
(11)
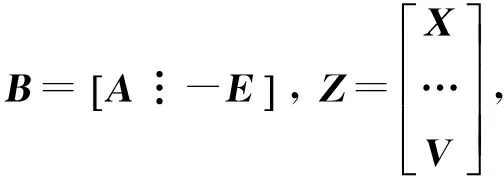
BZ=L
(12)
可将式(11)或式(12)看成条件方程,因B行满秩,所以
Z=B-L=BT(BBT)-1L
(13)
即
(14)
于是
(15)
式中,G-1=[AAT+E]-1。
将B-按式(2)的条件可证得B-的解唯一(证明略)。
(2) 求平差值及其函数的相差方差矩阵
① 求一组平差值的相关方差矩阵
由式(15)第二式得平差值X的相关方差矩阵为
DX=ATG-1DL[ATG-1]T
(16)
顾及观测值li、lj相互独立且等精度,则有
DX=ATG-1μ2EG-1A=μ2ATG-1G-1A
(17)
② 求一组平差值线性函数的相关方差矩阵
设一组平差值线性函数为
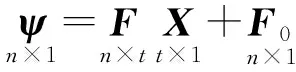
同理得
Dψ=μ2FATG-1G-1AFT
(18)
3.附条件式的间接平差
(1) 求平差值
设观测误差方程为式(11),在t个未知数之间存在条件
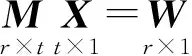
式中,W=-(MX0+A0),X0为未知数的近似值,A0为常量矩阵。组成附条件式的观测误差方程分块矩阵形式为
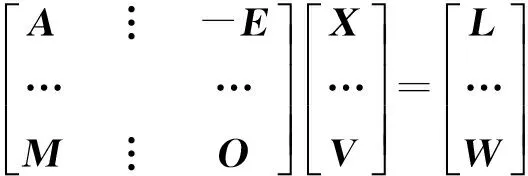
(19)
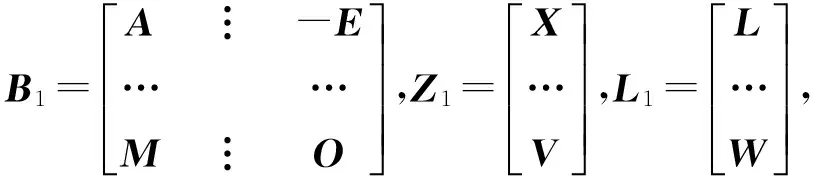
B1Z1=L1
(19)1
式中,O为零矩阵。由广义逆矩阵的定义推论以及唯一性定理得Z1的唯一解为
即
(20)
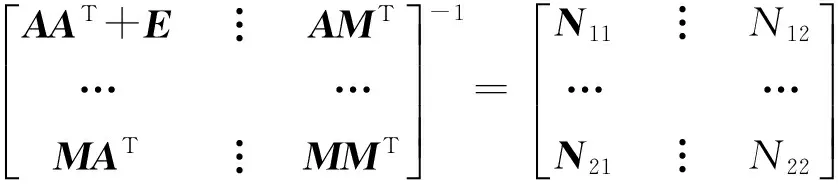
式中,N11、N12、N21、N22分别为逆矩阵解算后的4块矩阵。其中,N11为其左上角的n阶对称矩阵。将它们代入式(20)得
(21)
(2) 求平差值及其函数的相关方差矩阵
由式(21)第一式得X≅[ATN11+MTN21]L,顾及观测值li和lj相互独立、等精度得X相关方差矩阵为
DX=μ2[ATN11+MTN21][ATN11+MTN21]T
(22)
令H1=[ATN11+MTN21],得
(23)
设一组平差值X的线性函数为
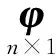
令H2=F[ATN11+MTN21]=FH1,同理得φ相关方差矩阵为
(24)
4.带未知数的条件平差
(1) 求平差值
设带未知数的条件方程为
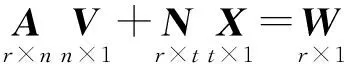
(25)
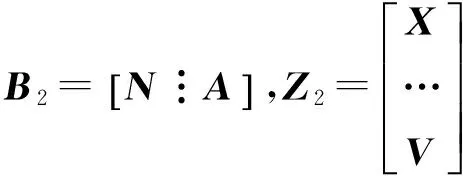
B2Z2=W
因B2行满秩,依广义逆矩阵推论及唯一性定理得Z2的唯一解
即
(26)
(2) 求一组平差值及其函数的相关方差矩阵
① 求一组未知数的相关方差矩阵
由式(26)第一式得
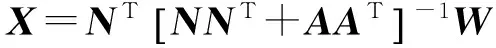
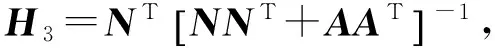
(27)
② 求一组平差值L+V的相关方差矩阵
设一组平差值
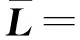
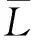
(28)
③ 求一组平差值函数的相关方差矩阵
设平差值一组(t个)线性函数为
令H5=[F+FAT[NNT+AAT]-1A+FxNT[NNT+AAT]-1A]
则得平差值一组(t个)线性函数为
(29)
四、各平差模型方差μ2的估值公式
1.条件平差
由式(6)得
V=AT(AAT)-1W≅-AT(AAT)-1AL
(30)
上式两边取数学期望得
(31)
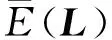
(32)
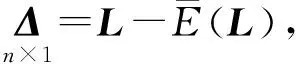
于是
VTV=ΔTAT(AAT)-1AAT(AAT)-1AΔ=ΔTAT(AAT)-1AΔ
(33)
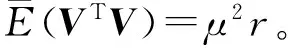
(34)
式(34)为条件平差观测值方差μ2的估值公式,其详细推导过程可参考文献[3]。
2.间接平差
(35)
将式(35)减式(15)第一式得
因此
(36)
假设
其对角线上元素分别为
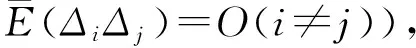
令k1=(at)11+(at)22+…+(at)nn
则得
于是得
(37)
式(37)为间接平差观测值方差估值的实用公式。其中,k1为G-1G-1对角线上元素之和。因G-1为对称方阵,将k1展开后不难发现,其和即为G-1中每个元素平方之和。
3.附条件式的间接平差
由式(21)第二式得
V=-N11L+N12W≅-N11L
(38)
两边取数学期望得
(39)
由式(39)减式(38)得
(40)
上式两边取数学期望值得
(41)
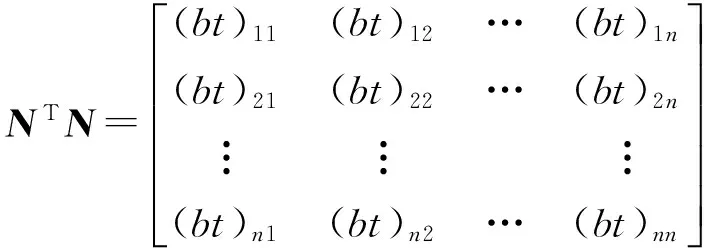
将其代入式(41)展开后,两边求数学期望值并顾及观测值相互独立、等精度得
令k2=(bt)11+(bt)22+…+(bt)nn,于是得
(42)
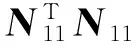
4.带未知数的条件平差
由式(26)第二式得
(43)
两边取数学期望得
(44)
将式(43)减式(44)得
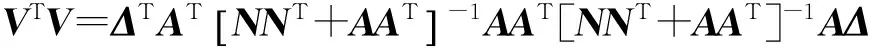
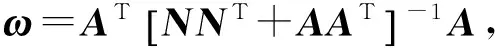
VTV=ΔTωωΔ
两边取数学期望值得
(45)
假设
代入式(45)展开后顾及观测值相互独立、等精度得
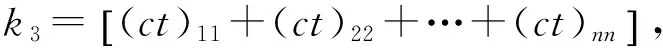
(46)
式(46)为带未知数条件平差估值μ2的实用公式。其中k3为ωω矩阵对角线元素之和,其和等于ω各元素平方值之和。因为AT[MMT+AAT]-1在解算V值的过程中已知,将其左乘矩阵A即得ω。
式(34)、式(37)、式(42)和式(46)分别为条件平差、间接平差、附条件式间接平差以及带未知数条件平差求解观测值方差的实用公式。
五、结束语
纵观全文,可看到一整套与最小二乘平差法推理过程完全不一样的平差方法。这种区别源于两者立论的基本思想不同。前者依据观测误差平方和最小的基本思想出发,运用微分学的基础知识导出一套最小二乘平差法;后者根据广义逆矩阵特性及其唯一性定理建立另一套平差法——广义逆平差法。笔者曾用矩阵代数及其微分理论,按本文讨论的4种平差模型演绎过最小二乘平差法全过程[5],如果将其与本文作一比较,两者的区别一目了然。在本文中,广义逆矩阵贯穿在各个平差模型的求解过程中。特别要指出的是,所求的广义逆矩阵不但唯一,而且可以通过一般的、众所周知的矩阵求逆方法答解,这就是广义逆平差法最主要的特点。
[1] 冯浩鉴.广义逆平差理论及其应用[J].测绘科学,2009,34(4):5-8.
[2] RAO C R.Linear Statistical Inference and Its Application[M].[S.l.]: John Wileg and Sons Inc,1973.
[3] 冯浩鉴.相关平差概论[M].北京:测绘出版社,1982.
[4] 魏木生.广义最小二乘问题的理论和计算[M].北京:科学出版社,2006.
[5] 冯浩鉴.矩阵代数在最小二乘法中的应用[J].数学通报,1963(6):31-36.
Explaining in Detail for Generalized Inverse Adjustment
FENG Haojian
冯浩鉴.广义逆平差法详解[J].测绘通报,2015(7):27-31.
10.13474/j.cnki.11-2246.2015.0204
2015-01-03
冯浩鉴(1936—),男,研究员,长期从事大地测量、测量平差等方面的研究。E-mail:fangaip@casm.ac.cn
P22
:B
:0494-0911(2015)07-0027-05

