一类球体与柱体组合问题的通用“秒杀”解法
☉内蒙古师范大学附属中学张生
一类球体与柱体组合问题的通用“秒杀”解法
☉内蒙古师范大学附属中学张生
组合体问题是立体几何的常考点,也是高考热点,此类问题对学生的空间想象能力要求很高·通常以三视图为命题背景,或以与球体有关的组合体为背景,本文就球体与柱体的组合问题,给出一种通用解题方法,并给出具体实例来说明方法的通用性·
一、球体与柱体的组合问题的基本模型
图1所示的是一个半圆和其内接矩形旋转360°后形成球体与柱体的组合体,其中,满足两个关系式:R2=r2+ d2,d=(其中,球体半径为R,圆柱半径为r,圆柱高为h,圆柱底面到球心的距离为d),这两个关系式揭示了球体与柱体组合体的内在联系,即在R,r,d三个变量中,可实现“知二求一”·
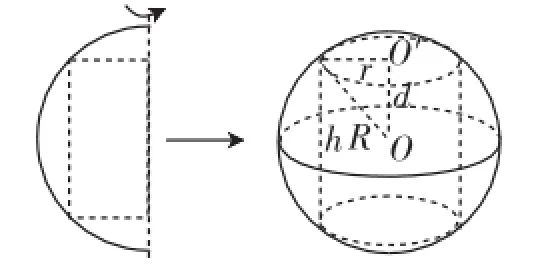
图1
这个模型可以引申为其他柱体与球体的组合体问题,比如直三棱柱与球体、直四棱柱与球体、直六棱柱与球体等,我们只需确定r即可,此时r的含义为棱柱外接圆柱的半径,转化为平面图形即为多边形外接圆的半径,通常会有如图2~图6所示的情况·
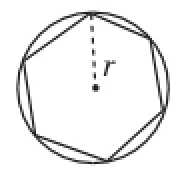
图6
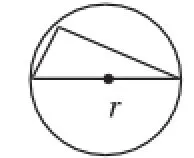
图2
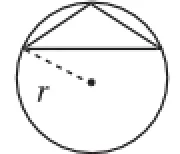
图3

图4
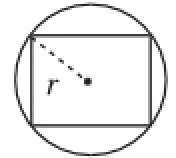
图5
二、应用模型解题
例1(2013年辽宁卷第10题)已知三棱柱ABCA1B1C1的6个顶点都在球O的球面上,若AB=3,AC=4, AB⊥AC,AA1=12,则球O的半径为()·
解析:本题为直三棱柱与球体的组合问题,且三棱柱的底面三角形为直角三角形,易得斜边长为5·高为12,用模型,秒杀此题!
例2(2014年陕西卷第5题)已知底面边长为1,侧棱长为2
■的正四棱柱的各顶点均在同一个球面上,则该球的体积为()·

解析:本题为正四棱柱与球体的组合问题,由底面边长为1易得其外接圆半杀此题!
例3(2009年全国卷第15题)直三棱柱ABC-A1B1C1的各顶点都在同一球面上,若AB=AC=AA1=2,∠BAC= 120°,则此球的表面积等于_________·
解析:本题为直三棱柱与球体的组合问题,且三棱柱的底面三角形为等腰三角形,顶角为120°,易得r=2,4πR2=20π·
例4一个正四棱柱的各个顶点在一个直径为2cm的球面上,如果正四棱柱的底面边长为1cm,那么该棱柱的表面积为_________cm2·
例5(2008年新课标第14题)一个六棱柱的底面是正六边形,其侧棱垂直底面·已知该六棱柱的顶点都在同一个球面上,且该六棱柱的体积为底面周长为3,那么这个球的体积为________·
以上例题充分说明模型的重要性,只要理解模型实质,可以说,此类问题不再是难题,读完题后直接套用模型秒杀问题!这是多么有趣的数学现象·
三、重要结论及应用
结论1:若高为h的正棱柱或圆柱内接于半径为R的球O中,则当且仅,柱体的体积取得最大值·证明:由基本模型知R2=r2+d2,d=,其中,r为圆柱的半径(或正多边形外接圆的半径),上式可化为r2=R2-
而正棱柱或圆柱的底面积都可化为一个r的二次函数,即S底=λr(2λ为常数)·②
所以,V=S底h=λr2h·③
由④式知体积是关于高的三次函数,可通过求导来计算最大值·
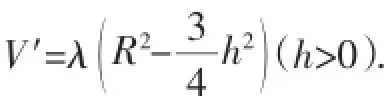
下面具体给出正三棱柱、正四棱柱、正六棱柱、圆柱对应的体积的最大值:
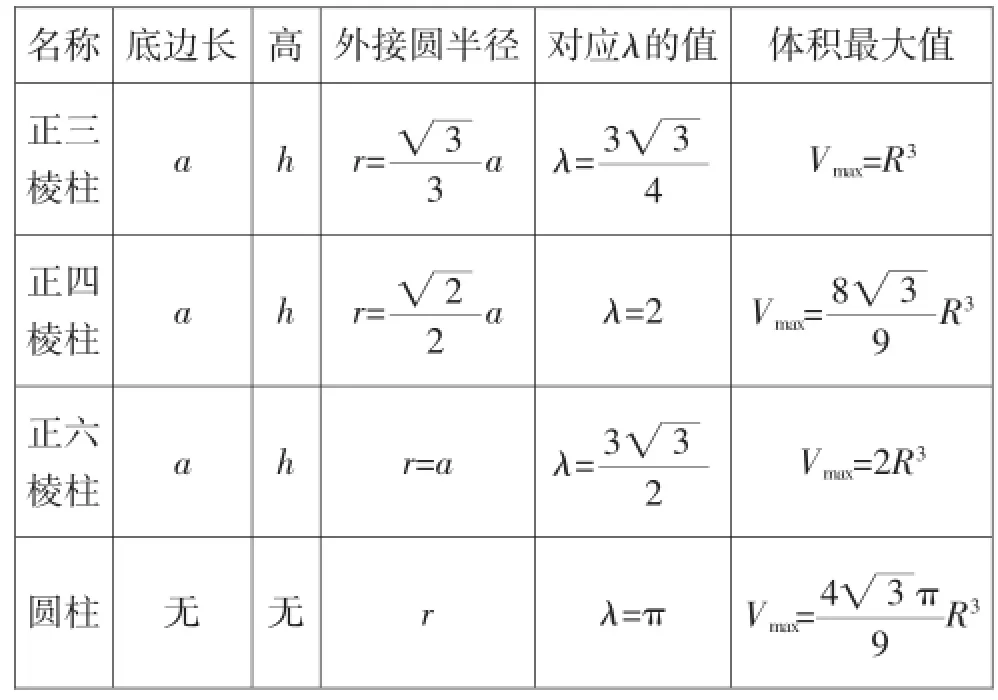
名称底边长高外接圆半径对应λ的值体积最大值正三棱柱a h r=3■■3aλ=33 4 Vmax=R3正四棱柱a h r=2■■2a λ=2Vmax=83 9R3正六棱柱a h r=a λ=33■2 Vmax=2R3圆柱无无r λ=π Vmax=43■π9R3
结论2:若高为h的正棱柱或圆柱内接于半径为R的球O中,则当且仅当R时,柱体的侧面积取得最大值·
下面具体给出正三棱柱、正四棱柱、正六棱柱、圆柱对应的侧面积的最大值:
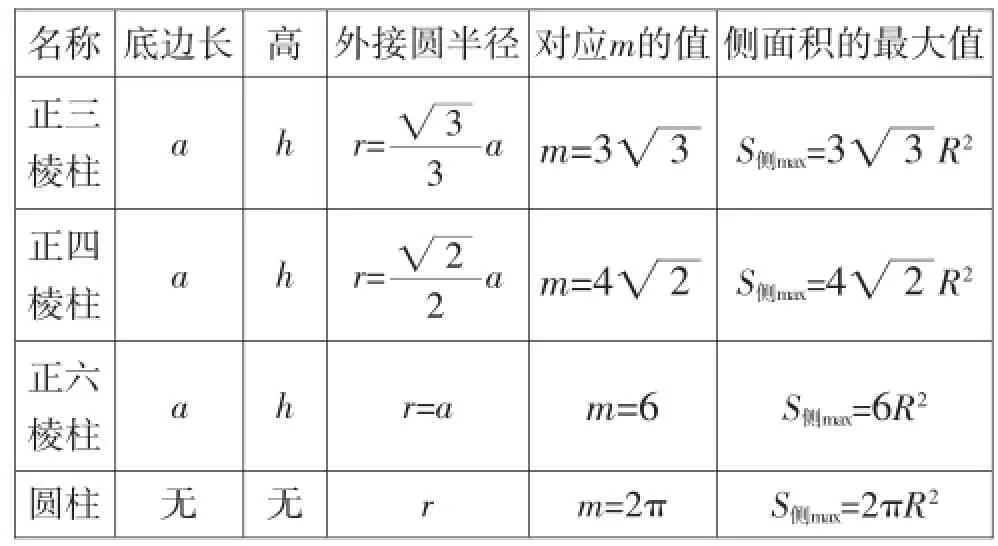
名称底边长高外接圆半径对应m的值侧面积的最大值正三棱柱a h r=3■■S侧max=33 3am=33■R2正四棱柱a h r=2■■S侧max=42 2am=42■R2正六棱柱a h r=a m=6 S侧max=6R2圆柱无无r m=2π S侧max=2πR2

