数列单调性问题探究
☉辽宁省沈阳市教育研究院王恩宾
数列单调性问题探究
☉辽宁省沈阳市教育研究院王恩宾
这是一堂关于高三复习中数列问题的一个小的专题·该课对数列的单调性与函数的单调性进行了有机的结合,将二者的区别与联系进行了剖析·利用信息技术将数列的单调性和函数的单调性进行了形象的描绘,在此过程中数形结合思想得到了渗透·通过对问题不同解法的探求,开拓了学生的视野,发散了学生的思维·通过编写相似题型,激发了学生的学习潜力,拓宽了眼界,培养了创新能力和创新意识·
一、开场白
师:同学们好,前面已经复习了函数和数列的基础知识,对数列与函数有了比较深入的了解·数列和函数有着千丝万缕的联系,数列可以看作是一个函数,当自变量为正整数(或它的有限子集)时,自变量从小到大依次取值时所对应的一列函数值·因为从数列第二定义可以看出数列就是一列函数值,所以很多数列问题都可以借助函数的性质进行解答·
二、巩固基础
师:在前面给大家的导学案中给出了学生自主学习的内容,下面请各小组在小组内用2分钟时间交流、修正自主学习的问题,并请一名同学进行实物展示自主学习的第一个问题·
生1:我要展示的是自主学习部分的问题1·
问题1:数列的单调性的定义·
递增数列的定义:如果数列{an}满足an<an+1,那么称数列{an}为递增数列;
递减数列的定义:如果数列{an}满足an<an+1,那么称数列{an}为递减数列·
师:生1同学关于数列递增、递减的定义非常准确,但有时在证明数列的递增(或递减)时还经常应用an-1<an(或an-1>an),此时一定要注意n≥2,n∈N+这一前提条件,即证明后一定要验证n=1时结论是否成立,这是学生解题过程中经常出现错误的地方,一定要引起足够的重视·
生2:我要展示的是自主学习部分的问题2·
问题2:等差数列、等比数列的单调性·

数列单调性及其满足的条件递增数列,d>0不增不减,d=0递减数列,d<0等比数列递增数列,a1>0,q>1(或a1<0,0<q<1)递减数列a1>0,0<q<1(或a1<0,q>1)等差数列
师:该同学很好地将等差数列和等比数列这两个重要数列递增、递减的条件进行了整理,做的非常好·如果将等差数列、等比数列单调递增、递减的这些条件和结论通过图像的形式进行记忆,那么效果会更好·如图1所示,是老师作出的数列an=a1qn-1在a1>1,q>1时,条件、结论、图像三者有机结合的一个反映数列单调递增的图像·请同学们课后用GeoGebra软件将其他情况下数列增减性的图像作出来·
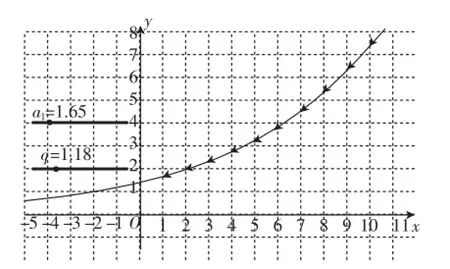
图1
三、源于教材
师:导学案上两个自主探究的问题都是选自教材上的问题,下面我们研究第一个问题·
问题3:(必修5P39)已知两个等差数列的公差不相等,但第5项相等,这两个等差数列中除了第5项外,还有序号相同且数值相等的项吗?为什么?
生3:设等差数列{an},{bn}的公差分别为d1,d2,且d1≠d2,a5=b5·假设两个等差数列中除了第5项外,还有序号相同且数值相等的项,那么an=a5+(n-5)d1=bn=b5+(n-5)d2,得到d1=d2,与已知d1≠d2相矛盾·因此,两个等差数列中除了第5项外,没有其他序号相同且数值相等的项·
师:该同学利用反证法推导出等差数列不存在项数和项完全相同的情况,推理过程很严谨·还有没有同学用其他方法解答此问题?
生4:因为等差数列an=a1+(n-1)d1=d1n+(a1-d1)可以看作是自变量为正整数(或有限子集)的一次函数(或常数),当自变量从小到大依次取值时,对应的是一列函数值,所以点(n,an)一定落在直线p:y=d1x+(a1-d1)上·
同理:点(n,bn)一定落在直线q:y=d2x+(a1-d2)上·因为两个数列{an},{bn}具有相同的第5项,所以直线p,q有一个交点(5,a5)·因为两条直线在斜率不同的情况下最多只能有一个交点,不会有第二个交点,所以也不会存在这样的数列,除了第五项之外再有序号相同且数值相等的项·
师:该同学将等差数列的通项公式与一次函数图像有机地建立联系,将抽象的代数问题几何化,借助几何图形直观形象地对问题进行了阐述·虽然没有画图,但数形结合思想在解答中完美地得到了体现,值得鼓励·
师:自主探究中还要求探究问题4·
问题4:(必修5P48)已知两个等比数列的公比不相等,但第5项相等,这两个等比数列中除了第5项外,还有序号相同且数值相等的项吗?为什么?
生5:设等比数列{an},{bn}的公比分别为q1,q2,且q1≠q2,a5=b5·假设两个等比数列中除了第5项外,还有序号相同且数值相等的项,那么an=a5·qn-51=bn=b5·qn-52,得到qn-51=qn-52,如果n-5为偶数,那么q1=-q2是符合要求的,与已知q1≠q2不矛盾·
因此,两个等比数列中除了第5项外,还有其他序号和数值均相等的项·
例如:等比数列an=2n-1,bn=(-2)n-1的奇数项相同,偶数项互为相反数·
师:图2所示的是给出的公比互为相反数的两个等比数列的图像的对照图·当公比为负数时,对应的数列为摆动数列,正负交替出现,图中三角形点、圆形点部分分别为的图像(注意三角形点和圆形点重合的点)·
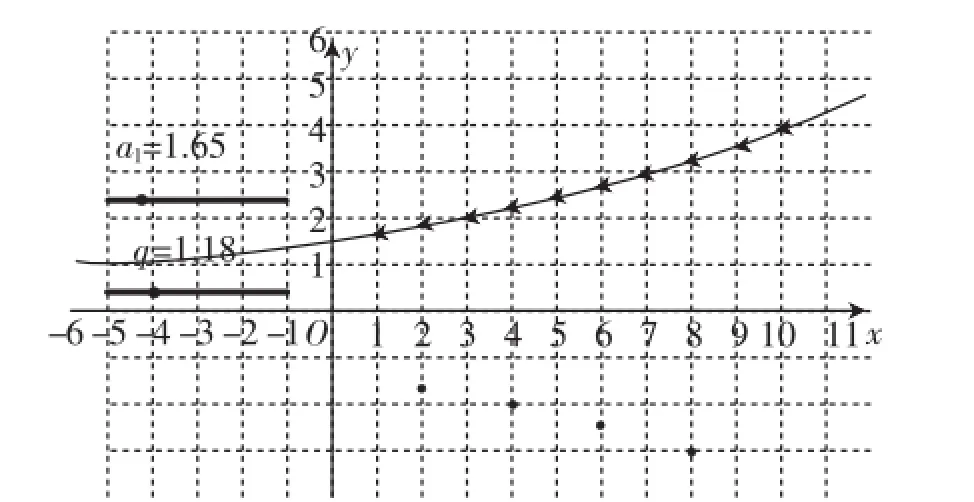
图2
师:前面回顾了数列单调性的定义,下面用5分钟时间结合数列单调性的定义各小组给出教材上问题5的不同的解题思路和解题方法·
问题5:(必修5P28)若数列{an}的通项公式是an=是第几项?
生6:要判定数列项的最大值和最小值,可以先判定数列的变化规律,根据数列的变化规律再考虑数列的最大项和最小项·

师:该同学首先利用定义判定了数列的变化规律,再利用分离系数的方法确定数列各项的大小关系,推理过程严密·但是,此种方法运算的过程比较麻烦,对抽象思维的要求比较高,计算量较大,因此用此种方法很多同学还存在一些困难·除了用上面的方法确定数列项的大小外还可以用什么方法解答?
其次,在函数图像上作出数列的各个点(n,an);
第三,根据函数图像数形结合就可以得到第10项最大,第9项最小·
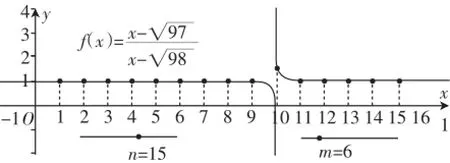
图3
师:哪位同学还能提出不同的解题思路?
师:该同学的思路非常好,此种方法是将an=与过两点A(x,y),B(x,y)直线的斜率公式k=1122相对比可知,a相当于过两点M(n,n),N(
n)的直线的斜率,因此当n变化时,动态的M点与静态的N点形成的线段的斜率的最大值就是要求的an的最大值·从理论上看这种思考方法非常的好,但由于点M(n,n)都在直线y=x上,点N(虽然不在直线y=x上,但是相对的位置非常接近,所以用肉眼很难判定斜率的大小·如图4所示,即使用计算机作出的图形也无法判定斜率的不同·由于此题中点的特殊性,因此此题不适合用此方法·但是,如果N点不在M点所在的直线附近,那么此种方法可以采用,并且可以起到一目了然的作用·
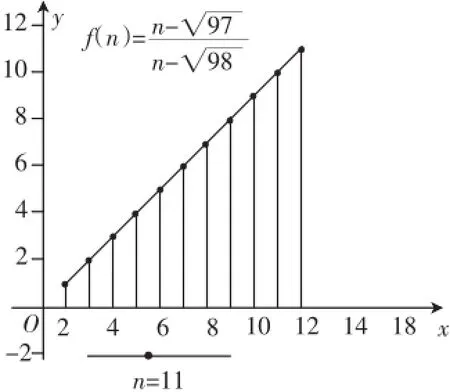
图4
师:从上面三种解题方法看,请一个同学谈一下自己的体会·
生9:解决数列单调性问题可以从以下几方面考虑:
(1)首先想一想从哪些角度可以解决此问题,确定解决此问题的思路或方向·
(2)若从函数角度解决问题,则需要将数列问题抽象为函数问题,利用函数的图像和性质进行解题·
(3)因为数列和函数有很多可以相通的地方,所以数列问题可以借助函数进行解题,但数列并不是函数,因此要注意二者的区别·
师:该同学总结的非常好·
四、高于教材
师:刚才我们研究了教材上的习题,同学们有很多好的解答问题的方法·下面给大家几分钟的时间,请各个小组设计一个与问题5类似的试题,并说明设计思路·
生10:我们小组考虑改变两个常数为变化的数值,将问题从特殊变换成一般·
设计问题1:数列{an}的通项公式是λ∈N+,它的前n项中最大的项是第几项?最小的项是第几项?如图5所示的图像是我们借助GeoGebra软件制作的取不同值时的图像·
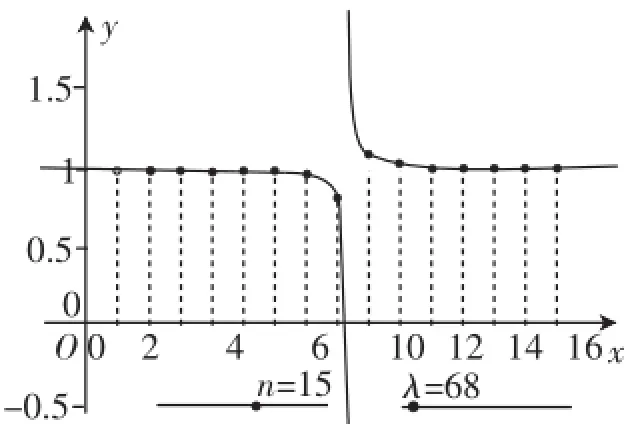
图5
生11:小组2的同学研究了分式函数上数列的单调性变化情况,常见的函数当然包括二次函数,因此我们设计的题目是针对二次函数进行设计·
设计问题2:数列{an}的通项公式是an=n2+2n,n∈N+,它的前n项中最大的项是第几项?最小的项是第几项?
师:两个小组的设计非常好,能够将常见的函数与数列进行有机的整合,为数列单调性问题的分类提供了依据·下面结合该小组同学的设想看下面的问题·
五、问题探究
问题6:若数列{an}的通项公式是an=n2+λn,{an}是单调递增数列,求实数λ的取值范围·
生12:因为数列{an}的通项公式是an=n2+λn,{an}是单调递增数列,所以an+1>an,所以(n+1)2+λ(n+1)>n2+λn,所以λ>-(2n+1)·因为-(2n+1)max=-3,所以λ>-3·
师:该同学利用递增数列的定义建立关于n、λ的不等式,通过分离系数得到关于λ的恒成立不等式,因此λ只需大于-(2n+1)的最大值-3即可·
师:除了上面的解法还可以怎么考虑此问题?
生13:若将an=n2+λn看成关于二次函数,则此函数的图像是开口向上的抛物线,点(n,an)都是抛物线上的点·如果函数an=n2+λn的对称轴n=≤1,即λ≥-2时,根据二次函数图像的特点,都有an+1>an,此时数列为递增数列·
师:该同学能够将an=n2+λn看成关于n的二次函数,并利用二次函数的图像和性质来研究数列的单调性,很好地在函数与数列之间建立起联系的桥梁,体现了数形结合思想·但是,考虑到了函数和图像间的联系,却忽略了函数与数列之间的区别·数列是一列特殊的函数值,因此数列的单调性既与函数的单调性有联系,又与函数的单调性有区别·
(1)如果函数an=n2+λn的n=1,即λ≥-2时,根据二次函数图像在对称轴右边单调的特点,都有an+1>an,此时数列{an}为递增数列;
所以λ<-2,且1+λ<22+2λ,所以-3<λ<-2·
综上(1)(2)所述,实数λ的取值范围是λ>-3·
六、巩固加深
师:利用上面研究问题的方法解答下面的问题·
问题7:已知数列{an}的通项公式是若{an}是单调递增数列,求实数λ的取值范围·
生14:因为{an}是单调递增数列,所以a以λ<n(n+1)min=2,所以λ<2·
师:该同学的方法思路简单,根据数列单调性的定义,很容易将数列递增的问题转化为不等式恒成立问题,再求参数的取值范围·下面请同学们利用函数的性质进行解答·
n
师:该同学解答问题的思路很好,能够将数列和函数联系在一起研究,但是该同学在思考问题时,人为地将λ的取值范围进行了缩小,造成解答问题不够全面的情况·因为实数λ的取值范围没有确定,所以对λ的取值情况要根据函数的不同情况进行分类讨论,再将各种情况进行合并,找到符合要求的λ的取值范围·下面请各小组将该问题的解答补充完整·
生16:根据老师刚才的提示,我们小组认为函数(fx)= x+为对号函数的条件是λ>0,所以还要对λ<0,λ=0两种不同情况进行思考·我们小组分三种情况进行讨论·
(2)当λ=0时,an=n为单调递增数列;
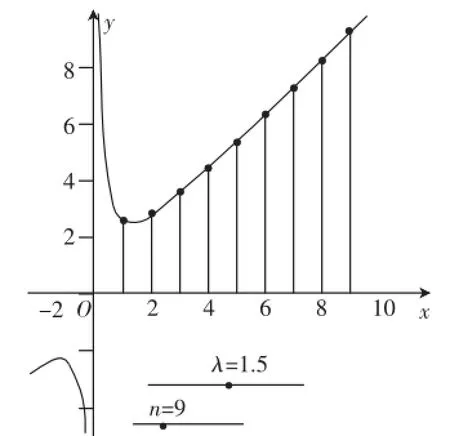
图6
综上(1)(2)(3)所述,{an}是单调递增数列时,实数λ的取值范围是λ<2·
师:该同学的解法中,首先,将数列问题和函数问题结合在一起,利用函数思想解决数列问题;其次,利用分类讨论思想将对函数不同的情况进行了讨论;第三,实现了数列的单调递增与不等式组的等价转化·
七、举一反三
师:通过问题1~问题7的学习,复习、巩固、引申了数列单调性,对数列的单调性有了比较深入的理解·请各小组结合教材上与单调性有关的问题8提出自己小组设计试题的思路和想法·
(1)求证:an>-2;
(2)数列{an}是递增数列还是递减数列?为什么?
师:该小组的同学能够利用信息技术手段研究数学问题,开辟了数学新的研究方式·数学已经不仅仅进行逻辑推理得出结论,数学已经变成了一个实验性的学科,将会有更多的数学结论通过实验被发现·此种思路很好,课后请同学们按照该小组提出的设计思路命制出符合要求的试题·
生18:我们小组考虑的是问题中给出的是分式函数,如果在此函数的基础上乘以一个x+a,那么函数将变成k(x)=(x+a)f(x)的形式,整理、换元后该函数k(x)是关于x的“对号函数”形式,并且含有参数a,这样就可以设计出下列问题·
师:该小组同学从另一角度思考了这一问题,通过一个简单的变形,将一个问题转化为另一问题,将前面研究的两个试题整合在一起,这种思考问题的方法可以大大地拓宽试题的设计思路,命制出更好的试题·
八、课堂小结
师:下面请各小组对本节课进行小结·
生19:复习巩固了数列单调性的定义,并能应用定义判断数列的单调性·
生20:能够将数列的单调性与函数的单调性进行整合,借助函数的单调性研究数列的单调性·
生21:利用信息化手段可以进行数学试验获得数学结论,探索获取新知识、新结论的方法·
生22:通过举一反三环节可以有效地培养创新意识和创新能力·
九、反思启发
什么样的课是好课?不同的人对好课的理解会有所不同·比如:华东师范大学教授叶澜认为:一堂好课没有绝对的标准,但有一些基本的要求·
(1)有意义:学生的学习首先是有意义的·初步的意义是他学到了新的知识;进一步是锻炼了他的能力;往前发展是在这个过程中有良好的、积极的情感体验,产生进一步学习的强烈要求;再发展一步,是他越来越会主动投入到学习中去·对于高三复习来说问题的选取要源于教材、高于教材,要将高考的要求与教材上的例题、习题有机地结合在一起·在本节课中几个试题的原型都来自于教材,因此从有意义的角度看,完全符合要求·
(2)有效率:一是对面上而言,这节课下来,对全班学生中的多少学生是有效的,包括好的、中间的、困难的,他们有多少效率;二是效率的高低·有的高一些,有的低一些,但如果没有效率或者只是对少数学生有效率,那么这节课都不能算是比较好的课·从这个意义上讲,这节课应该是充实的课·整个学习过程,有课前的复习总结、有课上的展示发言、有问题的拓展引申、有课后的完善,课上、课下大家都有事情干,通过教师的点评,学生都能从中获得启迪,整个课堂的容量很大·
(3)生成性:本节课不完全是预先设计好的,而是在课堂中有教师和学生真实的、情感的、智慧的、思维和能力的投入,有互动的过程,气氛相当活跃·在本节课中,既有资源的生成,又有过程状态的生成,既研究试题本身的变化,又研究试题所反映出的本质特点,学会对试题进行归类,这样的课可称为丰实的课·
(4)常态性:平时的教学离不开教材,善于对教材上的试题进行总结、分类、合并、变形是教学的常态,本节课就很好地反映了这一点·
(5)有待完善:本节课还有需要完善的地方,特别是在短时间内研究了这么多的问题,即使学生课前有所研究,但时间上还是显得比较紧张·只要是真实的课就会有缺憾,课不能十全十美,十全十美的课造假的可能性最大,有缺憾是真实的一个指标,笔者喜欢上这样的课·生活中的课本来就是有待完善,这样的课称之为真实的课·扎实、充实、平实、真实,说起来好像很容易,真正做起来却很难,但正是在这样的一个追求过程中,教师的专业水平才能提高,心胸才能博大起来,同时也才能真正享受到:“教学的过程是一个创造性的过程,也是欢乐和智慧的体验过程”·F

