基于拓扑优化的薄板加筋方法研究

钟焕杰，金海波

(南京航空航天大学飞行器先进设计技术国防重点学科实验室，江苏南京 210016)

薄板加筋结构因其跨度大、质量轻、结构效率高等特点被广泛应用在航空航天、船舶、汽车等工业领域，这种结构一般都是由薄板和相应的加强筋组成的。对薄板结构进行加筋处理，能够以不增加结构质量为前提而改善结构的相关性能，加筋处理已成为提高薄板结构力学性能的主要方法之一。

薄板加筋结构可以通过改变筋条的截面形式、筋条间距以及筋条和薄板自身的尺寸来满足工程实际对加筋板结构强度、刚度和稳定性等多方面的要求。常规的加筋板优化设计，可以先按满应力设计计算出相应载荷下的等效蒙皮厚度，然后选取一定的加筋比和厚度比对该等效板进行稳定性设计。

拓扑优化方法将结构的拓扑布局作为主要的设计变量，通常要求在一定的设计空间内寻找出最优的材料分布形式，在满足结构相关力学性能的前提下使结构质量最小化［1］。如果将拓扑优化设计方法跟薄板加筋优化设计联系起来，可以将薄板中的筋条布局设计问题转化为薄板中材料的分布问题。本文主要对常规的薄板加筋设计提出一个合理的优化流程，然后将拓扑优化方法应用于薄板加筋设计中，实现以拓扑优化指导薄板加筋。

1 常规的薄板加筋设计

1.1 蒙皮和筋条的优化设计

在薄板加筋结构中，如果筋条间距较大，筋条较高，容易出现蒙皮局部屈曲和筋条腹板局部屈曲;如果筋条间距较小，筋条数量多、高度小，则容易出现加筋板结构的总体屈曲。因此，合理地协调筋条和蒙皮之间的材料配置及其相关的尺寸参数就显得尤为重要［2］。

对一块在轴压载荷下四边简支的长方形薄板进行加筋时，首先根据满应力设计计算出该薄板的等效蒙皮厚度T:

式中:F为矩形薄板的轴压载荷;［σ］为材料许用应力;W表示矩形薄板的宽度。

将横截面中筋条跟蒙皮的截面积之比定义为加筋比K1，将筋条跟蒙皮的厚度之比定义为厚度比K2，可表示为:

式中:Sst和Ssk分别表示筋条和蒙皮的横截面积;tst和tsk分别表示筋条和蒙皮的厚度。本文中的筋条采用矩形筋条，筋条高度为h，则筋条和蒙皮的横截面积可表示为:

式中:N表示加筋板结构中的筋条个数。这样，就将等效蒙皮的材料按加筋比分配给了筋条和蒙皮，材料分配前后横截面面积应该是相等的，则:

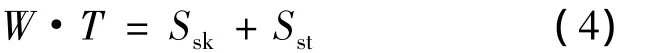
联立公式(2)、(3)、(4)，得蒙皮厚度为:

由薄板屈曲理论可知薄板屈曲理论公式如下［3］:

式中:σcr为薄板临界屈曲应力;E为材料弹性模量;b为薄板受压边宽度;t为薄板厚度;系数k的取值受载荷形式、四边支持情况以及薄板长宽比等影响。对载荷形式为压缩载荷、四边简支且长宽比大于1的薄板而言，k=4。由于加筋板筋条间的蒙皮受筋条的支持，致使其四边支持情况处于简支跟固支之间，引入一个筋条支持系数的概念kr，则系数k=4kr，其中kr取值跟加筋板结构参数有关，在此取值为1.4。

此时，由式(6)可知，为了保证加筋板蒙皮局部屈曲临界应力与材料许用应力相同，筋条间距w的计算公式可表示为:

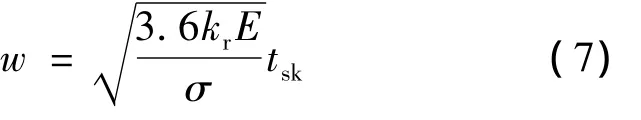
通过筋条间距w可得矩形薄板的加筋个数N:

式中必须对N进行向上取整。

最后，联立式子(2)、(3)、(4)，可得筋条高度:

至此，则计算出了满足蒙皮局部屈曲要求的加筋板截面所有参数。

1.2 肋间距的优化设计

对于总体屈曲要求，可根据加筋板总体屈曲理论公式来优化肋间距从而满足其总体屈曲要求，总体屈曲公式如下:

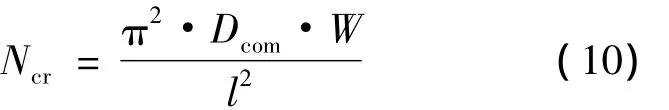
式中:Ncr为临界屈曲载荷;l为肋间距;Dcom为加筋板轴向弯曲刚度系数。加筋板轴向弯曲刚度系数计算公式如下:

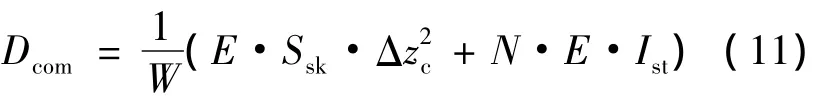
式中:Δzc为蒙皮块截面的中心面到组合截面形心轴之间的距离;Ist为每一根筋条相对于组合截面形心轴的惯性矩。通过肋间距l可求得矩形薄板的加肋个数M:

至此，则对长宽比固定的受轴压载荷的四边简支矩形薄板进行了强度和稳定性设计。

1.3 稳定性设计流程

上面两小节主要讨论了如何在加筋比K1和厚度比K2确定的前提下，设计出满足蒙皮局部屈曲和总体屈曲要求的加筋板结构。但是，在设计之初加筋比和厚度比的选取具有一定的随意性，一般由于设计人员根据工程经验选取。本文则提出一个设计流程，即对于一块长宽比不变的等效厚度蒙皮而言，加筋比K1和厚度比K2可在一定的范围内取值，然后根据相关的加筋比和厚度比进行薄板加筋设计，完成一次设计之后，更新加筋比和厚度比，直到更新完所有取值。优化流程图如图1所示。

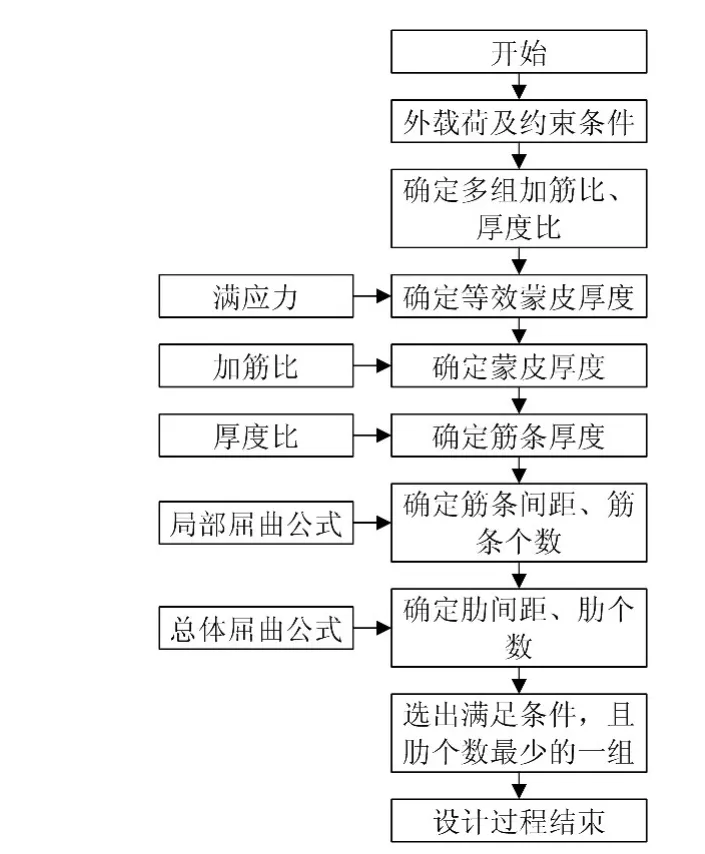
图1 加筋设计流程

接下来，利用Maple软件对上述优化流程进行编程实现，对2 000mm×1 000mm的矩形薄板结构进行加筋优化设计，加筋板四边简支，轴向压缩载荷F=1.5×106N，材料为铝合金材料，弹性模量E=70GPa，泊松比 μ =0.3，密度 ρ=2.7E －9 t/mm3，许用应力［σ］ =300MPa，将加筋比 K1和厚度比 K2的取值范围分别设置为0.4～1.0和1.1 ～1.8，计算步长都为 0.1，这样就有 56 次计算得到56组计算结果。在56组计算结果中，为了避免筋条局部失稳，滤掉筋条高度大于40mm的计算结果，选出肋个数最少且在筋条个数和肋个数取整时误差较小的一组结果。

1.4 加筋板的有限元验证

根据1.3节的优化设计流程，对2 000mm×1 000mm的轴压四边简支矩形薄板进行矩形筋条的加筋设计，得到一组最优结果为:

加筋比K1=0.7

厚度比K2=1.8

蒙皮厚度Ssk=2.94mm

筋条厚度Sst=5.29mm

筋条高度h=35.35mm

筋条间距w=100.86mm

肋间距l=505.35mm

取整后筋条个数N=11个

取整后肋个数M=3个

理论局部屈曲因子f局=1.03

理论总体屈曲因子f总=1.05

将上述结构参数在有限元软件Hyperworks中进行有限元建模［4］，为了避免薄板两端加载时的应力集中问题，对模型两端分别建立500mm×1 000mm的过渡段，建模时利用二维壳单元模拟蒙皮结构，一维梁单元模拟筋条，对于肋的模拟则通过在加筋板结构的肋位置添加相关约束来实现，并且对筋条进行0.5h的偏置处理，整个有限元模型如图2所示。

图2 常规加筋有限元模型

结构有限元分析应力云图和一阶屈曲图如图3，4 所示。

图3 常规加筋应力云图

图4 常规加筋一阶屈曲图

对结构的应力云图及一阶屈曲图分析可知，虽然在结构的两端添加了过渡段，却仍然无法完全避免两端的应力集中问题，但是结构整体上的应力还是保持在300MPa左右，由于加筋板两端的应力集中，导致在其两端首先出现蒙皮局部屈曲，加筋板的首阶蒙皮局部屈曲因子为1.03，首阶总体屈曲因子为1.04，对比优化设计的理论屈曲因子，可视为该有限元建模设计验证了1.3节加筋板优化设计方法的可行性。

2 拓扑优化薄板加筋设计

2.1 稳定性约束的基板拓扑优化

在常规的薄板加筋方法中，筋条的形式和尺寸参数一般都是相同的，筋条的分布一般也都是沿轴向均匀分布，这样就对加筋板限制了一些设计变量，如筋条在加筋板中的拓扑形式及每根筋条独立的尺寸参数。将薄板加筋结构中的筋条布局设计跟拓扑优化方法联系起来，可使结构中筋条的布局设计问题转化为基板中材料分布的问题，即在带有最小厚度限制的拓扑优化结果中根据材料分布的痕迹来加筋，得到结构效率高的加筋板结构。

下面对一块2 000mm×1 000mm的轴压四边简支矩形基板进行稳定性约束的拓扑优化，基板厚度设置为50mm，为了避免应力集中的问题，对基板两端分别建立500mm×1 000mm的过渡段，模型中板壳结构均用二维单元模拟，网格尺寸为20mm，有限元模型如图5所示。

图5 拓扑优化基板有限元模型

对上述有限元模型进行以设计区域体积最小为目标、薄板屈曲因子大于1.00为约束条件的拓扑优化，并设置基板最小厚度为30mm，其中中间矩形基板为设计区域，设计区域的拓扑优化结果如图6所示。

图6 基板的拓扑优化结果

2.2 基于拓扑优化结果的薄板加筋效果

由图6可知，深色区域的薄板厚度为3mm，浅色区域的薄板厚度为50mm，介于深色和浅色之间的区域厚度在3～50mm之间。至此，可根据材料分布的痕迹来对薄板进行加筋，这样就把薄板筋条分布的问题转化为了基板中材料分布的问题。根据2.1节的拓扑优化结果，对本文1节中的薄板进行指导加筋，由于拓扑优化结果中的材料分布痕迹密度各不相同，可设置5类截面形式相同但截面尺寸不同的筋条，筋条截面形式为矩形，加筋结果如图7所示。

图7 拓扑优化加筋有限元模型

2.3 拓扑加筋结果的二级尺寸优化

在2.2节中，根据基板拓扑优化的结果，对薄板进行了筋条布局的设计，完成了拓扑优化方法指导薄板加筋的过程，并对其中的筋条按尺寸大小分成了5类。接下来根据该加筋结果，对薄板结构进行尺寸优化，在保证结构稳定性的前提下，优化蒙皮及各类筋条的相关尺寸，使得结构质量最小。

在尺寸优化过程中，目标函数为结构体积最小，约束条件为薄板屈曲因子大于1.00，设计变量分别是蒙皮厚度tsk0、5类筋条厚度tsti及高度hi，其中i=1，2，…，5。该尺寸优化过程中设计变量的初始值、上下限以及优化结果见表1。

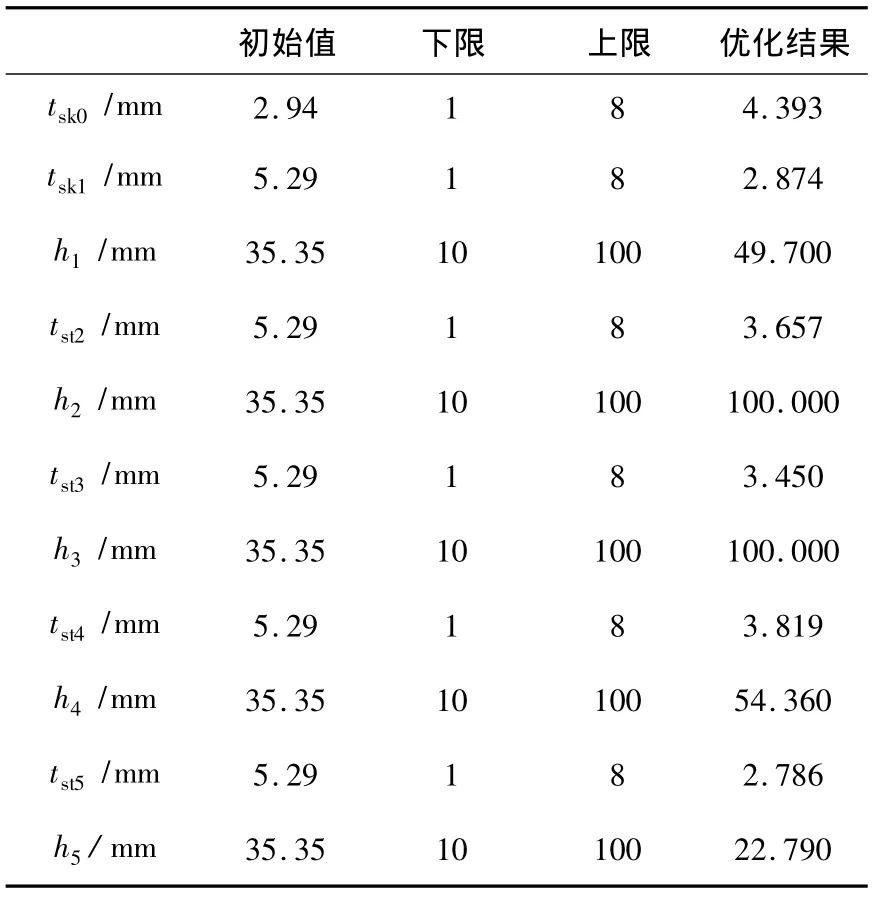
表1 拓扑优化加筋结构中的尺寸优化结果

尺寸优化后的结构满足屈曲因子大于1.00的设计要求，且每类筋条尺寸的大小能够跟拓扑优化结果中材料痕迹的疏密相吻合，加筋板总质量为3.29E－2t，结构有限元分析应力云图和一阶屈曲图如图8，9所示。

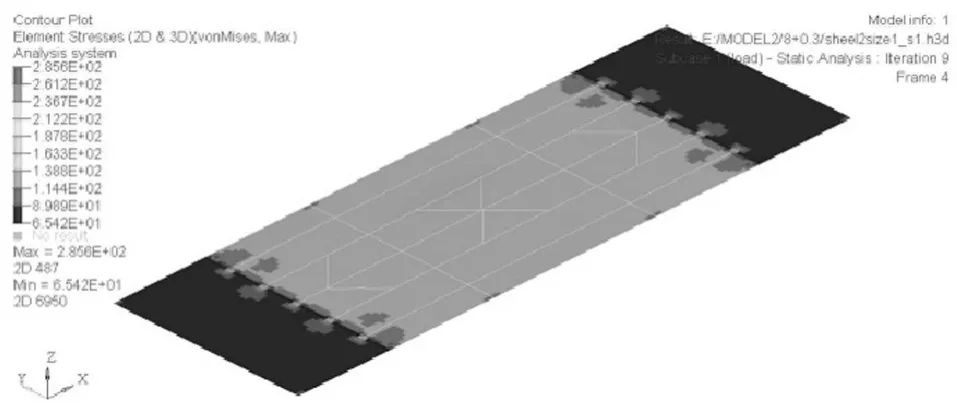
图8 拓扑优化加筋应力云图

图9 拓扑优化加筋一阶屈曲图

对结构的应力云图及一阶屈曲图分析可知，虽然在结构的两端添加了过渡段，还是无法完全避免两端的应力集中问题，但是结构整体上的应力还是保持在220MPa左右，由于该加筋板结构没有进行加肋，导致其容易首先发生总体屈曲，加筋板的首阶总体屈曲因子为1.00，首阶蒙皮局部屈曲因子为1.01，满足设计要求。

3 两种加筋方法的对比

本文中通过两种加筋方法得到的加筋板结构都能够满足设计要求。常规的加筋方法通过等效蒙皮的满应力设计，使蒙皮和筋条的平均应力控制在300MPa左右，保证了材料的利用率，但是为了满足总体屈曲要求，在该结构中还需要进行加肋，每个肋高度假设为薄板宽度的1/4，考虑到连接件等因素，肋板的平均厚度假设为蒙皮厚度的1.5倍，3个肋总质量为8.93E－3t，再加上等效厚度蒙皮的质量2.7E－2t，整个结构总质量是3.59E－2t。

拓扑优化指导加筋的方法中，由于不需要进行加肋，就使得肋材料可以分一部分到蒙皮/筋条结构中去，对筋条布局完成以后的加筋板结构进行尺寸优化，能够得到满足设计要求的加筋板结构，并且蒙皮和筋条的平均应力在220MPa左右，为满足总体屈曲的要求，导致筋条高度相对比较高，因此要注意筋条失稳的问题，整个加筋板结构总质量是3.29E －2t。

4 结束语

对于常规加筋方法而言，其设计思路清晰，加筋流程简单，但是对加筋比K1和厚度比K2的选取具有一定的随意性，依赖于设计人员的工程经验，本文通过编程实现最优加筋比和厚度比的选取。

通过对基板的拓扑优化，在一定程度上能够得到合理的加筋痕迹，将筋条布局设计问题转化为基板材料分布问题，设计变量更加多样化。

为了保证加筋板的总体屈曲要求，常规加筋方法通常需要加肋，容易导致材料的浪费，拓扑优化指导加筋的方法不需要加肋，但筋条高度较高，容易产生筋条失稳。

本文中分别通过两种加筋方法得到的加筋板结构，相对于常规加筋方法，拓扑优化指导加筋的方法达到了减重8.4%的效果。

［1］ Bendsoe M P.Sigmund O.Topology optimization;theory，methods and applications［M］.New York:Springer Verlag Berlin Heidelberg，2002.

［2］ 赵群.复合材料翼面结构布局优化设计方法研究［D］.南京:南京航空航天大学，2010.

［3］ 王志瑾，姚卫星.飞机结构设计［M］.北京:国防工业出版社，2011.

［4］ 洪清泉，赵康，张攀，等.OptiStruct＆HyperStudy理论基础与工程应用［M］.北京:机械工业出版社，2012.