下肢外骨骼机器人人机约束模型建立及分析

段启超，赫东峰，刘 波，张君安

(西安工业大学机电工程学院，陕西西安 710021)

外骨骼机器人是一种可以让人直接穿戴的动力机械智能设备，它将人的智能与机器人的“体力”结合在一起，以人的智力控制为主导，结合机器人的动力设备来增强人体的防御、行走、负重等生理机能，进而提高使用者的作业能力［1］。其中下肢助行外骨骼机器人用于辅助正常人的行走、跑步、登山等运动，提高人们行走的能力和速度，缓解人在大负重和长时间行走的情况下极易出现的疲劳感。因此，下肢外骨骼机器人在军事、科考、旅游、交通、救灾等各方面，具有广泛的应用前景［2］。

人体外骨骼机器人作为一种可穿戴型机构，人与机构之间的相互作用尤为重要，目前对于人机约束的研究还比较缺乏。人机约束设计直接影响穿戴舒适性和运动特性。人机约束指的是穿戴的连接模型，是关联人机运动的重要形式。若人机约束机构选取合理，可以使人机系统运动协调，保证穿戴紧凑。约束选取不合理会造成对应运动的失效，例如:约束过度，人机运动会出现干涉;约束不足，运动中人机对应运动副偏移而使人机不协调，运动难以预测［3－4］。人机约束的选取要求是，在保证机构可运动的前提下，使人体骨骼运动较好地跟随外骨骼机构运动。

1 助力外骨骼机器人机构设计

本文设计的人体外骨骼机器人共有6个自由度，其中髋关节具有3个自由度，分别为髋关节的屈伸、内摆外摆、内旋外旋，膝关节具有1个屈伸自由度，踝关节具有屈伸与内摆外摆2个自由度。髋关节的屈伸与膝关节的屈伸为主动自由度，由液压缸控制运动，其余4个自由度为被动关节［5］。总体机构设计方案和三维模型如图1所示。

图1 下肢外骨骼机器人机构设计

2 约束方案

人机系统简图如图2所示。

图中A、B、C分别代表了人体髋关节、膝关节与踝关节，其中髋关节与踝关节简化为球轴，膝关节简化为一个转动副。D、E、F、G、H、I分别代表外骨骼机器人的髋关节内摆外摆、屈伸、内旋外旋关节、膝关节屈伸关节、踝关节内旋外旋和屈伸关节，这些关节全部为转动副。虚线ab与cd表示待确定的人机系统约束［6］。

图2 人机系统简图

3 运动学模型建立及计算约束方程

针对2种不同约束方案，下面分别求解其人机约束方程。

本文提出了2种不同的约束方案，如图3所示。

图3 约束方案

依据D－H方法建立如图4所示的坐标系［7］。人体髋关节球轴所在坐标系O0－X0Y0Z0为不变坐标系。

图4 D－H运动学坐标系

首先建立各方案腿部连接的约束方程。

方案一:由D－H变换阵可得，从人体髋关节球轴的坐标系原点O0到大腿约束点O10的齐次变换为:

式中:s表示三角函数sin;c表示三角函数cos;α为坐标系x方向的角度变化量;β为坐标系y方向的角度变化量;γ为坐标系z方向的角度变化量。

从人体髋关节球轴的坐标系原点O0到大腿约束点O的齐次变换为:

根据O10与O点坐标相同可以得到约束方程:

同理，方案二:由D－H变换阵可得，从人体髋关节球轴的坐标系原点O0到大腿约束点O13的齐次变换为:

从人体髋关节球轴的坐标系原点O0到大腿约束点的齐次变换为:

根据O13与O点坐标相同可以得到约束方程:

4 约束方案检验

由上述约束方程分析不同人机约束方案下人机系统的跟随效果。为便于研究，分别假设人体仅沿一个自由度运动，其他自由度保持在原点不动，然后通过约束方程求解外骨骼机器人对人体的跟随情况［8］。

方案一:

a.假设 γ0，γ2未知，其余角度均为0。将f1，f2，f3化简可得

将l3+l13=l15带入式(7)可得

由此可知，γ0与γ2在运动过程中时刻相等，满足运动要求。

b.假设 α0，γ1未知，其余角度均为 0。将 f1，f2，f3化简可得

将l2=l0带入式(8)可得

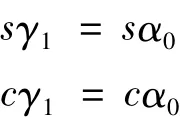
由此可知，γ1与α0在运动过程中时刻相等，满足运动要求。

c.假设 β0，γ3未知，其余角度均为0。将f1，f2，f3化简可得

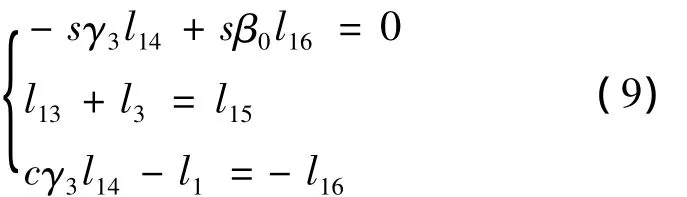
将 l3+l13=l15，l14=l16，带入式(9)可得

由此可知，γ3为确定值，表示这个运动副不能转动，不满足运动要求。

方案二:

a.假设 γ0，γ2未知，其余角度均为0。将f4，f5，f6化简可得

将 l2=l0，l3+l13=l15，l16=l17带入式(10)可得

由此可知，γ0与γ2在运动过程中时刻相等，满足运动要求。

b.假设 α0，γ1未知，其余角度均为 0。将 f4，f5，f6化简可得

将 l2=l0，l3+l13=l15，l16=l17，2l14=l1带入式(11)可得

由此可知，γ1与α0在运动过程中时刻相等，满足运动要求。

c.假设 β0，γ3未知，其余角度均为0。将f4，f5，f6化简可得

通过模型可知 γ11= － γ3，γ12= － β0，将 l2=l0，l3+l13=l15，l16=l17，2l14=l1带入式(12)可得

由此可知，γ3与β0在运动过程中时刻相等，满足运动要求。

通过计算可知，方案一虽然自由度满足要求，但在实际运动中人体与外骨骼机器人胯关节的内旋外旋不能转动，不满足运动要求。方案二可以满足人体与外骨骼机器人的运动要求，并且可以同步运动，满足设计初衷。

踝关节与胯关节运动类似，运用相同检验方法检验后发现，方案一中的踝关节的约束可以满足踝关节的运动要求，但不能满足胯关节的内旋与外旋。方案二可以满足人体与外骨骼机器人的运动要求。

因此，在实际穿戴时应选用方案二的约束条件对人体与外骨骼进行连接。

5 结束语

由于人体外骨骼机器人是一种穿戴型机构，因此对于人体与机构之间的相对作用与相互约束关系的研究尤为重要。而现有文献关于这方面的研究还很欠缺。本文利用D－H方法，建立了人机系统约束方程，通过约束方程求解了人体对外骨骼机器人的跟随情况，证明了通过合理设计人机系统方案，可以实现下肢外骨骼机器人对人体运动的同步跟随。

［1］ 柴虎.下肢外骨骼跟随系统的研究［D］.广州:南方医科大学，2013:1－3.

［2］ 刘会勇，赵青.下肢外骨骼助行机器人研究现状及发展趋势［J］.机械设计与制造，2013(8):146 －148.

［3］ 尹君茂.穿戴式下肢外骨骼机构设计与分析［D］.北京:北京工业大学，2010:1－37.

［4］ 刘宏伟.空间并联机构的自由度分析［J］.机械传动，2009(4):90－92.

［5］ 唐志勇，谭振中，裴忠才.下肢外骨骼机器人动力学分析与设计［J］.系统仿真学报，2013(6):1338－1344.

［6］ Andrew Chu，Kazerooni H，Adam Zoss.On the mechanical design of the berkeley lower extremity exoskeleton(BLEEX)［C］//IEEE/RSJInternational Conference on Intelligent Robots and Systems Conference，August，2 － 6，2005，Edmunton.New York:IEEE，2005:3132－3139.

［7］ 赵彦峻，徐诚.人体下肢外骨骼设计与仿真分析［J］.系统仿真学报，2008(17):4756 －4759.

［8］ Karen N，Gregorczyk H，Leif Hasselquist，et al.Effects of a lower－body exoskeleton device on metabolic cost and gait biomechanics during load carriage［J］.Ergonomics，2010，53(10):1263－1275.