对液晶受压产生变色现象的探究

郑智武，陈孔韬，郭建波，高文莉，龚国斌

(南京大学 物理学院，江苏 南京210046)

1 扭曲向列型液晶的工作原理

液晶是一种区别于固态、液态和气态的物质状态，因其同时具备晶体和液态物质的性质而得名.对于液晶分子的排列，一般可以分为3类：近晶相、胆淄相和向列相[1].本文所指“液晶”为向列相液晶，其中最为著名的是扭曲向列(TN)型液晶，其结构如图1[2]所示.在2块玻璃板之间夹有向列相液晶，玻璃板的内表面涂有透明电极，电极的表面预先作了定向处理(在电极表面涂取向剂，然后用软绒布向某方向摩擦).这样，液晶分子在透明电极表面就会躺倒在摩擦所形成的微沟槽里，上下电极上的定向方向相互垂直.由于范德瓦尔斯力的作用，从俯视方向看，液晶分子的排列从上电极的沿－45°方向排列逐步地、均匀地扭曲到下电极的沿＋45°方向排列，整体扭曲了90°.理论分析和实验结果证明[3]，上述结构具有光波导的性质，偏振光从上电极表面透过扭曲排列起来的液晶传播到下电极表面时，偏振方向会旋转90°.本文主要通过实验和理论定量分析了在白光照射下的扭曲向列型液晶在电场、外加力场作用下的变色现象.

图1 扭曲向列 (TN)型液晶的工作原理

2 理论分析

对于每束正入射的单色光束，在进入液晶时，因双折射现象分成o光和e光2束速度不同的光，在出射时经由检偏器投影到同一方向上发生干涉，产生光强不均匀分布.不同波长的正入射的单色光束，其出射光强的改变不同，所以出射光的频谱与入射光不同，混合后出现不同颜色.

由弹性力学可以建立液晶分子的偏转角度θ与压力F之间的关系.以图1中电场方向(即光轴方向)为x轴建立坐标系.设液晶器件的底面积为S，厚度为d，偏转和压缩弹性系数分别为K和k，则拉格朗日量为

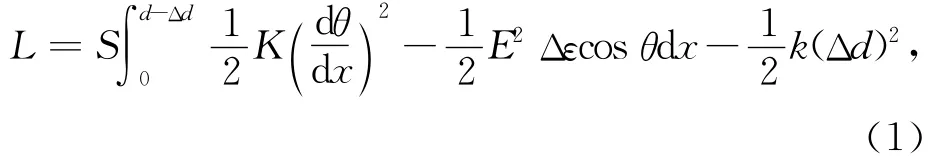
代入拉格朗日方程，解得[4]

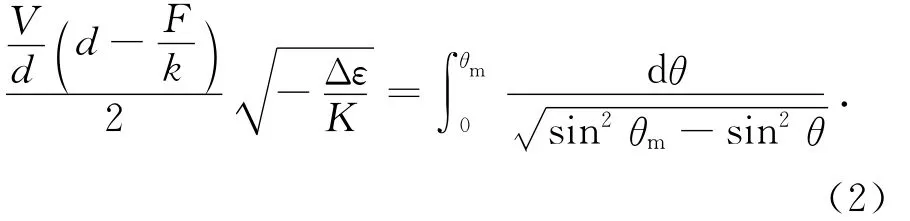
右边是椭圆积分，θm为θ最大值，取二阶级数解[4]：

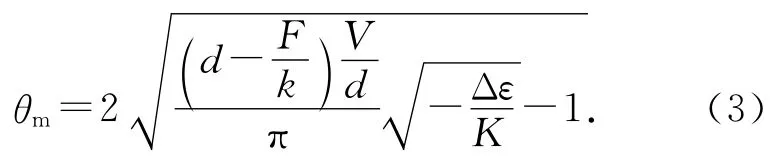
显然，θm为实数，所以方程(3)外层根号中量非负.外层根号中量恰为0时，临界电压

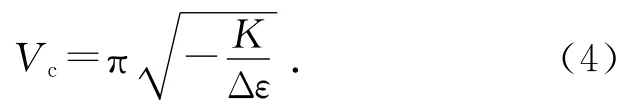
而在晶体中由麦克斯韦方程组可得[1]

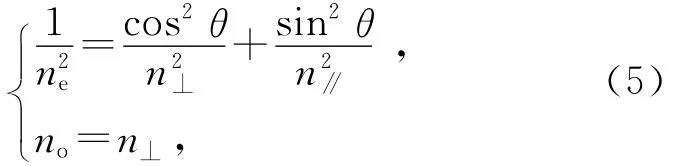
其中，ne是e光折射率，no是o光折射率，n∥和n⊥分别为平行于光轴、垂直于光轴方向的折射率.在小角近似下可认为

从而有

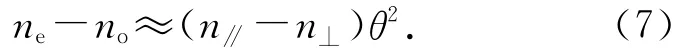
对扭曲向列型液晶

所以

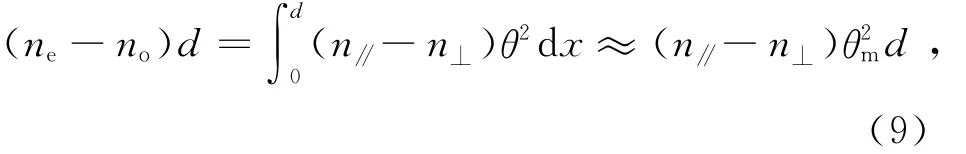
双折射的一般方程[4]为

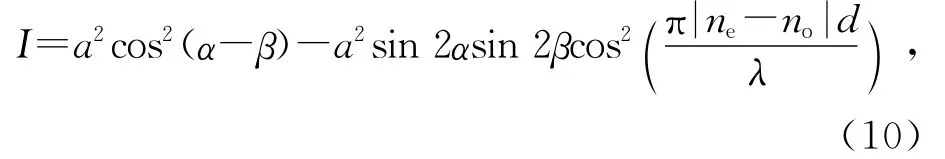
其中，a是电场振幅，α和β是晶体光轴与入射光路夹角，λ是入射光波长.实验中

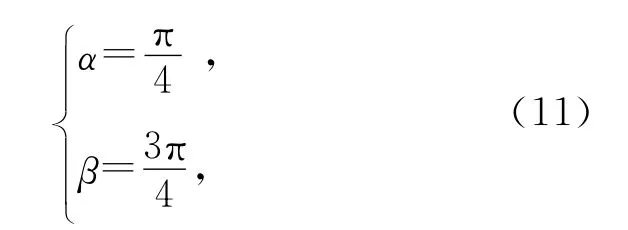
将(11)代入方程(10)有

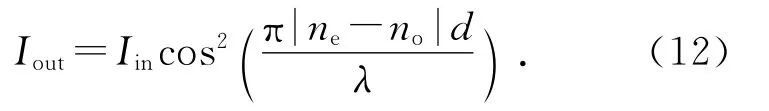
为了研究颜色的变化，引入色坐标进行分析.色度学中[5]，记

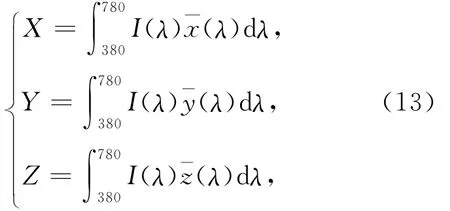
则色坐标为

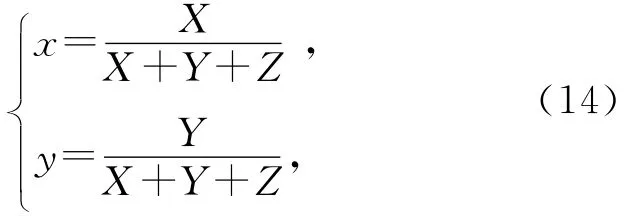
其中I为光强和是色刺激函数.x和y是CIE色坐标，用来确定混合后的颜色.由方程（3），（9），（12）～（14）得

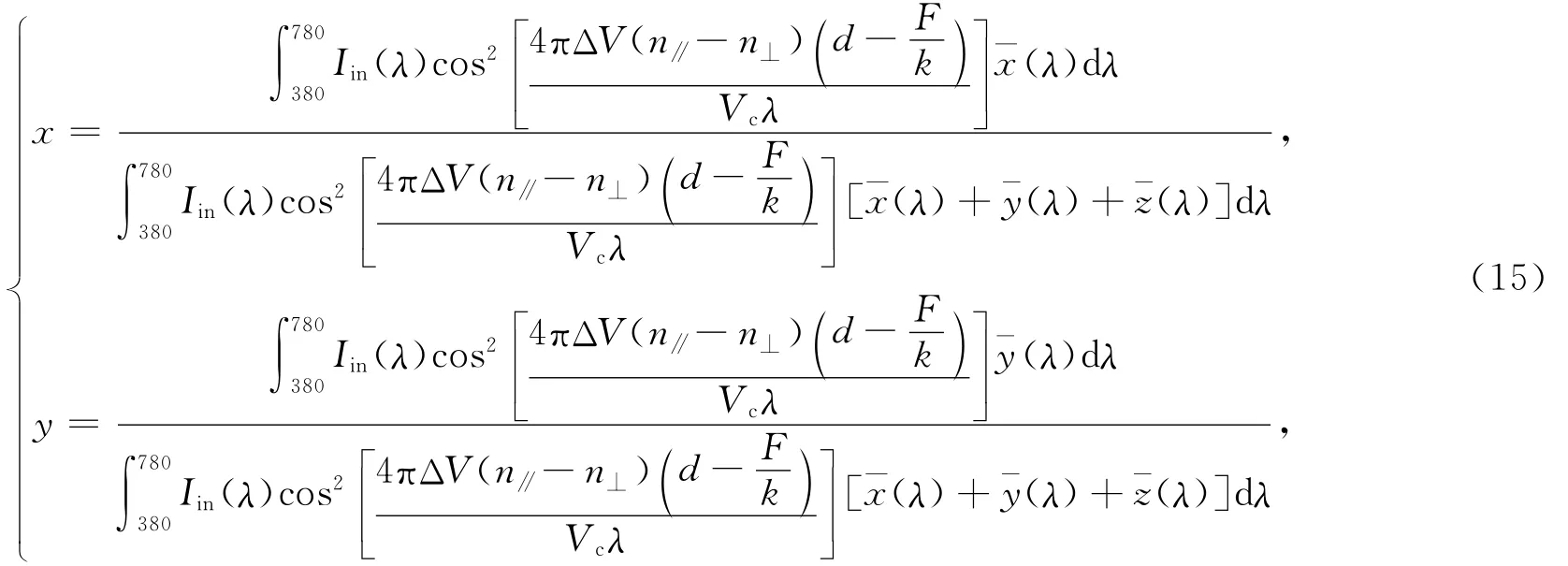
但限于实验条件，n∥，n⊥和k均无法测量，将其设为待定常量，即令

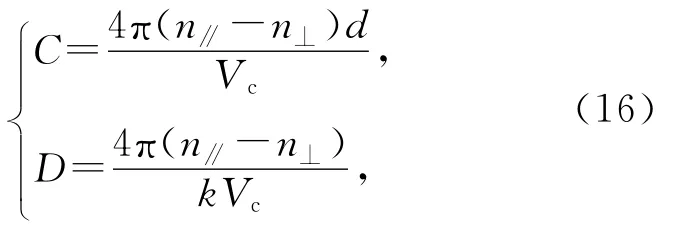
故有

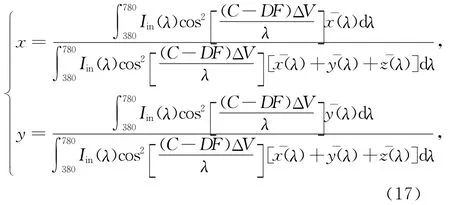
其中常量C和D可由实验测定，则方程(12)可以变为

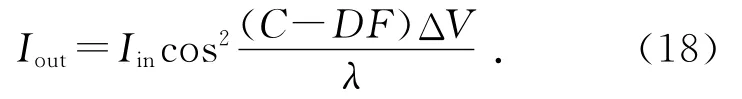
实验中把测得的单色光数据代入方程(18)来拟合C和D.

3 实验内容与数据处理

3.1 光谱测量

图2为实验光路图，偏振片虚线方向为透光方向.当光经过起偏器变成线偏振光后，入射到液晶中，出射后经过检偏器进入CCD，检偏器和起偏器的偏振化方向正交，用CCD来感知光的颜色和相对光强信息.实验中使用了12张滤波片，以得到不同波长的单色光，通过CCD捕捉光强信息，近似得到入射光光谱.

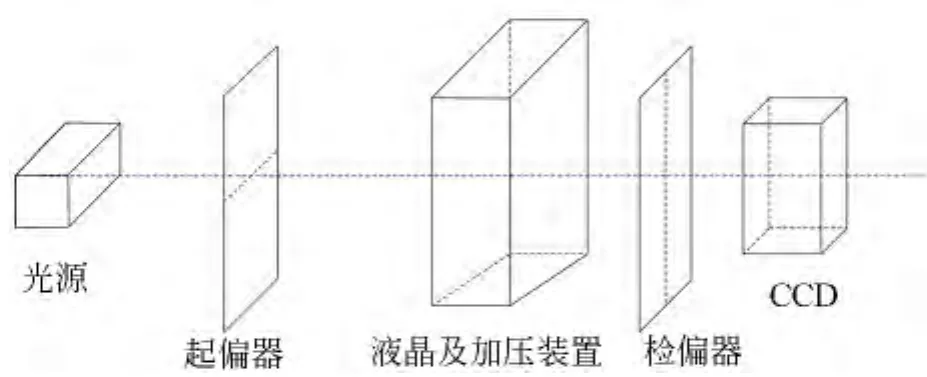
图2 实验光路图

根据CIE 1931RGB色度系统中三原色红、绿、蓝分别对应的波长为：λR＝700nm，λG＝546nm，λB＝435.8nm，每个像素点的R，G，B值可以认为是为了获得这个像素点的颜色3种光需要入射的相对强度，所以使用如下公式进行计算：

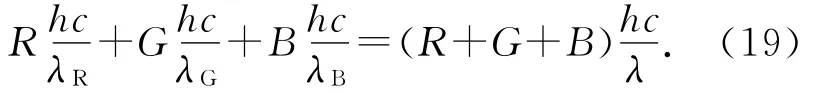
为验证式(19)的合理性，使用1张拍摄的液晶照片，用基于式(19)的Java程序进行处理，得到每个像素点的平均波长和相对强度值，由单色光的波长和其强度可以知道对应颜色的R＋G＋B值，这样再反过来利用这个值用Java程序进行画图，把该图(图4)与处理前的照片(图3)进行对比，可以知道这种处理方法是合理的.

图3 原始液晶照片

图4 用Java程序处理后得到的液晶照片

通过12张经过滤波片的入射光照片，用上述程序得到图片每个像素点的R，G，B值，由此得到对应的相对光强.为了计算方便，把所有像素点的光强进行平均，并将其作为该单色光的强度，这样可以得到12个波长的光对应的相对强度值，使用样条插值[7]拟合出入射光的光谱(图5).

3.2 C和D值拟合

实验使用λ＝480nm的滤波片，得到单色光，保持拍摄电压4.0V不变(液晶的临界电压Vc＝3.1V)，改变外界压力，通过CCD捕捉得到在不同压力下液晶的照片，经程序处理得到出射光的相对光强Iout，再在无液晶情况下拍摄照片，

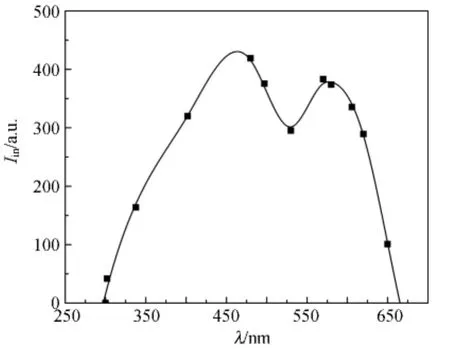
图5 入射光相对强度测量与插值曲线

得到入射光的相对光强Iin，即利用(18)式得到：

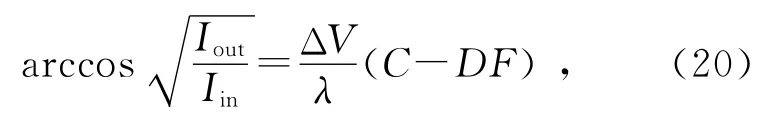
拟合结果如图6所示.得到：

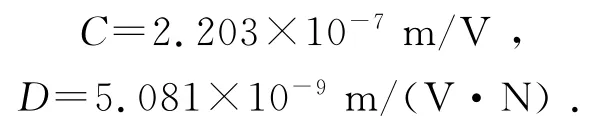
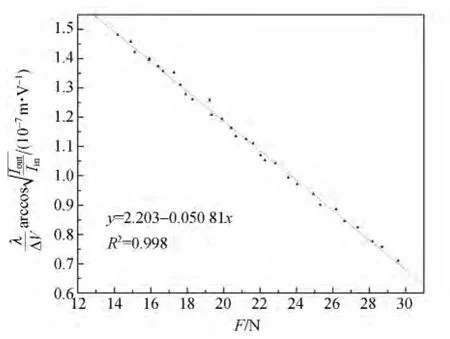
图6 拟合常量C和D

3.3 白光入射下的实验与理论对比

用白光入射，拍摄不同压力下（固定电压）和不同电压下（固定压力）的照片，将每张照片的R，G，B值进行平均，得到，通过RGB空间与XYZ空间的变换公式，结合式（14）便可计算色度（x，y），这 样得到 （x，F），（y，F），（x，ΔV），（y，ΔV）的散点图.在理论方面，通过将3.1中光谱的插值函数代入式（17），拟合得到液晶的颜色随电压、压力的变化关系 （图7）.

在只改变压力(固定电压4.9V)或电压(固定压力0)的情况下可以获得与实验相对应的理论曲线图.将测量数据与理论图画在同一张图上进行对比(如图8～9所示)，可见，理论和实验结果一致.

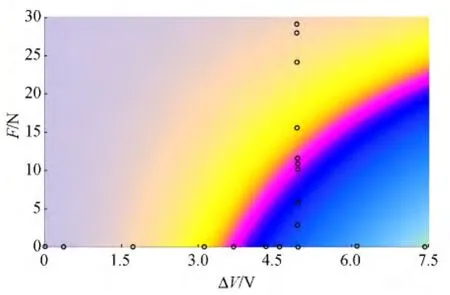
图7 液晶颜色与电压、压力关系(图中黑圆圈代表实验测量的点)

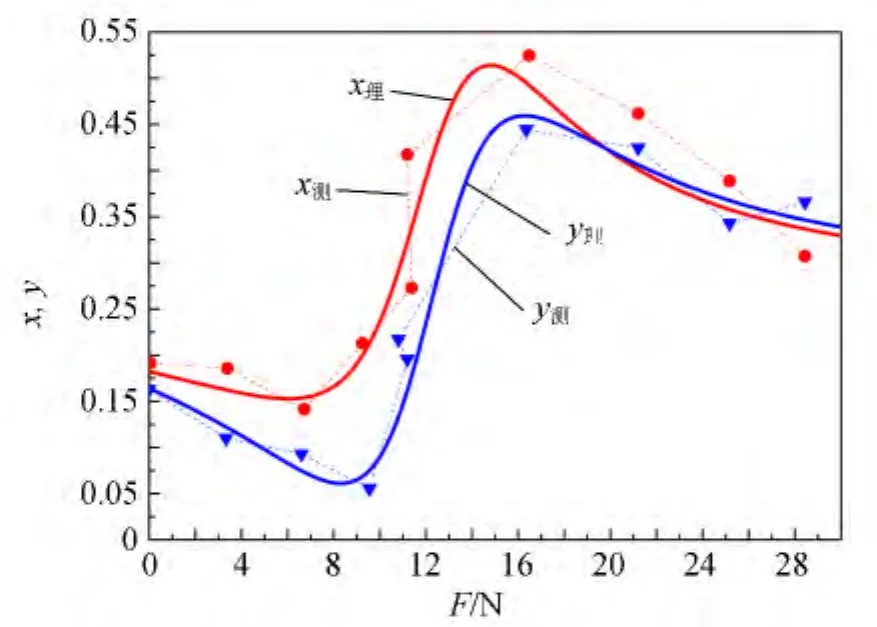
图8 色坐标分量x，y与所加压力F的关系曲线

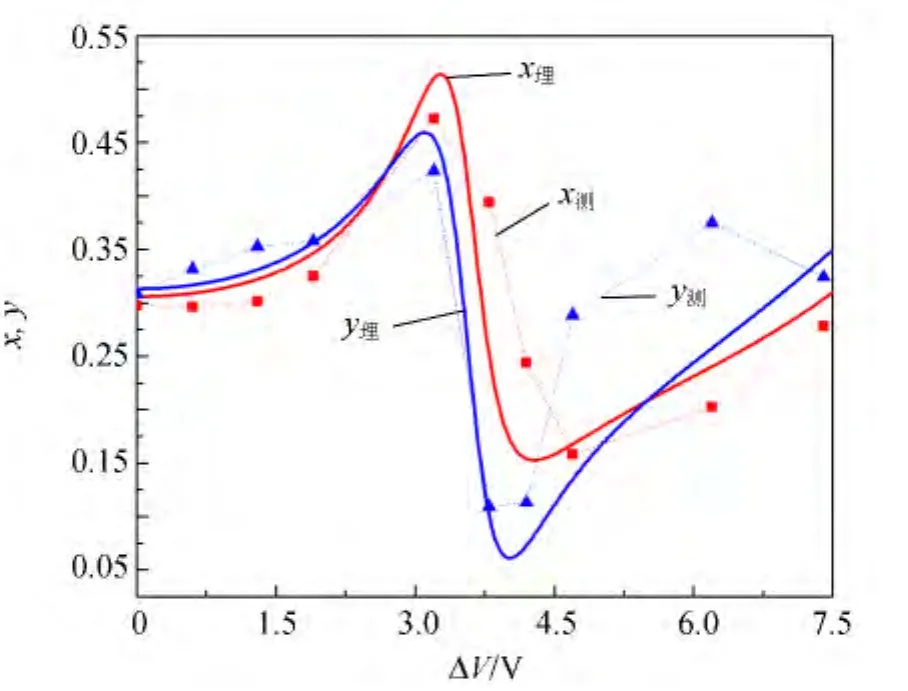
图9 色坐标分量x，y与所加电压ΔV的关系曲线

4 结 论

光入射液晶后，分为o光和e光进行传播，出射后透过检偏器投影到同一方向上发生干涉.由于不同波长成分的光的o光和e光部分产生的相位差不同，干涉之后的出射光强也就不同，所以出射光强较入射光强在成分上发生了变化，造成了颜色的变化.经过定量的理论和实验的分析，发现在电压逐渐加大时，液晶颜色按照黄色、红色、蓝色的趋势变化；在压力逐渐加大时，液晶颜色按照蓝色、红色、黄色的趋势变化.实验结果和理论分析一致.液晶的这一性质在压力传感器、显示屏等领域有应用前景，具有灵敏度高，响应时间短，能够一定程度上分辨压力作用点等特点.

[1]Chandrasekhar S.Liquid crystals[M]2nd ed.Cambridge：Cambridge University Press，1992.

[2]魏向东.聚合物分散液晶的压光效应研究[D].天津：河北工业大学，2010.

[3]de Gennes P G，Prost J.The physics of liquid crystals[M].Oxford：Clarendon Press，1993.

[4]黄子强.液晶显示原理[M].北京：国防工业出版社，2002.

[5]顺青.色度学[M].北京：北京理工大学出版社，1990.

[6]CIE(1932)[C]//Commission internationale de I’Eclairage proceedings.Cambridge：Cambridge University Press，1931.

[7]Guo Ben－yu，Wang Zhong－qing.Numerical integration based on Laguerre－Gauss inter－polation[J].Computer Methods in Applied Mechanics and Engineering，2007，96(37)：3726－3741.