折射成像问题定量研究

莫 滨，张 靖

(南京市第十八中学，江苏 南京210022)

1 折射成像

观察者从空气中向下观察水中物体时的虚像位置，有3种观点：1)像在物的上方且偏离观察者处[1]；2)像在物的上方且偏近观察者处[2]；3)像在物的正上方[3].

竖直物体成像形状的画法也不同，有仍然竖直的[4]，有图1所示倾斜的[5].

图1 人教版高中物理教材选修3－4画法

文献[6－8]从不同角度定性讨论了成像的正确位置，都采用2束折射光线反向延长线相交的方法.其中文献[8]因2束光线角度相差较大，不符合人眼的实际视域，反而得出虚像等大的错误结论.为了得到这个问题的正确结论，本文采用了适当的数学方法，确定了像点的位置与观察角的定量关系.

2 定量分析

为了得出普遍适用的定量关系，分析如图2

所示的斜射的情况.

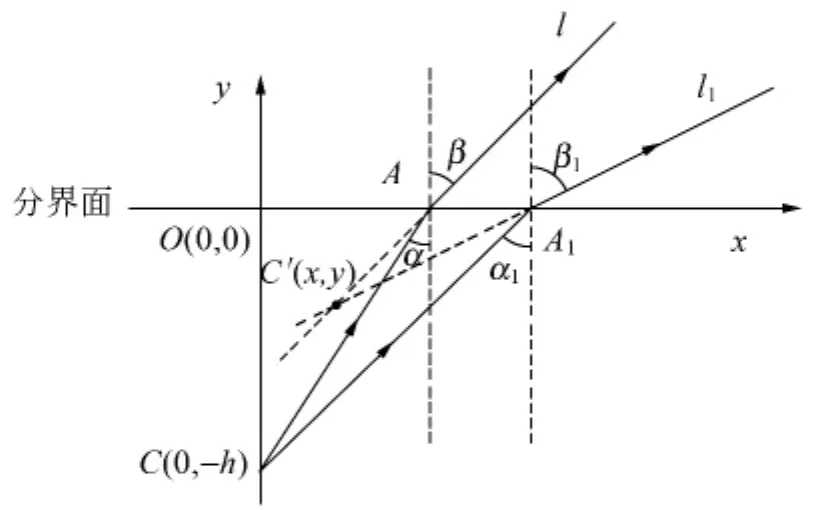
图2 观察者在光疏介质中观察光密介质物点C的成像示意图

光密介质中的物点C(0，－h)发出的光线在分界面发生折射，形成过A(htanα，0)点的折射光线l，其直线方程为

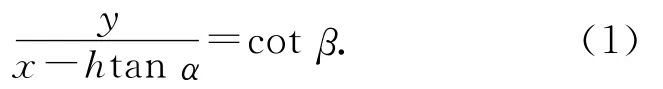
过A1(htanα1，0)点的折射光线l1，直线方程为

联立式(1)～(2)求解(x，y)，即l和l1的反向延长线交点，就是物点C(0，－h)所成的像点C′(x，y)，得

根据折射定律，β由α确定，β1由α1确定.像点C′(x，y)最终由α和α1确定.为了精确地找出像点与α的关系，用类似从运动物体平均速度求即时速度的方法，考虑函数导数的定义，令α1＝α＋Δα，由式(3)有

令图2中的相对折射率为n，则由折射方程

计算得

将式(6)代入式(1)可得

根据折射定律可写为

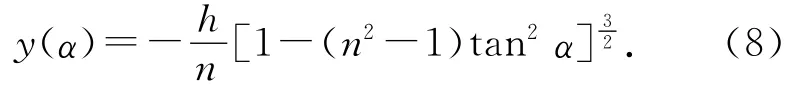
应用上述结果，用式(6)和式(8)可确定物体坐标为(0，－h)、入射角为α时，折射成像时虚像的坐标，颠覆了采用2束光线确定像点的方法.至于只需要确定区域范围的定性分析的应用实例，将具有确定性.

3 结果与讨论

研究式(6)～(7)可知，公式对光疏介质向光密介质折射时也同样成立.

1)当n＞1时，光从光密介质射向光疏介质，由式(6)，在α的取值范围内，有为临界角)，对固定的h，x(α)是α单调增函数.表示在x轴方向上，像介于物体和观察点之间，所以像变小.x(α)是α单调增函数，最大值为，所以得.

从式(7)，可知y(α)＞－h且是α的单调增函数.有，y轴方向上像变小.y的极小值就是像的极大值，这只在α＝0出现，此时物点(0，－h)对应的像点为

从而得出结论，除了(0，0)点之外的物点发出的光由光密介质进入光疏介质中，不论是在x轴和y轴方向，像都落在观察者和物体之间，可以认为像变小.如图3所示.

图3 光密介质向光疏介质折射成像位置示意图

2)当n＜1时，光是从光疏介质进入光密介质，有0≤α＜90°，从式(6)，x(α)≤0，表示在轴方向上，像变大.x(α)随α增大而单调递减.对固定的h，由于0≤tanα＜∞，所以0≥x＞－∞.

可得出结论，除了(0，0)点之外的物点发出的光由光疏介质进入光密介质中，不论是在x轴和y轴方向，像都落在观察者和物体之外，像变大，如图4所示.

图4 光疏介质向光密介质折射成像位置示意图

根据式(6)，式(7)或式(8)与上面的结论，由于像点与物点的关系，可进一步得出下列结论：

1)物体上特定点对于同一入射角α(折射角β)只在某方向上成像，即对于特定的观察者，像点唯一.

2)对于物体上的特定点，对不同的入射角，像的位置不同，大小也发生变化.

3)除了(0，0)点之外的物点发出的光由光密介质进入光疏介质中，不论是在x轴和y轴方向，像都落在观察者和物体之间，成缩小的虚像.

4)除了(0，0)点之外的物点发出的光由光疏介质进入光密介质中，不论是在x轴和y轴方向，像都落在观察者和物体之外，成放大的虚像.

4 应 用

4.1 应用1

用式(6)，式(7)或式(8)，研究从固定点(l，h1)观察位于y轴负方向重合的直线上各点(0，－h)所成像点(x，y)的情况，以折射角β为参变量，作图5.

图5 从定点观察竖直放置的物体

从定点(l，h1)处看点(0，－h)所形成的像(x，y).α为入射角，β为折射角.

从式(10)和式(11)得到，当在(l，h1)点，折射角为β时，观察到的点为(0，－h)，有

讨论如下：

1)相对折射率n＞1时，光从光密介质中的动点(0，－h)射向光疏介质中的固定观测点(l，h1)，所看到的像点为(x，y)，tanβ的取值范围为

从式(7)可以得出

所以，所有的点(0，－h)所成像都在y轴方向上向观察者移动.

从式(10)可看出，当tanβ＝0时变至时，x从0逐渐增大，又减小到0，表明x有极大值.

如果是从岸上看水中沿y轴负方向的直线，均取现给出2个例子：1)l＝1，h＝10；

图6 当的像

图7的像

2)l＝10，h1＝10.采用Excel软件，绘制图像，如图6～7所示.

2)相对折射率n＜1时，光从光疏介质中的动点(0，－h)射向光密介质中的固定观测点(l，h1)，所看到的像点为(x，y)，设临界角为θ0，只能在0≤β≤θ0的范围内接收到折射光.因为，取α＝90°，sinα＝0，则β＝θ0，

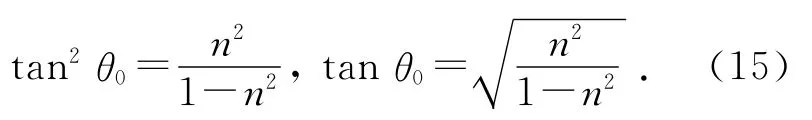
注意：此处临界角的正切的表达形式和前面的表达是不同的，原因在于，临界角总是位于光密介质中.下面分3种情况论述：

图8

2)情况2.即观察角最大值等于临界角，讨论略去.物体的像的图形与情况(1)中相似.

3)情况3.即观察角最大值大于临界角，情况更复杂，讨论略去.仅给出，由软件得到的像(x，y)的图像，见图10.

图9 当时的像

图10的像

由此看出，从定点观察垂直分界面的直线物体折射时的虚像，是一条有极值点的曲线.如果从定点观察不同介质中一般物体的图像，实际上非常复杂.

4.2 应用2

如图11，由水下点A处发出的光以30°入射角射出水面，求该点像的位置.

定量法：直接用式(6)和(8)计算，得出A′的坐标为(1.497，－4.781)，见图11.

图11 计算所得像点

作图法：取2束入射光线，粗略地画出其折射光线，作反向延长线，得其交点，即为像点，由于折射光线的取法不同，可以得到不同的结果，见图12和13，差别很大.如要精确，则计算远比公式法复杂.

图12 作图法所得错误像点1

图13 作图法所得错误像点2

5 结 论

用定量的方法，对物体在光的折射现象中形成的虚像进行讨论后发现，即使最基本的直线所成的图像，都十分的复杂，一般物体在光的折射中所成的虚像就更加复杂，只能由计算机用定量的方法去完成.对有限物体，从光疏介质中某固定观察点看光密介质中的物体时，应采用文献[2]的画法；从光密介质中某固定观察点看光疏介质中的物体时，例如图1，建议修正为图14.

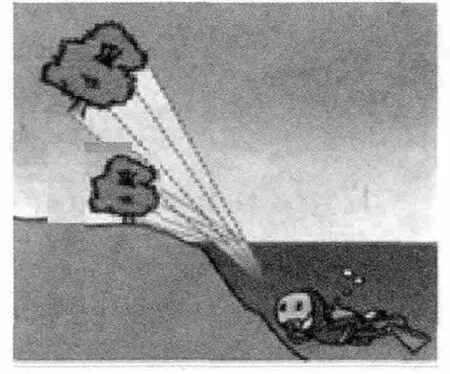
图14 对图1的修正

[1]苏科版初中物理教材编写组.义务教育课程标准实验教科书·物理教师教学用书(8年级上册)[M].南京：江苏科学技术出版社，2007：123.

[2]闫金铎.义务教育教科书·物理(8年级上册)[M].2版.北京：北京师范大学出版社，2013：113.

[3]陈熙谋，吴祖仁.普通高中课程标准实验教科书·物理(选修3－4)[M].北京：教育科学出版社，2006：62.

[4]人民教育出版社课程教材研究所.义务教育教科书·物理(8年级上册)[M].北京：人民教育出版社，2012：82.

[5]人民教育出版社课程教材研究所.普通高中课程标准实验教科书·物理(选修3－4)[M].3版.北京：人民教育出版社，2010：50.

[6]汪海涛.水中观像位置的数学推导[J].物理通报，2004(4)：6－7.

[7]王忠云.光的折射成像位置究竟应该在哪里？[J].物理教师，2004，25(8)：35，38.

[8]周美建.几何光学中成像性质的确定[J].物理通报，2014(3)：61－64.

[9]杨燕婷，邵温怡，金戈.自制光的全反射演示仪[J].物理实验，2014，34(9)：20－21.