转动惯量测试仪的设计

谢 亮，张进治，安艳伟，铁小匀

(北方工业大学 理学院，北京100144)

转动惯量是刚体绕定轴转动时转动惯性大小的量度，是刚体运动学中重要的物理量，而且在机械制造、军事航空、船舶建造等领域都有所涉及，因而，转动惯量的计算与测量一直是大学物理教学与实验中必不可少的内容[1－2].对形状规则、质量均匀分布的刚体转动惯量可直接计算得到，但是对于形状不规则、质量非均匀分布的刚体，其转动惯量只能通过实验测量得到.目前常用的实验测量方法主要有：三线摆法、扭摆法、复摆法等[3－5].经过分析发现，这些方法有的测量速度较慢，有的实验原理与转动惯量的理论原理联系不紧密，有的测量手段较陈旧，学生难以学到现代的测量技术.近年，由于计算机技术与单片机技术的发展，一些新的测量方法得以出现[6－7].受此启发，笔者根据复摆测量转动惯量的原理，设计了测量不规则刚体转动惯量的装置，加入了现代化的测量手段，具有测量方便、速度快、实验原理与理论联系密切、智能化程度高等优点.

1 装置的测量思路

本文介绍的转动惯量测试仪利用平行轴定理进行测量，即刚体绕某个转轴的转动惯量J等于刚体绕过质心平行于该轴的转动惯量Jc加上刚体质量m乘以两轴间距离d的平方.故刚体绕通过其质心且平行于已知转轴的转动惯量为Jc＝J－md2.

2 实验装置结构

实验装置结构如图1所示.2个同厂家同型号的废旧物理天平的底座平行放置，底座上方的刀口处安置水平转轴；长方体的转动惯量架与物理天平游码标尺支架固定在一起，其中心的圆孔穿过转轴使得整个转动惯量架可绕转轴自由摆动，摩擦较小；对射式光电计数器可以测量装置的摆动周期，测量精度为0.001s，10个摆动周期计数1次；倾角传感器可以测量转动惯量架相对于水平面的倾角，测量精度为0.01°；压力传感器安装于长方体转动惯量架的一个棱边的中央，如图1所示，可以测量施加给转动惯量架的压力F，测量精度为0.01g.该压力传感器为电阻应变式传感器，只要对其施加压力，其悬臂会发生形变导致其阻值发生变化，阻值的变化量经由电桥电路转化为电压信号，电压信号经过输出并放大，经由单片机转换成数字信号并乘以对应的转化系数，即可得到压力的实际大小，其具体数值可由液晶显示器显示.故给转动惯量架施加压力F时，只要用手指给压力传感器施加外力即可.测量得到的周期、角度、压力的具体数据经51单片机收集由LCD1602液晶显示屏显示.

测量时首先测出转动惯量架空载时绕水平转轴的转动惯量J1，再将被测刚体放入转动惯量架内，测出刚体的重心位置Zc以及总转动惯量J2，根据平行轴定理即可得到刚体绕通过其重心且平行于水平转轴的转动惯量Jc.需要说明的是，J1，J2和Jc的具体测量结果都经过单片机处理并由液晶显示屏显示.

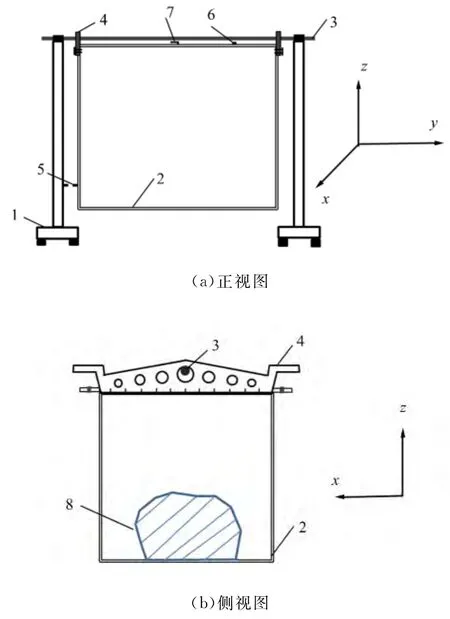
图1 实验装置结构图

3 测量原理

实验装置测量原理图如图2所示，H为转动惯量架的高度，D为转动惯量架的重心位置，ZD为转动惯量架重心距基线的高度，C为刚体的重心位置，ZC为刚体重心距基线的高度，a为F的作用点至转轴的距离.

3.1 刚体重力的测量

为了提高测量精度，采用2个称重传感器进行测量.若刚体的重力为GC，2个称重传感器测出的值为G1和G2，则：GC＝G1＋G2.

3.2 刚体Z方向重心位置的测量

首先不放刚体.调节物理天平底座上的水准仪使仪器处于水平位置，并使得转轴3处于水平位置，调节平衡螺母使得转动惯量架左右对称，倾角传感器示数为零.让转动惯量架在外力F1的作用下发生微小偏转，偏转角为θ1，转动惯量架的重力为GD.由力矩平衡原理可知F1acosθ1＝GD(H－ZD)sinθ1，得到转动惯量架重心距底基线的高度ZD为

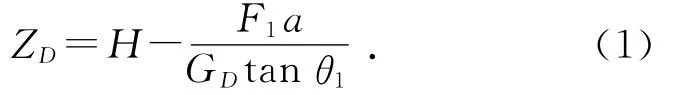
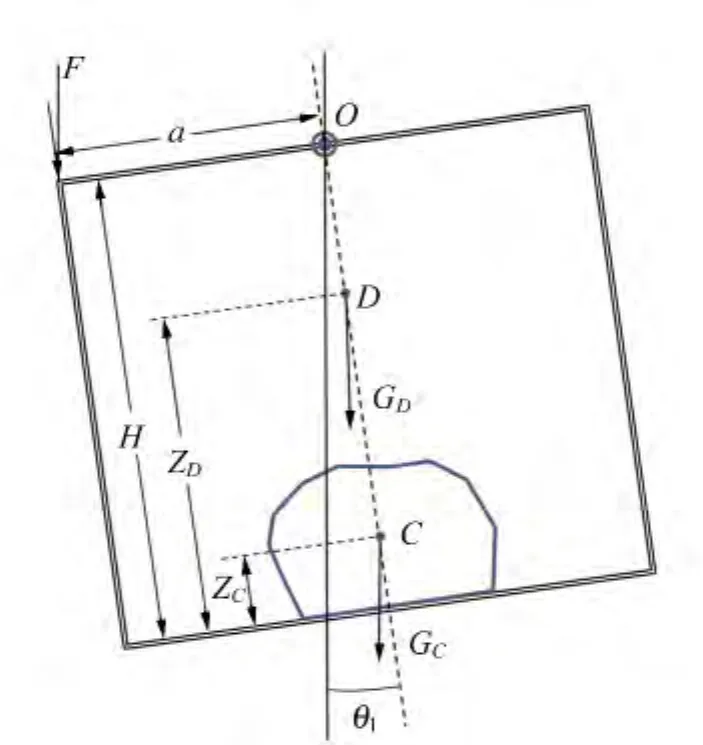
图2 实验装置测量原理图

将刚体放入转动惯量架内.为提高测量精度，转动惯量架底部设有刚体定位装置(4个对称放置的轻质双面吸盘)，确保刚体在转动惯量架内不会晃动.为保证转动惯量架偏转角为零，需要再次调节转动惯量架上的平衡螺母，必要时可以通过调节吸盘的位置来调整刚体重心的具体位置，使得倾角传感器示数为零.给转动惯量架施加外力F2使其发生微小偏转，偏转角为θ2，根据力矩平衡原理可得刚体Z方向重心位置为

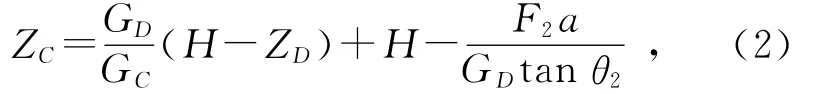
其中，GD为转动惯量架的重力，GC为刚体的重力，H为转动惯量架的高度.

3.3 刚体转动惯量的测量

对于转动惯量架，由复摆的摆动方程

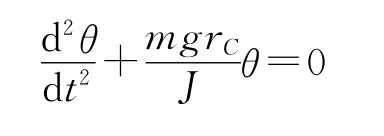
得到摆动周期

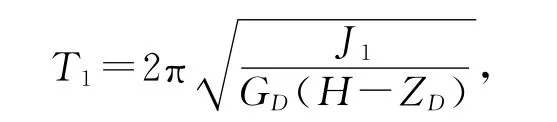
若测得转动惯量架的摆动周期即可得到转动惯量架的转动惯量为

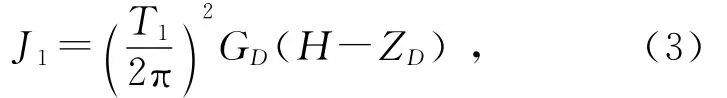
放入刚体后整个摆动系统的转动惯量为J2，摆动周期可表示为

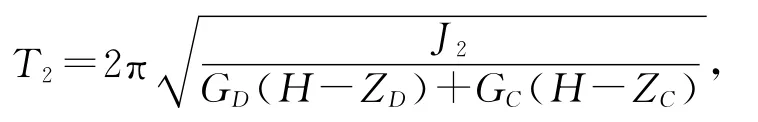
整个摆动系统的转动惯量为

刚体绕通过其重心转轴的转动惯量为JC，根据平行轴定理得：

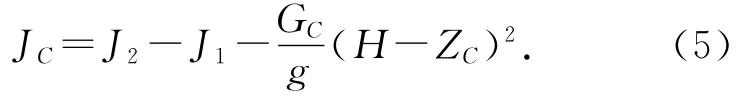
4 实际测量举例

测量转动惯量架的转动惯量数据如表1所示，其中H＝244.76mm，GD＝1733.2g，a＝120.51mm.

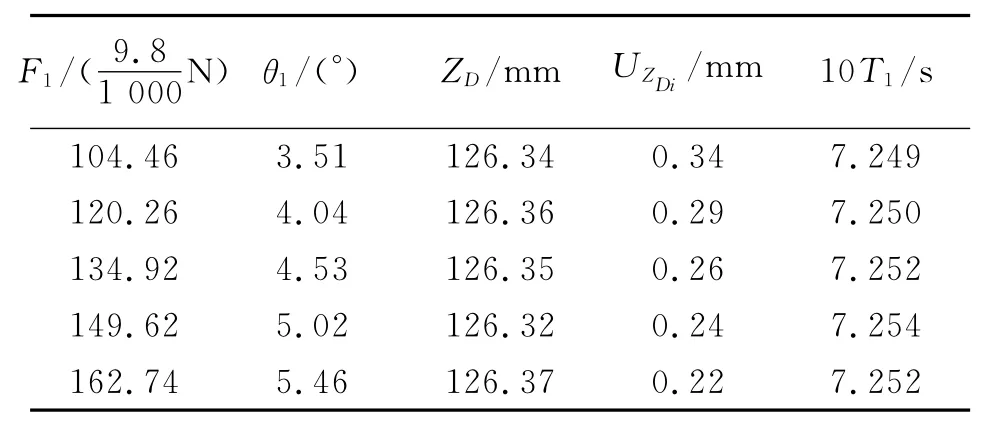
表1 转动惯量架的测量数据

对ZD和T1进行了5次测量，每次的测量条件不同，属于不等精度测量.所以，ZD的最终结果应该用加权平均法来计算.设每次测量值为ZD1，ZD2，ZD3，ZD4和ZD5，其对应的权分别为P1，P2，P3，P4和P5.我们认为如同不确定传递公式符合标准偏差传递公式一样，实验结果用不确定度评定后，加权平均法仍然适用，只需在加权平均公式中将标准偏差换为不确定度即可[8－10].首先需要计算测量值ZDi的不确定度.由式(1)可知ZDi是间接测量量，其不确定度取决于测量值H，F1，a，GD和θ1.于是，根据间接测量量的不确定度公式

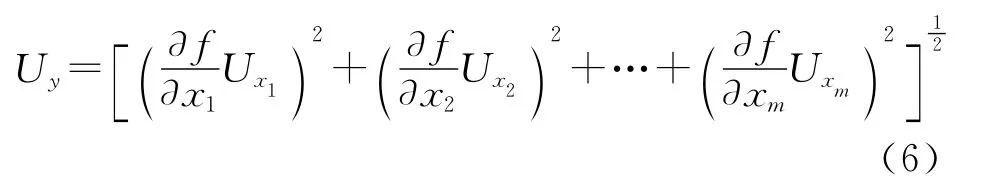
可求得ZDi的不确定度UZDi，取权，则ZD的加权平均值为

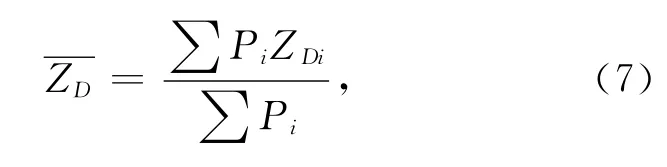
加权不确定度为

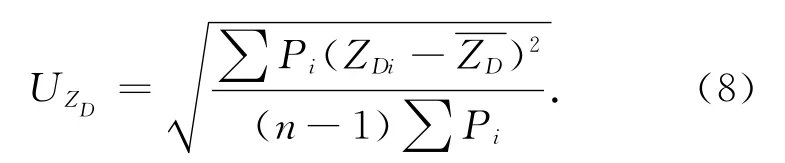
为了验证该装置测量数据的准确性，测量了铝制圆柱体绕其中心轴的转动惯量，圆柱体的质量m＝1.3572kg，半径R＝40.00mm，长L＝100.00mm.测得数据如表2所示.

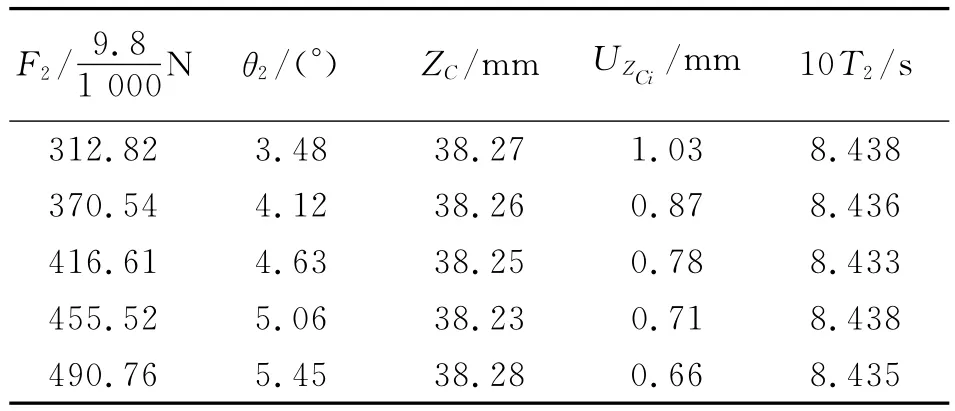
表2 铝制圆柱形刚体的测量数据

同样对于ZC和T2进行5次测量，也属于不等精度测量.根据(7)～(8)公式计算得到，ZC的加权平均值为将代入式(4)得到整个转动系统绕O点的转动惯量将J2，J1和J′代入式(5)可得铝制圆柱体绕其中心轴的转动惯量为JC＝1.105×10－3kg·m2.

根据质量均匀分布的圆柱形刚体绕重心转轴的转动惯量计算公式可得到JC的理论值：

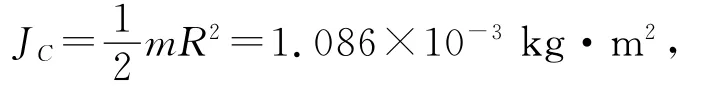
于是，测量结果的相对偏差为

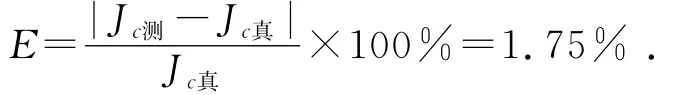
5 结束语

根据复摆测量转动惯量的原理，设计了测量不规则刚体转动惯量的装置，采用了传感器测量技术(比如压力传感器、对射式光电计数器、倾角传感器等)，具有测量方便、速度快、实验原理与理论联系密切、智能化程度高等优点.该装置充分利用了物理天平的底座和游码标尺支架，设计巧妙.

[1]东南大学等七所工科院校.物理学[M].5版.北京：高等教育出版社，1999.

[2]姚启钧.光学教程[M].北京：高等教育出版社，2002.

[3]葛宇宏，葛志利.三线摆摆线质量对转动惯量精确测量的影响[J].力学与实践，2012，34(6)：50－54.

[4]汪仕元，朱俊，穆万军，等.对扭摆式刚体转动惯量测量仪载物装置的改进[J].物理实验，2013，33(5)：40－42.

[5]袁昌盛，宋笔锋.改进复摆法测量转动惯量的方法和设备研究[J].中国机械工程，2006，17(6)：598－600.

[6]王学水，鲁守宝.基于SX1212的刚体转动惯量无线数传系统[J].物理实验，2013，33(2)：33－35.

[7]贾昱，程敏熙，安盟，等.基于视频分析软件Tracter测量刚体转动惯量[J].物理实验，2014，34(5)：13－16.

[8]魏诺，史彭，张伯乾，等.非等精度测量不确定度表示两种方法的比较[J].高校实验室工作研究，1999(2)：35－36.

[9]金哲，崔玉子.有限次不等精度测量的数据处理及测量精密度评定[J].延边大学学报(自然科学版)，2004，30(4)：254－256.

[10]关荣华，于慧.牛顿环实验测量结果的不确定度评定及其表示[J].大学物理实验，2001，14(3)：60－62.