基于CFD 的混凝土轻舟船型阻力性能优化
葛 斌,胡坚城,黄蕴钰,章 颜
(同济大学 土木工程学院,上海200092)
0 引言
混凝土轻舟是ASCE主办的美国赛中提出的一项比赛课题,在限定其长度不得超过6.7 m,宽度不得超过0.9 m的前提下,进行双人、4人200 m或600 m划行等比赛,从速度、密度、转角灵敏度、稳定性等几个方面衡量混凝土轻舟性能。
本文以2014年同济大学混凝土轻舟队在ASCE混凝土轻舟赛中的参赛轻舟为优化对象,欲在现有基础上对轻舟的船型做进一步改进。影响轻舟速度、密度、灵敏度和稳定性等几大性能的主要因素有船型、船重、水流条件等[1],其中船型是重中之重,而阻力最小的船体外形确定又是船型设计首先要追求的目标[2—4]。影响船型阻力的因素可分为横剖面面积、设计水线、横剖面形状、船首船尾形状等,而本文将以船长、型宽和最大横剖面位置作为研究对象。
1 船舶设计理论分析
1.1 主要技术性能的分析
轻舟比赛是一项竞速性比赛,船型对耐波性与稳定性的要求不高,而对快速性提出了极高的要求,因而设计时主要考虑船体的快速性。解决快速性问题主要是选择合适的主尺度,优化船型,降低涡流阻力(形状阻力)[1]。
在船型设计中,影响快速性的因素主要有:长宽比、最大横剖面位置、横剖面形状以及船首船尾的构造。由于本文只限于二维船型设计分析,故以船长、型宽与最大横剖面位置为主要研究对象。
1.2 主尺度的考虑与选择
1.2.1 统计分析与初步选择
首先,作者对其他各参赛学校的从2000年—2013年共75艘船型进行了研究与统计,关注的重点在于船长、型宽与长宽比。统计发现,各学校采用的船型尺寸在一定范围内变化,特别是取得优异成绩的船型主尺度具有一定规律。可得出以下结论:
(1)排名靠前的船长L:6.0~6.8 m;排名靠前的型宽B:0.66~0.81 m。
(2)L/B的取值在8.0~8.8较合适;当L/B>10.0时,普遍成绩较差。
这些数值是基于10多年的参赛学校的成绩统计值,因此具有一定的可靠性,本文所研究的范围尺度也是在此基础上。但由于此范围较宽泛,为获取更精确的值,本文进行了深入的理论分析。
1.2.2 船长的确定
考虑到船身越长,造价越高,且转弯性能越差,而比赛中弯道所耗费的时间约占总耗时的1/3。为了减少转弯带来的不利影响,决定在上述结论上选择最小船长作为研究对象,即选定船长为6 m。
1.2.3 型宽和最大横剖面位置的确定
1.2.3.1 型宽B
(1)傅汝德数Fn
根据以往的比赛成绩,排名靠前的轻舟划行200 m直线距离所需时间t一般为90~120 s。可得傅汝德数的范围为其中,g为重力加速度,g=9.8 m/s2。设计时取t为105 s,则 Fn=0.255。
(2)方形系数Cb
由方形系数的估算公式(亚历山大公式适用于Fn <0.30)[1]可得:Cb=0.63。
(3)长宽比L/B
由方形系数Cb确定长宽比 L/B[1]:L/B≈6.8。则B=0.88 m。
1.2.3.2 最大横剖面位置
根据已有的优良型线面积曲线的一般特性,对经验公式进行修正后可得到适宜的进流段长度公式:
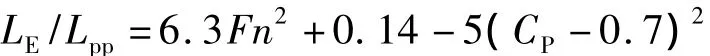
式中:LE为进流段长度,Lpp为船长,CP为棱形系数,Cp=Cb/Cm(Cm为中横剖面系数补充)[1]。
根据文献[1],Cb、Cm与 Cp的关系曲线图可得Cp约为0.63~0.66,故 LE/Lpp=0.525~0.542。
因而进流段长度LE=3.15~3.25 m,也即最大横剖面位置位于中点偏后0.15~0.25 m。
显然L/B=6.8的结论与上文中的长宽比适宜范围相差较远。这是由于经典船舶设计理论中的型线设计考虑因素较综合,没有突出快速性的要求,因此本文寻找的最优宽度与最大横剖面位置可能与上述结论存在出入。本文拟使用CFD方法进行数值模拟,以期得到一个更优的选择。
2 船型优化思路
2.1 基本假定
(1)对于船舶粘性绕流来说,根据运动的相对性原理,轻舟在静水中划行时,可等效为轻舟静止而水流以舟的速度流动。两边的河岸可设为管道壁,转化为流体在管道中的流动问题。
(2)将轻舟的划行看成匀速,即忽略人员划桨的不连续性,故可将水流设为匀速。
(3)由于转弯时分析较为复杂,故本文只考虑轻舟在直线划行时的数值模拟。
(4)忽略轻舟的操纵难易程度,只把轻舟划行时产生的阻力作为唯一评判指标。
(5)忽略由于宽度和最大横剖面位置改变所引起的设计水线的变化。
(6)由于本文只考虑二维船型,即船长、船宽、最大横剖面位置这几个参数。而船长L经上文分析已确定,结合对往年各参赛船型的分析,得到型宽的范围B=0.66~0.81 m。由经验分析得到的最大横剖面位置X=3.15~3.25 m,在建模时将范围放大至X=3.0~3.30 m,对这2个参数进行组合得到以下24个不同模型进行二维建模:
船宽 B:0.66、0.69、0.72、0.75、0.78、0.81 m。最大横剖面位置 X:3.0、3.1、3.2、3.3 m。
2.2 船型设计
本文以2014年同济大学混凝土轻舟队在美国ASCE混凝土轻舟赛中比赛用船作为优化对象。该船的船长6.19 m,型宽0.68 m,最大横剖面位置距离船头约3.4 m。该船的船型如图1所示。

图1 2014年ASCE混凝土轻舟赛同济大学参赛船只
在大部分区段,该船的两侧壁垂直于水面,因此符合本文的基本思想,这为本模型得出较精确的解提供了保障。
通过Freeship等船型设计软件,可以调整船型,并获取船壁上任意点的坐标。通过一定的运算法则,可以将6.19 m的船型等效为6.0 m的船型;通过改变宽度及最大横剖面的位置,可以得到不同的船型,从每个船型的船舷中选取20个控制点用于建模。以X=3.0 m,B=0.66 m时的船型曲线为例,如图2所示。
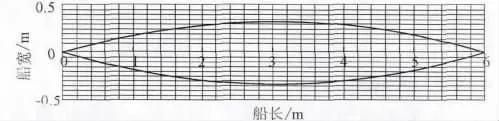
图2 X=3.0 m时的船型曲线
3 网格建立
本文中使用的网格由 GAMBIT软件生成。GAMBIT是fluent的专业前处理软件,生成的网格可直接导入fluent计算,其能够生成结构和非结构2类网格。本文模型采用非结构化网格划分方式,面网格采用Tri-Pave划分方式。边界层共设4层,第1层为0.05。网格的尺寸及划分结果如图3所示。
4 数值方法和理论计算
4.1 控制方程
流体流动符合质量守恒、动量守恒和能量守恒3大基本守恒定律。如果流动处于湍流状态,系统还要遵守附加的湍流控制方程。控制方程是这些守恒定律的数学描述[5]。
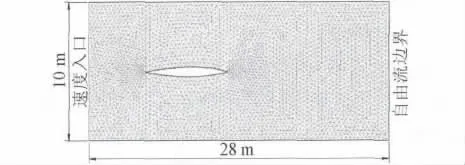
图3 网格划分结果
4.2 湍流模型
本文选用标准k-ε模型,具有数值稳定性好、求解压力梯度精确等优点,是目前船舶粘性流动和粘性水动力求解应用最广泛的湍流模型。
4.3 边界条件
(1)入流边界条件:速度入口(velocity inlet),模拟水流速度为2.3 m/s。
(2)出流边界条件:由于控制域出口处离船尾部较远,经过初步计算后发现出口处来流未受到船体的扰动影响,故可设为自由流边界(outflow)。
(3)船体:设为无滑移壁面(wall)。考虑壁面粗糙度。
4.4 数值方法
4.4.1 方程离散
有限体积法(FVM)考虑在体积元边界流出的矢通量等于相邻体积元在该边界流入的矢通量,从而保证了差分格式的守恒,因而即使在网格比较粗的情况下也能准确地显示出积分守恒。同时FVM能采用各种形状的网格以适应各种形状的边界几何形状。fluent软件采用它来进行离散求解。
4.4.2 求解算法
本文采用SIMPLEC算法进行压力-速度的耦合求解。离散格式均采用二阶精度格式。
5 数据分析
从图4、图5可以得出以下2点结论:
(1)当型宽相同的情况下,以0.72 m为例,随着最大横剖面位置从船中3.0 m的位置往船尾移动,总阻力是先减小后增大,在3.2 m附近的位置减到最小。船宽为0.75、0.72、0.69、0.66 m时都基本符合上述规律,而0.81、0.78 m时结论有偏差。导致偏差的原因可能有:数值计算的系统误差;当型宽较大时(如大于0.78 m),在3.2 m附近总阻力最小的结论不满足。
(2)当最大横剖面位置相同时,随着型宽的增大,总阻力逐渐增大。
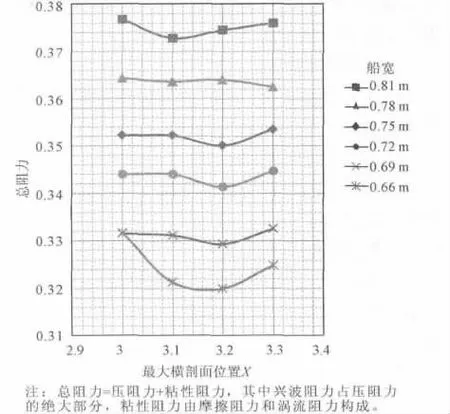
图4 最大横剖面位置与总阻力的关系
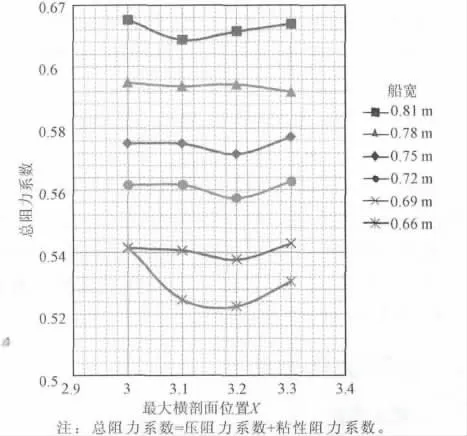
图5 最大横剖面位置与总阻力系数的关系
为了保证网格划分的质量,作者对24个模型的壁面Yplus进行了统计(见图6),发现均在53~55之间,说明模型网格划分质量良好。
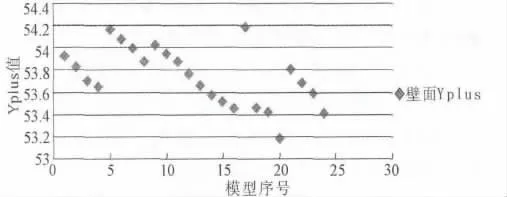
图6 Yplus值
总结可得出以下结论:
(1)当型宽小于0.78 m时,最大横剖面位置X=3.2 m时船体所受总阻力最小。
(2)型宽越大,总阻力越大,当B=0.66 m时,总阻力最小。
6 结论
本文通过统计分析、经典船舶设计理论分析与fluent软件模拟等多方面分析,通过对复杂外形船体的二维模型建立,在船舶设计过程中优化船舶阻力的性能。从计算结果分析,得到如下2点结论:
(1)通过fluent数值模拟结果可知,优化后的船型最大横剖面位置约为3.20 m处,此时总阻力最小,与经典船舶设计理论计算所得的3.15~3.25 m处吻合。
(2)在一定范围内,长宽比L/B与快速性成正相关[1]。而在1.2.1的统计结果中对L/B有一定限制范围,这是由于当L/B过大时,会对船体的稳定性造成较大影响。可取L/B=8.8,则优化后的船宽宜选0.68 m。
[1] 顾敏童.船舶设计原理[M].上海:上海交通大学出版社,2001.
[2] 马坤,田中一朗.最小阻力船型优化研究[J].水动力学研究与进展,1997,12(1):113-122.
[3] 陈京普,朱德祥,何术龙.双体船/三体船兴波阻力数值预报方法研究[J].船舶力学,2006,10(2):23-29.
[4] 郦云,卢晓平.高速三体船阻力性能研究[J].船舶力学,2007,11(4):191-198.
[5] 周美,邢殿录.流体力学[M].大连:大连理工大学出版社,2003.

