基于型值表的船舶容积近似计算方法

谭宝殊，王 义

(北京数码易知科技发展有限责任公司，北京100007)

0 引言

船舶线型具有多变特点。通过研究发现，船舶线型多变主要体现在尾部，一般包括单隧道船型、双隧道船型、双艉鳍船型和双体船型等4类。常规船型的横剖面的水线和船壳曲线一般仅2个交点，而这几类特殊船型横剖面中，水线和船壳曲线超过2个交点。遵照还原常规船型思路，寻求一种简单有效的方法，即通过型值拆分，将特殊船舶线型转化为常规船舶线型求解船舶量吨甲板以下容积。

1 常规船型

1.1 主型值表设计

基于船舶三维立体反映的设定见表1主型值表［1］。设定船舶艉垂线、基线、中纵剖线交点坐标原点。表1中，X为船长方向横剖面距艉垂线的距离，m;Y为型宽方向半宽值，m;Z为型深方向高度值，m。

表1 主型值表

主型值表结合船体近似计算方法求解船舶量吨甲板以下容积。

1.2 计算方法

由于计算方法非本文研究重点，仅研究梯形法［1］和辛普生［1］第一法 2 种计算方法。

1.2.1 梯形法

梯形法近似计算的基本原理是用若干直线段组成的折线近似地代替曲线，即以若干梯形面积之和来代替被积函数曲线下所包围的面积。

如图1所示，将一个曲线图形的底边分成间距为 l1、l2、…、ln-1、ln的 n 份，其纵坐标值分别为 y0、y1、y2、…、yn-1、yn;B、C 为曲线的起点和终点。

则在第0号和第1号纵坐标内的面积A1为:

在第1号和第2号纵坐标内的面积A2为:

依次类推，最后得到在第n-1号和第n号纵坐标内的面积An为:

整个曲线围成的面积和A为:

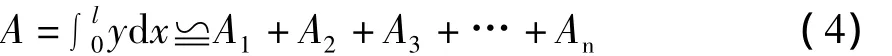
图1 梯形法图形

1.2.2 辛普生第一法

辛浦生第一法也称抛物线法，又简称辛浦生［1，4，1］法，是采用等分间距，以若干段二次抛物线近似地代替实际曲线，计算各段抛物线下面积的数值积分法。

如图2所示，将一个曲线图形的底边分成等间距为l的n等分(n必须为偶数)，其纵坐标值分别为 y0、y1、y2、…、yn-1、yn。

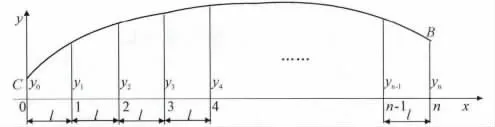
图2 辛普生第一法图形

则在第0号和第2号纵坐标内的面积A1为:

在第2号和第4号纵坐标内的面积A2为:

依次类推，最后得到在第n-2号和第n号纵坐标内的面积Ai为:

整个曲线围成的面积和A为:

2 特殊船型

2.1 线型分析

针对单隧道船、双隧道船、双艉鳍船、双体船4种特殊线型［3］横剖面特征简单示意进行分析，水线面同理。

2.1.1 单隧道船线型分析

如图3所示，单隧道船型横剖面的面积=区域Ⅰ的面积-区域Ⅱ的面积。图3中，P1表示隧道底点，P2表示隧道顶点。

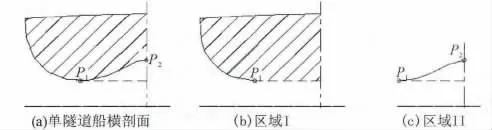
图3 单隧道横剖面

2.1.2 双隧道船线型分析

如图4所示，双隧道船型横剖线面的面积=区域Ⅰ的面积-区域Ⅱ的面积+区域Ⅲ的面积。图4中，P1表示隧道外侧底点，P2表示隧道顶点，P3表示隧道内侧底点。

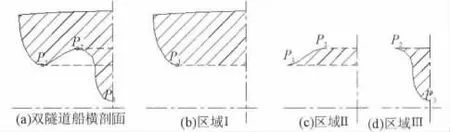
图4 双隧道横剖面

2.1.3 双艉鳍船线型分析

如图5所示，双艉鳍船型横剖面的面积=区域Ⅰ的面积-区域Ⅱ的面积+区域Ⅲ的面积。图5中，P1表示艉鳍外侧底点，P2表示艉鳍顶点，P3表示艉鳍内侧底点。

图5 双艉鳍横剖面

2.1.4 双体船线型分析

双体船型横剖面面积计算同单隧道船型。

2.2 附加型值表设计

通过特殊线型分析发现，单隧道船与双体船特征相似，双隧道船与双艉鳍船特征相似。

本文表1常规船型主型值表仅满足区域Ⅰ的需要，于是追加设计表2附加型值表满足区域Ⅱ和区域Ⅲ的计算需要。

2.3 计算方法

考虑梯形法和辛浦生法优缺点，综合运用这2种方法进行计算。通过主型值表和附加型值表，结合前面特殊线型的分析，采取分别计算主型值表和附加型值表，计算值扣除方式，即:船舶量吨甲板以下容积=主型值表计算值-附加型值表计算值。

主型值表将船舶拆分成首部、主体部分和尾部3段进行计算。主体部分指船舶首垂线和尾垂线之间的部分，该部分一般为0站至20站(或者0站至10站)。采用辛浦生［1，4，1］法，提取型值表数据，采用横剖面近似二次抛物线，依次计算各站横剖面面积，沿船长积分计算主体部分体积。首部指船舶首垂线和首端之间的部分，即末站到首端。考虑不同船型的首部型线多变化，提取型值表末站到首端的数据，采用水线面近似二次抛物线，深度方向近似梯形方法进行计算。尾部指船舶尾垂线和首端之间的部分，即0站到尾端。提取型值表0站到艉封板的数据，采用辛浦生［1，4，1］法近似二次抛物线进行计算。另外，根据特殊船舶的特征，增加突出体计算项。最后将船舶主体部分、首部、尾部、突出体相加即求为量吨甲板以下容积。

附加型值表通过提取型线图中隧道处顶线、底线数据，采取梯形法数据加密近似计算。

表2 附加型值表(内)和(外)

3 计算实例

3.1 常规船型

针对常规船型，采用辛浦生法进行计算，验证主型值表设计有效性。计算结果对比见表3。

3.2 特殊船型

以下针对单隧道船和双隧道船2个船型计算，本文只为验证拆分型值表合理性，简单采用梯形法进行计算，单隧道船、双隧道船计算结果对比分别见表4、表 5。

4 结语

通过对船舶线型分析，总结一般规律，采用常规主型值表和附加型隧道型值表，计算船舶量吨甲板以下容积，满足近似计算要求，证明复杂船型拆分型值表合理性。该方法后经程序开发，作为“船舶吨位丈量计算模块”之型值表法集成在海事局“船舶吨位丈量管理系统”中使用，全面通过海事局实际运用验证。后续可根据需要，采用辛普生法、乞贝雪夫法等方法进一步提高计算精度，亦可以考虑引入船舶三维几何精确计算。在此基础上通过公式和插值方法，求得任一吃水下型排水体积及其他静水力参数，可以进行船舶静水力计算。

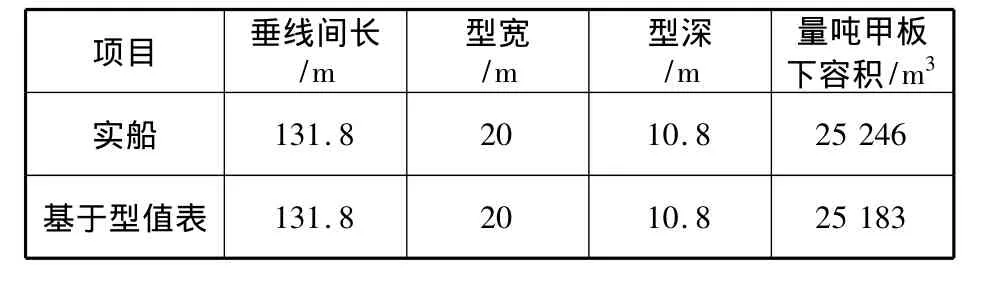
表3 常规船型计算结果对比

表4 单隧道船型计算结果对比

表5 双隧道船型计算结果对比

［1］ 盛振邦.船舶静力学［M］.上海:上海交通大学出版社，1992.

［2］ 船舶工业总公司.船舶设计实用手册［M］.北京:国防工业出版社，1998.

［3］ 朱珉虎.船舶设计手册［M］.北京:中国标准出版社，1996.