基于弹性支承的磁悬浮轴承转子系统振动控制

华 燕，张发品，周 瑾

（1.上海航空工业（集团）有限公司，上海200232；2.上海飞机制造有限公司，上海200436；3.南京航空航天大学机电学院，江苏 南京210016）

0 引言

磁悬浮轴承与传统轴承相比，其轴承与转子之间无机械接触，从而可以得到更高的转速，同时具有更小功耗等传统轴承无可比拟的优点，在透平机、压缩机等领域正逐渐得到越来越广泛的应用［1－2］。然而磁悬浮轴承在抑制振动方面因自身的刚度阻尼调节范围较窄，有着先天不足，尤其在系统过临界时，容易因转子振幅过大而发生碰磨，甚至引发事故［3－4］。因此，寻找一种有效的减振手段就显得尤为重要。

为寻找有效的振动抑制方法，有必要对系统动力学特性进行充分分析，这涉及到固体力学分支——转子动力学。求解转子动力学问题通常采用传递矩阵法和有限元法。因前者将转子系统简化成一系列极简单的集中质量点－梁模型，使模型完整性和求解精度难以保证。后者相较于前者，所建立的模型完整性得到很大提高，更接近转子真实结构，适应性更强，在转子临界转速计算和不平衡响应分析等问题解决上有着突出优点，使求解更为简单可行。因此，下面基于有限元软件ANSYS，采用有限元法建立转子系统有限元模型，以对其动态特性进行仿真分析。

1 建立转子动力学模型

试验台磁悬浮转子系统所用转子如图1所示，在光滑阶梯轴中间设置有驱动电机硅钢片组，两端分别设置有径向和轴向磁悬浮轴承硅钢片组。在ANSYS 14.0中的梁单元BEAM188是两节点三维线性有限应力梁单元。该梁单元基于铁木辛柯（Timoshenko）梁理论，可将梁发生变形后剪切变形对系统动态特性的影响考虑在内，十分适用于细长到中等粗短梁的分析。因此，选用该BEAM188单元来模拟本文中的转子。另外，将该转子简化为若干集中质量，并选用单节点的MASS21单元模拟。对于转子系统的两端径向和轴向磁悬浮轴承则选用COMBI214单元模拟。确定单元后利用ANSYS建立的转子有限元模型如图2所示。图中M0表示集中质量点，K0表示弹簧阻尼单元。所建有限元模型共包括111个节点，110个梁单元，左右两处径向磁悬浮轴承分别对应于节点18和节点97。

图1 转子实物

图2 转子有限元模型

为保证后续仿真分析的准确性，通过有限元法计算上面建立的转子有限元模型在自由－自由状态下的临界转速，并与转子在自由－自由状态的模态试验结果进行对比验证。

1.1 有限元法计算自由－自由状态临界转速

在ANSYS中基于上面建立的转子有限元模型，并将磁悬浮轴承的刚度和阻尼均取为零以模拟转子的自由－自由支承状态进行模态求解，得到转子的前三阶弯曲临界转速，如表1所示。

表1 ANSYS有限元分析得临界转速

1.2 模态试验得自由－自由状态临界转速

采用泡沫垫支承转子来模拟转子自由－自由状态进行模态振动测试试验。利用锤击激励法对转子上选定的10个测试点进行敲击，并在非振动节点处布置传感器采集振动数据。分析测试所得数据，得到前三阶模态振型，如图3～图5所示

将有限元法计算的转子自由－自由状态下临界转速与模态试验所得结果对比，如表2所示。

表2 ANSYS仿真与模态试验值对比

由表2可知，利用ANSYS计算得到的临界转速值与模态试验值十分接近，所存在的误差在可接受范围内，说明利用ANSYS建立的有限元模型准确可靠，可用于对系统动态特性的仿真分析。

图3 转子一阶弯曲模态振型

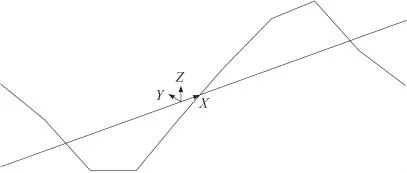
图4 转子二阶弯曲模态振型

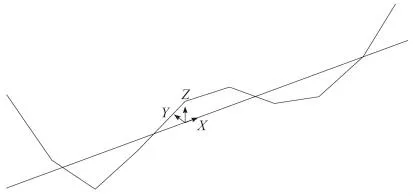
图5 转子三阶弯曲模态振型

2 系统动态特性仿真分析

磁悬浮转子系统原理如图6所示。为简化处理，假定两端径向磁悬浮轴承刚度相同且阻尼相同，以K1和C1表示，轴向磁悬浮轴承刚度和阻尼则以K3和C3表示。两径向轴承支承处分别对应于节点18和节点97。

图6 磁悬浮轴承支承转子系统原理

基于ANSYS转子动力学模块，取磁悬浮轴承支承刚度为K1＝5.0×106N／m，在转子上节点13和68两处均添加大小为7.5×10－6kg·m的不平衡量，阻尼C1分别取为50N·s／m、500N·s／m和1 000N·s／m。为确保不发生转子碰磨，重点分析两端径向磁悬浮轴承对应节点，即节点18和97。下面对节点18处的转子稳态不平衡响应进行仿真。图7为节点18的稳态不平衡响应。

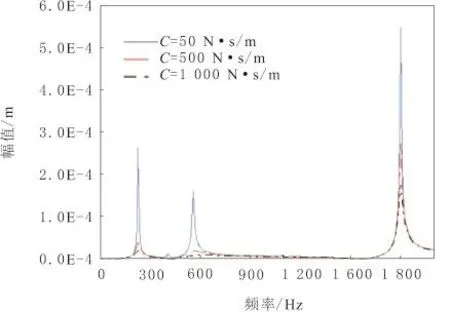
图7 不同磁悬浮轴承阻尼下的稳态响应

从图7可知，转子振动幅值随着磁悬浮轴承阻尼的增加而减小，即磁悬浮轴承阻尼可以有效抑制转子振动，因此为了控制磁悬浮轴承柔性转子系统的振动，可以考虑增大阻尼。磁悬浮轴承刚度和阻尼的大小依赖于控制系统中参数的设定，而参数设定的主要目标是使转子能够稳定悬浮。为了降低磁悬浮轴承为减小转子振动所付出的代价，可以在原有磁悬浮轴承结构以及一般控制方法的基础上，附加额外的刚度阻尼支承，如电流变液阻尼器、磁流变液阻尼器以及挤压油膜阻尼器等。另外，现有文献也指出，合理的外弹性支承可有效抑制系统振幅，并同时提高系统稳定性，即要减小系统振幅可以通过外加合适的刚度阻尼结构来实现。下面对外弹性支承引入前后转子系统不平衡响应进行对比。

将磁悬浮转子系统置于外弹性支承上，并假定附加的两端支承处刚度和阻尼分别相等，且分别为K2和C2，则系统原理图如图8所示。

在节点13和节点68处均添加大小为7.5×10－6kg·m的不平衡量，取磁悬浮轴承的支承刚度K1＝5.0×106N／m，阻尼C1＝50N·s／m，外弹性支承的刚度K2＝1.0×106N／m，阻尼C2分别取值为50、500和1 000N·s／m，得出在0～1 000Hz内磁悬浮轴承支承节点18处的不平衡响应，并进行对比，得到图9。

由图7和图9可知，外弹性支承的引入可以明显降低磁悬浮转子系统的振幅，且外弹性支承的阻尼越大，抑制能力越强。

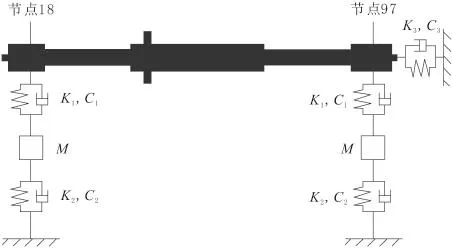
图8 系统原理

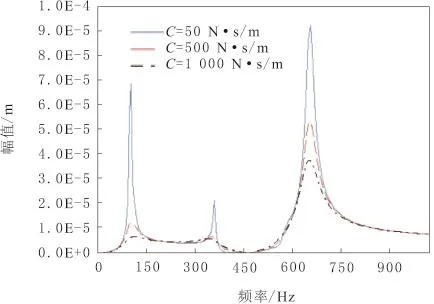
图9 不同外支承阻尼下转子系统不平衡响应对比

3 试验验证

3.1 试验方法

为验证弹性支承的引入可有效抑制磁悬浮转子系统的振动，搭建磁悬浮轴承转子系统试验台。磁悬浮系统控制箱通过PID控制算法调节控制电流大小，实现磁悬浮轴承运转时的稳定悬浮。变频驱动器则调节电机转速，实现转子匀加匀减速运转。在转子径向安装电涡流传感器测量其振动位移，并由数据采集卡采集输入至终端LabVIEW监测系统中进行记录和在线显示。

另外，由于金属橡胶作为一种新型的低密度多孔阻尼材料，具有良好的大阻尼性能［5］，因此将其加工成环状，如图10所示，并外置于两径向磁悬浮轴承上作为阻尼器来为系统提供合适的弹性支承。

图10 金属橡胶环实物

转子系统振动的最大幅值通常由其加减速跨越临界转速时的时间长短决定。因此，转子系统通过临界转速时的过程由瞬态响应特性进行分析更加合适。

另外，囿于现有条件限制，难以准确获取试验中所用金属橡胶环刚度和阻尼具体大小。因此，本试验仅从其可提供良好的刚度阻尼角度进行定性分析，并通过与引入前响应对比，验证外弹性支承的振动抑制效果。

试验时，首先将磁悬浮轴承转子静态稳定悬浮后，通过中间的变频驱动电机使转子在90s内由0 Hz匀加速运转至550Hz，采集该起动升速过程中转子位移信号，并以同样方法得到有阻尼器时的情况。

3.2 试验结果

利用数据分析软件Matlab对3.1中采集到的试验数据进行处理，得到有无金属橡胶阻尼器作为弹性支承时系统左侧支承处瞬态不平衡响应对比曲线，如图11所示，其中实线表示无阻尼器时的响应，虚线表示有阻尼器时的响应。

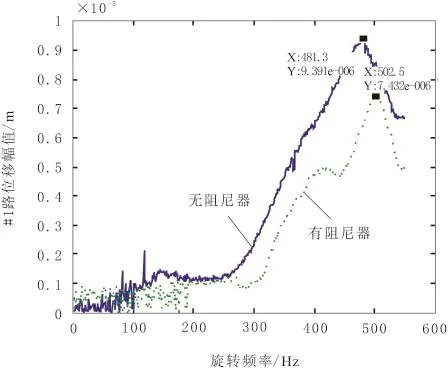
图11 起动时左侧支承处有无阻尼器对比

由图11可知，由于外弹性支承的引入，虽然没有改善系统在0～250Hz低频范围内的振动，但是，相较对于引入之前，系统一弯振幅降低约为21%，在250～550Hz范围内的转子振动得到了有效地抑制。

4 结束语

通过仿真及试验研究，表明在磁悬浮转子系统中引入合适的外弹性支承，对系统振动抑制是有效可行的。同时，相较于目前常用的挤压油膜阻尼器，将金属橡胶作为阻尼元件来进行转子振动控制，既无需润滑，也可以有效避免"双稳态"、"锁死"等不利现象发生。然而，试验囿于条件限制，仅对外弹性支承对系统振动抑制效果进行了定性分析。如能准确获得金属橡胶材料的刚度阻尼值，则可参照前述仿真，取3组不同刚度阻尼的金属橡胶环进行进一步的试验研究。

［1］ Akira Chiba，Tadashi Fukao，Osamu Ichikawa，et al.Magnetic Bearings and Bearingless Drives［M］.Butterworth-Heinemann，2005.

［2］ 汪希平，章东义，张钢，等.电磁轴承及其系统设计方法［J］.机械工程学报，2002，38（5）：1-6.

［3］ YU Suyuan，YANG Guojun，SHI Lei.Application and research of the active magnetic bearing in the nuclear power plant of high temperature reactor［C］／／Proc.of the 10th Int.Symp.on Magnetic Bearings.Martigny：ETH，2006.

［4］ Kai A，Christoph S，Rainer N.Active balancing of a supercritical rotor on active magnetic bearings［C］／／Proc.of the 10th Int.Symp.on Magnetic Bearings.Martigny：ETH，2006.

［5］ ЧегодаевДЕ，МулюкинОП，КолтыинБВ，等.金属橡胶构件的设计［M］.李中郢 译.北京：国防工业出版社，2000.