汽车侧倾角速度传感器的故障诊断和重构

王德军,宋石尧,王晰聪

(吉林大学 通信工程学院,长春 130012)



汽车侧倾角速度传感器的故障诊断和重构

王德军,宋石尧,王晰聪

(吉林大学 通信工程学院,长春 130012)

针对汽车侧倾角速度传感器故障对控制系统的影响问题,提出了一种基于模型的故障诊断和故障重构方法,并给出了系统的理论证明。对于满足Lipchitz条件的多输入多输出非线性系统,可应用带有模型不确定性的一维线性状态方程作为其等效模型,进行传感器的故障诊断。并在此基础上应用经典的观测器理论设计了残差生成器,通过特征结构配置的方法,证明了模型不确定性、执行器故障和干扰可以实现在残差中的完全去耦。采用整车的八自由度模型进行Simulink仿真,结果证明了结论的有效性。与其他方法相比,笔者算法得到的残差具有很强的鲁棒性,重构出的传感器信号具有很高的精度。

故障诊断；故障重构；基于模型；李普希茨；传感器；特征结构配置

0 引 言

近年来,越来越多的人开始关注汽车在主动安全控制和被动安全控制领域的稳定性问题。许多公司和研究机构已经开展了这方面的研究,发表了大量的研究成果,一些成熟的产品已经推向了市场。福特汽车公司的侧倾稳定控制系统是目前成熟的产品之一[1,2],它利用传感器装置监控汽车动态,当汽车有侧翻趋势时,利用控制器对制动力进行分配,以减小侧向轮胎力。在RSC(Roll Stability Control)中,侧倾角速度传感器被用来测量汽车的侧倾动态,一旦发生故障会引起严重的后果。所以,侧倾传感器的故障能否被快速诊断,并且实现相应的故障容错,是RSC实际应用中的关键问题。

通常情况下,侧倾角速度传感器的故障诊断问题可等效为一个非线性系统传感器故障诊断问题[3-5]。目前的诊断方法可大致分为两类： 一类是基于理论的方法[6,7],应用一些成熟的线性系统的故障诊断理论,可解决一部分多输入多输出的非线性系统传感器故障诊断问题,这类方法的有效性已经通过实验的验证,但缺少严格的理论证明,而且残差的鲁棒性不强; 另一类是基于估计的方法[8,9],这类方法通过测量值和系统动态估计值的比较产生残差,有利于判断故障的发生,但由于没有对故障本身建模而导致其不能呈现出故障的细节,对故障的处理工作难以实现,如故障识别和故障容错等,而且由于该方法的实现依赖于实验所获得的大量数据,导致工作量非常大[10-12]。

为此,笔者提出了一种基于模型的方法进行侧倾角速度传感器的故障诊断和故障重构。首先,提出了一种整车的八自由度非线性模型,用于在实验中模拟真实车辆的动态性能；其次,证明了对于满足李普希茨条件的多输入多输出非线性系统,可应用一个带有模型不确定性的一维线性状态方程作为等效模型,代替该非线性系统故障诊断；再次,笔者应用经典的观测器理论设计了残差生成器,并且通过引入辅助状态和特征结构配置的方法,将模型不确定性、执行器故障和干扰在残差中实现了完全去耦；并通过simulink仿真实现了侧倾角速度传感器的故障诊断和故障重构。

1 汽车模型和轮胎模型

1.1 汽车模型

笔者提出了一种整车的八自由度非线性模型(见图1),用于研究汽车侧向稳定控制系统的动力学特性,包括横摆、侧倾、横向、纵向4个自由度和4个车轮的转动自由度[13]。

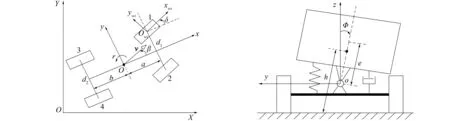
a 底盘部分 b 簧载部分

下面是汽车的运动方程和动力学方程。

横摆运动状态

侧倾运动状态

横向运动状态

纵向运动状态

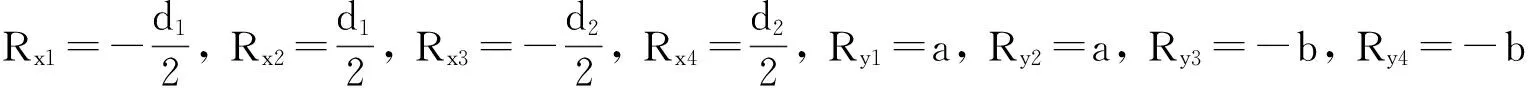
此外,4个车轮的垂直载荷描述如下

车轮运动学方程为

可整理为

其中Tti为第i个车轮上的驱动力矩,Tbi为第i个车轮上的制动力矩,Ji为第i个车轮上的转动惯量,Rli为第i个车轮上的负载半径。

1.2 轮胎模型

笔者采用郭孔辉教授提出的统一指数轮胎模型[14-16],该模型的物理意义清晰,仿真精度高,能更加精确地模拟车轮动态。统一指数轮胎模型是在极限工况下对轮胎力学进行实时仿真的理想模型和用于预测轮胎稳态特性时的半经验模型,可实现轮胎纵滑、侧滑、侧倾等非稳态和非线性工况的仿真实验。

假设胎体只发生横向弹性形变,纵向轮胎力Fx,横向轮胎力Fy,回正力矩Mz分别描述为

2 等价模型

2.1 非线性系统模型的建立

基于模型的故障诊断要求系统具有精确的数学模型,但精确模型很难获得。系统模型是通过物理或数学理论建立的。由于实际工程中,模型通常具有复杂的非线性,而传统故障诊断理论从被控对象的内部结构入手,所以很难得到具有较强鲁棒性的残差,甚至不能设计出残差生成器。

笔者考虑一类满足李普希茨条件的非线性系统,并提出了一个新的建模方法进行传感器的故障诊断： 即以传感器测量的动态为状态,以传感器的测量值为输出值建立状态方程。系统模型为

其中x(t)∈Rn表示状态向量,u(t)∈Rm表示输入,y(t)∈Rn表示输出故障。F和G是合适维度的非线性矩阵。式(11)可以转换成

其中xi(t)表示第i个状态,ul(t)表示第l个输入,yi(t)表示第i个输出,i,j,h∈[0,n],l∈[0,m],fij和ghl是状态和时间的函数,即fij:fij(x1,x2,…,xn,t)和ghl:ghl(x1,x2,…,xn,t)。

进而,式(11)可描述成带有非线性模型不确定性的线性系统

其中aij和bhl是常数,i,j,h∈[0,n],l∈[0,m]。Δaij: Δaij(x1,x2,…,xn,t),Δbhl: Δbhl(x1,x2,…,xn,t)。即Δaij: Δaij(t),Δbhl: Δbhl(t)。但Δaij和Δbhl并非为显函数的形式,且满足Δaij=fij-aij,Δbhl=ghl-bhl。

2.2 目标状态的描述方程

定理1 在式(13)中任意选择一个状态(目标状态),可以被恒等变换成带有模型不确定性的一维状态方程的形式

其输入可为式(13)中的任意一个,模型不确定性是有界的,且是时间的函数。其中a,b和v是常数。a≠0,v∈[1,m],ul(t)表示u(t)中任意1个输入,Mi为模型不确定性。

证明 对于式(13)中任意状态xi,其数学描述为

其中bi∈Rm,Δbi∈Rm,bv∈Rv,Δbv∈Rv,b(m-v)∈Rm-v,Δb(m-v)∈Rm-v为列向量,uv∈Rv,u(m-v)∈Rm-v为行向量,bi=[bi1bi2…bim],Δbi=[Δbi1Δbi2…Δbim]。uv和u(m-v)分别由u(t)中任意v个输入和余下的输入组成。bv和Δbv分别由bi和Δbi中对应于uv的元素组成,b(m-v)和Δb(m-v)分别由bi和Δbi中对应于u(m-v)的元素组成。

令Mi1=Δaiixi+Δbvuv

Mi=Mi1+Mi2

其中模型不确定性Mi由线性关系未能描述的部分Mi1和未建模的部分Mi2组成。由于Lipchitz条件的限制,存在Lipchitz函数γ,满足

‖Φ(x1,u)-Φ(x2,u)‖≤γ‖x1-x2‖

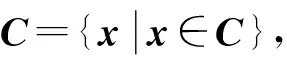
当v=1(只选择一个输入)时

2.3 等价模型的建立

通过定理1,非线性系统(11)中状态xi的测量传感器的故障诊断,可看作一维线性系统(14)的状态xi的测量传感器的故障诊断。因此,可得到非线性系统(11)的等价模型,即式(11)的恒等变换,是精确模型。

在式(14)中加入故障,可得

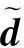
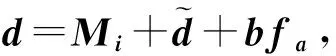
其中d为等效干扰,由对故障诊断产生不利影响因素组成。在状态xi的测量传感器故障诊断问题中,式(19)为系统(11)的等效模型,可代替式(11)解决故障诊断问题。因此,对于非线性系统的传感器故障诊断问题,等价模型(19)的应用可避免对式(11)的内部结构特征的研究,大大减少了工作量。

上述论述提出了一个新的观点,建立等价模型代替被控对象参与故障诊断。等价模型是带有有界模型不确定性的低维线性模型。尽管不能确定模型不确定性是否可用显函数表达,但可以肯定,等价模型在故障诊断问题中是精确模型。

3 问题解法

3.1 基于观测器的方法

基于模型的故障诊断问题的基本工作是设计一个残差生成器,即系统的冗余部分。残差的生成,可理解为系统测量值和相应冗余部分的比较。残差生成器可视为是系统被测量部分的重建,主要方法有故障检测滤波器(FDF),诊断观测器(DO)和等价空间[2]。笔者采用经典的观测器方法检测传感器故障,并且应用经典的特征结构配置的方法实现等效干扰的完全去耦。

通常,含有传感器故障和等效干扰的线性系统可描述为

其中A,B和C为已知的系统矩阵,E为已知的等效干扰的描述矩阵。建立式(20)的线性观测器为

其中K为观测器增益,满足Ac=A-KC稳定。因此,残差为

其中W为加权矩阵,Grd(s)=WC(sI-Ac)-1E,Grfs=-WC(sI-Ac)-1K+W。干扰完全去耦的条件是Grd(s)=0。此时,鲁棒性故障诊断问题变成了寻找适当的W和K,以满足Grd(s)=0且Ac是稳定的。

引理1[17]给定线性系统

其中f表示干扰,Ed,Ef,Fd和Ff为已知的描述矩阵。故障在参差中被完全去耦的充分必要条件是

引理2 如果WCE=0并且矩阵WC的所有行都是相应于Ac的p个特征值的左特征向量,则Grd(s)=0。p是残差的维度[17]。

3.2 故障诊断和重构算法

证明 根据引理2,证明完全去耦可以实现。

经过反拉普拉斯变换,有

所以

通过式(28)中残差的稳态值可知,目标传感器的故障可直观体现。通过残差值和传感器典型故障的数学特征、故障大小和类型可轻易判断。

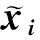
4 仿真验证

4.1 侧倾角速度传感器等效模型建立

笔者提出了一种基于模型的故障诊断和重构的方法,对满足Lipchitz条件的系统具有广泛的适用性。笔者方法中搭建的8自由度整车模型,也适用于该方法,由于针对侧倾角速度传感器故障的等价模型中,模型不确定性也满足Lipchitz条件。具体说明如下。

第2章中的汽车模型方程为

其中参数

输入为

系统的输入具有鲜明的物理意义,即u1,u2,u3分别为车辆所受的纵向力之和∑Fx,侧向力之和∑Fy,横摆力矩之和∑Mz。

根据定理1,建立式(30)的等效模型

为了操作方便,将前轮转角δf作为新的输入引入式(31),此时等效模型与整车具有相同的输入,所以

其中Mi=Δ10ψ+Δ3u2+Δ5u3-δf。显然ψ,u2,u3和δf均连续有界,所以Mi满足Lipchitz条件。

4.2 仿真结果及分析

设定汽车的初始速度为110 km/h,前车轮转角为100 rad,取g=9.8 m/s2,整车其他参数如下M=1 359.8 kg,Ms=1 279.80 kg,R0=0.294 m,lf=1.062 8 m,lr=1.485 2 m,Kfψ=23 540.0,d1=1.414 m,d2=1.422 m,h=0.512 m,e=0.39 m,Iz=1 992.54,Ixs=276.871,Rx1=-Rx2=-0.707 m,Rx3=-Rx4=-0.711 m,J1=J2=J3=J4=1,Cfψ=Crψ=2 810.0,Ry1=Ry2=1.062 8 m,Ry3=Ry4=-1.485 2 m,Rl1=Rl2=Rl3=Rl4=0.29 m,Ixzs=Ixz=0,Krψ=23 101.0。

通过以上的讨论,侧倾角速度传感器故障可以被诊断和隔离。笔者采用基于GPS的方法对车辆的侧倾角进行估计[1]。根据式(21)建立8自由度整车模型的观测器,根据定理5选择W和K,选取a=Δ11,b=1,λ1=λ2=1。图2为系统干扰,图3为侧倾角速度传感器故障,图4为生成的残差,图5为故障重构和故障的比较。

图2 系统的干扰Fig.2 The disturbance in system

图3 侧倾角速度传感器故障Fig.3 The roll rate sensor fault

图4 故障的残差Fig.4 The residual of the fault

图5 故障与其还原值Fig.5 The fault and the fault restored

从仿真结果可以看出,虽然干扰一直存在,但由于完全去耦的作用使其没有对残差产生任何影响；传感器的故障对残差产生影响,并且很快达到稳定；发生故障后很快被重构,并且精度很高。

5 结 语

笔者提出了一种针对满足李普希茨条件的非线性系统传感器故障诊断和故障重构的方法,并且成功应用于车辆侧倾角速度传感器故障的诊断和重构中。该方法操作简单,在工程实践中有积极的意义,也将会对执行器的故障诊断和容错控制起到重要的影响。

[1]LI Xu,H ERIC TSENG.Robust Model-Based Fault Detection for a Roll Stability Control System [J].IEEE Trans Control Systems Technology,2007,15(3): 519-528.

[2]徐颖,刘磊,赵旗,等.ABS实时四轮轮速信号采集系统 [J].吉林大学学报: 信息科学版,2009,47(5): 977-980.XU Ying,LIU Lei,ZHAO Qi,et al.ABS Real-Time Four Wheels Speed Signal Collection System [J].Journal of Jilin University: Information Science Edition,2009,47(5): 977-980.

[3]INSEOK H WANG,SUNGWAN KIM,YOUDAN KIM,et al.A Survey of Fault Detection,Isolation,and Reconfiguration Methods [J].IEEE Trans Control Systems Technology,2010,18(3): 636-653.

[4]ZHANG D,WANG H,LU B,et al.LMI-Based Fault Detection Fuzzy Observer Design with Multiple Performance Constraints fora Class of Non-Linear Systems: Comparative Study [J].International Journal of Innovative Computing,Information and Control,2012,8(1): 633-645.

[5]李爱晨,李香善,焦建宇,等.具有执行器故障的非线性系统可靠控制设计 [J].吉林大学学报: 信息科学版,2014,52(1): 65-70.LI Aichen,LI Xiangshan,JIAO Jianyu,et al.Reliable Control Design for Nonlinear Systems with Actuators Faults [J].Journal of Jilin University: Information Science Edition,2014,52(1): 65-70.

[6]MOHAND ARAB DJEZIRI,ROCHD MERZOUKI,BELKACEM OULD BOUAMAMA,et al.Fault Diagnosis and Fault-Tolerant Control of an Electric Vehicle Overactuated [J].IEEE Trans Vehicle Technology,2013,62(3): 986-994.

[7]SHAI A AROGETI,WANG Danwei,CHANG BOON LOW,et al.Fault Detection Isolation and Estimation in a Vehicle Steering System [J].IEEE Trans Industrial Electronics,2012,59(12): 4810-4820.

[8]WANG Rongrong,WANG Junmin.Fault-Tolerant Control with Active Fault Diagnosis for Four-Wheel Independently Driven Electric Ground Vehicles [J].IEEE Trans Vehicular Technology,2011,60(9): 4276-4287.

[9]HOK K NG,ROBERT H CHEN,JASON L SPEYER.A Vehicle Health Monitoring System Evaluated Experimentally on a Passenger Vehicle [J].IEEE Trans Control Systems Technology,2006,14(5): 854-870.

[10]陈则刚,袁信.基于证据论证的车辆组合导航系统的信息融合 [J].吉林大学学报: 信息科学版,2006,24(1): 36-41.CHEN Zegang,YUAN Xin.Information Fusion Methods Based on Evidential Theory for Vehicle Integrated Navigation System [J].Journal of Jilin University: Information Science Edition,2006,24(1): 36-41.

[11]廉智超,欧阳丹彤.基于模型检测的实时模型诊断方法 [J].吉林大学学报: 信息科学版,2007,45(6): 948-952.LIAN Zhichao,OUYANG Dantong.Real Time Model-Based Diagnostic Method Based on Model Checking [J].Journal of Jilin University: Information Science Edition,2007,45(6): 948-952.

[12]汤晓君,张进永,刘君华.基于多检测模型半导体气敏传感器故障诊断 [J].吉林大学学报: 信息科学版,2006,24(2): 126-130.TANG Xiaojun,ZHANG Jinyong,LIU Junhua.Fault Diagnosis for Semiconductor Gas Sensor Based on Multiple Measurement Model [J].Journal of Jilin University: Information Science Edition,2006,24(2): 126-130.

[13]余志生.汽车理论 [M].北京: 机械工业出版社,2009.YU Zhisheng.Automobile Theory [M].Beijing: China Machine Press,2009.

[14]GUO Konghui.A Unified Non-Steady Non-Linear Tire Model under Complex Wheel Motion Inputs Including Extreme Operating Conditions [J].SAE Review,2001,22(4): 395-402.

[15]郭孔辉.各向摩擦系数不同条件下轮胎力学特性的统一理论模型 [J].中国机械程,1996,7(4): 35-39.GUO Konghui.United Theory Model of Tire Mechanical Characteristic under Various Conditions of Different Friction Coefficients [J].China Mechanical Engineering,1996,7(4): 35-39.

[16]郭孔辉.汽车操纵动力学 [M].长春: 吉林科学技术出版社,1991.GUO Konghui.Vehicle Handling Dynamics [M].Changchun: Jilin Science & Technology Press,1991.

[17]DING S X.Model-Based Fault Diagnosis Techniques: Design Schemes,Algorithms,and Tools [M].Berlin,Germany: Springer,2008: 20-139.

(责任编辑： 刘东亮)

Fault Diagnosis and Reconfiguration for Vehicle Roll Rate Sensor

WANG Dejun,SONG Shiyao,WANG Xicong

(School of Communication Engineering,Jilin University,Changchun 130012,China)

Aiming at the vehicle roll rate sensor fault,a new model based method was proposed,focusing on fault diagnosis and fault reconfiguration.Comparing with the traditional method,an exact proof is given,which gets the strong robust residual,and the high high-precision signal of the faulty sensor.The multi-input-multi-output nonlinear system,which fulfills the Lipchitz Condition,could be took place by a equivalent model which is a one-dimension linear state equation with a model uncertainty,in the sensor fault diagnosis problem.The residual generator is designed by the classical observer theory,and through the eigenstructure assignment theory,a proof is addressed that the model uncertainty,actuator fault and disturbance could be perfectly decoupled from residual.The effectiveness of the result in testified by the 8-dof model in Simulink.

fault diagnosis; fault reconfiguration; model-based; Lipchitz; sensor; eigenstructure assignment

1671-5896(2015)02-0144-09

2014-04-02

国家自然科学基金重点资助项目(61034001)

王德军(1970— ),男,内蒙古通辽人,吉林大学副教授,硕士生导师,主要从事复杂系统故障诊断及容错控制研究,(Tel)86-13604422573(E-mail)djwang@jlu.edu.cn。

TP273

A