裂缝性储层渗透率张量定量预测方法

刘敬寿，戴俊生，邹 娟，杨海盟，汪必峰，周巨标

[1.中国石油大学(华东) 地球科学与技术学院，山东 青岛 266555； 2.中国石油 冀东油田分公司 勘探开发研究院，河北 唐山 063004； 3.中国石化 江苏油田分公司 安徽采油厂，安徽 天长 239300]

裂缝性储层渗透率张量定量预测方法

刘敬寿1，戴俊生1，邹 娟2，杨海盟1，汪必峰1，周巨标3

[1.中国石油大学(华东) 地球科学与技术学院，山东 青岛 266555； 2.中国石油 冀东油田分公司 勘探开发研究院，河北 唐山 063004； 3.中国石化 江苏油田分公司 安徽采油厂，安徽 天长 239300]

针对裂缝渗透率张量难以准确定量预测的问题，借助于古今岩石力学层产状的变化，预测裂缝的现今产状；以断裂力学中裂缝表面能以及岩石应变能理论为基础，预测现今裂缝的线密度；通过现今应力场数值模拟，计算三向挤压状态下裂缝的开度，进而确定现今裂缝的平行渗透率。利用裂缝的现今产状将静态坐标系与动态坐标系统一到大地坐标系中，建立了多组裂缝渗透率张量的定量预测模型，给出了渗透率主值、主值方向的计算公式，并且通过调整动态坐标系旋转角预测单元体内不同方向的渗透率。定义了表征渗透率各向异性的3个参数:裂缝渗透率极差比、渗透率突进系数和渗透率变异系数，定量评价裂缝渗透率的非均质性。以铜城断裂带东翼阜宁组二段储层为例，进行了裂缝渗透率张量预测工作。

渗透率张量；渗透率各向异性；定量预测；裂缝；铜城断裂带

在低渗透储层勘探开发过程中，裂缝是油气渗流的主要通道，裂缝渗透率的非均质性是影响油水流动方向的主控因素，裂缝性油气藏勘探开发的难点在于储层岩体中裂缝分布范围、发育程度的预测以及裂缝渗透率各向异性分析评价[1-4]。裂缝形成演化与古今地应力场演化密切相关[4-7]，其中，裂缝渗透率随有效应力变化表现出较强的应力敏感性[8-9]。因此，利用古今应力场数值模拟结果开展裂缝渗透率定量预测工作具有良好的理论基础，是一种比较可靠的裂缝定量预测方法。

在地下储层中，天然裂缝分布极为复杂，裂缝渗透率各向异性主要受裂缝产状、密度和开度等多种因素综合影响。在裂缝性油气藏动-静态相结合的建模方法中[10-11]，所预测的结果大都局限于定性评价裂缝的渗透率，并未考虑渗透率各向异性的特点。而传统数值模拟方法预测裂缝发育程度、分布范围时，采用向量形式表征裂缝的渗透率，但前提是大地坐标轴与渗透率主值方向相同，若平面渗透率主值方向与坐标轴方向有较大的差异，用简单向量形式表征渗透率可能在后期量化渗透率各向异性时出现较大的误差，难以符合油田合理高效开发的要求[1,12-14]。刘月田等[15]采用建立物理模型的方法量化裂缝性油藏的物性参数以及各向异性，具有较高的实用性和可行性。在本文中，笔者尝试将静态坐标系与动态坐标系统一到大地坐标系中，同时利用古今应力场数值模拟结果，建立一套实用完善的裂缝渗透率各向异性定量预测评价方法。

1 裂缝渗透率张量预测模型

1.1 现今裂缝产状预测

运用应力场数值模拟方法能够得到古裂缝产状[16-17]，而裂缝的形成发育主要受岩石力学层控制[18-20]。岩石力学层是指一套岩石力学行为相似或者岩石力学性质基本一致的岩层，岩石力学层一般但不总是岩性均一层[21]。因此，借助于古今岩石力学层的产状变化可以准确得到现今裂缝的产状：设裂缝形成时期所在平面的单位法向矢量为n′，倾角为α，倾向为β；现今裂缝面的单位法向矢量为n；古岩石力学层所在平面的法向矢量为p1，现今岩石力学层所在平面的法向矢量为p2，矢量p1与矢量p2所在平面的单位法向矢量为p。

矢量n′在大地坐标系中的3个分量为

(1)

矢量n与矢量n′的定量转换关系可表示为

(2)

式中，旋转矩阵T1可表示为

(3)

式中:(px，py，pz)为矢量p在大地坐标系中3个坐标轴的分量；ξ为矢量p1与矢量p2重合的旋转角，(°)。

1.2 建立裂缝渗透率预测模型

地下岩层在古应力场作用下破裂产生裂缝后，裂缝渗透率各向异性可以借助于适当的模型进行研究。通过建立微小单元体模型表征裂缝渗透率的各向异性。为了满足研究需要，认为单元体模型足够小，所有裂缝均能将其切穿。

前人在表征渗透率各向异性时，所建的坐标系通常是静态的[1,12-13]或把裂缝渗透率看做简单矢量的形式[12-13]，因此，很难准确地在平面内求取渗透率主值以及主值方向。本文通过静态坐标系与动态坐标系相结合的思路解决了这一问题。如图1所示，以裂缝为参照物建立静态坐标系(O-EFG)，静态坐标系中的三个坐标轴分别对应于裂缝面的法线方向(OE轴)、裂缝走向方向(OF轴)、裂缝面内垂直于裂缝走向线的方向(OG轴)。以大地坐标为参照物建立动态坐标系(O-XYZ)，定义θ为水平面内OX轴与正东方向的夹角，即动态坐标系的旋转角，通过调整θ的大小，求取裂缝在动态坐标系中不同方向的渗透率；定义OX轴位于北东向时θ为负值，位于南东向时θ为正值；动态坐标系中OZ轴表示铅直方向。

1.3 现今裂缝的线密度-开度预测

构造应力场数值模拟方法进行储层构造裂缝预测具有良好的理论基础。国内学者戴俊生等[6，13，22-23]从影响储层构造裂缝形成与发育的地质因素入手，通过对裂缝形成时期的古应力场数值模拟，结合岩石破裂准则以及单井裂缝描述成果，利用岩石应变能理论、裂缝表面能理论以及能量守恒定律，建立了古今应力场与储层构造裂缝参数之间的定量关系；在现今地应力场中一般不再产生新的裂缝[6,13,23]，裂缝的线密度、产状及组系特征具有继承性，但在现今3向挤压应力影响下，已存的裂缝会出现一定程度的闭合，渗流能力变差。Willis-Richards等[24]和Jing等[25-26]同时考虑了正应力及剪应力存在时对裂缝开度的影响，得出现今地应力场改造后裂缝开度的计算公式为

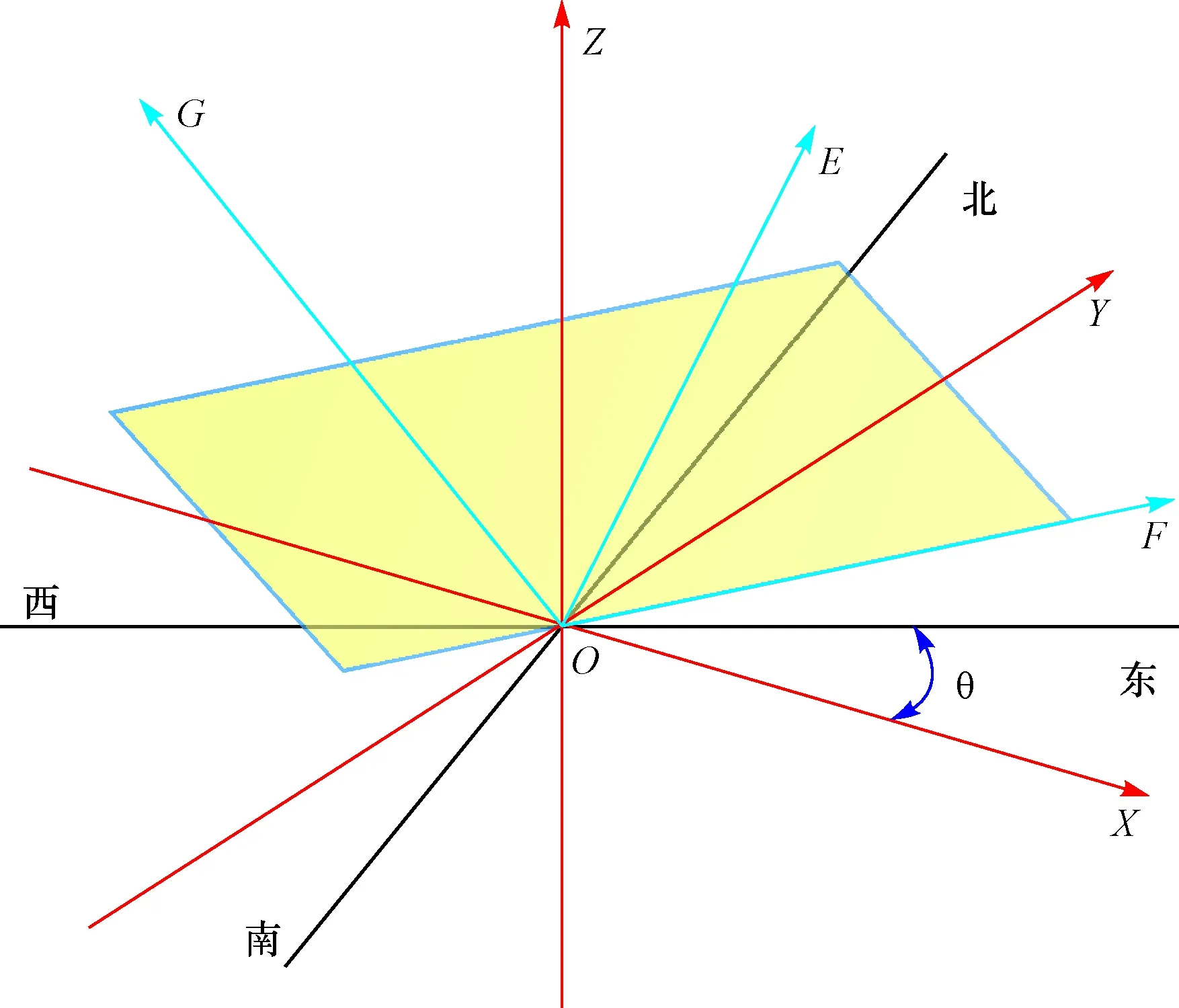
图1 静态坐标系与动态坐标系关系示意图Fig.1 Schematic diagram showing relations between static and dynamic coordinate systems

(4)

在古今应力场数值模拟的基础上，求取单元体内现今裂缝的线密度以及开度，单组裂缝的平行渗透率K可以表示为

(5)

式中:Dlf为单组裂缝的线密度，条/m。

2 动态坐标系中裂缝渗透率张量预测

2.1 单组裂缝渗透率张量预测

设裂缝的渗透率张量为K，则其在坐标系O-XYZ中的表达式可表示为

(6)

同理，渗透率张量K在坐标系O-EFG中的表达式可表示为

(7)

在静态坐标系中，每个单元体内单组裂缝的渗透率张量KEFG可表示为

(8)

由公式(6)—(8)可以得到

(9)

其中静态坐标系转换为动态坐标系的旋转矩阵T2可表示为

(10)

在动态坐标系中，单元体内每组裂缝的渗透率张量KXYZ可表示为

(11)

式中，Cθ和Dθ满足

(12)

2.2 多组裂缝渗透率张量预测

在复杂的地质条件下，储层裂缝经历多期构造应力场演化，每组裂缝的产状、线密度和开度往往不同，依据公式(5)、公式(11)及公式(12)，单元体内发育多组裂缝时，渗透率的主值方向θmax可以表示为

(13)

在单元体内裂缝渗透率主值方向上，渗透率主值大小Kmax可以表示为

(14)

式中:k为单元体内裂缝的组数；bi为第i组裂缝的开度，m；Dlfi为第i组裂缝的线密度，条/m；(nxi，nyi，nzi)分别为第i组裂缝面的单位法向向量在大地坐标系中3个坐标轴的分量，可由公式(1)—(3)得到。

3 裂缝渗透率各向异性评价参数

裂缝的渗透率具有强烈的各向异性，参考储层渗透率非均质性参数的定义公式[30-32]，提出了评价裂缝渗透率各向异性的3个参数——渗透率极差比(τb)、突进系数(τk)和变异系数(τy)。针对不同地区裂缝的发育规律，选取具有代表性的非均质性参数，当单元体之间不同方向的裂缝渗透率变化规律一致时，选用渗透率极差比(τb)便能较好的评价渗透率非均质性；当单元体之间不同方向的裂缝渗透率变化规律不一致时，宜采用突进系数(τk)或变异系数(τy)评价渗透率的非均质性。

渗透率极差比(τb)表征的是井点附近渗透率最大值与最小值的比值。渗透率极差比的变化范围为1～∞，τb数值越大非均质性越强。

(15)

式中：Kmax为单元体内渗透率最大值，10-3μm2；Kmin为单元体内渗透率最小值，10-3μm2。

渗透率突进系数(τk)表征的是一定井段内渗透率最大值与其平均值的比值。同样，τk值变化范围为1～∞，τk数值越大非均质性越强。

(16)

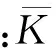
渗透率变异系数(τy)是一个数理统计的概念，用于度量单元体内不同方向的渗透率值相对于平均值的离散程度。数值变化范围为0～∞，τy数值越大非均质性越强。

(17)

式中：Kθi为单元体内θi方向的渗透率值，10-3μm2；n为对应的单元体内，计算的n个方向裂缝渗透率的数目。

4 实例应用

4.1 区域地质概况

铜城断裂带地处江苏省金湖县境内，构造上位于苏北盆地东台坳陷金湖凹陷中，是划分龙岗-汊涧次凹的盆地内区带级右旋走滑断层，南部交汇于金湖凹陷的边界——杨村断层，向北消失于铜城地区(图2)。在平面上，铜城断层表现为一条线状主位移带，主干断层两侧雁列断层发育；剖面上，断层陡立；空间中，主断层倾向东西摇摆，出现“丝带效应”[34-35]。该地区主力产油层为阜二段(阜宁组二段)，储层物性差，岩性以低渗透粉砂岩为主，裂缝在油气渗流中起至关重要的作用。

阜二段储层主要造缝时期为吴堡期，该时期铜城地区主要受近南北向的拉张应力，通过岩心裂缝定向分析[36]，铜城断裂带东翼阜二段主要发育北东东向和南东东向两组剪切裂缝，裂缝倾角以垂直缝及高角度斜交缝为主。

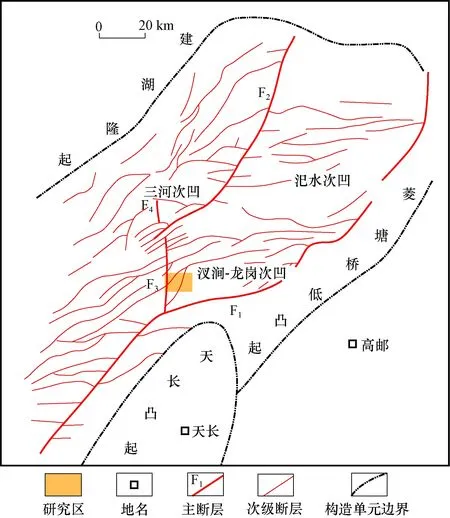
图2 铜城断裂带东翼构造位置(据文献[33]中修改)Fig.2 Structural location of the east flank of the Tongcheng fault belt(modified based on reference[33])F1.杨村断层；F2.石港断层；F3.铜城断层；F4.崔庄断层

4.2 渗透率张量预测

在数值模拟中，合理的古今应力场分布是储层裂缝参数准确预测的前提，其中现今应力场又是裂缝现今开度预测关键[6,13,23]。以铜城断裂带阜二段底面构造图为基础，利用平衡剖面技术恢复阜二段古构造形态，根据小层对比图，在ANSYS有限元模拟软件中建立阜二段砂泥互层的地质模型(厚度120 m)；对模型网格划分后生成96 000余个单元体，借助于岩石力学实验结果(表1)，对不同属性的单元体赋予不同的岩石力学参数，建立力学模型；将古今应力、应变数据导入裂缝参数计算模型，并以多井岩心裂缝参数为约束，通过不断地反演、拟合，确定在地质模型的南北边界施加4.5 MPa的拉张应力，东西边界施加1.5 MPa的拉张应力，定义模型自身的重量，并在底面施加Z方向约束、南北边界施加线性约束，以保证有限元计算结果收敛。数值模拟结果显示，铜城断裂带东翼阜二段储层均已达到岩石张剪破裂条件，裂缝普遍发育。铜城断裂带东翼裂缝线密度为2.85～4.68 条/m，岩心判断[36]两组裂缝线密度比值为3 ∶2，断层附近以及构造低部位裂缝的线密度为高值；在现今三向挤压应力场中，裂缝开度为(20～44)×10-6m，约是古开度的0.2～0.3倍。

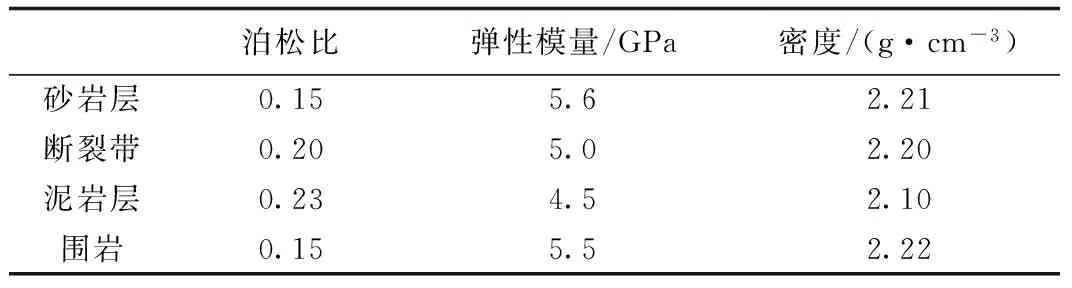
表1 铜城断裂带阜二段应力场数值模拟力学参数Table 1 Mechanical parameters for stress field simulation of Fu-2 Memberin the Tongcheng fault belt

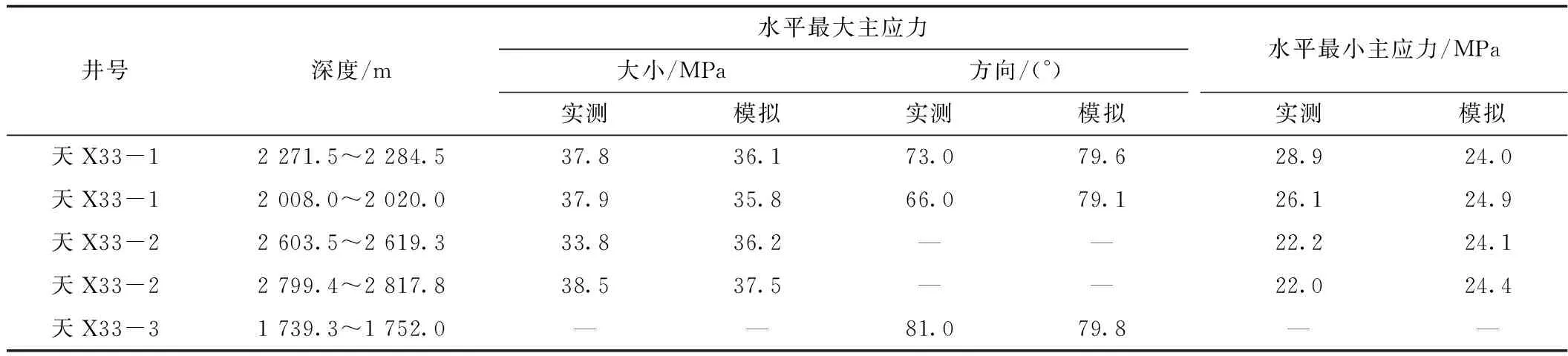
表2 铜城断裂带东翼实测结果与现今应力场数值模拟对比Table 2 Comparison between the measured and present stress field simulation in the east flank of the Tongcheng fault belt

综合研究区的岩心声速实验、古地磁定向实验、压裂资料以及微地震监测结果，并参考邻区的地应力信息，确定现今水平最大主应力为NEE 79°挤压应力，大小为37 MPa；水平最小主应力为NNW 349°的挤压应力，大小为25 MPa；定义模型自身的重量，在地质模型的底面施加Z方向的约束使有限元模型计算收敛。对比现今应力场模拟结果与铜城断裂带东翼部分井位监测计算结果，发现两者吻合较好(表2)，由此可认为现今裂缝参数的预测结果能够较准确地反映储层裂缝的实际情况。

在预测古裂缝的产状、开度以及线密度的基础上，使用公式(1)—(17)中的算法，通过不断地调整动态坐标系中θ值的大小，能够得到井点附近不同方向上的裂缝渗透率数值(图3)。由图得出，在井点附近裂缝的渗透率优势方向为近东西向；在靠近断层的井点，由于裂缝开度大，裂缝的渗透率主值大。这一结论同样符合断层-裂缝系统的发育规律[13,23,37-43]。

如图3所示，水平面内井点不同方向的渗透率变化为单峰单谷型，峰-谷间渗透率规律性的变大或者减小，不同方向的渗透率呈似椭圆形分布；如图4所示，通过拟合不同单元体中3个渗透率各向异性参数，得出τb与τk,τy呈良好的正相关关系，即3个参数在

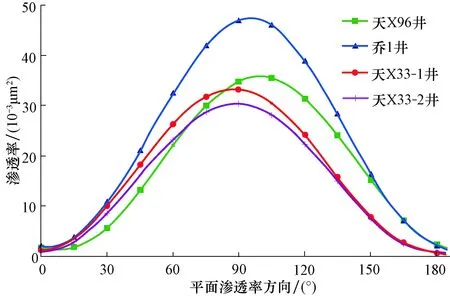
图3 铜城断裂带阜二段井点不同方向上裂缝渗透率大小Fig.3 Fraccture permeability at different directions of wells in the Fu-2 Member of the Tongcheng fault belt

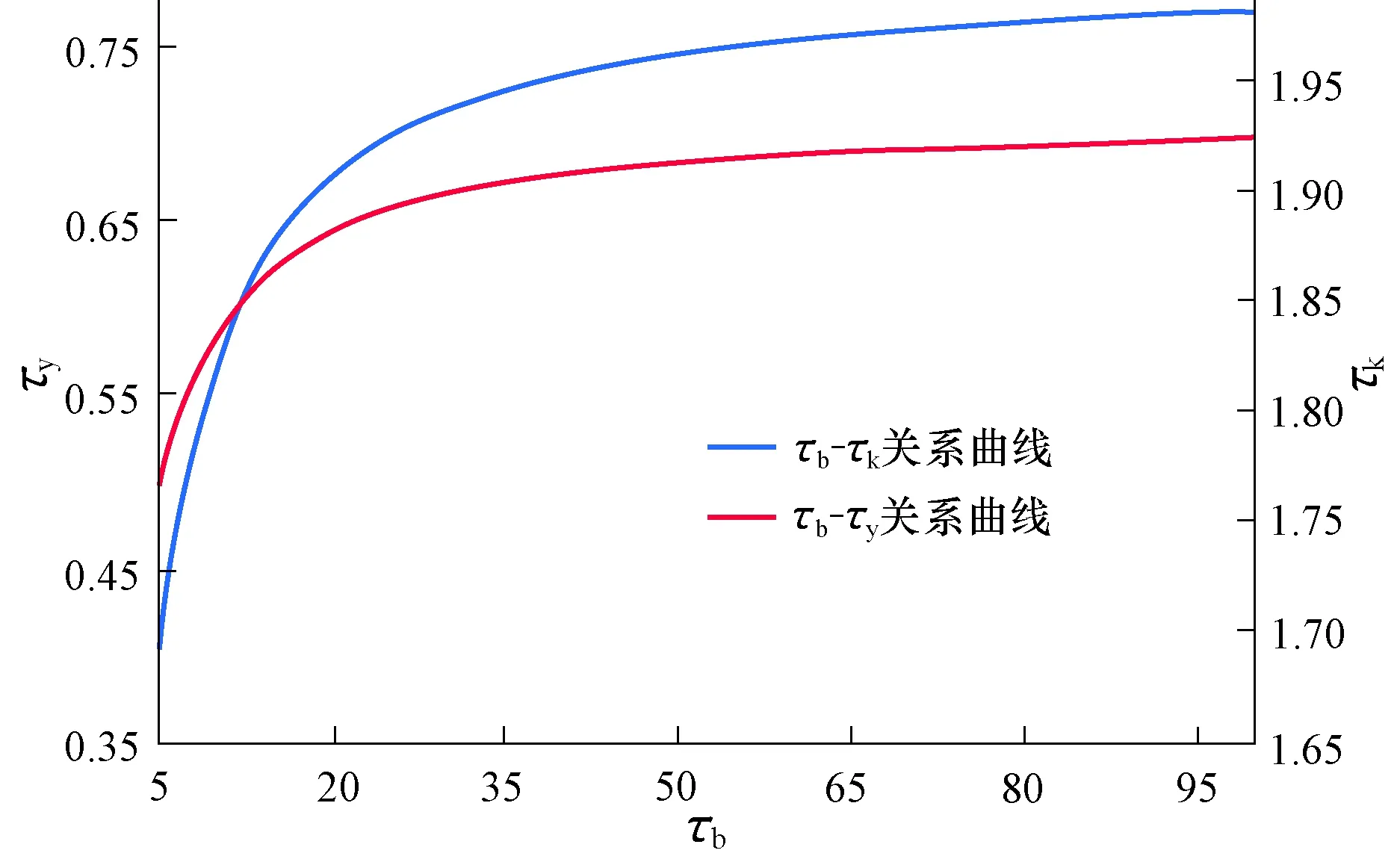
图4 铜城断裂带阜二段单元体间τb与τy,τk拟合曲线Fig.4 Fitting curves of τb,τy,and τk in different unit bodies in the Fu-2 Member of the Tongcheng fault belt

图5 铜城断裂带阜二段平面最大渗透率主值分布Fig.5 Plane distribution of the maximum permeability in the Fu-2 Member of the Tongcheng fault belt

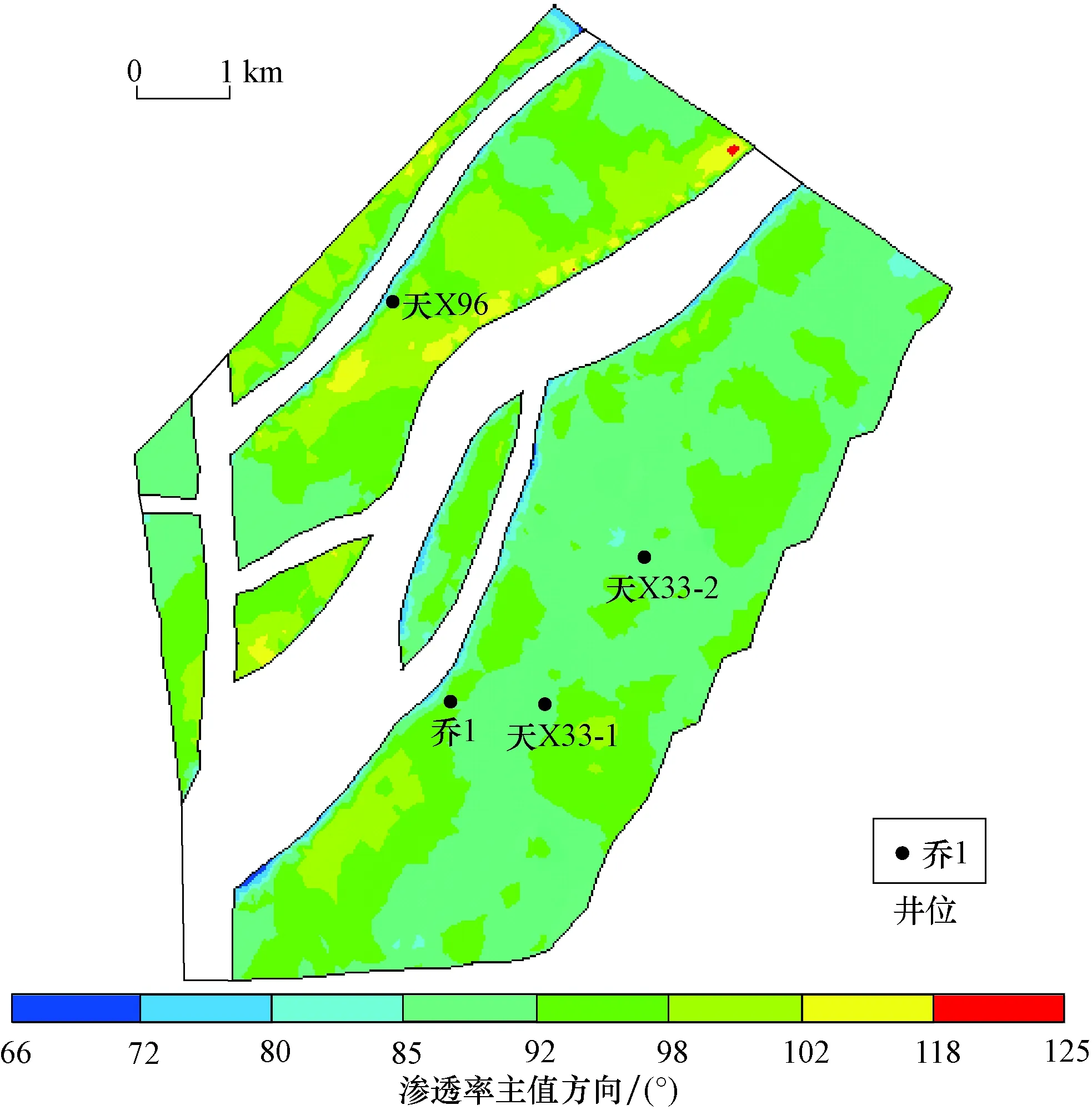
图6 铜城断裂带阜二段平面最大渗透率主值方向分布Fig.6 Direction plane distribution of the maximum permeability in the Fu-2 Member of the Tongcheng fault belt

反应单元体渗透率各向异性的趋势是基本一致的，但渗透率极差比(τb)(变化范围5.5～99.5)能更好反应不同单元体之间的差异性。故采用裂缝渗透率主值、渗透率主值方向和渗透率极差比3个参数定量评价工区目的层位裂缝渗透率的非均质性。

水平面内，阜二段储层渗透率主值集中分布在(10～70)×10-3μm2，在构造低部位为低值，在断层附近的构造高部位为高值，随着与断层距离的增大，渗透率急剧减小(图5)。天96断块渗透率主值方向以北东东向为主，天33断块最大渗透率主值方向以南东东向为主(图6)，这也与乔1井、天X96井、天X33-1井以及天X33-2井动态开发过程中油气的优势渗流方向相吻合。

如图7所示，阜二段储层渗透率极差比(τb)预测结果表明，在靠近断层的构造高部位，裂缝渗透率极差比为低值。在构造低部位，渗透率极差比为高值。

5 结论

1) 利用现今裂缝产状，通过定义静态坐标系与动态坐标系建立裂缝渗透率计算模型，调整动态坐标系的旋转角，定量分析裂缝渗透率各向异性，提出了单组-多组裂缝渗透率主值以及渗透率主值方向的计算方法。

2) 在水平面内，裂缝渗透率主值与单元体内发育的裂缝组数、每组裂缝的开度、线密度以及裂缝的产状有关；渗透率主值方向与单元体内发育的裂缝组数、每组裂缝的开度、线密度以及裂缝的走向有关，与裂缝的倾角无关。

图7 铜城断裂带阜二段平面渗透率极差比分布Fig.7 Plane distribution of ratio of the maximum and minimum value in the permeability of the Fu-2 Member of the Tongcheng fault belt

3) 定义了评价裂缝非均质性参数提出并应用渗透率主值、渗透率主值方向以及各向异性参数定量评价裂缝渗透率非均质性。通过建立裂缝渗透率计算模型预测裂缝平面的渗透率张量，利用该思路同样可以评价任意剖面渗透率的非均质性。

4) 在靠近断层的井点，裂缝的渗透率主值大，随着与断层距离的增大，渗透率急剧减小。在构造低部位，渗透率极差比为高值。

[1] 刘月田,丁祖鹏,屈亚光,等.油藏裂缝方向表征及渗透率各向异性参数计算[J].石油学报,2011,32(5):842-846. Liu Yuetian,Ding Zupeng,Qu Yaguang,et al.The characterization of fracture orientation and the calculation of anisotropic permeability parameters of reservoirs[J].Acta Petrolei Sinica,2011,32(5):842-846.

[2] 赵向原,曾联波,靳宝光,等.裂缝性低渗透砂岩油藏合理注水压力——以鄂尔多斯盆地安塞油田王窑区为例[J].石油与天然气地质,2015,36(5): 855-861. Zhao Xiangyuan,Zeng Lianbo,Jin Baoguang,et al.Discussion on optimal injection pressure of fractured low-permeability sandstone reservoirs-A case study from Wangyao block in Ansai oilfield,Ordos Basin[J].Oil & Gas Geology,2015,36(5): 855-861.

[3] Abdelkader Kouider El Ouahed,Djebbar Tiab,Amine Mazouzi.Application of artificial intelligence to characterize naturally fractured zones in Haeei Meeeannd Oil Field,Algeriai[J].Journal of Petroleum Science and Engineering,2005,49(3/4):122-141.

[4] 周新桂,张林炎,屈雪峰,等.沿河湾探区低渗透储层构造裂缝特征及分布规律定量预测[J].石油学报,2009,30(2):195-200. Zhou Xingui,Zhang Linyan,Qu Xuefeng,et al.Characteristics and quantitative prediction of distribution laws of tectonic fractures of low-permeability reservoirs in Yanhewan area[J].Acta Petrolei Sinica,2009,30(2):195-200.

[5] Titeux M,Janson X,Srinivasan S,et al.Facies distribution in collapsed carbonate karsts:a mechanical approach[A].AAPG Annual Convention & Exhibition[C].Houston:2011.(Poster).

[6] 季宗镇,戴俊生,汪必峰.地应力与构造裂缝参数间的定量关系[J].石油学报,2010,33(1):68-72. Ji Zongzhen,Dai Junsheng,Wang Bifeng.Quantitative relationship between crustal stress and parameters of tectonic fracture[J].Acta Petrolei Sinica,2010,33(1):68-72.

[7] 曾联波,漆家福,王成刚,等.构造应力对裂缝形成与流体流动的影响[J].地学前缘,2008,15(3):292-298. Zeng Lianbo,Qi Jiafu,Wang Chenggang,et al.The influence of tectonic stress on fracture formation and fluid flow[J].Earth Science Frontiers,2008,15(3):292-298.

[8] 王文环,彭缓缓,李光泉,等.大庆低渗透油藏注水动态裂缝开启机理及有效调整对策[J].石油与天然气地质,2015,36(5): 842-847. Wang Wenhuan,Peng Huanhuan,Li Guangquan,et al.Opening mechanism of dynamic fractures caused by water injection and effective adjustments in low permeability reservoirs,Daqing oilfield in Songliao Basin.Oil & Gas Geology,2015,36(5): 842-847.

[9] 王珂,戴俊生,张宏国,等.裂缝性储层应力敏感性数值模拟:以库车坳陷克深气田为例[J].石油学报,2014,1(1):123-133. Wang Ke,Dai Junsheng,Zhang Hongguo,et al.Numerical simulation of fractured reservoir stress sensitivity:a case from Kuqa depression Keshen gas field[J].Acta Petrolei Sinica,2014,1(1):123-133.

[10] Gurpinar O,Kalbus J,List D F.Numerical modeling of a large,naturally fractured oil complex[R].SPE 59061,2000.

[11] Abbaszadeh M,Corbett C,Broetz R,et al.Development of an integrated reservoir model for a naturally fractured volcanic reservoir in China[R].SPE 59439,2000.

[12] 冯阵东,戴俊生,王霞田,等.不同坐标系中裂缝渗透率的定量计算[J].石油学报,2010,32(1):135-139. Feng Zhendong,Dai Junsheng,Wang Xiatian,et al.Quantitative calculation of the tectonic fracture permeability in different coordinate systems[J].Acta Petrolei Sinica,2010,32(1):135-139.

[13] 季宗镇,戴俊生,汪必峰,等.构造裂缝多参数定量计算模型[J].中国石油大学学报:自然科学版,2010,34(1):24-28. Ji Zongzhen,Dai Junsheng,Wang Bifeng,et al.Multi-parameter quantitative calculation model for tectonic fracture [J].Journal of China University of Petroleum:Natural Science Edition,2010,34(1):24-28.

[14] 单娴,姚军.基于渗透率张量的各向异性油藏两相渗流数值模拟[J].中国石油大学学报:自然科学版,2011,35(2):101-106. Shan Xian,Yao Jun.Numerical simulation for twophase flow in heterogeneous reservoirs based on full permeability tensor[J].Journal of China University of Petroleum:Edition of Natural Science,2011,35(2):101-106.

[15] 刘月田,刘剑,丁祖鹏,等.非均质各向异性裂缝油藏物理模型制作方法[J].石油学报,2013,34(6):1119-1125. Liu Yuetian,Liu Jian,Ding Zupeng,et al.The method of making physical model for heterogeneous and anisotropic fractured reservoirs[J].Acta Petrolei Sinica,2013,34(6):1119-1125.

[16] 文世鹏,李德同.储层构造裂缝数值模拟技术[J].石油大学学报:自然科学版,1996,20(5):17-24. Wen Shipeng,Li Detong.Numerical simulation technology for structural fracture of reservoir[J].Journal of China University of Petroleum:Natural Science Edition,1996,20(5):17-24.

[17] 周新桂,张林炎,范昆.含油气盆地低渗透储层构造裂缝定量预测方法和实例[J].天然气地球科学,2007,18(3):328-333. Zhou Xingui,Zhang Linyan,Fan Kun.Methods for quantitative prediction of tectonic fractures in compact reservoirs in petroliferous basins and a case study[J].Natural Gas Geoscience,2007,18(3):328-333.

[18] Bai T,Pollard,David D.Closely space fractures in layered rocks:initiation mechanism and propagation kinematics[J].Journal of structural geology,2000,22(10):1409-1425.

[19] 康志江,赵艳艳,张允,等.缝洞型碳酸盐岩油藏数值模拟技术与应用[J].石油与天然气地质,2014,35(6): 944-949. Kang Zhijiang,Zhao Yanyan,Zhang Yun,et al.Numerical simulation technology and its application to fractured-vuggy carbonate reservoirs[J].Oil & Gas Geology,2014,35(6): 944-949.

[20] Chad A,Underwood M L,Cooke J A,et al.Stratigraphic controls on vertical fracture patterns in Silarian dolomite,northeastern Wisconsin[J].AAPG Bulletin,2003,87(1):121-142.

[21] 曾联波.低渗透砂岩储层裂缝的形成与分布[M].北京:科学出版社,2008:103-104. Zeng Lianbo.Formation and distribution of fractures in low-permeability sandstone reservoirs[M].Beijing:Science Press,2008:103-104.

[22] 戴俊生,冯建伟,李明,等.砂泥岩间互地层裂缝延伸规律探讨[J].地学前缘,2011,18(2):277-283. Dai Junsheng,Feng Jianwei,Li ming,et al.Discussion on the extension law of structural fracture in sand-mud interbed formation[J].Earth Science Frontiers,2011,18(2):277-283.

[23] 冯建伟,戴俊生,马占荣,等.低渗透砂岩裂缝参数与应力场关系理论模型[J].石油学报,2011,32(4):664-671. Feng Jianwei,Dai Junsheng,Ma Zhanrong,et al.The theoretical model between fracture parameters and stress field of low-permeability sandstones[J].Acta Petrolei Sinica,2011,32(4):664-671.

[24] Willis-Richards J,Watanabe K,Takahashi H.Progress toward a stochastic rock mechanics model of engineered geothermal systems[J].Journal of Geophysical Research:Solid Earth (1978-2012),1996,101(B8):17481-17496.

[25] Jing Z,Willis-Richards J,Watanabe K,et al.A new 3D stochastic model for HDR geothermal reservoir in fractured crystalline rock[C].Proceedings of the 4th International HDR Forum,Strasbourg,1998.

[26] Jing Z,Willis-Richards J,Watanabe K,et al.A three-dimensional stochastic rock mechanics model of engineered geothermal systems in fractured crystalline rock[J].Journal of Geophysical Research:Solid Earth (1978-2012),2000,105(B10):23663-23679.

[27] Durham W B,Bonner B P.Self-propping and fluid flow in slightly offset joints at high effective pressures[J].Journal of Geophysical Research:Solid Earth (1978-2012),1994,99(B5):9391-9399.

[28] Chen Z,Naryan S P,Yang Z,et al.An experimental investigation of hydraulic behavior of fractures and joints in granitic rock[J].International Journal of Rock Mechanics and Mining Science,2000,37(7):1061-1071.

[29] 秦积舜.变围压条件下低渗砂岩储层渗透率变化规律研究[J].西安石油学院学报:自然科学版,2002,17(4):28-31. Qin Jishun.Variation of the permeability of the low-permeability sandstone reservoir under variable confined pressure[J].Journal of Xi'an Shiyou University:Natural Science Edition,2002,17(4):28-31.

[30] Choi K,Jackson M D,Hampson G,et al.Impact of het erogeneity on flow in fluvial-deltaic reservoirs:Im plications for the giant ACG field,South Caspian Basin[J].Society of Petroleum Engineers,2007:3214-3229.

[31] Roy B,Anno P,Gurch M.Imaging oil-sand reservoir hetero geneities using wide-angle prestack seismic inversion[J].Leading Edge,2008,27(9):1192-1201.

[32] Kwon S I,Sung W M,Hu H D G,et al.Characterization of reservoir heterogeneity using in verse model equipped with parallel genetic algorithm[J].Energy Sources,2007,29(9):823-838.

[33] 叶绍东.金湖凹陷铜城断层构造特征与油气成藏[J].地质力学学报,2012,18 (2):187-194. Ye Shaodong.Structural characteristics of Tongcheng fault and hydrocarbon accumulation in Jinhu sag[J].Journal of Geomechanics,2012,18(2):187-194.

[34] 能源,漆家福,张春峰,等.金湖凹陷断裂特征及其石油地质意义[J].大地构造与成矿学,2012,36 (1):16-23. Neng Yuan,Qi Jiafu,Zhang Chunfeng,et al.Structural features of the Jinhu sag in the Subei Basin and its petroleum geological significance[J].Geotectonica Et Metallogenia,2012,36 (1):16-23.

[35] 能源,漆家福,张春峰,等.金湖凹陷石港断层构造演化及油气聚集特征[J].石油学报,2009,30(5):667-671. Neng Yuan,Qi Jiafu,Zhang Chunfeng,et al.Structural evolution of Shigang fault and features of hydrocarbon accumulation in Jinhu Sag[J].Acta Petrolei Sinica,2009,30(5),667-671.

[36] 刘敬寿,戴俊生,王珂,等.斜井岩心裂缝产状校正方法及其应用[J].石油学报，2015，36(1) :67-73. Liu Jingshou,Dai Junsheng,Wang Ke,et al.An approach to correct the attitudes of fracture for deviated borehole in core and its application[J].Acta Petrolei Sinica,2015,36(1) :67-73.

[37] 张克银.川西孝泉-新场地区须家河组四段裂缝分布特征[J].石油实验地质,2014,36(4):398-404. Zhang Keyin.Fracture distribution characteristics of 4th member of Xujiahe Formation in Xiaoquan-Xinchang area,western Sichuan[J].Petroleum Geology & Experiment,2014,36(4):398-404.

[38] 杨勉,徐梓洋,杨柏松,等.贝尔凹陷基岩潜山致密储层裂缝分布预测[J].石油与天然气地质,2014,35(2): 253-257. Yang Mian,Xu Ziyang,Yang Baisong,et al.Fracture prediction of bedrock buried hill tight reservoirs in Beier Depression.Oil & Gas Geology,2014,35(2): 253-257.

[39] 梁积伟,李宗杰,刘昊伟,等.塔里木盆地塔河油田S108井区奥陶系一间房组裂缝性储层研究[J].石油实验地质,2010,32(5):447-452. Liang Jiwei,Li Zongjie,Liu Haowei,et al.Characteristics of fracture reservoir of Ordovician Yijianfang Formation in S108 area of Tahe Oilfield,Tarim Basin[J].Petroleum Geology & Experiment,2010,32(5):447-452.

[40] 国殿斌，徐怀民，梁国胜，等.东濮凹陷北部盐间泥岩裂缝储层预测技术研究[J].油气地质与采收率，2014，21(5)：53-56. Guo Dianbin,Xu Huaimin,Liang Guosheng，et al.Practical technology of inter-salt mudstone fracture prediction in the north of Dongpu depression[J].Petroleum Geology and Recovery Efficiency，2014，21(5)：53-56.

[41] Hennings P,Allwardt P,Paul P,et al.Relationship between fractures,fault zones,stress,and reservoir productivity in the Suban gas field,Sumatra,Indonesia[J].AAPG bulletin,2012,96(4):753-772.

[42] 陈伟,吴智平,侯峰,等.断裂带内部结构特征及其与油气运聚关系[J].石油学报,2010,31(5):774-780. Wu Wei,Wu Zhiping,Hou Feng,et al.Internal structures of fault zones and their relationship with hydrocarbon migration and accumulation[J].Acta Petrolei Sinica,2010,31(5):774-780.

[43] 谢景彬，龙国清，田昌炳，等.特低渗透砂岩油藏动态裂缝成因及对注水开发的影响——以安塞油田王窑区长6油组为例[J].油气地质与采收率，2015，22(3)：106-110. Xie Jingbin,Long Guoqing,Tian Changbing,et al.Genetic mechanism of dynamic fracture and its influence on water flooding development in extra-low permeability sandstone reservoir：a case of Chang6 member in Wangyao area，Ansai oilfield[J].Petroleum Geology and Recovery Efficiency，2015，22(3)：106-110.

(编辑 张玉银)

Quantitative prediction of permeability tensor of fractured reservoirs

Liu Jingshou1,Dai Junsheng1,Zou Juan2,Yang Haimeng1,Wang Bifeng1,Zhou Jubiao3

(1.SchoolofGeosciences,ChinaUniversityofPetroleum,Qingdao,Shandong266555,China;2.Exploration&DevelopmentResearchInstitute,JidongOilFieldCompany,PetroChina,Tangshan,Hebei063004,China;3.AnhuiOilProductionPlantofJiangsuOilfield,SINOPEC,Tianchang,Anhui239300,China)

Aiming at difficulties to quantitatively predict fracture permeability tensor,present fracture occurrence was predicted based on occurrence change of rock mechanical layers.Present liner density of fracture was predicted based on the facture surface energy theory and the rock strain energy theory of fracture mechanics.According to the results of present stress field numerical simulation,fracture opening was calculated in three direction extrusion stress state and then present facture parallel permeability was determined.By using present fracture attitudes,static and dynamic coordinate systems were unified into geodetic coordinate system,a quantitative prediction model of multi-group fracture permeability tensors was constructed,formula for calculating the principal value of permeability and main value direction were given,and permeability at different directions in unit body was predicted by adjusting the dynamic coordinate system rotation angle.Three parameters,the ratio of the maximum and minimum value of the permeability,heterogeneity coefficient of permeability and variation coefficient of permeability,were defined to quantitatively evaluate fracture permeability heterogeneity.Fu-2 Member fractured reservoir in the eastern flank of Tongcheng fault belt was taken as an example to predict fracture permeability tensor.

permeability tensor,permeability anisotropy,quantitative prediction,fracture,Tongcheng fault belt

2014-10-29;

2015-08-11。

刘敬寿，男，(1989—)，硕士研究生，储层裂缝。E-mail：liujingshou@126.com。

国家科技重大专项(2011ZX05042-001)；中央高校基本科研业务费专项资金资助项目(13CX02033A)。

0253-9985(2015)06-1022-08

10.11743/ogg20150618

TE122.2

A