火星任务中星上原时τ与TCG的相对论变换

潘军洋，谢 懿，2，3

(1.南京大学 天文与空间科学学院，南京 210093；2.上海市 空间导航与定位技术重点实验室，上海 200030；3.南京大学 现代天文与天体物理教育部重点实验室，南京 210093)

火星任务中星上原时τ与TCG的相对论变换

潘军洋1，谢 懿1，2，3

(1.南京大学 天文与空间科学学院，南京 210093；2.上海市 空间导航与定位技术重点实验室，上海 200030；3.南京大学 现代天文与天体物理教育部重点实验室，南京 210093)

爱因斯坦的广义相对论已成为当今深空探测任务中一部分，为此将在研究环火星探测器星载钟原时τ与地球质心坐标时(TCG)的变换中应用相对论变换关系，将τ与地球相关联的局部时间尺度联系起来，从而扩展了之前关于τ与太阳系质心坐标时(TCB)相对论变换的工作(TCB是应用于整个太阳系的全局坐标时)。研究发现τ和TCG的差在经历一年的时间后可达到0.2 s量级。为了区分相对论变换中各种效应的贡献，用数值方法计算了太阳、八大行星、三个大质量小行星以及探测器的贡献。发现在精确到1 μs量级下，相对论变换必须包括太阳、金星、月球、火星、木星、土星的引力影响以及探测器和地球的速度影响。

参考系；时间；数值方法；空间探测器

0 引 言

随着现代技术的极大发展，爱因斯坦的广义相对论(GR)已成为深空探测任务中的一部分。它早已不再局限于理论天文学和物理学层面而进入了应用和工程领域[1]。由于GR引起的效应在一些空间任务的无线电信号传输中很明显地显露出来[2-3]，这些效应为GR提供了最强的约束条件[2]。

GR的一个重要概念就是抛弃牛顿绝对时空观中的绝对时间。在GR下存在不同种类的时间：原时和坐标时[4]。理想时钟的读数为原时τ，这是一个可观测量并只属于时钟自身。坐标时不能被直接观测到，但它们可用作自然天体、人造天体和光线运动方程中的自变量。坐标时和原时通过四维空时间隔相联系，这一特征取决于时钟的运动学和动力学因素。它极大地改变了时钟同步和时间变换的方式[1]。

在火星和其他行星探测任务中，星载钟和地面上时钟的同步对于控制、导航和科学探测是至关重要的。根据国际天文学联合会(IAU)决议[5]，同步需要完成两个中间步骤。第一步是τ和太阳系质心坐标时(TCB)的相对论变换；第二步，TCB将被转换为地球质心坐标时(TCG)，TCG是属于地球局部参考系的坐标时。之后TCG可以很方便地转换为地球上的其他时标如地球时(TT)，国际原子时(TAI)，协调世界时(UTC)。

以“萤火1号”任务[6-7]作为中国未来火星探测的一个技术案例，已有一些工作致力于研究第一步转换[8-9]。文献[10]的作者(2012)通过分析和数值方法发现这个转换的两个主要因素：太阳的引力场和探测器在质心参考系中的速度。这两个因素的共同贡献可达到每年几个亚秒的量级[10]。文献[11]的作者(2013)将钟差考虑在内，发现如果校准后的星载钟精度高于10-6～10-5秒每年(取决于钟差类型)，那么τ和TCB之间的相对论变换需要仔细处理[11]。

在这篇文章中，作为之前工作的延伸，将主要讨论τ和TCG的相对论变换，也就是把第一步和第二步联合起来。在第2节中，将在IAU决议下[5]计算类“萤火1号”任务的τ和TCG的相对论变换，并使该变换以历表所采用的变量为引数(详见附录A)。在第3节中，将用数值方法计算该变换并给出不同来源的贡献。在第4节中给出结论与讨论。

1 τ与TCG的转换关系

根据IAU决议[5]，航天器上星载钟原时τ与t≡TCB的关系在一阶后牛顿近似下为

(1)

这里定义ε≡1/c，忽略各天体引力场中非球对称部分。下标“s”代表航天器，下标“A”代表需要考虑引力场作用的天体。对于T≡TCG，它和t的转换关系为

t-T=

(2)

其中:E代表地球。将方程(1)与方程(2)相加即得τ与TCG的相对论变换

(3)

为求得τ-T的值，其中一个可行的方法是利用历表提供的太阳系天体相对于太阳系内的位置和速度数据数值积分方程(3)等式右边。然而实现这一计算并不方便，因为等式右边的时间变量为TCB而不是质心力学时(TDB)。TDB是太阳系星历表中广泛应用的独立变量。因此，出于应用考虑，使方程(3)等式右边以TDB为变量是必要的。利用TCB和TDB的关系[12]，得到新的关系

τ-T=∑3i=1ΔTi+∑7j=1ΔTj′+O(ε2J(A)n，ε4，L2B)

(4)

等式右边以TDB为变量。ΔTi(i=1，2，3)与方程(3)中各项对应。ΔT1相当于τ和t的相对论变换部分；ΔT2和ΔT3来自t和T的相对论变换。方程(4)的细节和完整表达式在附录A中给出。在下一章中，我们将用数值方法研究这个方程中的每个成分。值得注意的是，方程(4)考虑了TCB和TDB的差异，这在之前的工作中是被忽略的[10-11]。

2 对τ-T的数值分析

按照文献[11]的作者(2013)假设的情况，设想一个探测器从2017-01-01 00∶00∶00.0000(TDB)到2017-01-18 01 00∶00∶00.0000(TDB)时间内环绕火星运行。在文章的余下部分将全部以该时间起点为零点。该探测器轨道相对于火星赤道倾角为5°。远火点高度为8万km，近火点高度为800 km，轨道周期约3.2天。为求得方程(4)的值，我们采用辛普森求积公式[13]，利用DE405历表给出的数据进行数值积分。即天体的位置和速度数据来自DE405历表，探测器轨道由Einstein-Infeld-Hoffmann方程[14]通过7阶Runge-Kutta方法[13]数值积分得到，步长为其开普勒周期的1%。计算过程中计入的提供引力贡献的天体有：太阳、八大行星、月球和三个大质量小行星：谷神星、智神星、灶神星。

图1显示了ΔT1[方程(A.8)]，ΔT2[方程(A.9)]和ΔT1+ΔT2的贡献。ΔT1对应τ-t成分，为负值且可达到-0.3s/年。ΔT2对应t-T成分，它可达到0.5s/年。因此ΔT1+ΔT2可达到约0.2 s/年的数量级。从理论和应用考虑，一个重要的问题是区分贡献的不同来源。图2显示了由各个天体的引力效应和探测器的运动学效应提供的贡献。如果精确到±1 μs并忽略绝对值小于1 μs的项，会发现在ΔT1中只需要考虑太阳，火星，木星，土星和探测器速度的贡献。同样地，图3除右下角外显示了各个来源对ΔT2的贡献。同样精确到1 μs，需要考虑的项为由太阳、金星、月球、木星、土星引力和地球速度产生的影响。

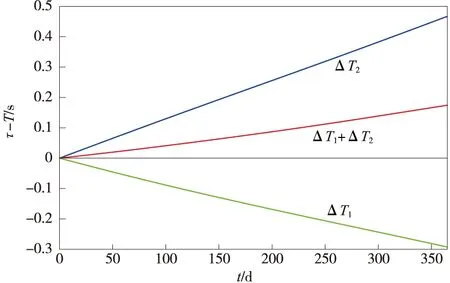
图1 ΔT1、ΔT2以及ΔT1+ΔT2随时间(天)的变化曲线。其数学表达式见附录方程(A.8)和(A，9) Fig.1 Curves of ΔT1， ΔT2 and ΔT1+ΔT2. Their mathematical descriptions are given in Eqs. (A.8) and (A.9)

ΔT3项[附录方程(A.10)]在探测器通信链路末端，它取决于观测者位置。如果考虑一个地面跟踪站，ΔT3将受到地球自转的强烈影响，数量级可达2 μs/d。图3右下角ΔT3曲线是假设跟踪站位于中国北京得到的。

图2 ΔT1中各种效应的贡献随时间(天)的变化曲线，包括：太阳 (Sun)、水星(Mercury)、金星(Venus)、地球(Earth)、月球(Moon)、火星(Mars)、谷神星(Ceres)、智神星(Pallas)、灶神星(Vesta)、木星(Jupiter)、土星(Saturn)、天王星(Uranus)、海王星(Neptune)以及探测器的速度Fig.2 In ΔT1， contributions from the Sun， Mercury， Venus， Earth， the Moon， Mars， Ceres， Pallas，Vesta， Jupiter， Saturn， Uranus， Neptune and the velocity of the spacecraft

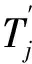
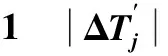
表(j=1，…，7)的贡献最大值

注:包括太阳 (Sun)、水星(Mercury)、金星(Venus)、地球(Earth)、月球(Moon)、火星(Mars)、谷神星(Ceres)、智神星(Pallas)、灶神星(Vesta)、木星(Jupiter)、土星(Saturn)、天王星(Uranus)、海王星(Neptune)以及太阳速度和其加速度点积vs·as、地球速度和其加速度点积vE·aE。

3 结论与讨论

在这篇文章中，以类“萤火1号”任务作为例子，研究了星载钟原时τ和TCG的相对论变换，扩展了先前关于τ和TCB相对论变换的工作。发现τ和TCG的差可达0.2 s/年。如果精确到1 μs，这一相对论变换必须考虑太阳、金星、月球、火星、木星和土星的引力影响以及地球和探测器的速度影响。

4 附录A:τ-T：以TDB为变量

作为历表的时间引数，TDB由下式[12]由TCB得到：

TDB=TCB-LB×(JDTCB-T0)×

(A.1)

其中：JDTCB为TCB的儒略日；T0=2 443 144.537 25；LB=1.550 519 768×10-8；TDB0=-6.55×10-5s为定义好的常量。喷气推进实验室将儒略日作为星历表时间引数，因此将上式表为儒略日形式，有

(A.2)

其中，JDTDB0=TDB0/(86 400s)=-7.581 018 518 5×10-10。由此可得

(A.3)

其中，gJD(JDTDB)≡LB×(JDTDB-T0)-(1+LB)JDTDB0。

有关JDTCB的方程可展开为

(A.4)

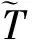
(A.5)

(A.6)

联合方程(A.5)和(A.6)，最终将得到

(A.7)

其中

(A.8)

(A.9)

(A.10)

(A.11)

(A.12)

(A.13)

(A.14)

(A.15)

(A.16)

(A.17)

[1] Nelson R. Relativistic time transfer in the vicinity of the Earth and in the solar system[J]. Metrologia， 2011，48(4):171-180.

[2] Bertotti B， Iess L， Tortora P. A test of general relativity using radio links with the Cassini spacecraft[J]. Nature， 2003，425(6956):374-376．

[3] Ni Jensen J， Weaver G. The in-flight frequency behavior of two ultra-stable oscillators onboard the new horizons spacecraft[C]∥Proc. Annual Precise Time and Time Interval (PTTI) Meeting， 39th， Long Beach， CA: [s.n.], 2007:79-93．

[4] Misner C， Thorne K， Wheeler J. Gravitation [M]. San Francisco: W.H. Freeman and Co.， 1973:393-398.

[5] Soffel M， Klioner S， Petit G， et al. The IAU 2000 resolutions for astrometry， celestial mechanics， and metrology in the relativistic framework: explanatory supplement[J]. AJ， 2003，126(6):2687-2706．

[6] Ping J， Qian Z， Hong X， et al. Brief Introduction About Chinese Martian Mission Yinghuo-1[C]∥Lunar and Planetary Science Conference， 41st. The Woodlands， Texas: [s.n.], 2010:1060.

[7] Ping J， Shang K， Jian N， et al. Brief introduction of YINGHUO-1 Mars orbiter and open-loop tracking techniques[C]∥Proceedings of the Asia-Pacific International Conference on Gravitation and Astrophysics， 9th. Wuhan: [s.n.], 2010:225-232.

[8] Deng X， Xie Y. The effect of f(T) gravity on an interplanetary clock and its time transfer link[J]. Research in Astron. Astrophys. 2013，13(10):1225-1230．

[9] Deng X， Xie Y. Yukawa effects on the clock onboard a drag-free satellite[J]. MNRAS， 2013，431(4):3236-3239．

[10] Deng X. The transformation betweenτand TCB for deep space missions under IAU resolutions[J]. Research in Astron. Astrophys.， 2012，12(6):703-712．

[11] Pan J， Xie Y. Relativistic transformation betweenτand TCB for Mars missions: fourier analysis on its accessibility with clock offset [J]. Research in Astron. Astrophys.， 2013，13(11):1358-1362．

[12] Petit G， Luzum B， IERS Conventions[M].(IERS Technical Note; 36) Bundesamt für Kartographie und Geodäsie， 2010:151-152．

[13] Stoer J， Bulirsch R. Introduction to Numerical Analysis [M]. New York: Springer， 2002:491-498．

[14] Einstein A， Infeld L， Hoffmann B. The gravitational equations and the problem of motion[J]. Annals of Mathematics， 1938，39(1):65-100． 作者简介： 谢懿(1981—)，男，博士，副教授，主要研究方向：基本天文学。 通信地址：江苏省南京市汉口路22号南京大学天文与空间科学学院(210093) 电话：(025)89681230 E-mail:yixie@nju.edu.cn

[责任编辑：宋宏]

Relativistic Transformation between the Proper Timeτand TCG for Mars Missions

PAN Junyang1， XIE Yi1，2，3

(1.Department of Astronomy， Nanjing University， Nanjing 210093， China； 2.Shanghai Key Laboratory of Space Navigation and Position Techniques， Shanghai 200030， China; 3.Key Laboratory of Modern Astronomy and Astrophysics， Nanjing University， Ministry of Education， Nanjing 210093， China)

Considering the fact that the general theory of relativity has become a part of deep space missions， we investigate the relativistic transformation between the proper time of an onboard clockτand the geocentric coordinate time (TCG) for Mars missions. By connectingτwith this local timescale associated with the Earth， we extend previous works which focus on the transformation between τ and the barycentric coordinate time (TCB). (TCB is the global coordinate time for the whole solar system.) For practical convenience， the relation betweenτand TCG is recast to directly depend on quantities which can be read from ephemerides. We find that the difference between τ and TCG can reach the level of about 0∶2 seconds in a year. To distinguish various sources in the transformation， we numerically calculate the contributions caused by the Sun， eight planets， three large asteroids and the spacecraft. It is found that if the threshold of 1 microsecond is adopted， this transformation must include effects due to the Sun， Venus， the Moon， Mars， Jupiter， Saturn and the velocities of the spacecraft and Earth．

reference systems；time；numerical method；space vehicles

2015-01-01

2015-02-18

国家自然科学基金资助项目(J1210039)；上海市空间导航与定位技术重点实验室基金(14DZ2276100)

P129

A

2095-7777(2015)01-0069-06

10.15982/j.issn.2095-7777.2015.01.010