附着小天体的最优制导控制方法

江秀强，陶婷，杨威，李爽

(1.南京航空航天大学 航天学院，南京 210016；2. 南京航空航天大学 航天新技术实验室，南京 210016)

附着小天体的最优制导控制方法

江秀强1，2，陶婷1，2，杨威1，2，李爽1，2

(1.南京航空航天大学 航天学院，南京 210016；2. 南京航空航天大学 航天新技术实验室，南京 210016)

以小天体伴飞附着任务为工程背景，针对探测器在小天体复杂弱引力场条件下附着这一难题，研究了最优制导控制策略。首先，考虑在小天体极区实施附着任务，建立并简化动力学模型，给出约束条件和基于时间-燃耗最优的混合性能指标要求。然后，采用相平面法设计了最优制导律，利用极限环设计最优开关控制律；同时，采用高斯伪谱法把附着小天体的最优制导问题转化成非线性规划问题，利用Matlab/GPOPS优化工具包求取最优数值解。最后，加入已有的基于矢量测量的自主光学导航模块构建GNC仿真回路，对两种最优制导控制策略进行仿真验证。结果表明：两种制导控制策略都能满足任务要求，但基于相平面法得到的最优制导控制具有一定风险，而基于高斯伪谱法得到的最优制导控制精度更高、燃耗更少，适于工程应用。

小天体；附着最优制导；相平面法；高斯伪谱法

0 引 言

小天体探测拓展了人类探索和利用空间资源的视野，有助于科学家研究太阳系的形成与演化。近年来一些国家和航天组织相继实施了自己的小天体探测任务。NASA在1996年发射的近地小行星交会探测器NEAR于2000年成功进入绕飞小行星Eros的任务轨道，获取了目标小行星的形状体积、质量、地表特征和自旋状态等参数，并于2001年2月12日通过事先规划好的五次减速制动成功着陆Eros小行星，成为第一个成功软着陆小行星的探测器[1-2]。日本宇宙航空研究开发机构(JAXA)于2003年发射的“隼鸟”(Hayabusa)探测器于2006年飞抵距离“糸川”小行星20 km的预定任务轨道，获取了“糸川”小行星的高精度三维地形图。探测器在光学系统制导下垂直下降，并最终成功登陆“糸川”小行星，成为第一个通过自主导航控制成功着陆小行星的探测器[3-4]。欧洲航天局(ESA)的“罗塞塔”(Rosetta)探测器于2004年发射，于2014年11月12日释放名为“菲莱”(Philae)的探测器成功降落在“丘留莫夫-格拉西缅科”彗星的彗核上并将进行采样返回[5-6]。小天体探测已成为深空探测的一大热点。

随着NEAR、Hayabusa、Rosetta等小天体探测任务的实施，着陆小行星的相关技术引起了国内外学者们的关注。Furfaro等(2013)[7]基于高阶滑模控制理论提出了小行星精确着陆的多滑模制导方法，该方法对于无模型有界扰动下具有一定鲁棒性。Zhang等(2012)[8]结合光学自主导航算法，给出着陆小天体的滑模变结构制导策略。但这些扰动的界难以事先获知，这类方法难以付诸实施。Lan等(2014)[9]以安全、精确附着为目标，提出了一种基于时间约束的附着控制方法，将着陆误差分解为位置误差和视线角误差，分别设计控制律使得有限时间内视线角误差稳定在原点附近，位置误差收敛于零附近。崔平远和崔祜涛等(2008—2012)研究了着陆小行星的特点和光学导航与制导方法[10-12]。龚胜平和李俊峰等(2011)研究了小天体伴飞的常推力控制方法，并以编号为1996FG3的小行星为例做了仿真验证[13]。李爽等(2005—2009)研究了着陆小行星的自主GNC技术，针对由于目标小行星的各种物理参数和运动信息不能精确获取而导致着陆小行星的动力学模型中存在不确定性这一问题，设计了软着陆小行星的光学导航、PD制导、滑模变结构制导和自主GNC方案[14-17]。在此基础上，本文研究讨论附着小天体的最优制导控制方法。分别采用相平面法和高斯伪谱法，发展基于时间-燃耗最优的附着小天体制导控制律。

1 附着小行星的最优制导问题描述

[14-17]给出的附着系统动力学模型

(1)

上述动力学方程x，y通道存在耦合项，由于小天体的自旋速度很小、加之小天体的引力作用很弱，相对于探测器的速度和推力大小而言，可以忽略上述小项的影响，附着动力学方程可以简化为[14-17]

(2)

为了保证上述简化的合理性，采用在小天体的极区实施附着，附着制导的三轴目标位置和速度即为零[15，18]。

以xl通道为例，单一通道的动力学方程可写为

(3)

由于附着任务具有一定的时间和燃耗限制，给出时间-燃耗最优性能指标

(4)

其中：ct为时间加权系数，则哈密尔顿函数可以构造为

(5)

为了保证时间燃耗最优，根据极小值原理应使选取合适的u(t)哈密尔顿函数H的值最小，即

(6)

最优控制律

(7)

协状态方程

(8)

受探测器所安装的推力器的限制，其控制力加速度(推力加速度)满足约束

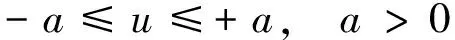
(9)

探测器通过长时间的伴飞，可以获取目标小天体的地形地貌、引力场和运行参数等准确数据，据此可确定附着任务起始点和目标点的状态，设状态量X=[x，y，z]T，即确定了问题的初末条件

(10)

2 基于相平面法的最优制导控制

相平面法是基于传统直接法思想的一种经典方法，也是工程中常用的。采用相平面法需求出三轴推力的正负开关线，而正关线和负关线方程是由角点条件和贯截条件来确定的。为了求出u(t)和X(t)的关系以便组成状态反馈系统，需将状态方程的解求出。分u=-a，u=+a，u=0三种情况进行讨论：

1)当u(t)=-a时，状态方程为

(11)

2)当u(t)=a时，状态方程为

(12)

3)当u(t)=0时，状态方程为

(13)

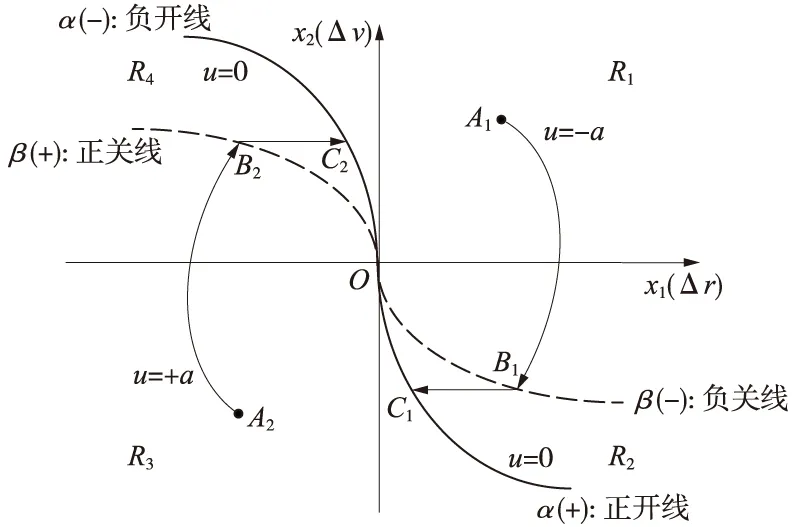
图1 相平面示意图Fig.1 Sketch of phase plane

由前面的推导过程结合图1可得

负开线方程

(14)

正开线方程

(15)

下面确定负关线β(-):u(t)=-a⟹u(t)=0。要确定负关线方程，就必须确定B1的轨迹。由于控制力u(t)只在tB1，tC1发生切换，所以在负关点B1和正开点C1处λ2(t)条件满足

(16)

结合前式λ2(t)=c2-c1t可得

(17)

弧段C1O的终点条件为

(18)

由于到达终点的时间tf是待定的(附着时间自由)，则有

(19)

(20)

设tf-tC1=τ，则有

(21)

(22)

(23)

将x2(tC1)，λ2(tC1)代入(23)式中，并用λ1=c1代换得

(24)

在弧段B1C1上，由于u(t)=a=0，相轨迹匀速从负关点B1运动到正开点C1，则有

(25)

(26)

(27)

由拐点条件知：

(28)

则有

(29)

由式(15)～(17)、(25)、(26)、(29)可得负关线方程

(30)

同理可得正关线方程

(31)

负关线方程

(32)

正关线方程

(33)

考虑到工程实际应用，需要将上述制导指令调制成推力器的最优开关控制信号，引入极限环实现这一最优控制。设电磁阀的门限值为d，电磁阀滞宽为δ。如图2所示，由于极限环的存在，开关曲线方程为

(34)

图2 极限环最优控制示意图Fig.2 Sketch of limit cycle optimization control

从开关曲线方程及上面的曲线轨迹中，可以很容易地得到极限环的宽度为L=2d，而A点的纵坐标的2倍代表着极限环的高度W=2Ay。通过求取A(Ax，Ay)，B(Ax，-Ay)可确定极限环的宽度。

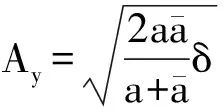
于是，整个相空间可以分为三个区域(见式(36))：

(36)

3 基于高斯伪谱法的最优制导控制

由于协状态对初值猜测很敏感，故基于极大值原理的间接优化理论在最优制导控制问题求解中往往过程繁杂、效率低下。下面采用高斯伪谱法来求解附着小天体的最优制导控制指令。

本文所定义的附着小天体的最优制导控制问题是一个终端时刻可动的最优问题，按照高斯伪谱法的步骤，首先将优化问题的时间域t∈[t0，tf]，映射到区间τ∈[-1，1]，映射函数为

(37)

取t0=0，则上式可以简化为

(38)

(39)

(40)

(41)

(42)

对式(39)求导并结合式(38)，可以得到

(43)

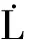
(44)

其中：k=1，2，…，N;i=0，1，…，N。由此，式(9)、(10)所示约束可以转化为

(45)

由式(2)，动力学约束可以表示为

(46)

式(4)所示目标函数可表示为

(47)

至此，附着小天体的最优制导控制问题被转化成了一个多约束的参数优化问题，转换过程如图3所示。

在MATLAB环境下编程，上述转换过程采用GPOPS优化工具包进行，非线性规划问题(nonlinearprogramingproblem,NLP)的求解器采用SNOPT软件包，最后同样将解得的最优制导指令调制成推力器的开关控制信号。

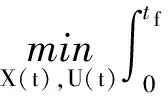
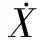
φ(X(t0),X(tf))=0

h(X(t),U(t))≤0h

↓

↓

ρ={X0,…,XN;U1,…,UN}

↓

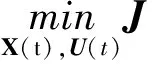
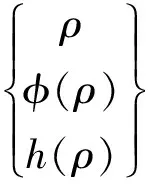
图3 优化问题转换过程

Fig.3 Optimization problem transformation process

4 仿真分析

为贴近实际、完整地反映制导控制效果，采用文献[17](2007)所述的基于矢量测量的自主光学导航模块，与本文所述制导控制构成一个完整的GNC回路，如图4所示。

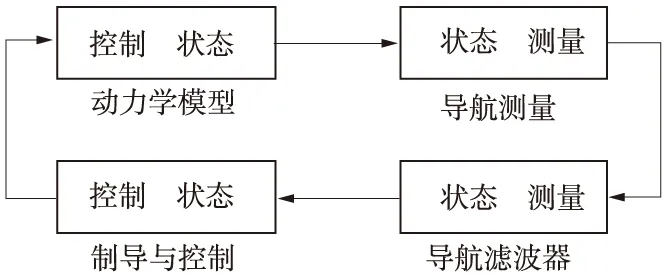
图4 附着小天体的GNC仿真框图Fig.4 Sketch of GNC for spacecraft attaches to a small body

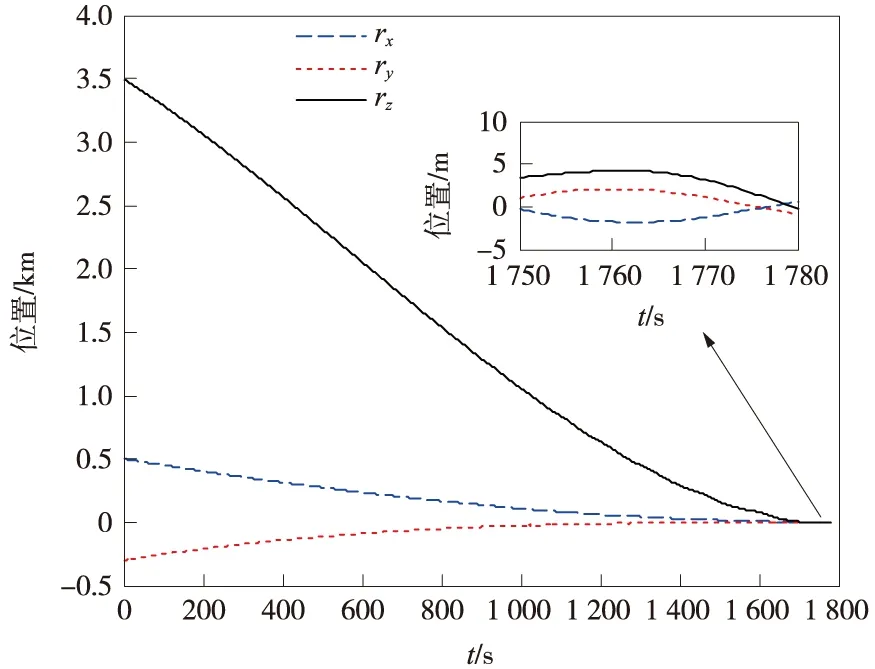
图5 基于相平面法的附着位置曲线Fig.5 Landing position curve: phase plane method

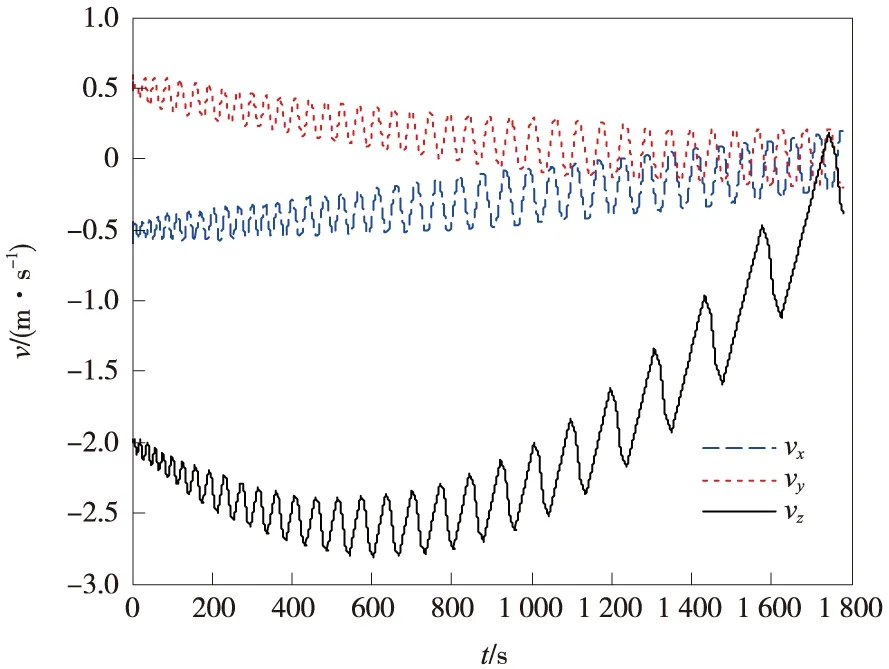
图6 基于相平面法的附着速度曲线Fig.6 Landing velocity curve: phase plane method

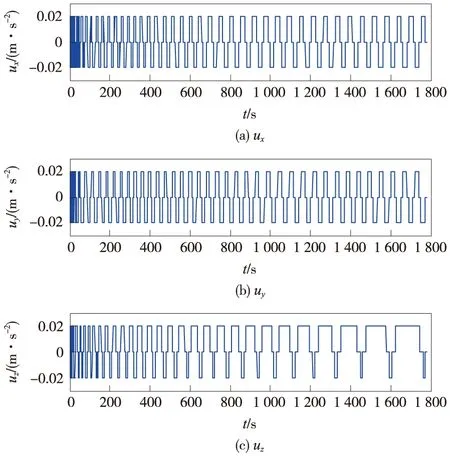
图7 基于相平面法的三轴喷气控制加速度Fig.7 Tri-axis jet control acceleration: phase plane method

图8 基于高斯伪谱法的附着位置曲线Fig.8 Landing position curve: gauss pseudospectral method

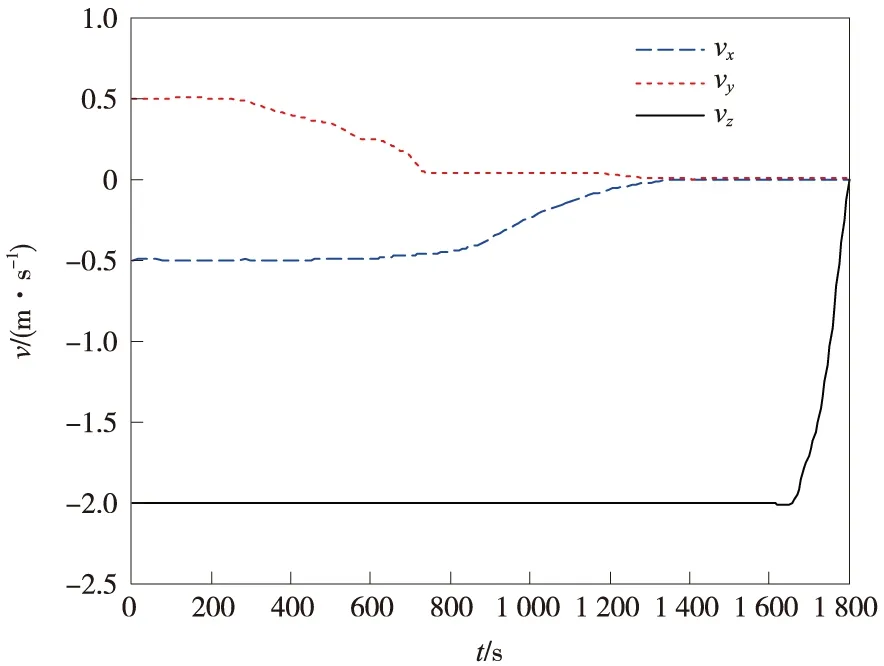
图9 基于高斯伪谱法的附着速度曲线Fig.9 Landing velocity curve: gauss pseudospectral method

图10 基于高斯伪谱法的三轴喷气控制加速度Fig.10 Tri-axis control acceleration: gauss pseudospectral method

图11 控制代价曲线Fig.11 Control cost curve

Table 1 Comparison of terminal position errors and velocity errors

分量对比末端位置误差/m末端速度误差/(m·s-1)PPMGPMPPMGPMx方向067013020002y方向-099-016-021-002z方向-015-005-039-003合误差120021049004

从仿真结果可以看出，采用两种方法都能控制探测器安全附着。但是采用相平面法的最优制导律在控制过程中，推力器会处于频繁的开关状态，使得速度在收敛过程中不断波动，在末端仍然具有明显的速度和位置偏差，尤其是0.49 m/s的速度误差已经接近给定的附着速度误差指标上限0.5 m/s，这些都会给探测器的附着过程引入风险，而且还会多消耗工质。而采用高斯伪谱法的最优制导控制过程平缓，三轴推力器的开关控制频度和工作时间明显减少，这使得附着过程的燃耗降低了一半以上，并且末端位置和速度的控制精度提高了一个数量级，利于在小天体上安全精确附着。而制导误差与导航误差[17]已经非常接近，表明导航精度是限制制导精度进一步提升的主要因素。虽然比前一种方法多用了19 s的时间，但这个小段时间很容易在任务起始点被消除。

5 结束语

本文分别基于相平面法和高斯伪谱法给出了附着小天体极区的两种最优制导控制策略。其中，采用经典的相平面法给出了制导控制律的显式表达式；基于高斯伪谱法的最优制导给出了求解过程，由MATLAB/GPOPS优化工具包求得数值解；最后将制导指令调制成推力器的开关信号。通过引入文献[17](2007)的基于矢量测量的自主光学导航模块，构建GNC仿真回路，对两种最优制导控制策略进行了仿真验证。结果表明，采用高斯伪谱法不仅运算时间短、收敛性好，而且制导过程平滑度、末端精度和控制代价都全面优于经典的相平面法，适合于在线实时最优制导控制。基于相平面法得到的最优制导则可以为高斯伪谱法的最优制导求解提供一定的初值参考。

参考文献

[1] Veverka J， Farquhar B， Robinson M， et al. The landing of the NEAR-Shoemaker spacecraft on asteroid 433 Eros[J]. Nature， 2001，413(6854):390-393.

[2] Nelson R， Whittenburg K， Holdridge M. 433 Eros landing-development of near shoemaker’s controlled descent sequence[C]∥15th Annual AIAA/USU Conference on Small Satellites， SSC 01-11， [S.l.]: AIAA， 2001.

[3] Yano H， Kubota T， Miyamoto H， et al. Touchdown of the Hayabusa spacecraft at the Muses Sea on Itokawa[J]. Science， 2006，312(5778):1350-1353.

[4] Kubota T， Hashimoto T， Sawai S， et al. An autonomous navigation and guidance system for MUSES-C asteroid landing[J]. Acta Astronautica， 2003，52(2):125-131.

[5] Ferri P. Mission operations for the new rosetta[J]. Acta Astronautica, 2006，58(2):105-111.

[6] Ulameca S. Rosetta lander-philae: implications of an alternative mission[J]. Acta Astronautica, 2006，58(8):435-441.

[7] Furfaro R， Cersosimo D， Wibben D R. Asteroid precision landing via multiple sliding surfaces guidance techniques[J]. Journal of Guidance， Control， and Dynamics， 2013，36(4):1075-1092.

[8] Zhang Z X， Wang W D， Li L T， et al. Robust sliding mode guidance and control for soft landing on small bodies[J]. Journal of the Franklin Institute， 2012，349(2):493-509.

[9] Lan Q， Li S， Yang J， et al. Finite-time control for soft landing on an asteroid based on line-of-sight angle[J]. Journal of the Franklin Institute， 2014，351(1):383-398.

[10] 崔平远，朱圣英，崔祜涛.小天体软着陆自主光学导航与制导方法研究[J].宇航学报，2009，30(6):2159-2164. [Cui P Y， Zhu S Y， Cui H T. Autonomous optical navigation and guide method for soft landing on small bodies[J]. Journal of Astronautics， 2009，30(6):2159-2164.]

[11] 崔平远，朱圣英，崔祜涛.小天体自主软着陆脉冲机动控制方法研究[J]. 宇航学报，2008，29(2):121-126. [Cui P Y， Zhu S Y， Cui H T. Autonomous impulse maneuver control method for soft landing on small bodies[J]. Journal of Astronautics， 2008，29(2):121-126.]

[12] 高艾，崔平远，崔祜涛.基于约束规划的小天体接近段鲁棒制导控制方法[J].系统工程与电子技术，2012，34(5):989-995. [Gao A， Cui P Y， Cui H T. Robust guidance and control algorithms for small-body proximity operations based on constrained programming[J]. Systems Engineering and Electronics， 2012，34(5):989-995.]

[13] 龚胜平，李俊峰，宝音贺西.小天体伴飞的常推力控制[J].中国科学: 物理学力学 天文学，2011，41(10):1224-1229. [Gong S P， Li J F， Baoyin H X. Utilization of constant low thrust for control of spacecraft near asteroid[J]. Scientia Sinica Phys， Mech & Astron， 2011，41(10):1224-1229.]

[14] 李爽，崔平远.着陆小行星的滑模变结构控制[J].宇航学报，2005， 26(6):807-812. [Li S， Cui P Y. Variable structure with sliding-mode control for landing on asteroids[J]. Journal of Astronautics， 2005，26(6): 807-812.]

[15] 李爽，崔祜涛，崔平远.着陆小天体的自主GNC技术[J].宇航学报，2006，27(1):21-26. [Li S， Cui H T， Cui P Y. Autonomous GNC technology for landing on small bodies[J]. Journal of Astronautics， 2006，27(1):21-26.]

[16] Li S， Zhang L. Autonomous navigation and guidance scheme for precise and safe planetary landing[J]. Aircraft Engineering and Aerospace Technology: An International Journal， 2009，81(6):516-521．

[17] 李爽.基于光学测量的相对导航方法及在星际着陆中的应用研究[D].哈尔滨：哈尔滨工业大学博士论文，2007. [Li S. Study on optical measurement based relative navigation and its application in planetary landing[D]. Harbin: Harbin Institute of Technology， 2007.]

[18] 姜宇，宝音贺西.强不规则天体引力场中的动力学研究进展[J].深空探测学报，2014，1(4):250-261. [Jiang Y， Baoyin H X. A Survey on dynamics in the gravitational field of irregular celestial body[J]. Journal of Deep Space Exploration， 2014，1(4):250-261.] 作者简介： 江秀强(1987—)，男，博士研究生，主要研究方向：深空探测总体技术、精确着陆/打击的导航制导与轨迹优化技术。 通信地址：江苏省南京市御道街29号南京航空航天大学航天学院(210016) 电话：(025)84896521-6211 E-mail：jiangxq@nuaa.edu.cn 李爽(1978—)，男，工学博士，教授，主要研究方向：航天器动力学与控制、深空探测、航天技术新概念等。 通信地址：江苏省南京市御道街29号南京航空航天大学航天学院(210016) 电话：(025)84896521-6211 E-mail：lishuang@nuaa.edu.cn

[责任编辑：宋宏]

Optimal Guidance Control Strategies for Spacecraft Attaches to A Small Body

JIANG Xiuqiang1，2， TAO Ting1，2， YANG Wei1，2， LI Shuang1，2

(1.College of Astronautics， Nanjing University of Aeronautics and Astronautics， Nanjing 210016， China;2.Space New Technology Laboratory， Nanjing University of Aeronautics and Astronautics， Nanjing 210016， China)

The issue of spacecraft attaching to a small body with complex weak gravitation field is challenging. In this paper， two optimal guidance control strategies are addressed with the mission background of accompany flight and attaching to a small body. First， taking the attaching mission in polar area of small body into consideration， dynamics model is constructed and simplified， as well as the constraints and time-fuel integrated optimal performance index is described. Secondly， phase plane method (PPM) is used to design optimal guidance， and optimal on-off control is given by limit circle. Next， Gauss pseudospectral method (GPM) is utilized to transform optimal guidance problem into nonlinear program (NLP) problem， and MATLAB/GPOPS optimal tool software package is utilized to obtain the numerical solution of guidance. Finally， the vector measurement based autonomous optical navigation given in the previous work is introduced to GNC simulation loop， and the two optimal guidance control strategies are verified. Simulation results show that both of them meet the requirement of mission， but the phase plane method based optimal guidance control is a little risky， while the Gauss pseudospectral method based optimal guidance control has a lower fuel consumption and higher accuracy， so the latter is feasible for engineering practice.

small body; optimal attaching guidance; phase plane method; Gauss pseudospectral method

2014-12-26

2015-02-20

国家自然科学基金资助项目(61273051， 60804057)；国家高技术研究发展计划(863计划)项目(2011AA7034057E，2012AA121601)；上海航天科技创新基金项目(SAST201213)

V448.12

A

2095-7777(2015)01-0053-08

10.15982/j.issn.2095-7777.2015.01.008