基于燃料最优解的火星精确着陆制导策略研究

郭延宁，马广富，曾添一，崔祜涛

(1.哈尔滨工业大学 控制科学与工程系， 哈尔滨 150001；2.哈尔滨工业大学 深空探测基础研究中心， 哈尔滨 150001)

基于燃料最优解的火星精确着陆制导策略研究

郭延宁1，马广富1，曾添一1，崔祜涛2

(1.哈尔滨工业大学 控制科学与工程系， 哈尔滨 150001；2.哈尔滨工业大学 深空探测基础研究中心， 哈尔滨 150001)

针对火星着陆任务高实时性和低燃耗的需求，提出了一种新的基于开环燃料最优解的精确着陆制导策略。通过分析开环燃料最优解特性，设计了利用发动机推力幅值切换处的状态作为路径点结合最优线性制导律进行分段制导的制导策略，在无需存储全部燃料最优轨迹的前提下，实现具有近燃料最优特性的着陆任务，节省了大量的存储空间。同时详细讨论了包括全局燃料最优解获取、路径点提取、路径点拟合等一系列关键问题，并通过典型火星着陆场景的大量数学仿真验证了所提出策略的可行性和优越性。

精确着陆；动力下降；路径点；最优制导；轨迹跟踪

0 引 言

深空探测及行星着陆采样等关键技术为人类研究宇宙起源、开发和利用空间资源奠定了基础。特别是地球的近邻火星，成为人类向外太空开拓的首选。美国“好奇号”火星车于2011年成功着陆，掀起了新一轮行星探测及着陆任务热潮。印度和美国分别于2013年11月5日和18日发射了“火星轨道探测器”和“火星大气与挥发演化任务”探测器，各自已经于2014年9月24日和22日成功进入火星轨道，将为研究火星气候与环境的演变带来新的机遇。此外，美国的火星样本取回计划：预计于2016年将500 g火星土壤带回地球。我国“嫦娥3号”的软着陆和月球车投放任务的成功实施，实现了动力下降、月面生存与深空测控通信等一系列关键技术的突破，未来的火星探测及着陆任务也进入最后的准备阶段。

在包括火星在内的所有行星着陆的最后阶段，均需利用反推力发动机进行有效减速并实现目标点安全精确着陆，该阶段即动力下降段。由于不同行星大气层的成分及厚度等信息存在差异，对应动力下降段的时间跨度各不相同。动力下降段面临精度需求高、复杂地形多、环境不确定性强以及时间短等诸多挑战，因此其导航、制导与控制系统的性能将直接决定整个着陆任务的成败，是火星探测任务需要攻克的最关键技术之一[1-2]。

动力下降段制导与控制系统的目的是在满足控制约束、障碍回避及燃料约束的前提下，通过设计加速度或推力指令，利用推力发动机产生推力，实现预定着陆点或其附近区域安全着陆。已有的制导系统设计可大致分为显式制导律、轨迹优化以及轨迹跟踪制导律三种。

显式制导律中最经典的方法为阿波罗任务月球着陆器采用的二次多项式制导方案，此外还包括D’Souza等(1997)[3]总结提出的最优制导律、Steinfeldt等(2010)[4]改进的基于自调节飞行时间的最优制导律、Najson等(2006)[5]提出的燃料高效末端制导律、Furfaro等(2011)提出的基于非线性滑模的精确着陆制导律[6]以及基于强化学习方法的燃料高效精确着陆制导策略[7]、Guo等(2013)[8]提出的通用的基于零控位置误差/零控速度误差(ZEM/ZEV)的最优制导律等，此外针对行星表面障碍物的探测和规避问题也有一定研究进展[9]。显式制导律具有实时性好、鲁棒性高等优点，但是在燃耗性能、障碍回避能力等方面表现不佳，不适合未来发展需求。

获取燃料最优解是所有消耗燃料的航天器需要面对的问题，而该问题对于深空探测任务尤为重要。由于着陆过程一般采用可变推力发动机，着陆任务完成前需保持点火状态，因此存在最大和最小推力约束。目前已有的研究方法包括基于凸优化方法的燃料最优火星精确着陆轨迹优化[10]、基于凸优化的燃料有限情况下火星着陆区优化[11]、基于勒让德伪谱法的火星燃料最优轨迹优化[12]、基于降敏感度最优控制的燃料最优化分析[13]、以及粒子群算法[14]、θ-D方法[15]等。随着优化理论的发展和计算机计算能力的提升，基于在线轨迹优化的制导系统将成为未来任务首选，但当前的探测器尚不足以完成全自主在线优化计算。

为使得探测器实现燃料最优或近最优精确着陆，可行的方案为通过载入离线优化得到的最优轨迹作为参考轨迹，设计轨迹跟踪制导策略，在存在导航误差、模型不确定性和未知干扰的情况下，确保实际飞行轨迹与参考轨迹一致，已有的轨迹跟踪制导方案见文献[16]～文献[18]。但是对于参考轨迹的特征提取以及存储方式目前研究较少，存储所有可能的最优轨迹对于探测器的存储量和计算量需求过高，且依赖开环优化轨迹并不能根据当前状态调整，所以该制导策略存在性能退化甚至障碍碰撞危险。

针对以上问题，Guo等(2013)[19]提出了利用一个优化所得的路径点结合最优显式制导律实现近燃料最优火星精确着陆的新思路，仅通过存储离线优化得到的一个路径点而非整条轨迹，利用实时性较好的最优制导律依次使得探测器飞行到路径点和期望着陆区。不过该方法依赖第三方优化软件性能，不能确保路径点的有效性，且在处理各种约束情况时不够灵活。

综上，本文将继续研究基于燃料最优解的火星精确着陆制导方案，在分析归纳基于轨迹优化解的制导方法和燃料最优轨迹特性的基础上，提出一种新的路径点选取方法，最后针对典型火星着陆场景进行数学仿真验证，对本文提出的方案的有效性和实用性开展深入分析。

1 动力下降段问题描述

考虑火星着陆器在动力下降段已经接近火星表面且速度相对较低，忽略火星大气气动阻力的影响以及火星的自转，火星着陆器在动力下降段的运动方程可表示为

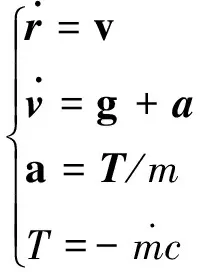
(1)

其中：r，v分别表示探测器相对期望着陆点的位置和速度矢量；a为推力发动机产生的控制加速度矢量，对应推力矢量和推力幅值分别为T和T；g为火星的重力加速度矢量；m为着陆器质量；c为推力发动机质量排出速度。

2 燃料最优轨迹优化问题及求解

2.1 问题描述

对于给定探测器初始时刻和最终时刻tf状态

(2)

其中：r0为探测器初始位置；v0为探测器初始速度；m0为探测器初始质量。

考虑发动机存在最大T2和最小T1的推力约束

(3)

以及着陆过程下降倾角θ约束

(4)

其中ri(i=h，x，y)代表探测器位置矢量在垂直以及水平面内两个正交方向的分量。

最小化如下性能指标

(5)

对应的最优解r*即为燃料最优着陆轨迹。

2.2 问题求解

轨迹优化将连续系统的最优控制转换为离散系统的非线性规划问题。对于一般的轨迹优化问题，常用的方法有间接法和直接法。前者需要结合系统动力学或结构特性进行求解，而后者则通过参数化方法转换得到等价的数值优化问题，特别是随着非线性优化和计算机速度的发展，各种商用及免费的优化软件不断涌现，为该问题的求解带来便利。

对于2.1节描述的轨迹优化问题，针对式(3)所示的非凸约束，可以参考文献[10]先将其等价转换为凸约束的二阶锥优化(SOCP)问题求解，也可以直接利用优秀的商业优化软件TOMLAB等计算，均可得到一致的燃料最优轨迹及控制力矢量等。不过，在飞行时间未给定的情况下，为了获得全局最优解，文献[10]采用了线性搜索法，计算时间较长。

大量数值计算研究发现，不同飞行时间对应的最小燃耗具有凸函数性质，因此可借鉴二分法思想，采用如下三分法获得全局最优解。

1)利用二分法确定最小可行飞行时间tl，结合任务需求及经验给定区间[tl，tu]，求解端点时刻燃料最优化问题，获得优燃耗ml和mu。

2)将该区间三等分，即t1=tl+(tu-tl)/3，t2=tu-(tu-tl)/3，获得对应最优燃耗m1和m2。

3)若m1>m2则取[t1，tu]为新的区间，否则取[tl，t2]。

4)重复步骤2和3，直到满足系统精度需要。

3 基于燃料最优解的制导方案设计

3.1 轨迹跟踪策略

无论存储完整燃料最优轨迹还是路径点，探测器都不可能遍历所有可能的情况。如果实际着陆时初始状态不能和未能直接匹配，需要通过函数拟合或插值的方法获得任意初始状态对应的最优轨迹。

因此，可设计轨迹跟踪制导策略来跟踪燃料最优轨迹，主要步骤为：

1)将探测器可能的初始状态分割成均匀的网格，针对网格状态优化得到最优轨迹和最优控制；

2)对最优轨迹进行分段、编码，生成轨迹库，存储到探测器中；

3)探测器在动力下降段开始时刻，查询轨迹库中与当前状态最接近的一组或几组状态拟合得到参考最优轨迹和参考最优控制；

4)设计基于标称模型的轨迹跟踪制导律来跟踪最优轨迹。

此外，由于动力下降段的起点为探测器推力发动机点火，其初始质量可视为已知量，而初始位置、初始速度等则需要进行大量的计算和分析。

直接基于最优控制加速度和状态的跟踪制导律可设计如下

(6)

其中：a*(t)、 r*(t)和v*(t)分别为利用轨迹库中的离散点和当前时刻插值得到的当前时刻的最优控制加速度、位置矢量和速度矢量；Kr和Kv为待选取的增益矩阵。

然而该方法需要给探测器注入大量的轨迹，很难满足着陆任务的实时性、可靠性、鲁棒性等需求。

3.2 基于燃料最优解的路径点获取

虽然文献[19]已经提出基于路径点的着陆制导策略，并充分说明了该方案的优越性，但路径点的获取需要编写单独的优化程序，且目前尚不能够有效处理如最小推力幅值等约束。

由燃料最优化问题的特性可知，其最优控制仅工作在极值状态，对应本文研究的精确着陆问题，即推力发动机幅值始终处于上限或下限。针对某典型情况的推力程度统计结果如图1所示(对应着陆轨迹详见仿真分析部分图7)。

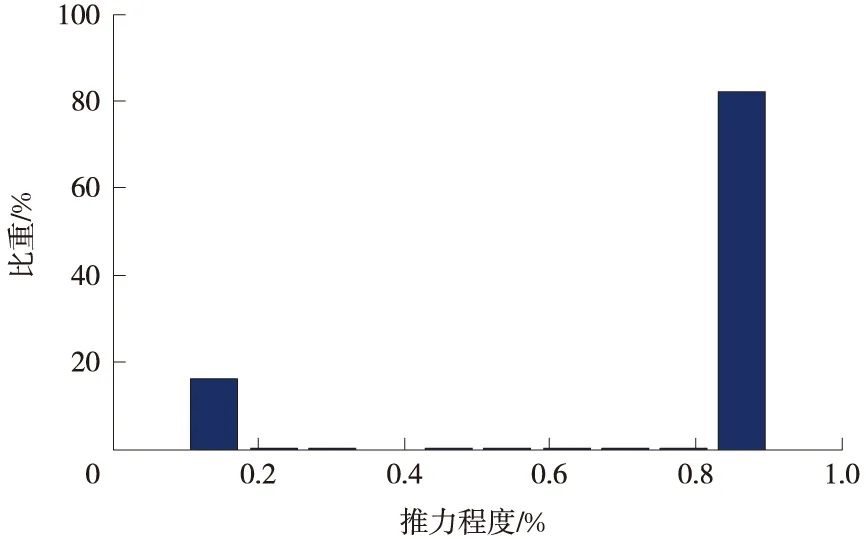
图1 典型燃料最优解对应推力幅值分布情况Fig.1 Typical thruster force distribution of fuel optimal solution

大量仿真计算表明，推力幅值曲线可分为“最大-最小-最大”和“最小-最大”两种情况。因此，若能将燃料最优解中推力切换处的状态设置为路径点，分别定义为(tw1，rw1，vw1)和(tw2，rw2，vw2)，利用具有线性特性的制导律实现分段控制，则可能使得探测器沿着燃料最优轨迹飞行，进而具备近燃料最优的特性。

路径点策略在实际应用时同样面临不能遍历的情况，最简单的方式是采用距离最近的网格对应的路径点作为指令状态，但该情况需要网格足够精细，否则可能带来着陆性能的显著下降甚至失败。另一种可行的方法为利用k个距离最近的网格拟合，设探测器初始状态可表示为

(7)

其中：mi和ni为权重系数；r0{i}和v0{i}代表第i组网格对应的初值。

加权后即可获得指令路径点时间和状态如下

(8)

(9)

其中加权常数λ需要基于最优数据根据经验选取。

3.3 线性反馈制导律

路径点选取后，还需要设计具有线性特性的制导律，设线性制导律形式的控制加速度为

(10)

其中m，n为待定常矢量，则有t时刻探测器速度矢量为

(11)

其中t0为初始时刻。

进一步地，有t时刻探测器位置矢量为

(12)

特别地，对于给定期望末端时刻tf和末端状态vf，rf，并定义tgo=tf-t0，有

(13)

(14)

联立方程和方程，可得

(15)

将式代入方程，可得在当前时刻的控制加速度为

a(t)=t0m+n-g=

(16)

考虑控制推力幅值上限情况时，可对控制加速度的幅值进行约束

(17)

其中Tmax为推力幅值上限，饱和函数的定义为

(18)

其中|q|表示矢量q的元素的最大绝对值。

特别地，定义零控位置误差(zero-effort-miss，ZEM) 和零控速度偏差(zero-effort-velocity，ZEV)为不加入控制推力情况下tf时刻探测器位置和速度与期望位置和速度偏差，如下

(19)

则制导律可表示为

(20)

4 典型数值仿真验证及结果分析

本节以某火星探测器为背景，来验证所提出的“路径点+线性制导”策略的有效性。该探测器及进行轨迹优化相关的参数如表1所示。

表1 火星探测器参数

4.1 某典型初值情况

设探测器在到达2 000 m高度时切换到动力下降阶段，取初值r0和v0分别为[2 000，0，-8 000]m和 [-75，0，100]m/s，参考文献[10]将燃料最优化问题转换为SOCP问题，并利用SDPT3软件求解，利用三分法搜索可得最优下降时间tf*为69.8s，进而可得燃料最优解对应的位置、速度、控制加速度、推力幅值以及着陆器质量变化曲线如图2～图6(标记为FuelOpt的曲线)所示。

图5所示的推力幅值曲线呈现“最大-最小-最大”的结构，且三个阶段对应图4的各轴控制加速度曲线近似为线性，因此可提取两次切换状态作为两个路径点，路径点一位于25.1s，对应位置和速度分别为[997.0， 0.0，-471 6.7]m和[0.45，0.00，147.27]m/s，路径点二位于42.5s，对应位置和速度分别为[555.8，0.0，-2 168.0]m和[-50.40，0.00，144.03]m/s。

利用3.3节给出的最优线性反馈制导律(17)驱动探测器依次飞行到两个路径点及最终着陆区，对应的仿真结果如图2～图6(标记为Waypoint曲线)所示。可以看出，利用本文所提出策略对应的位置、速度曲线几乎与燃料最优结果完全重合，充分验证了采用线性制导律进行分段制导的可行性；图4所示的两种策略的控制加速度曲线在路径点切换时存在显著区别，主要是在到达制导目标前tgo出现极小值造成的，基本不会影响着陆性能。虽然线性制导律对应图5所示的推力幅值曲线与燃料最优情况存在一定差别，但始终未超出推力发动机最大幅值，对应的燃耗情况也极为接近。需要注意的是，由于两种策略考虑的最大推力幅值并不相同，所以不宜简单通过燃耗评价优越性。

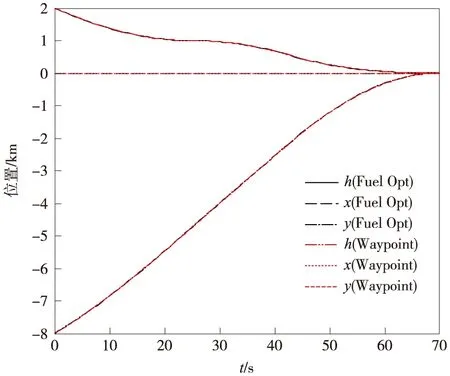
图2 不同策略对应位置曲线Fig.2 Time histories of position using different strategies

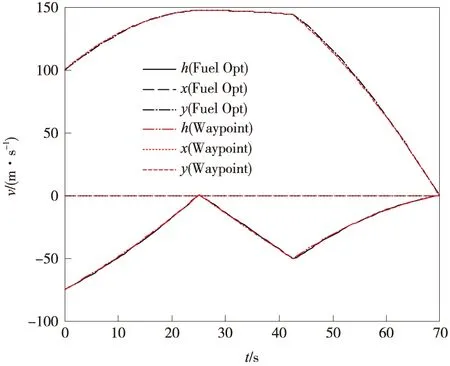
图3 不同策略对应速度曲线Fig.3 Time histories of velocity using different strategies

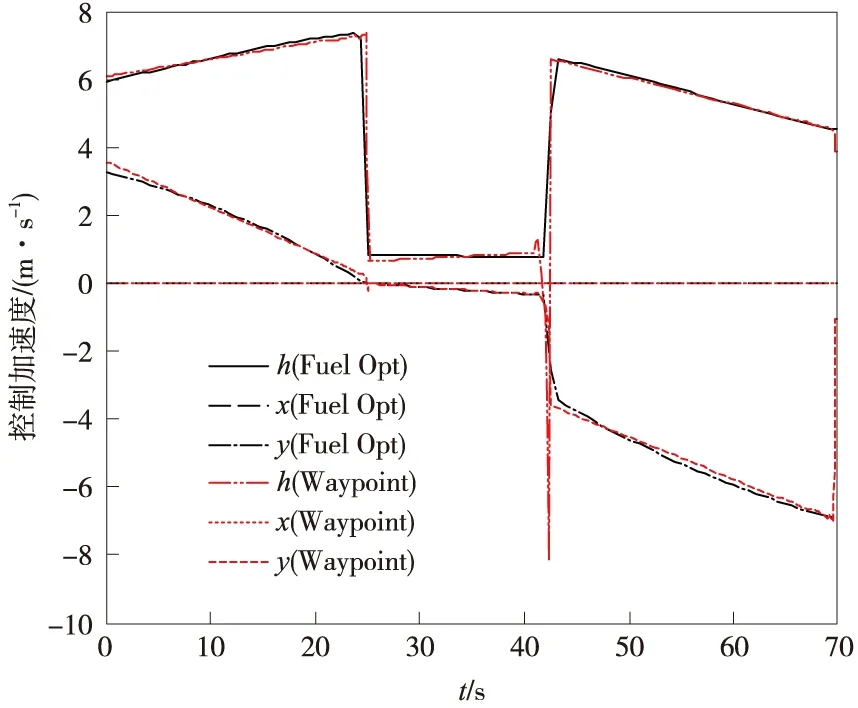
图4 不同策略对应控制加速度曲线Fig.4 Time histories of control acceleration using different strategies

图5 不同策略对应推力幅值曲线Fig.5 Time histories of control force magnitude using different strategies

图6 不同策略对应着陆器质量曲线Fig.6 Time histories of spacecraft mass using different strategies

4.2 多种初值情况

为充分验证本文提出方案的实用价值，继续采用表1中的探测器参数和4.1节中的初始速度，保持初始高度为2 000 m，初始位置水平方向从-8 000到3 000 m改变，可得开环燃料最优和本文提出制导策略对应的下降轨迹簇如图7所示，图7还分别给出了每种情况对应的两个路径点位置分布情况，其中初始水平位置为-2 000 m时对应推力幅值为“最小-最大”形式，因此设定路径点一为起点。

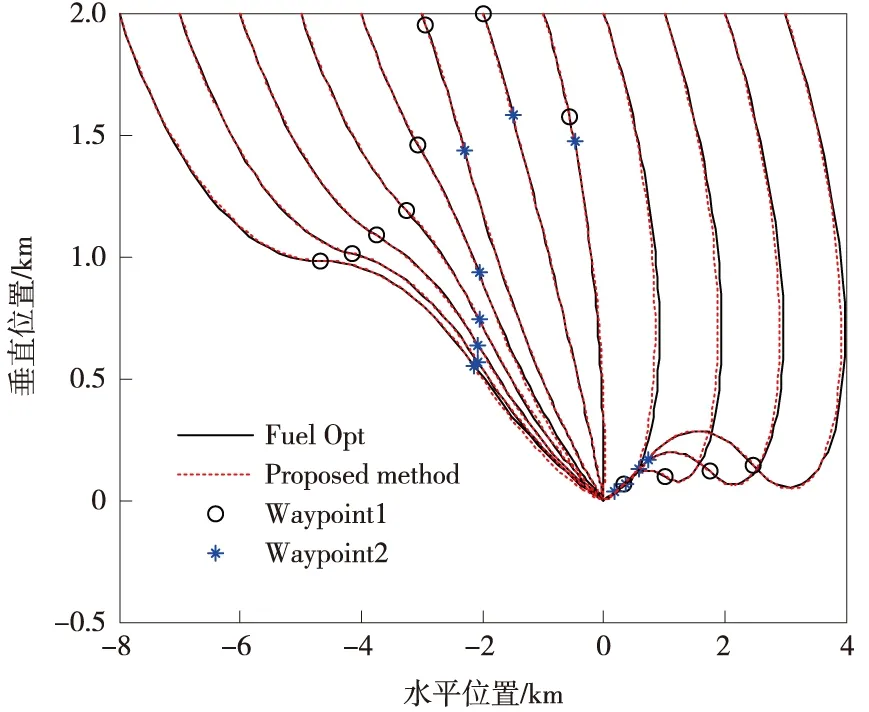
图7 不同起点情况下本文算法与燃料最优着陆轨迹对比Fig.7 Landing trajectory comparisons of the proposed method with fuel optimal results for various initial conditions

由轨迹对比情况可以看出，本文提出“路径点+线性制导”策略完全可以达到“最优轨迹+轨迹跟踪”制导策略的性能，而且对于数据存储的需求极低，且该线性制导律的高度通道可以加入障碍回避项，使其具有更高的自主性和可靠性。

4.3 一组路径点用于多组初值情况

考虑探测器实际着陆时初始速度与最优轨迹对应一致，但高度和水平位置分别在2 000～2 500 m和1 500～2 500 m取值时，直接应用[2 000，0，2 000] m对应的两个路径点与线性制导律结合，可得着陆轨迹簇和不同初值对应的燃耗情况如图8～图9所示。

图8 不同初始位置对应的着陆轨迹Fig.8 Trajectories correspond to various initial positions

图9 不同初始位置对应的燃耗Fig.9 Fuel usages correspond to various initial positions

可以看出，对于该初始情况，由于路径点一处于飞行过程后段，因此线性制导律有较多的自由度和时间实现状态转移，确保了路径点二和最终着陆区的着陆精度。此外，由图9可以看出，虽然探测器初始位置在较大范围内变化，但对应的燃料消耗却大致在390～410 kg区间内变化，上下幅度小于2.5%，一定程度上说明了单组路径点的使用范围。

4.4 路径点线性拟合情况

虽然上节的测试说明路径点允许初始情况在一定范围变化，但主要还是对于处于“最小”推力的时间较长的情况，比如图7中水平位置初始为-1 000 m情况，推力发动机绝大多数工作在最大推力状态，就会对于初值非常敏感。

本节测试采用线性拟合的方式获得路径点的性能。基于图7给出的燃料最优轨迹路径点，保持探测器初始高度不变，初始水平位置在-8 000～3 000 m内连续取值，利用线性插值可得两个路径点，对应采用线性制导律得到的探测器着陆轨迹和燃耗性能曲线如图10～图11所示。

图10 线性插值拟合获取路径点对应的着陆轨迹Fig.10 Trajectories correspond to waypoints obtained through linear interpolation

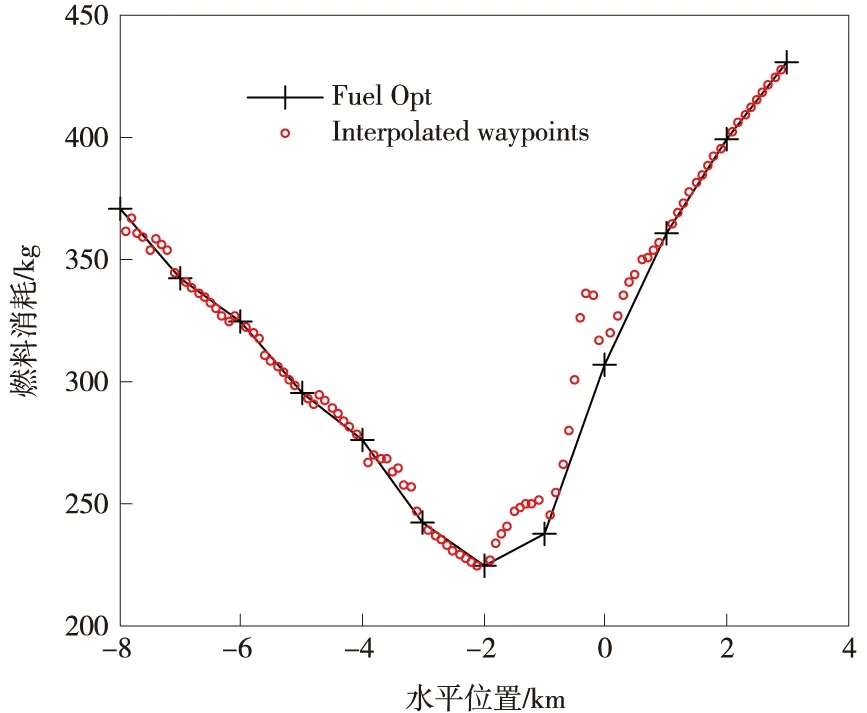
图11 线性插值拟合获取路径点的燃耗性能Fig.11 Fuel usage performance using waypoints obtained through linear interpolation

图10中的实线和虚线分别代表燃料最优轨迹和“拟合路径点+线性制导”策略对应轨迹，可以看出后者出色地完成了精确着陆任务，且对应轨迹基本位于最近的两条燃料最优轨迹中间，说明了路径点拟合方法的重要应用价值。图11所给出的燃耗性能对比说明了通过拟合路径点可以以近燃料最优的性能完成着陆任务。

5 结 论

由于火星着陆燃料最优解对应的控制力呈现分段连续状态，且每一段大致为线性，本文通过设定最优控制切换时刻对应状态为路径点，并利用线性制导律进行分段制导，构造了一种新的“路径点+线性制导律”的制导策略。该策略不仅具备显式制导的强实时性和高可靠性特性，还可以使得探测器基本沿燃料最优轨迹飞行，进而具备近燃料最优特性，且不需要存储全部飞行轨迹。典型火星着陆场景验证了该方案的优越性，也分析了路径点线性拟合策略的可行性，充分表明了其工程应用价值。

值得提出的是，本文的数值仿真算例仅给出了几种典型的火星着陆任务，且仅考虑了初始位置的变化，后续工作尚需要进一步完善和测试路径点拟合机制，同时在线性制导律中加入自主障碍回避等功能。

[1] Braun R D， Manning R M. Mars exploration entry， descent and landing challenges[J]. Journal of Spacecraft and Rockets， 2007，44(2):310-323．

[2] 安德鲁·鲍尔等著. 行星着陆器和进入探测器[M].殷前根等译.北京:中国宇航出版社，2010.[ Ball A J，et al. Planetary landers and entry probes[M]. Translator， Yin Q G， et al. Beijing: China Astronautic Publishing House， 2010.]

[3] D’Souza C N. An optimal guidance law for planetary landing[C]∥Proceedings of the AIAA Guidance， Navigation and Control Conference. New Orleans:[s.n.]， 1997．

[4] Steinfeldt B A， Grant M J， Matz D A，et al. Guidance， navigation， and control system performance trades for Mars pinpoint landing[J]. Journal of Spacecraft and Rockets， 2010，47(1):188-198．

[5] Najson F， Mease K D. Computationally inexpensive guidance algorithm for fuel-efficient terminal descent[J]. Journal of Guidance， Control， and Dynamics， 2006，29(4):955-964．

[6] Furfaro R， Selnick S， Cupples M L， et al. Non-linear sliding guidance algorithms for precision Lunar landing[C]∥21st AAS/AIAA Space Flight Mechanics Meeting. Louisiana， New Orleans:[s.n.]， 2011：945-964．

[7] Gaudet B， Furfaro R. Adaptive pinpoint and fuel efficient Mars landing using reinforcement learning[C]∥22ed AAS/AIAA Space Flight Mechanics Meeting. Charleston， South Carolina:[s.n.]， 2012:1309-1328．

[8] Guo Y， Hawkins M， Wie B. Applications of generalized zero-effort-miss / zero-effort-velocity feedback guidance algorithm[J]. Journal of Guidance， Control and Dynamics， 2013，36(3):810-820．

[9] Rutishauser D K， Epp C D， Robertson E A. Free-flight terrestrial rocket lander demonstration for NASA’s autonomous landing and Hazard avoidance technology (ALHAT) system[C]∥AIAA SPACE 2012 Conference & Exposition. Pasadena， California:[s.n.]， 2012．

[10] Acikmese B， Ploen S R. Convex programming approach to powered descent guidance for Mars landing[J]. Journal of Guidance， Control， and Dynamics， 2007，30(5):1353-1366.

[11] Acikmese B， Blackmore L. Lossless convexification of a class of optimal control problems with non-convex control constraints[J]. Automatica， 2011，47(2):341-347．

[12] Sostaric R R， Rea J R. Powered descent guidance methods for the Moon and Mars[C]∥AIAA Guidance， Navigation， and Control Conference and Exhibit. San Francisco， California:[s.n.]， 2005．

[13] Shen H J， Seywald H， Powell R W. Desensitizing the minimum-fuel powered descent for Mars pinpoint landing[J]. Journal of Guidance， Control， and Dynamics， 2010，33(1):108-115．

[14] Brian Kent Birge III. A computational intelligence approach to the Mars precision landing problem[D]. PhD dissertation of North Carolina State University， 2008.

[15] Liu R， Li S， Chen X， et al. Powered-descent trajectory optimization scheme for Marslanding[J]. Advances in Space Research, 2013， 52(11):1888-1901．

[16] Singh G， SanMartin A M， Wong E C. Guidance and control design for powered descent and landing on Mars[C]∥IEEE Aerospace Conference. [S.l.]: IEEE， 2007:1-8．

[17] Cui P Y， Gao A， Cui H T. Receding Horizon-based dual control strategy for pinpoint planetary landing[J]. Transactions of the Japan Society for Aeronautical and Space Sciences， 2012，55(4):222-228.

[18] Li M D， Jing W X， Macdonald M，et al. Adaptive backstepping control for optimal descent with embedded autonomy[J]. Aerospace Science and Technology， 2011，15(7):589-594．

[19] Guo Y， Hawkins M， and Wie B. Waypoint-optimized zero-effort-miss / zero-effort-velocity feedback guidance for Mars landing[J]. Journal of Guidance， Control， and Dynamics， 2013，36(3):799-809． 作者简介： 郭延宁(1985—)，男，讲师，硕士生导师，主要研究方向：行星着陆器制导与控制、航天器姿态动力学与控制。 通信地址：哈尔滨市西大直街92号哈尔滨工业大学327信箱主楼606室(150001) E-mail:guoyn@hit.edu.cn

[责任编辑：高莎]

Mars Precision Landing Guidance Strategy based on Fuel Optimal Solutions

GUO Yanning1， MA Guangfu1， ZENG Tianyi1， CUI Hutao2

(1.Department of Control Science and Engineering， Harbin Institute of Technology， Harbin 150001， China;2.Deep Space Exploration Research Center， Harbin Institute of Technology， Harbin 150001，China )

In order to satisfy real time and low fuel consumption requirements of Mars descent phrase， a new Mars precision landing guidance strategy was proposed based on fuel optimal solutions. Based on the characteristic analysis of the open loop fuel optimal solutions， states corresponding to thruster force magnitude switching time are directly selected as intermediate waypoints， and then a linear guidance algorithm was implemented in each segments to achieve fuel optimal performance. Several key problems， including the computation of global fuel optimal solution， waypoint selection， waypoint fitting， and derivation of linear guidance algorithm， were discussed in details， and the feasibility and superiority of the proposed strategy have been evaluated through a variety of typical Mars landing scenarios．

precision landing； dynamic descent； waypoint； optimal guidance； trajectory tracking

2014-12-01

2015-02-12

国家973计划项目(2012CB720000) ；国家自然科学基金资助项目(61403103)；中国博士后科学基金资助项目(2014M550195)

V249.122.5

A

2095-7777(2015)01-0061-08

10.15982/j.issn.2095-7777.2015.01.009