基于三维空间信道的同心圆天线阵列模型研究

陈中良，潘 浩

(1. 黄淮学院，河南 驻马店 463000；2. 武汉大学 计算机学院，湖北 武汉 430072)

基于三维空间信道的同心圆天线阵列模型研究

陈中良1，潘 浩2

(1. 黄淮学院，河南 驻马店 463000；2. 武汉大学 计算机学院，湖北 武汉 430072)

提出了三维(Three Dimension，3D)信道模型下的新型的同心圆天线阵列模型，数值推导该模型的空间相关性与扩展方位角(Azimuth Spread，AS)和俯仰角(Elevation Spread，ES)，平均中心到达方位角(Mean Azimuth of Arrival，MAOA)和俯仰角(Mean Elevation of Arrival，MEOA)的函数关系式，通过MATLAB数值仿真，比较不同阵元位置以及不同的空间到达角度对于线性(Uniform Liner Array，ULA)阵列，圆形(Uniform Circular Array，UCA)阵列以及提出的新型同心圆天线阵列结构的空间相关性分布情况，从而验证提出的天线阵列结构具有优越的高容量的性能，进而推动无线通信领域的研究与发展。

同心圆天线阵列；线性阵列；圆型阵列；空间相关性

1 天线阵列

在无线通信环境中，电磁信号从发射端到接收端的过程中往往会经历复杂的传播环境，这也使得接收信号存在不同程度以及不同类型的衰落，从而影响了通信质量。多输入多输出(Multiple Input Multiple Output，MIMO)作为现代以及未来移动通信关键技术之一，已经逐渐体现出其能够提高信道容量以及频谱利用率的强大优势。MIMO系统作为一项运用于IEEE802.11n的核心技术[1]，能够接收丰富的信号多径分量，有效地抑制信号深度衰落。研究表明MIMO系统的容量取决于信道矩阵的秩，而信道矩阵的秩则依赖于天线信号衰落的相关性，所以天线阵元间相关性是决定信道容量的关键因素。

在过去关于MIMO多天线系统性能的探索中，文献[2]分析了信道相关性对于空间信道性能的影响，研究了调节信道参数以提高系统性能；文献[3]建立了椭圆MIMO信道模型，综合考虑了收发端附近存在有散射体，分析了空间相关性系数与发射端、接收端天线间距，角度扩展以及扩展因子之间的关系。文献[4]提出了两类MIMO信道，一类是适合室外通信环境的圆环模型(One-ring Model)，另一类则是适合室内通信环境的椭圆模型(Elliptical Model)，并且通过数值仿真，结果分析了到达角度(Angle of Arrival，AOA)对于空间相关性的影响，进而探究了多天线系统的性能。文献[5-6]数值推导出入射信号的角能量分布在均匀分布(Uniform)以及拉普拉斯分布(Laplacian)下的线性阵列(Uniform Liner Array，ULA)以及圆形阵列(Uniform Circular Array，UCA)天线阵元间的空间相关性函数(见图1、图2)。以上关于空间信道天线阵列的研究大都局限于二维平面上，而忽视了入射信号竖直平面上的夹角对于系统性能的影响。文献[7]针对传统三维单环MIMO信道模型的不足进行改进，建立了三维环境下适用于任意极化分集的统计随机MIMO信道模型，推导出的这个近似表达式能够很好地表达空间特性。后来，文献[8-9]对三维空间信道的线性以及圆形的天线阵列结构进行分析研究，考虑扩展方位角(Azimuth Spread，AS)和俯仰角(Elevation Spread，ES)，平均中心到达方位角(Mean Azimuth of Arrival，MAOA)和俯仰角(Mean Elevation of Arrival，MEOA)对于三维天线阵列相关性的影响。为了满足用户对信道的高容量需求，文献[10]提出了一种新型的圆环天线阵列结构，数值推导该阵列下的空间相关性函数，并且分析了不同阵元环境下的相关性分布情况，然而Lee并没有表明同心圆天线阵列与ULA以及UCA阵列的优越性，同时也没有对同心圆天线阵列的信道容量进行分析，本文的研究是弥补该领域的空白，从而进一步推动三维空间信道的同心圆天线阵列模型的研究。

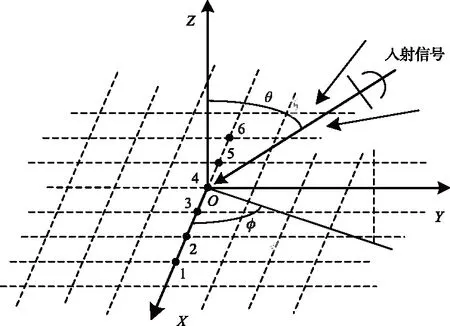
图1 线性天线阵列结构

图2 圆形天线阵列结构

多天线阵列能够有效利用空间信道中的多径分量，具有极高的频谱利用率，文献[5-8]指出，在发射端设置线性以及圆形天线阵列，并且利用此信道的多径分量特征在不增加带宽的情况下提高通信系统的容量，具有极大的现实意义。过去关于多天线阵列结构的研究大多集中在线性以及圆形阵列，其中线性天线阵列结构比较简单，而圆形天线阵列全方向性比较强，这也就使得在无线移动通信环境中得到广泛应用。文献[2]表明，对于过去的线性以及圆形阵列，当空间信道的相关性增大到一定程度，多天线系统将不再适用。鉴于获得较为丰富的多径分量，本文提出了一种新型的同心圆天线阵列结构，数值推导出不同阵元在三维空间中的相关性函数，并且通过MATLAB数值仿真，研究比较不同的阵元位置以及不同的空间角度对于线性ULA、圆形UCA以及新型同心圆天线阵列结构的空间相关性影响，从而验证本文提出的阵列结构的优越性，进一步推动无线通信领域中关于天线阵列研究的发展。

2 三维多天线阵列结构模型

[5-7]表明，在发射端和接收端设置有多输入多输出MIMO系统能够有效地提高信道的容量，然而入射信号未知的空间角度参数会直接影响阵列天线的阵元间信道相关性，进而影响多天线系统的性能，因此研究多天线系统的空间相关性也就具有一定的现实意义。

2.1 线性以及圆形多天线阵列

在三维移动通信传播环境中，假设入射信号在水平面上的夹角为φ，取值范围是0≤φ≤2π；而在竖直方向上的夹角为θ，取值范围是0≤θ≤π/2。过去关于多天线阵列结构的研究大多集中在线性以及圆形阵列，其中线性天线阵列结构比较简单(详见图1)，而圆形天线阵列全方向性比较强(详见图2)，这也就使得在无线移动通信环境中得到广泛应用。其中入射信号在三维线性阵列的空间导向矢量可以表示为

(1)

式中：M为接收端的天线数目；d为天线两阵元之间的距离；λ则是入射信号的波长；[·]T表示矩阵的转置。而对于半径为r的圆形UCA阵列，其导向矢量可以表示为

(2)

结合以上分析，伴随无线通信的不断深入研究，线性ULA以及圆形UCA已经逐渐不能满足用户对于信道高容量的要求。因此本文关于新型的同心圆天线阵列的研究也就存在一定的现实意义。

2.2 新型圆环多天线阵列

在图3所示的三维移动通信环境下的新型的同心圆天线阵列结构中，选取阵列中的任意两环(内环和外环)作为研究对象，假设内环外环均有4个阵元，并且内环和外环中的阵元到坐标原点的距离分别表示为Rm和Rn。通过数值推导，求出阵元m和n之间在散射体均匀分布下的空间衰落相关函数[9]为

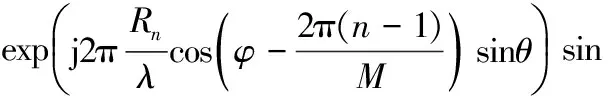
(3)

图3 新型同心圆天线阵列结构

参考文献[7]证实了影响多输入多输出系统性能的主要因素是入射角的角度扩展(AOA和EOA)，在本文以上信道相关时函数关系式的推导中假设入射角的概率密度为均匀能量分布，其中平均中心到达方位角以及水平扩展角分别表示为φ0和Δφ；而平均中心到达俯仰角以及竖直扩展角分别表示为θ0和Δθ。通过数值计算，可以将式(3)进一步推导为

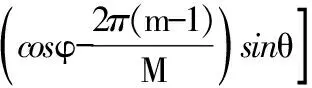
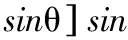
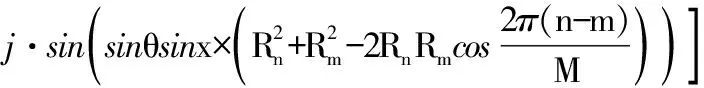
sinθdxdφ

(4)

以上研究并推导了入射信号的角能量均匀分布在同心圆天线阵列的空间相关性函数，研究了空间相关性与阵元间距、扩展方位角和俯仰角、平均中心到达方位角和俯仰角的函数关系式。

3 多天线系统容量

在三维移动通信系统中，信道容量能够比较全面地描述多输入多输出系统的性能。参考文献[8]表明，多天线阵列信道容量可以近似表示为

(5)

式中：IM是M维的单位矩阵，而N以及M分别是发射端和接收端天线的数量；Rt和Rr分别是发射端和接收端的阵元之间的相关性系数；P/σ2是信道的误码率，而复高斯随机矩阵可以表示为Hw。

4 仿真结论与分析

过去研究表明，线性ULA阵列结构简单，操作性强；而圆形UCA阵列全方向性较好，在移动通信领域应用的较多。为了确保以下的仿真结果符合客观实际，采取内环中的阵元m到坐标原点的距离Rm=10 m，外环中的阵元n到坐标原点的距离Rn=20 m,30 m。除此之外，水平方位扩展角AS=30°,60°以及ES=30°,60°，而平均中心到达角MAOA=30°,60°以及MEOA=30°,60°。

4.1 多天线相关性分析

图4是阵元间距对ULA、UCA以及UCRA阵列空间相关性的影响，数值仿真结果显示空间相关性ρ随着阵元间距的增大而逐渐减小，并且在d从0～λ的过程中相关性系数降低的比较快，而在d>λ之后则是以小幅度振荡逐渐递减。从图中还可以发现，当Rn/Rm的比值增大，即内环与外环的间距逐渐增大时，阵元之间的影响作用较低，相关性系数降低。除此之外，与线性ULA及圆形天线UCA阵列相比，同心圆天线阵列可以呈现一个较为理想的相关性，即相关性系数较低，这也在某种层面上反映出本文提出的同心圆天线阵列具有较为理想的应用前景，具有一定的研究意义。图4的仿真结果与文献[7]的研究结果相符合，表明此结果适用于描述三维空间信道的接收阵列模型。

图4 阵元间距对ULA、UCA以及UCRA阵列空间相关性的影响

图5所示为电磁信号的水平以及竖直扩展角AS和ES对线性ULA、圆形UCA以及本文提出的天线阵列结构的空间相关性的影响，从图中可以发现，俯仰角ES对于空间相关性的影响较小，并且相关性系数关于ES=90°左右对称；与此同时，根据相关性曲面在x轴上的投影可以看出，线性、圆形以及本文提出的圆环天线阵列的相关性趋势相似关于AS=90°对称。除此之外，从图中还可以发现，线性和圆形的相关性系数都保持在0.8以上，表明阵元之间的相关性较强，这样在很大程度上影响电磁信号的发送和接收；而本文提出的同心圆天线阵列结构的空间相关性系数则是相对较小，并且当内环以及外环的间距变大时，阵元1和5之间的相关性较小。以上的仿真结果与文献[7]的研究相符合，表明此结果与客观实际相吻合。

图5 扩展角AS和ES对于空间相关性的影响

图6示电磁信号的平均中心到达角MAOA和MEOA对本文提出的天线阵列结构的空间相关性的影响，其中方位扩展角φ和俯仰扩展角θ固定为30°。从图中还可以发现，本文提出的同心圆天线阵列中的任意两个阵元的相关性受MAOA的影响较小，而随着MEOA的增大呈缓慢衰落的趋势。除此之外，当内环以及外环的间距变大时，阵元1和6之间的相关性程度与阵元1和5之间的相关性程度较小，这是因为阵元1和6之间的间距较大。

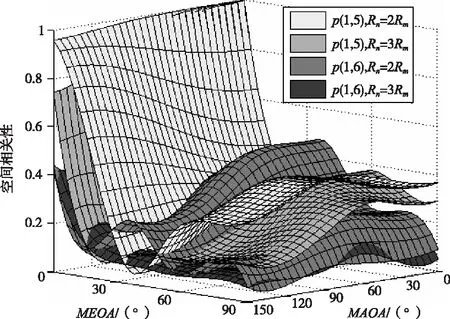
图6 平均中心到达角MAOA和MEOA对空间相关性的影响

4.2 多天线容量分析

图7示电磁信号的水平以及竖直扩展角AS和ES对线性ULA以及本文提出的天线阵列结构的信道容量的影响，从图中可以发现，在相同的AS以及ES取值范围内，本文提出的同心圆天线阵列的信道容量的取值范围远远大于线性天线结构的取值范围，从而反映出同心圆天线阵列比线性更为理想的信道容量。以上的研究结果与文献[11]的研究结果相吻合，进一步验证本节研究分析的正确性。

图8示电磁信号的平均中心到达角MAOA和MEOA对圆形UCA以及本文提出的天线阵列结构的信道容量的影响。从图中可以发现，当电磁信号的平均中心到达角MAOA发生变化时，信道容量几乎不发生改变，而MEOA增大时，信道容量逐渐减小。除此之外，还可以发现，在其他因素保持不变的情况下，同心圆天线阵列与圆形天线阵列相比可以呈现一种较为理想的信道容量，这也表明了本文提出的新型同心圆天线阵列结构的优越性，存在一定的研究意义。

图7 扩展角AS和ES对信道容量的影响

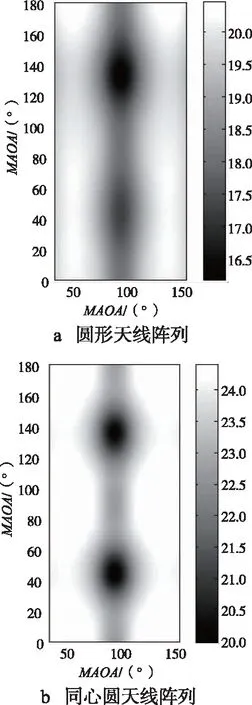
图8 平均中心到达角MAOA和MEOA对信道容量的影响

5 结束语

本文综合过去关于无线通信中天线阵列的研究，提出了三维信道模型下的新型同心圆环天线阵列，数值推导了空间相关性函数的通用表达式与阵元间距、平均中心到达角以及扩展角的关系。通过MATLAB数值仿真表明，伴随着阵元间距的增加，信道的容量逐渐增大，并且仿真结果表明与线性ULA、圆形UCA天线阵列相比，本文提出的同心圆阵列结构具有较大的信道容量，验证了本文的研究意义，促进了多天线系统的研究以及无线通信的发展。

参考文献：

[1]KAREDAL J，ALMERS P，JOHANSSON A J，et al. A MIMO channel model for wireless personal area networks[J]. IEEE Trans. Communications，2010，9(1)：245-255.

[2]付景兴，杨大成，常永宇. 信道相关性对多入多出系统性能的影响[J]. 北京邮电大学学报，2003，26(1):23-27.

[3]兰海燕，杨莘元，谭枫. 微小区MIMO信道模型的相关性分析[J]. 计算机工程，2010，36(1):99-101.

[4]孙君，袁东风. 不同传输环境下MIMO信道的空间相关性的研究[J]. 电子与信息学报，2008，30(11)：2580-2583.

[5]SALZ J，WINTERS J H. Effect of fading correlation on adaptive arrays in digital mobile radio[J]. IEEE Trans. Veh. Technol. Proc.，1994，43(4):1049-1057.

[6]魏旻，龚耀寰. MIMO 中微小区空时相关信道模型的相关性分析[J]. 系统工程与电子技术，2006，28(7)：973-984.

[7] 范文兵，赵龙贺. 单环模型下三维多极化天线MIMO信道建模[J]. 电视技术，2013,37(23)：179-182.

[8]YONG S K，THOMPSON J S. Three dimensional spatial fading correlation models for compact MIMO receivers[J]. IEEE Trans. Communications,2005,4(6):2856-2869.

[9]王月瑜,郭黎利. 三维接收天线阵列信道模型下的空域相关性[J]. 计算机工程,2008,34(12)：9-12.

[10]LEE J H，LI S I. Three-dimensional spatial correlation characteristics of concentric ring antenna array systems[C]//Proc. 17th Conference on Digital Signal Processing. Corfu，Greece：IEEE Press，2011：1-6.

[11]陈常山,张申,魏培. 基于量子粒子群算法的MIMO信道容量优化[J]. 电视技术，2012,36(23)：76-82.

Study of Uniform Concentric Ring Array in Three-Dimensional Spatial Channel Model

CHEN Zhongliang1，PAN Hao2

(1.HuanghuaiUniversity,HenanZhumadian463000,China；2.ComputerSchool，WuhanUniversity，Wuhan430072，China)

A new digital uniform concentric circular array in a three-dimensional spatial channel model is proposed in this paper，and the general spatial correlation expressions of channel model with the impact of azimuth spread and elevation spread，mean azimuth of arrival and mean elevation of arrival are derived. Comparisons among the uniform linear array，uniform circular array and the uniform concentric circular array show the ideal performance of uniform concentric circular array，that promotes the research of the statistical channel models.

uniform concentric circular array；uniform linear array；uniform circular array；spatial fading correlation.

2013年河南省科技发展计划项目(132102210463)

TN929.5

A

10.16280/j.videoe.2015.01.019

2014-06-26

【本文献信息】陈中良，潘浩.基于三维空间信道的同心圆天线阵列模型研究[J].电视技术,2015，39(1).

陈中良(1980— )，硕士，实验师，主研软件技术、计算机网络；

潘 浩，硕士,讲师，主要研究方向为计算机网络应用。

责任编辑：薛 京