时滞机床颤振模型的稳定性与Hopf分支分析

杨纪华, 张二丽, 刘 媚(. 宁夏师范学院 数学与计算机科学学院, 宁夏 固原 756000;2. 北京师范大学 数学科学学院, 北京 00875; . 郑州财经学院 计算机系, 河南 郑州 45000)



时滞机床颤振模型的稳定性与Hopf分支分析

杨纪华1,2, 张二丽3, 刘 媚1
(1. 宁夏师范学院 数学与计算机科学学院, 宁夏 固原 756000;2. 北京师范大学 数学科学学院, 北京 100875; 3. 郑州财经学院 计算机系, 河南 郑州 450001)

从模型线性化方程的特征方程根的分布分析入手,讨论模型平衡点的稳定性,确定平衡点的线性稳定性区域,当模型中时滞经过一系列临界值时,模型在平衡点附近经历Hopf分支,时滞较大,出现混沌吸引子,数值模拟验证了结论.

时滞; 稳定性; Hopf分支; 混沌吸引子

1 预备知识及模型建立

机床是金属切削加工时的主要工具,在机床加工过程中,刀具和工件所组成的系统中存在着不可避免的振动现象.一般把机床切削加工过程中工件和刀具之间的相对自激振动称为“颤振”[1].在机床的加工过程中,颤振会导致一系列不好的影响,有时甚至会带来非常严重的后果,例如,颤振会对零部件的加工质量有影响,严重时甚至会使被加工的零部件报废,还会引起崩刃等等,因此对机床加工过程中颤振问题的研究是当代学者和工程技术人员研究的热点之一[2-6].本文从稳定性与分支的角度,主要运用特征值方法来研究具时滞的机床颤振模型[7-8],并借鉴文献[9-10]中的方法,探讨机床颤振模型的稳定性和Hopf分支的存在性.

2004年,R.Szalai等[11]研究了高速铣床的动力学特性,研究认为参与切削的时间和未参加切削的时间的比值是一个小量.在这种情况下,有关机床振动的传统再生颤振模型被简化为一个离散的数学模型,其对应的非线性模型首先是由M. A. Davies等[12]建立的.虽然建立的非线性模型很简单,但很接近实际.2007年,D. A. W. Barton等[13]又在此基础上提出了一个更准确的数学模型

(1)

其中,m是模态质量,Fx和Fy分别是沿x和y方向的切割力,cx和cy分别是沿x和y方向的模态阻尼,kx和Ky分别是沿x和y方向的模态刚度,Kx和Ky分别是沿x和y方向的切削系数,ω是切削宽度,h是切削厚度,p是一个指数.

在这个模型中,假设刀具从来没有离开过工件.由于再生颤振的影响,h不是一个常量.设ν是进给速度,τ是时滞,则有

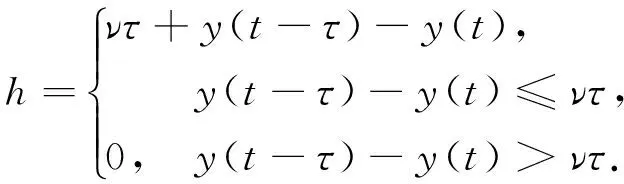
(2)

另外

RΩτ=2πR+x(t)-x(t-τ),

(3)

其中,ω是主轴转速,R是工件半径.由(1)～(3)式可得

(4)

本文不考虑机床刀具末端的螺旋角,并假设机床刀具具有对称性,即cx=xy=a,kx=ky=b,则方程(4)变为

(5)

2 平衡点的稳定性和Hopf分支存在性分析

(7)

显然,当τ=0时,方程(6)的平衡点(x0,φ0,y0,ψ0)是局部渐近稳定的.为了讨论方便,记

M

N

引理 2.1 (i) 如果M2-N<0,或者M>0且N>0,则方程(7)没有纯虚根;

(ii) 如果M2-N=0且M<0,或者N<0,则当τ=τj时,方程(7)有一对简单纯虚根±iβ0,其中

(8)

(iii) 如果M<0,M2-N>0且N>0,则当τ=τ1j(或τ=τ2j)时,方程(7)有一对简单纯虚根±iβ1(或±iβ2),其中

(9)

证明λ=iβ(β>0)是方程(7)的根的充要条件是β满足

(10)

平方相加可得

(11)

进而可得

(12)

(i) 如果M2-N<0,或M>0且N>0,则方程(11)没有正实根,从而方程(7)无纯虚根;

(iii) 如果M<0,M2-N>0且N>0,方程(11)仅有2个正根

令τ1j和τ2j如(9)式所定义,则(τ1j,β1)和(τ2j,β2)是方程(10)的解,即λ=±iβ1(或λ=±iβ2)是τ=τ1j(或τ=τ2j)时方程(7)的一对纯虚根.

由隐函数定理,存在ε0>0,使得当|τ-τj|<ε0时,方程(7)有一对共轭根λ(τ)=α(τ)±iβ(τ),且满足α(τj)=0,β(τj)=β0.同理,存在εk>0(k=1,2),使得当|τ-τkj|<εk(k=1,2)时,方程(7)有一对共轭根λ(τ)=α(τ)±iβ(τ),且满足α(τkj)=0,β(τkj)=βk(k=1,2).

引理 2.2 如果M2-N>0,则

证明 对方程(7)两边关于τ求导得

所以

其中

i=0,1,2,

由M2-N>0可得结论成立.

引理 2.3[15]设f(λ,τ)=λ2+a1λ+a2λe-λτ+a3e-λτ+a4,则当τ变化时,f(λ,τ)在右半平面上的零点重数之和当且仅当有零根穿过虚轴时才发生变化,其中a1,a2,a3,a4∈R且τ>0.

由引理2.1～2.3和文献[16]中第11章的定理1.1,可以得到如下2个定理.

定理 2.1 如果M2-N<0,或者M>0且N>0,则对任意τ≥0,系统(5)的平衡点是渐近稳定的.如果N<0有:

(i) 当τ∈[0,τ0)时,系统(5)的平衡点是渐近稳定的;

(ii) 当τ>τ0时,系统(5)的平衡点是不稳定的;

(iii) 当τ=τj(j=0,1,2,…)时,系统(5)在平衡点附近经历Hopf分支.

定理 2.2 如果M<0,M2-N>0且N>0有

时,系统(5)的平衡点不稳定;

(ii) 当τ=τkj(k=1,2;j=0,1,2,…)时,系统(5)在平衡点附近经历Hopf分支.

3 数值模拟及结论

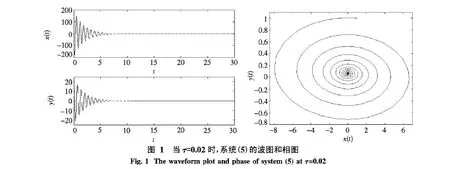
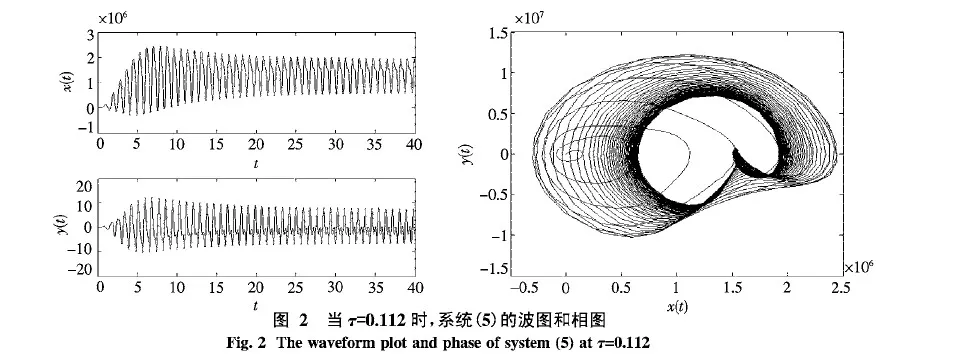
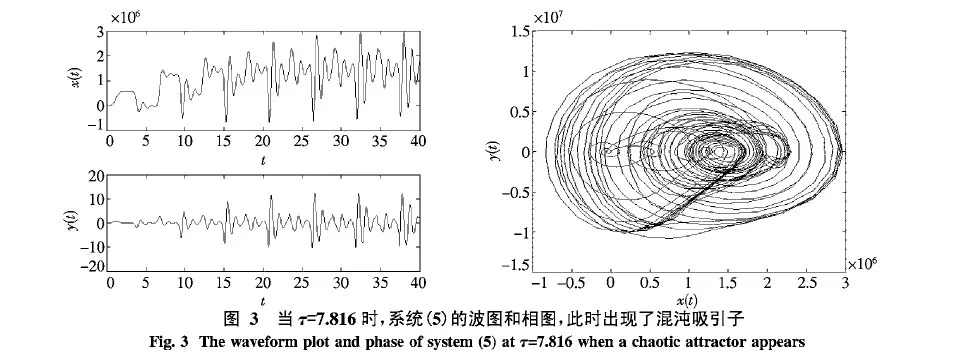
在方程(5)中,取a=18.13,b=220,Kx=55 000,Ky=20 000,d=0.02,m=2.586,p=0.75,r=0.05和ν/ω=0.5.计算可得β0=7.692 8,τ0=0.116 4.根据定理2.1知,当τ=0.02时,系统(5)的平衡点是局部渐近稳定的,如图1所示.当τ=0.112时,系统(5)在平衡点附近经历了Hopf分支,如图2所示.当τ=7.816时,系统(5)的平衡点是不稳定的.此时出现了混沌吸引子,如图3所示.

本文研究时滞机床颤振模型的动力学行为.以时滞为参数,应用特征值方法对该模型的稳定性进行了分析,发现系统(5)中存在稳定性开关,并给出了系统(5)存在Hopf分支的充分条件.计算机的模拟结果很好地支持了本文的理论结果.理论分析和计算机模拟表明,时滞在机床颤振模型中起着非常重要的作用.数值模拟揭示了时滞对机床颤振系统的稳定、振荡和混沌状态的影响(见图1～3).即使是在线性稳定边界上,混沌状态也可以使机床系统产生颤振.图1～3表明时滞可以调节系统的混沌状态,通过选取合适的时滞,可以使系统(5)从混沌状态转化为稳定状态或周期循环状态,所以在机床系统中考虑时滞的影响是很必要的.

[1] 赵德敏. 非线性颤振系统的分岔与混沌[D]. 天津:天津大学,2009.

[2] Faassen R P H. An improved tool path model including periodic delay for chatter prediction in milling[J]. J Comput Nonlinear Dyn,2007,35(2):167-179.

[3] 郭杰,陈健生,向守兵,等. 基于机器视觉的精密铸铁平板刮研质量检测[J]. 四川师范大学学报:自然科学版,2013,36(5):787-791.

[4] Xie Q Z, Zhang Q C, Han J X. Hopf bifurcation for delay differential equation with application to machine tool chatter[J]. Appl Math Mod,2012,36(8):3803-3812.

[5] Wan M, Zhang W H, Dang J W. A unified stability prediction method for milling process with multiple delays[J]. Inter J Mach Tool Manuf, 2010,50(1):29-41.

[6] Chaitanya V. Stability analysis of structurally unstable man-machine system involving time delays[J]. Nonlinear Analysis:RWA,2005,6(5):845-857.

[7] 李坤琼,刘双,朱长荣. 一类新三维混沌系统的脉冲控制和Hopf分支[J]. 四川师范大学学报:自然科学版,2013,36(5):708-711.

[8] Hale J K. Theory of Functional Differential Equations[M]. New York:Springer-Verlag,2003.

[9] Jiang W H, Wang H B, Wei J J. A study of singularities for magnetic bearing system with time delays[J]. Chaos, Solitons and Fractals,2008,36(4):715-719.

[10] 赵君平,于育民. 一类病菌与免疫系统作用模型的定性分析[J]. 四川师范大学学报:自然科学版,2012,35(2):202-208.

[11] Szalai R, Stepan G, Hogan S J. Global dynamics of low immersion high speed milling[J]. J Manuf Sci Eng,2004,7(1):1069-1077.

[12] Davies M A, Pratt J R, Dutterer B. Stability prediction of low radial immersion milling[J]. J Manuf Sci Eng,2002,124(2):217-225.

[13] Barton D A W, Insperger T, Stepan G. Criticality of Hopf bifurcation in state-dependent delay model of turning processes[J]. Internat J Nonlinear Mech,2008,43(2):140-149.

[14] Wiggins S. Introduction to Applied Nonlinear Dynamical System and Chaos[M]. New York:Springer-Verlag,1996.

[15] Ruan S G, Wei J J. On the zeros of transcendental function with applications to stability of delay differential equation with two delays[J]. Dyn Contin Discrete Impuls Syst,2003,10(6):863-874.

[16] Hale J K, Lunel S V. Introduction to Functional Differential Equation[M]. New York:Springer-Verlag,1993.

2010 MSC：34C07

(编辑 郑月蓉)

Stability and Hopf Bifurcation Analysis of Machine Tool Chatter Model with Time Delay

YANG Jihua1,2, ZHANG Erli3, LIU Mei1
(1.SchoolofMathematicsandComputerScience,NingxiaNormalCollege,Guyuan756000,Ningxia;2.SchoolofMathematicalScience,BeijingNormalUniversity,Beijing100875;3.DepartmentofComputerScience,ZhengzhouInstituteofFinanceandEconomics,Zhengzhou450001,Henan)

The stability of the equilibrium is discussed by analyzing the characteristic equation of the linearized system of original system at the equilibrium, the regions of linear stability of equilibrium are given. It is found that Hopf bifurcation exists when the delay passes through a sequence of critical values, the chaotic attractor appears when delay increases further. In the end, the results are confirmed by numerical simulations.

time delay; stability; Hopf bifurcation; chaotic attractor

2013-04-22

国家自然科学基金(11361046)、宁夏科技支撑计划(宁科计字[2015]26号(4))、宁夏自然科学基金(NZ13213)和宁夏高等学

杨纪华(1983—),男,讲师,主要从事时滞微分方程的稳定性与分支的研究,E-mail:jihua1113@163.com

O175.14

A

1001-8395(2015)06-0838-05

10.3969/j.issn.1001-8395.2015.06.009

校科研项目(宁教高[2014]222号(17))