含非线性扰动的变时滞随机微分系统的均方渐近稳定性

柴双龙, 李树勇(1. 四川师范大学 数学与软件科学学院, 四川 成都 610066; 2. 绵阳师范学院 数学与计算机科学学院, 四川 绵阳 621006)



含非线性扰动的变时滞随机微分系统的均方渐近稳定性

柴双龙1,2, 李树勇1*
(1. 四川师范大学 数学与软件科学学院, 四川 成都 610066; 2. 绵阳师范学院 数学与计算机科学学院, 四川 绵阳 621006)

研究一类含有非线性扰动的变时滞随机系统的均方渐近稳定性问题.通过构造Lyapnov-Krasovskii泛函,运用It公式,借助Lyapunov稳定性理论思想,利用Riccati矩阵方程相关知识,建立该系统的均方渐近稳定的充分条件.最后给出数值实例,验证所得结果的有效性.

非线性扰动; 变时滞; 随机微分系统; Riccati矩阵方程; 均方渐近稳定

1 预备知识

近几十年来,时滞随机微分系统的稳定性研究一直是人们关注的重点,并取得了丰硕的研究成果[1-13],建立了时滞随机微分系统稳定性的技巧,如Riccati矩阵方程[3]、Moon不等式技巧[4]、比较原理[5]、Lasalle不变原理[6]、线性矩阵不等式(LMI)[7-9]、自由权矩阵[10-11]、非负半鞅收敛定理[12]、不等式分析技巧[13].Riccati矩阵方程是研究时滞随机系统的一个有力工具.利用Riccati矩阵方程性质研究稳定性能够巧妙的构造出Lyapnov泛函,以克服构造Lyapnov泛函不易的困难.文献[3]展示了利用Riccati方程研究时滞随机微分系统均方渐近稳定性的优点.本文利用Riccati矩阵方程的性质研究一类含有非线性扰动的变时滞随机系统的均方渐近稳定性,通过构造Lyapnov-Krasovskii泛函,运用It公式,引入适当的自由权矩阵,借助Lyapunov稳定性定理获得系统的均方渐近稳定的充分条件,通过例子显示本文方法的有效性.

2 系统描述

考虑具有非线性扰动的时变时滞随机微分系统

(1)

其中,x(t)∈Rn是状态向量;A,B∈Rn×n,C,D∈Rm×n是不确定的常数矩阵,时变向量函数f:[0,+∞)×Rn×Rn→Rn,w(t)是定义在具有自然滤波{Ft}t≥0且完备的概率空间(Ω,F,P)上的1维标准Brownian运动;初始条件φ(t)是定义在[-τ,0]上的连续向量值函数.τ(t)表示时变时滞,并满足如下条件:

变时滞τ(t)可微并满足

(2)

其中,τ是正常数,μ是常数.

假设矩阵B满足条件

(3)

时变向量函数f(t,x(t),x(t-τ(t)))是具有系统当前状态和时滞状态的非线性扰动,满足下面的不等式条件

(4)

其中αi≥0(i=0,1).

3 基本准备

考虑时滞随机系统

dx(t)=h(t,xt)dt+g(t,xt)dw(t),t>0,

(5)

其中,x(t)∈Rn,w(t)是(Ω,F,P)上m维的布朗运动,h:R+×C|→Rn,g:R+×C|→Rn×m.(5)式的初始函数为x(s)=φ(s)∈Rn是随机变量,s∈[-τ,0],这里τ为正常数.取泛函V∈C1,2(R+×C;R+),通过定义(5)式生成的微分算子LV为

其中Tr表示矩阵的迹.

本文的目的是研究(1)式在满足条件(2)～(4)式的均方渐近稳定性.为此,需要引用下列引理.

引理3.1[3]若存在一个泛函V(t,xt):[0,∞)×C→R+满足如下条件

ELV(t,xt)≤ExT(t)D(t)x(t)+

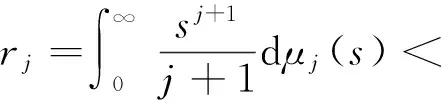
矩阵

其中K是以ki,(i=1,…,n)为对角元素的对角型矩阵,若G(t)是一致负定矩阵.即:xTG(t)x≤-c|x|2,c>0,x∈Rn,则(1)式的零解是均方渐近稳定的.

引理3.2[13]对具有适当维数的任意向量a、b及任意对称正定矩阵X>0有

aTb+bTa≤aTXa+bTX-1b.

4 主要结果

定理4.1 在假设(2)和(4)式成立的条件下,如果存在适当维数实对称矩阵P>0,以及任意n×n维的正定矩阵R1、R2、R3、Q,使得Riccati矩阵方程

(6)

成立,且

(7)

(8)

则具有非线性扰动(4)式,满足时滞约束条件(2)式的变时滞随机系统(1)式是均方渐近稳定的.

证明 构造如下Lyapunov-Krasovskii泛函

V(t,xt)=xT(t)Px(t),

(9)

其中P∈Rn×n是对称正定矩阵.

LV(t,xt)=[Ax(t)+Bx(t-τ(t))+

f(t,x(t),x(t-τ(t)))]TPx(t)+xTP[Ax(t)+

Bx(t-τ(t))+f(t,x(t),x(t-τ(t)))]+[Cx(t)+Dx(t-τ(t))]TP[Cx(t)+Dx(t-τ(t))]=

xT(t)[ATP+PA+CTPC]x(t)+

xT(t-τ(t))DTPDx(t-τ(t))+

xT(t-τ(t))BTPx(t)+xT(t)PBx(t-τ(t))+

xT(t-τ(t))DTPCx(t)+

xT(t)CTPDx(t-τ(t))+fT(t,x(t),x(t-

τ(t)))Px(t)+xTPf(t,x(t),x(t-τ(t))).

(10)

由引理3.2,若取a=x(t-τ(t)),b=BTPx(t),知对任意的对称正定矩阵R1使得下面不等式成立

xT(t-τ(t))BTPx(t)+xT(t)PBx(t-τ(t))≤

xT(t-τ(t))R1x(t-τ(t))+

(11)

若取a=x(t-τ(t)),b=DTPCx(t),则对任意的对称正定矩阵R2有下面不等式成立

xT(t-τ(t))DTPCx(t)+xT(t)CTPDx(t-τ(t))≤

xT(t-τ(t))R2x(t-τ(t))+

(12)

若取a=f(t,x(t),x(t-τ(t))),b=Px(t),可得对任意的对称正定矩阵R3有

fT(t,x(t),x(t-τ(t)))Px(t)+

xTPf(t,x(t),x(t-τ(t)))≤

fT(t,x(t),x(t-τ(t)))R3f(t,x(t),

(13)

由非线性扰动条件(4)式有

(14)

综合(11)～(14)式可得

ELV(t,xt)≤E{xT(t)[ATP+PA+CTPC+

R1+R2+α12R3]x(t-τ(t))}.

由(6)～(8)式有

(15)

成立,则由引理3.1知,(1)式的零解是均方渐近稳定的,即只要(6)～(8)式成立,则具有非线性扰动(4)式,满足时滞约束条件(2)式的变时滞随机系统(1)式是均方渐近稳定的.定理得证.

推论 4.1 在假设(2)和(4)式成立的条件下,如果存在n×n维实对称矩阵P>0,以及任意的n×n维正定矩阵R1、R2、R3、Q,使得Riccati矩阵方程

ATP+PA+CTPC+PR1P+CPR2PC+

(16)

成立,且

ATP+PA+CTPC+PR1P+

(17)

则具有非线性扰动(4)式,满足时滞约束条件(2)式的变时滞随机系统(1)式是均方渐近稳定的.

证明 利用引理3.2,对于R1,取a=Px(t),b=Bx(t-τ(t));对于R2,取a=PCx(t),b=Dx(t-τ(t)).替换(11)和(12)式得

ELV(t,xt)≤E{xT(t)[ATP+PA+CTPC+

由(16)～(18)式知

D(t)=ATP+PA+CTPC+PR1P+

(19)

成立.则由引理3.1知,(1)式的零解是均方渐近稳定的,即只要(16)～(18)式成立,则有(2)式,满足(2)式的变时滞随机系统(1)是均方渐近稳定的.定理得证.

定理 4.2 若常数μ<0,在假设(2)～(4)式成立的条件下,如果存在适当维数实对称矩阵P,H4,H5,H6>0,以及任意n×n维的正定矩阵H1、H2、H3、Q,使得Riccati矩阵方程

P(A+B)+(A+B)TP+CTPC+H1+

成立,则有(4)式,满足时滞约束条件(2)和(3)式的变时滞随机系统(1)是均方渐近稳定的.

证明 现将系统(1)改写为如下的中立型时滞随机系统

(21)

构造Lyapunov-Krasovskii泛函V(t,xt)=V1(t,xt)+V2(t,xt),其中

V1(t,xt)=zT(t)Pz(t),

计算V1(t,xt)沿着(21)式的轨线生成的算子LV1(t,xt).

LV1(t,xt)=zT(t)P[(A+B)x(t)+

x(t-τ(t)))]TPz(t)+[Cx(t)+

Dx(t-τ(t))]TP[Cx(t)+Dx(t-τ(t))]=

xT(t)[P(A+B)+(A+B)TP+CTPC]x(t)+

xT(t-τ(t))DTPDx(t-τ(t))+

xT(t)CTPDx(t-τ(t))+

xT(t-τ(t))DTPCx(t)+

xT(t-τ(t))BTPx(t)]+

xT(t)Pf(t,x(t),x(t-τ(t)))+fT(t,x(t),

x(t-τ(t)))Px(t)+

xT(t)(A+B)TPBx(s)]ds+

xT(t-τ(t))BTPBx(s)]ds+

fT(t,x(t),x(t-τ(t)))PBx(s)]ds.

(22)

利用引理3.2,对于任意n×n维的正定矩阵H1:取a=x(t),b=CTPDx(t-τ(t));H2:取a=x(t),b=PBx(t-τ(t));H3:取a=x(t),b=Pf(t,x(t),x(t-τ(t)));H4:取a=x(s),b=BTP(A+B)x(t);H5:取a=x(s),b=BTPBx(t-τ(t));H6:取a=x(s),b=BTPf(t,x(t),x(t-τ(t))),得到不等式

xT(t)CTPDx(t-τ(t))+

xT(t-τ(t))DTPCx(t)≤xT(t)H1x(t)+

(24)

xT(t)Pf(t,x(t),x(t-τ(t)))+fT(t,x(t),

x(t-τ(t)))Px(t)≤xT(t)H3x(t)+fT(t,x(t),

xT(t)(A+B)TPBx(s)]ds≤

(26)

xT(t-τ(t))BTPBx(s)]ds≤

fT(t,x(t),x(t-τ(t)))PBx(s)]ds≤

(28)

由非线性扰动条件(4)式有

(29)

(30)

综合(22)～(30)式可得

ELV1(t,xt)≤E{xT(t)[P(A+B)+(A+B)TP+

(31)

沿着系统(21)式的轨线计算生成的算子LV2(t,xt),

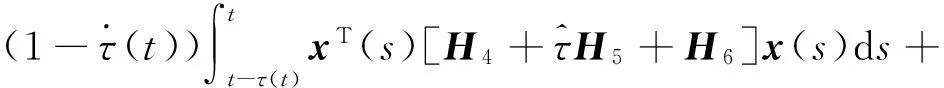
xT(t)Ωx(t)-xT(t-τ(t))Ωx(t-τ(t)).

(32)

由(31)和(32)式得

ELV(t,xt)≤E{xT(t)[P(A+B)+

由条件(20)式知

G(t)=D(t)=P(A+B)+(A+B)TP+

成立.则由引理3.1知,系统(1)式的零解是均方渐近稳定的.定理得证.

P(A+B)+(A+B)TP+CTPC+

(33)

成立.则具有非线性扰动(4)式,满足条件(2)和(3)式的变时滞随机系统(1)式是均方渐近稳定的.

注 1 推论4.2的证明类似于定理4.2.当α0=α1=0时,定理4.1和4.2得到了无非线性扰动的均方渐近稳定的充分条件.

5 数值实例

考虑如下具有非线性扰动的变时滞随机微分系统

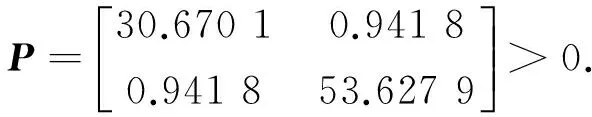
验证了本文方法的有效性.

[1] Mao X R. Stochastic Differential Equation and Their Applications[M]. Chichester:Horwood,1997.

[2] 胡适耕,黄乘明,吴付科. 随机微分方程[M]. 北京:科学出版社,2008.

[3] Shaikhet L. Lyapunov Functionals and Stability of Stochastic Functional Differential Equations[M]. New York:Spinger International Publishing,2013.

[4] Huang H, Ho D W C. Delay-dependent robust control of uncertain stochastic fuzzy with time-varying delay[J]. ITE Control Theory Appl,2007,1(4):1075-1085.

[5] 江明辉,沈轶,蹇继贵. 时滞随机线性大系统的指数稳定性[J]. 系统工程学报,2005,20(6):564-569.

[6] 江明辉,沈轶,廖晓昕. 不确定中立型线性随机时滞系统的鲁棒稳定性[J]. 应用数学和力学,2007,28(6):741-748.

[7] Chienyu L, Gwojia J, Tejen S A. An LMI-based approach for robust stabilization of uncertain stochastic systems with time-varying delays[J]. IEEE Transactions on Automatic Control,2003,48(2):286-289.

[8] Chienyu L, Tejen S, Jason S H T. On robust stabilization of uncertain stochastic time-delay systems:an LMI-based approach[J]. J Franklin Institute,2005,342(5):473-487.

[9] Zhao X D, Ling M X, Zeng Q S. Delay-dependent robust control for uncertain stochastic systems with Markovian switching and multiple delays[J]. J Systems Engineering Electronics,2010,21(2):287-295.

[10] 吴立刚,王常虹,高会军,等. 时滞不确定随机系统基于参数依赖Lyapunov函数的稳定条件[J]. 控制理论与应用,2007,24(4):607-612.

[11] 刘宝晶,赵立英. 时滞随机系统的稳定性分析[J]. 计算技术与自动化,2010,29(2):5-8.

[12] 赵亮,李树勇,张秀英,等. 一类含连续分布时滞的随机Hopfiled神经网络模型的几乎必然指数稳定性和p阶矩指数稳定性[J]. 四川师范大学学报:自然科学版,2013,36(3):1-5.

[13] Cao Y Y, Sun Y X, Cheng C W. Delay-dependent robust stabilization of uncertain systems with multiple state delays[J]. IEEE Transactions on Automatic Control,1998,43(11):1608-1612.

2010 MSC：65C30; 34K20; 60H35

(编辑 郑月蓉)

Asymptotically Mean-Square Stability for Stochastic Differential Systems with Nonlinear Perturbation and Time-Varying Delay

CHAI Shuanglong1,2, LI Shuyong2
(1.CollegeofMathematicsandSoftwareScience,SichuanNormalUniversity,Chengdu610066,Sichuan;2.InstituteofMathematicsandComputerScience,MiangyangNormalCollege,Mianyang621006,Sichuan)

In this paper, the asymptotically mean-square stability for stochastic differential systems with nonlinear perturbation and time-varying delay is concerned. By establishing a Lyapunov-Krasovskii functional, using the Itformula and by virtue of Lyapunov stability theory, the sufficient conditions for the asymptotically mean-square stability of the system are obtained in terms of the matrix Riccati equation. Finally, the numerical example is provided to demonstrate the effectiveness of the result received.

nonlinear perturbation; time-varying delay; stochastic differential systems; matrix Riccati equation; asymptotically mean-square stability

2014-10-09

国家自然科学基金(11271270)和四川省教育厅自然科学重点课题(10ZA125)

O211.63

A

1001-8395(2015)06-0791-06

10.3969/j.issn.1001-8395.2015.06.001

*通信作者简介：李树勇(1964—),男,教授,主要从事时滞随机微分系统稳定性的研究,E-mail:shuyongli@263.net