含一阶导数项的三阶周期边值问题解的存在唯一性
白 婧, 李永祥(西北师范大学 数学与统计学院, 甘肃 兰州 730070)
含一阶导数项的三阶周期边值问题解的存在唯一性
白 婧, 李永祥*
(西北师范大学 数学与统计学院, 甘肃 兰州 730070)
三阶常微分方程的周期边值问题一直是常微分方程研究的热点.研究非线性项含一阶导数项的三阶周期边值问题
三阶周期边值问题; 存在性与唯一性; Leray-Schauder不动点定理
本文利用Leray-Schauder不动点定理,讨论了三阶周期边值问题
(1)
解的存在唯一性.其中I=[0,ω],f:I×R2→R连续.
三阶常微分方程周期边值问题是微分方程中人们关注的问题,在这方面已有很多研究成果,见文献[1-14].A. Cabada[1]用上下解方法获得了三阶周期边值问题
u‴(t)=f(t,u(t)),a≤t≤b,
u(i)(a)-u(i)(b)=λi,i=0,1,2
(2)
解的存在性.其中f为Carathéodory函数,a、b、λi∈R.L. Kong[2]等利用Schauder不动点定理考虑了三阶周期边值问题
f满足下列条件:
(A1)f(t,u)为[0,2π]×(0,+∞)上的非负函数,并且f(t,u)在[0,2π]上可积;
(A2) 对∀t∈[0,2π],u>0,f(t,u)不增且满足

u‴(t)+αu″(t)+βu′(t)=
f(t,u(t)),t∈[0,2π],
(4)
其中α、β为正常数,在满足特定的条件下,利用锥上的Krasnoselskii不动点定理,得出方程(4)正周期解的存在性.
在上述文献中非线性均不含导数项,本文在非线性含有一阶导数项的情形下,利用Leray-Schauder不动点定理得到方程(1)解的存在唯一性.
1 预备工作

对∀h∈L2(I),a0,a1≠0,考虑三阶线性周期边值问题
在文献[8]中有:
引理 1 假设如下条件成立
|k∈Z}=Ø,
则线性周期边值问题(5)有唯一解u:=Th∈W3,2(I),且解算子T:L2(I)→W3,2(I)为线性全连续算子.
又由嵌入W3,2(I)W1,2(I)的紧性,则T:L2(I)→W1,2(I)为线性全连续算子.
W1,2(I)中按范数
‖
构成Banach空间,为方便起见,用X表示该Banach空间.
引理 2 设a0,a1≠0,则线性周期边值问题(5)的解算子T:L2(I)→X的范数满足
‖T‖L(L2(I),X)≤M,
其中
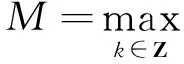


(6)
其中
且有Parseval等式
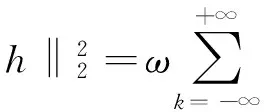
成立.因此
u=Th∈W3,2(I)
也可展为Fourier级数
(7)
所以
u‴
从而
u‴(t)+a1u′(t)+a0u(t)=
(8)
由Fourier展式的唯一性
(9)
所以
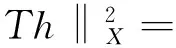


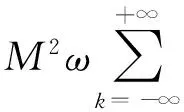
(10)
因此,‖T‖L(L2(I),X)≤M.
引理 3[9](Leray-Schauder不动点定理) 设F:X→X全连续,若方程簇
λF(x)=x, 0<λ<1
的解集在X中有界,则F在X中有不动点.
2 主要结论
定理 1 假设下列条件成立:
(H1) 存在常数α0、α1≥0及C>0,使得
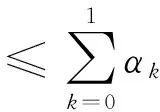
(H2)M(α0+α1)<1;
则周期边值问题(1)至少存在一个解.
证明 令
F(u)(t)=f(t,u(t),u′(t))+
a1u′(t)+a0u(t),
(11)
则F:X→L2(I)连续,把有界集映为有界集.因此,复合算子A=T∘F:X→X为全连续算子.根据算子T的定义,三阶周期边值问题(1)的解等价于算子A的不动点.对A应用Leray-Schauder不动点定理,考虑方程簇
u=λAu, 0<λ<1,
(12)
要证同伦簇方程的解集在X中有界.
设u∈X为方程簇(12)中某个方程的解,则
u=T(λF(u))
为
h=λF(u)
相应的线性方程(5)的解.由假设条件(H1)得如下的范数估计

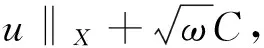
(13)
所以
‖u‖X=‖Th‖X≤‖T‖L(L2(I),X)‖h‖2≤
M‖h‖2 (14) 故 (15) 因此,同伦簇方程(12)的解集在X中有界.由引理3中Leray-Schauder不动点定理知,算子A在X中存在不动点u,u为三阶周期边值问题(1)的解. 下面讨论三阶周期边值问题(1)解的存在唯一性.为此,需加强条件(H1)为(H1)′存在常数α0、α1≥0,使得 (16) 定理 2 假设条件(H1)′、(H2)成立,则三阶周期边值问题(1)存在唯一解. 证明 由定理1知三阶周期边值问题(1)至少存在一个解.设u1、u2为三阶周期边值问题(1)的2个解.令 u=u2-u1, 则 u=T(F(u2)-F(u1)) 为 h=F(u2)-F(u1) 对应的线性周期边值问题(5)的解.因此,由引理1及假设条件(H1)′可得 (α0+α1)‖u‖X. (17) 所以 ‖u2-u1‖X=‖T(F(u2)-F(u1))‖X≤ ‖T‖L(L2(I),X)‖F(u2)-F(u1)‖2≤ M(α0+α1)‖u2-u1‖X, (18) 从而 ‖u2-u1‖X=0, 即 u2=u1. 所以周期边值问题(1)存在唯一解. [1] Cabada A. The method of lower and upper solutions for second, third, fouth and higher order boundary value problems[J]. J Math Anal Appl,1994,185:302-320. [2] Kong L, Wang S, Wang J. Positive solution of a singular nonlinear third-order periodic boundary value problem [J]. J Comput Appl Math,2001,132:247-253. [3] Sun J, Liu Y. Multiple positive solutions of sigular third-order periodic boundary value problem [J]. Acta Math Sci,2005,25:81-88. [4] Feng Y. On the exixtence and multiplicity of positive periodic solutions of a nonlinear third-order equation[J]. Appl Math lett,2009,22:1220-1224. [5] Chu J, Zhou Z. Positive solutions for singular non-linear third order periodic boundary value problems[J]. Nonlinear Anal,2006,64:1528-1542. [6] Li Y. Positive periodic solutions for fully third-order ordinary differential equations [J]. Comput Appl Math,2010,59:3464-3471. [7] 姚庆六. 变系数三阶周期边值问题的正解[J]. 吉首大学学报:自然科学版,2010,31(6):9-13. [8] Li Y. Existence and uniqueness for higher order periodic boundary value problem under spetral separarion conditions[J]. J Math Anal Appl,2006,322:530-539. [9] Ren J L, Cheng Z B, Chen Y L. Existence results of periodic solutions for third order nonlinear sigular differential equation [J]. Math Nach,2013,286:1022-1042. [10] Cheng Z B. Exixtence of positive periodic solutions for third-order differential equation with strong singularity[J]. Adv Difference Equ,2014,162:1-12. [11] Cheng Z B, Ren J L. Existence of positive periodic solution for variable-coefficient third order differential equation with singularity[J]. Math Meth Appl Sci,2014,37:2281-2289. [12] 李小龙. Banach空间非线性三阶周期边值问题的正解[J]. 应用数学,2013,26(3):652-657. [13] Wang Y, Lian H, Ge W. Periodic solutions for a second order nonlinear funtional differential equation[J]. Appl Math Lett,2007,20:110-115. [14] Li Y H, Zhang X Y. Multiple positive solutions of boundary value problems for system of nonlinear third-order differential equations[J]. J Math Res Appl,2013,3:321-329. [15] Chen L, Hu L G, Ma X D. Positive solutions to singular eigenvale problems for third-order differential equations[J]. Acta Anal Funct Appl,2012,14:377-387. [16] Deimling K. Nonlinear Functional Analysis[M]. Berlin:Springer-Verlag,1985. 2010 MSC:34A12 (编辑 余 毅) Existence and Uniqueness Result for Third-order Periodic Boundary Value Problem with the First Derivatives BAI Jing, LI Yongxiang Third-order periodic boundary value problem has always been the hot of the ordinary differential equation. In this paper, we discuss the solvability of the third-order periodic boundary value problem with nonlinear termu′,u‴(t)=f(t,u(t),u′(t)),0≤t≤ω,u(i)(0)=u(i)(ω),i=0,1,2, wheref:[0,ω]× R2→ R is a continuous function. Using the method of Fourier analysis and the perturbation technique of nonlinear term, the existence and uniqueness of solution are obtained by Leray-Schauder fixed point theorem. Since many former studies have focused on nonlinear term without derivative, our results generalize the previous conclusions. third order periodic boundary value problem; existence and uniqueness; Leray-Schauder fixed point theorem 2015-03-30 国家自然科学基金(11261053)和甘肃省自然科学基金(1208R-JZA129) O175.8 A 1001-8395(2015)06-0834-04 10.3969/j.issn.1001-8395.2015.06.008 *通信作者简介:李永祥(1963—),男,教授,主要从事非线性泛函分析的研究,E-mail:liyx@nwnu.edu.cn 其中,f:[0,ω]×R2→R连续,通过Fourier分析的方法及非线性项的扰动技巧,利用Leray-Schauder不动点定理得出解的存在性与唯一性.之前的许多研究主要集中在非线性项不含导数项的情形,对之前所得结论进行了推广.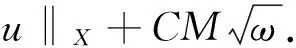
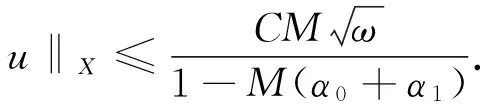
(CollegeofMathematicsandStatistics,NorthwestNormalUniversity,Lanzhou730070,Gansu)

