克里金插值参数设置对网格化结果的影响

李增涛， 高 鹏， 张三敏， 张 旭， 于峰丹

(1.西北有色地质勘查局 物化探总队，西安 710068；2.中国地质调查局 西安地质调查中心，西安 710054)



克里金插值参数设置对网格化结果的影响

李增涛1， 高 鹏2， 张三敏1， 张 旭2， 于峰丹2

(1.西北有色地质勘查局 物化探总队，西安 710068；2.中国地质调查局 西安地质调查中心，西安 710054)

为研究常用的克里金插值方法各参数对网格化结果的影响，通过应用长方体正演公式，建立模型模拟三种不同测线方向的磁测数据，计算插值数值与采样数值的绝对误差均方根值，评价网格化效果和误差。结果发现，①变基函数对克里金网格化结果影响较大，而linear和power变基函数的网格化误差较小；②网格间距对于网格化结果的影响小于变基函数的影响；③点模式、块模式和各向异性的误差稍小；④漂移模式和搜索范围参数的影响较小，可忽略不计。

克里金； 网格化； 绝对误差； 网格参数

0 引 言

地球物理数据需要进行网格化，许多学者经常使用Surfer软件的克里金插值处理数据。克里金插值的参数选择及其对网格化结果影响如何？陈欢欢等[1]对Surfer的插值方法进行了评述；刘兆平等[2]介绍了克里金网格化方法特征和应用条件，对于插值参数的具体设置及其对网格化结果的影响均未讨论；王兆国等[3]论述了网格间距对网格化精度的影响；张颖等[4]提出要注意变差函数滞后距离的设置；曾怀恩等[5]给出了变异函数理论模型参数估计的新指标，对于其他参数的设置及影响均没有提及。对比前人和已有文献可知，克里金方法的原理、特征前人多有论述，关于该方法的参数设置及其对网格化效果的影响鲜有涉及。为分析Surfer中克里金网格化参数设置对网格化结果的影响，这里通过模拟测线分别为0°、45°、150°的三种测网数据，计算插值数值与模拟值之间的误差，探讨参数设置对网格化结果的影响程度。

1 模型

研究分析Surfer中克里金网格化参数设置对网格化结果的影响，利用郭志宏等[6]、李焓等[7]给出的长方体ΔT场无解析奇点理论表达式编制程序，建立一个简单模型(图1)，地质体为一长方体，以地质体在地表的投影中心为坐标原点，长方体中心点坐标为0 m、0 m、60 m，顶面埋深为10 m，沿东西向、南北向的延伸长度分别为150 m、750 m，长方体八个拐点坐标为(-150,-750,10)、(150,-750,10)、(150,750,10)、(-150,750,10)、(-150,-750,110)、(150,-750,110)、(150,750,110)、(-150,750,110)，单位为m；磁性体磁化强度为1 000×4π×10-6SI，磁化倾角为45°，磁化偏角为90°；磁异常倾角为45°，偏角为90°，异常单位nT。分别布设测线为0°、45°、150°的平面规则测网，点线距为500 m×100 m，测网四个拐点坐标为(-2 000,-2 000)、(-2 000,2 000)、(2 000,2 000)、(2 000,-2 000)，单位为m，高程地表为10 m。对于取得的采样数据，分别采用50 m×50 m、70.7 m×70.7 m、86.6 m×86.6 m的网格距进行网格，计算插值数值与采样数值的绝对误差均方根值。

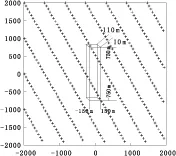
图1 模型大小和150°测网

2 变基函数的影响

表1为采用软件默认参数值时，不同变基函数网格化数值与采样数值的绝对误差均方根值，单位nT。从表1中可以看出，不同的变基函数插值结果相差较大，绝对误差均方根值的最大值约是最小值的10倍；Linear和Power是十二种变基函数中ΔT绝对误差均方根值最小的变基函数，二者的插值结果基本相同，Power的计算时长稍大于Linear的计算时长。网格间距设置适当时(采样数据点全部落在网格节点上时)，计算的ΔT绝对误差均方根值等于“0”；当采样数据点与网格节点不完全重合时，计算的ΔT绝对误差均方根值在10 nT以上。

3 漂移和点块模式的影响

在克里金方法高级选项中，有Kriging (Point点、Block块)和Drift(None无、Linear线性、Quadratic二次方程式)两种 模式供使用者选择。为研究Kriging、Drift模式的影响，这里选用测线方向为150o、45o、0o的网格数据，网格化的网格间距分别为50 m×50 m、70.7 m×70.7 m、86.6 m×86.6 m，采用Linear和Power变基函数，分别选择Point(点)、Block(块)、None Drift、Linear Drift、Quadratic Drift进行网格化，计算插值数值与采样数值的绝对误差均方根值。

从图2中可以看出，对于给定测线方向数据，当网格间距给定时，Point 模式的 ΔT绝对误差均方根值大于Block模式；Point模式下，Linear、Power变基函数插值时，无论何种Drift模式，ΔT绝对误差均方根值基本相等；Block模式下，Linear、Power变基函数插值时，Quadratic Drift的ΔT块绝对误差均方根值小于None Drift、Linear Drift模式；Drift模式对网格化结果影响小于Kriging模式。

4 斜率和各向异性的影响

克里金方法高级选项的默认变基函数为Linear，Linear函数的参数有斜率和各向异性比率、角度三项。因此作者选用北西向150°测线，网格间距分别为50m×50m、70.7m×70.7m、86.6m×86.6m，斜率分别设为0.5、1、2(默认值为“1”)，各向异性比率1、2.5、5(默认为“1”)，各向异性角度为30°、0°、150°(默认值为0°)，在网格化后，计算插值数值与采样数值的绝对误差均方根值，计算结果如图3所示。

表1 不同变基函数的ΔT绝对误差均方根值

由图3可知，对于给定测线方向、网格间距时，不同斜率的ΔT绝对误差均方根值基本相同；各向异性角度在各向异性比率大于“1”时对网格化结果有影响，对于给定斜率，各向异性比率为5、角度为30°时的ΔT绝对误差均方根值小于其他参数的计算值，即各向异性角度与测线方向为正交时，计算得到的ΔT绝对误差均方根值较小；当侧线角度为45°、0°时，上述结论依然成立。

5 搜索范围的影响

克里金方法高级选项还有搜索范围参数，为此选用北西向150°测线，网格间距为50 m×50 m、70.7 m×70.7 m、86.6 m×86.6 m，变基函数为Linear，斜率为“1”(默认值)，各向异性比率5(默认值为“1”)，各向异性角度为30°(默认值为0°)，搜索椭圆的两个半径之比分别设为：1/1、1/2.5、1/5、2.5/1、5/1(默认值为1/1)，搜索角度设为30°、0°、150°(默认值为0°)，网格化后计算插值数值与采样数值的绝对误差均方根值。50 m×50 m、86.6 m×86.6 m计算结果如图4所示(70.7 m×70.7 m与86.6 m×86.6 m图形相似)。

由图4可以看出，搜索半径比率、搜索角度对网格化结果的影响较斜率和各向异性小；搜索半径比率对网格化结果的影响大于搜索角度的影响；搜索角度为150°的ΔT绝对误差均方根值小于30°、0°。当测线方向为45°、0°，网格间距为50 m×50 m、70.7 m×70.7 m、86.6 m×86.6 m时，可以得出相同规律。

图2 点块和漂移模式的ΔT绝对误差均方根值

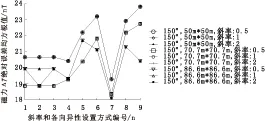
图3 斜率和各向异性的ΔT绝对误差均方根值

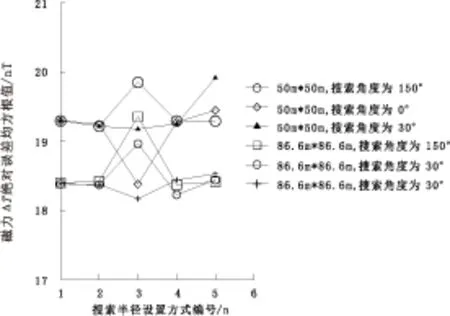
图4 不同搜索范围的ΔT绝对误差的均方根值

6 结论

1)克里金网格化方法中，不同的变基函数插值结果相差较大，产生的误差最大、最小之比可达10倍。

2)Linear和Power是十二种变基函数中ΔT绝对误差均方根值最小的变基函数，二者的插值结果基本相同，Power的计算时长稍大于Linear。

3)Point(点) 模式的误差大于Block(块)模式的误差。

4)Drift模式对网格化结果影响小于Kriging模式。

5)Linear变基函数的斜率对网格化影响很小，近乎为0 nT。

6)各向异性角度在各向异性比率大于“1”时对网格化结果有影响,当各向异性角度与测线方向为正交时，计算得到的ΔT绝对误差均方根值较小。

7)搜索半径比率、搜索角度对网格化结果的影响较斜率和各向异性小。

8)搜索半径比率对网格化结果的影响大于搜索角度的影响。

以上结论是基于Surfer8.0的Kriging网格化方法得出的，网格化过程是手工完成，测试的样本数据只考虑了测线方向为0°、45°、150°时，网格间距分别为50 m×50 m、70.7 m×70.7 m、86.6 m×86.6 m的情况，对于其他测线方向、其他网格间距，上述结论的适用性尚需进一步确认；网格化过程的手动环节对于取得高质量的样本数据有一定限制，疏漏之处难免，结论的正确性还需进一步验证。

[1] 陈欢欢，李星，丁文秀. Surfer8.0等值线绘制中的十二种插值方法[J].工程地球物理学报,2007,4(1):52-57. CHEN H H,LI X,DING W X.Twelve kinds of gridding methods of Surfer8.0 in isoline drawing[J]. Chinese Journal of Engineering Geophysics, 2007,4(1):52-57.(In Chinese)

[2] 刘兆平，杨进，武炜.地球物理数据网格化方法的选取[J].物探与化探,2010,34(1):93-97. LIU ZH P,YANG J,WU W.The choice of gridding methods for geophysical data[J]. Geophysical & Geochemical Exploration,2010,34(1):93-97.(In Chinese)

[3] 王兆国，程顺有，刘财.地球物理勘探中几种二维插值方法的误差分析[J].吉林大学学报：地球科学版,2013,43(6):1997-2004. WANG ZH G,CHENG SH Y,LIU C.Error analysis of several two-dimensional interpolation methods in the geophysical exploration[J].Journal of Jilin University:Earth Science Edition,2013,43(6):1997-2004. (In Chinese)

[4] 张颖，孟小红，刘国峰.基于克里金方法的地球物理数据规格化[J].石油天然气学报(江汉石油学院学报),2005,27(6):746-747. ZHANG Y,MENG X H,LIU G F.Gridding methods for geophysical data based on kriging method[J]. Journal Of Oil And Gas Technology(Journal Of Jianhan Petroleum Institute), 2005,27(6):746-747.(In Chinese)

[5] 曾怀恩，黄声享.基于Kriging方法的空间数据插值研究[J].测绘工程,2007,16(5):5-8. ZENG H EN,HUANG SH X.Research on spatial data interpolation based on Kriging interpolation[J]. Engineering of Surveying and Mapping,2007,16(5):5-8. (In Chinese)

[6] 郭志宏，管志宁，熊盛青.长方体ΔT场及其梯度场无解析奇点理论表达式[J].地球物理学报,2004,47(6):1131-1138.GUOZHH,GUANZHN,XIONGSHQ.CuboidΔTanditsgradientforwardtheoreticalexpressionswithoutanalyticoddpoints[J].ChineseJournalofGeophysics,2004,47(6):1131-1138.(InChinese)

[7] 李焓，邱之云，王万银.复杂形体重、磁异常正演问题综述[J].物探与化探,2008,32(1):36-43.LIH,QIUZHY,WANGWY.Areviewoftheforwardcalculationofgravityandmagneticanomaliescausedbyirregularmodels[J].Geophysical&GeochemicalExploration,2008,32(1):36-43.(InChinese)

The influence of parameter setting about gridded datagenerated by Kriging method

LI Zeng-tao1， GAO Peng2， ZHAN San-min1， ZHAN Xu2， YU Feng-dan2

(1. Geophysics and Geochemical Exploration Corporation,North-West bureau of Geologicalfor Non-Ferrous Metals,China， Xi’an 710068,China;2.Xi’an Institute of Geology and Mineral Resources, Xi’an 710054, China)

In order to study the role that the parameters of Kriging method play in the gridding, we grid the magnetic anomaly field of a cubic get by theorical formula using Kriging method. We reveal that magnetic anomaly field which the direction of survey line is 0°,45°,150°. Root mean square value of absolute error (RMSVAE) was calculated from gridded data and theoretical value. In this way, we can find out the best suit of gridding parameter which the RMSVAE is minimum. According to RMSVAE, it could conclude: variogram model play a crucial role in the RMSVAE of Kriging method; Linear and Power have the least RMSVAE of gridded data; spacing distance is a second factor which decide the range of RMSVAE; point，block Kriging mode and the ratio or angle of anisotropy cause larger RMSVAE when other parameters are the same；drift mode, the ratio on the radius of search ellipseand search angle have smaller RMSVAE, which we can ignore.

Kriging; gridding; absolute error; gridded parameter

2015-02-10改回日期：2015-04-10

中国地质调查局计划项目(1212011140094)

李增涛(1978-)，男，硕士，从事地球物理勘查工作，E-mail:lzt20050319@163.com。

1001-1749(2015)05-0666-05

P 628

A

10.3969/j.issn.1001-1749.2015.05.21