层状大地表面中心回线瞬变电磁响应特征

吴 琼， 李永博， 李 貅， 晋 达

(1.中国地质科学院 地球物理地球化学勘查研究所，廊坊 065000；2.长安大学 地质工程与测绘学院，西安 710054；3.中石化中原油田分公司 物探研究院，濮阳 457001)



层状大地表面中心回线瞬变电磁响应特征

吴 琼1， 李永博1， 李 貅2， 晋 达3

(1.中国地质科学院 地球物理地球化学勘查研究所，廊坊 065000；2.长安大学 地质工程与测绘学院，西安 710054；3.中石化中原油田分公司 物探研究院，濮阳 457001)

中心回线装置下水平地层的时间域电磁场表达式为双重积分，内层为汉克尔型积分，外层为正弦或余弦积分，线性数字滤波法是求解此类特殊积分的有效方法。这里采用线性数字滤波法分别计算了均匀半空间、两层和三层介质共七种地电断面的电磁响应，分析了不同类型响应曲线的形态特征，研究了中间层厚度变化和底层电阻率变化对时间域响应曲线形态的影响。通过对比与分析，得出了一些规律性的认识，对于瞬变电磁数据的处理解释具有一定的指导意义。

汉克尔积分变换； 正弦变换； 余弦变换； 线性数字滤波； 瞬变电磁响应

0 引 言

瞬变电磁法具有工作效率高、电性分辨力强、探测深度大、抗干扰能力强等显著优势,因而被广泛应用于矿产勘探、工程勘察、环境灾害地质调查等多个领域[1-4]。时间域瞬变电磁响应的求取通常有两种方案：①直接法，根据一定的初始条件和边界条件在时间域中直接求解；②间接法，即频-时转换，根据频谱分析理论，首先在频率域求解给定场源的电磁响应，再通过傅里叶反变换求得相应的时间域电磁响应[5]。因频率域电磁场表达式较为简单，故其应用更为普遍。

实现频-时转换的主要方法有离散傅里叶变换法、延迟谱法、逆拉普拉斯变换法、数字滤波法等[5]，离散傅里叶变换法因其所需的频率和核函数抽样次数多、计算量大、速度慢而极少被采用，延迟谱法的晚期响应不太稳定，逆拉普拉斯变换法的计算量大、计算速度较慢，数字滤波法相比前三种方法，在层状大地情况下具有计算精度高、速度快且晚期响应稳定的优点，是当前较常用的一种计算方法。

在线性数字滤波算法方面，诸多学者开展了系列的研究工作，D.Guptasarma[6]提出了一种用于计算时间域激电响应的线性数字滤波算法，并给出了21点滤波系数；Aderson[7]提出了滞后褶积快速滤波算法；王华军[8]通过快速汉克尔变换理论导出了正弦变换和余弦变换数字滤波算法，给出了两组250点滤波系数，并验证了这组滤波算法具有计算速度快、精度高的优点[9]。

这里采用250点正弦变换滤波算法，分别计算了一层(均匀半空间)、两层和三层水平介质的时间域电磁响应，总结了典型地电断面的电磁响应曲线特征，并研究了中间层厚度变化和底层电阻率变化对时间域响应曲线形态的影响，得到了一些规律性的认识。

1 理论基础

一个半径为a的圆形线圈水平放置在水平地层表面，通入电流的大小为I0，角频率为ω，磁导率为μ。水平地层的电导率由上到下依次为σ1、σ2、…、σn-1、σn，各地层厚度依次为H1、H2、…、Hn-1、∞。采用柱坐标系，设原点在圆回线中心点，取z轴向下为正。当z=0时，接收线圈位于地表，此时各电磁场分量在频率域的积分表达式为[1]：

(1)

(2)

(3)

当忽略位移电流，并在中心点接收时：

Eφ=Hr=0

(4)

(5)

公式(5)为各向同性水平地层表面圆回线源中心点的频率域电磁场表达式，在回线中心点只能观测到磁场的垂直分量。在均匀半空间这一特殊情况下，回线源中心点频率域垂直磁场的积分表达式可化简为式(6)。

(6)

谐变电流条件下的电磁场量Hz(ω)与阶跃电流条件下的电磁场量Hz(t)满足如下关系：

(7)

利用欧拉公式、Hz(ω)的复数性质、δ(ω)函数的积分性质、积分区间的对称性、ReHz(ω)和lmHz(ω)的奇偶性及其频率特性等[1]，可得：

(8)

其相应的时间导数为：

(9)

文中水平层状介质的时间域响应，采用250点正弦变换滤波算法,计算公式为[9-10]式(10)。

(10)

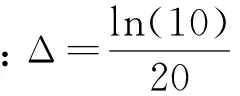
2 模型计算

2.1 均匀半空间

为研究时间域响应曲线随回线半径的变化规律，令I0=1A、ρ1=1 Ω·m，回线半径a分别取五个不同的值，求得的时间域响应曲线如图1所示。

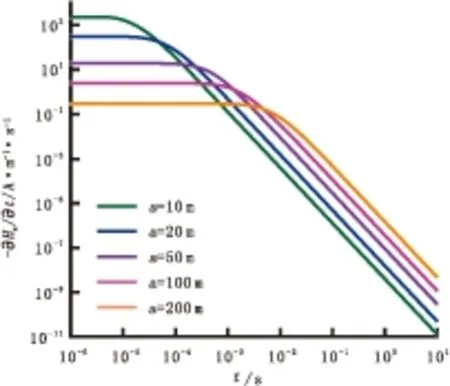
图1 均匀半空间时间域响应(不同回线半径)

为研究时间域响应曲线随电阻率的变化规律，令I0=1 A、a=100 m，均匀半空间电阻率ρ1分别取五个不同的值，求得的时间域响应曲线如图2所示。

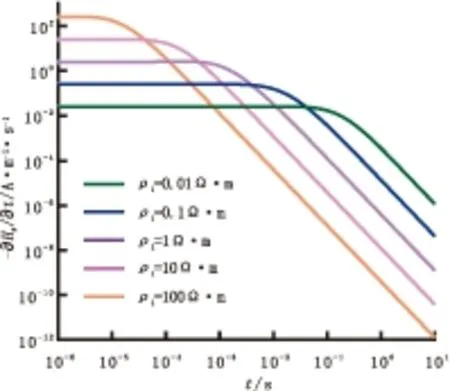
图2 均匀半空间时间域响应(不同电阻率)

均匀半空间时间域响应曲线具有如下规律性特征：在双对数坐标下，早期响应曲线近乎水平，晚期响应曲线为向下倾斜的直线，与时间轴的夹角约为68.2°。回线源半径越小，在中心点的早期响应幅值越大，越早进入晚期，均匀半空间电阻率越小，在中心点的早期响应幅值越小，越晚进入晚期。

2.2 两层模型

两层模型分为G型和D型两种地电断面，其参数取值如图3所示，线性数字滤波法求得的时间域响应见图4。

图3 两层模型示意图

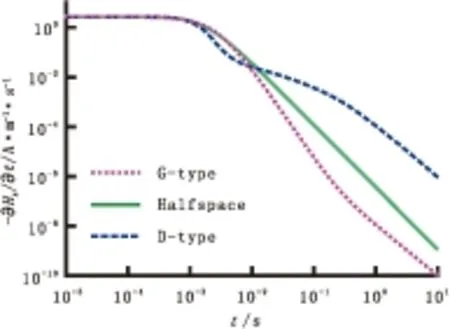
图4 两层模型时间域响应

从时间域响应曲线形态来看，三者在早期阶段基本重合，在双对数坐标下，为近水平的直线，随着时间的推移，G型逐渐向下偏离均匀半空间响应曲线，D型先向下后向上偏离均匀半空间响应曲线。由于瞬变电磁场服从热传导方程的规律，随着时间的增加，场向深处传播过程中以“烟圈”形式逐渐向外扩散，时间域响应逐渐衰减，而衰减曲线的斜率对应着地层的信息，G型的第二层电阻率大于第一层电阻率，故时间域响应衰减速率增大，表现为时间域响应曲线在均匀半空间响应曲线的下方，D型的第二层电阻率小于第一层电阻率，故时间域响应衰减速率减小，表现为时间域响应曲线在均匀半空间响应曲线的上方。响应曲线的两种不同形态，是由于层状模型高电阻率目标或低电阻率目标的电磁场衰减特性引起的。由此可见，瞬变电磁响应曲线反映了地下介质的电性变化特征，即当电磁场由低阻层进入高阻层时衰减加快，当电磁场由高阻层进入低阻层时衰减放慢。

2.3 三层模型

三层模型分为A型、K型、H型和Q型四种地电断面，其参数取值如图5所示。线性数字滤波法求得的时间域响应见图6。

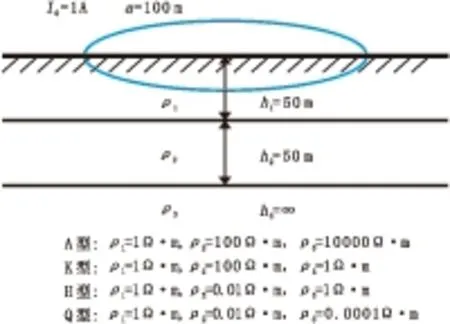
图5 三层模型示意图

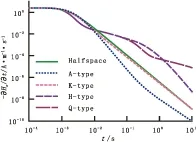
图6 三层模型时间域响应

从时间域响应曲线形态来看，五者形态各异。在双对数坐标下，随着时间的推移，A型逐渐向下偏离均匀半空间响应曲线，在中晚期衰减变快；K型和均匀半空间响应曲线首尾重合，在中期衰减稍快；H型围绕均匀半空间响应曲线先“下凹”后“上凸”，在晚期逐渐向均匀半空间响应曲线靠近；Q型呈“下凹”、“上凸”、“下凹”、“上凸”规律性变化，尤其在晚期，曲线衰减极为缓慢。总体来看，A型是GG型组合，H型是DG型组合，K型是GD型组合，Q型是DD型组合，因此在中晚期阶段，曲线的形态变化仍是与电磁场是由低阻进入高阻还是由高阻进入低阻两种不同电性界面性质有关。

2.4 改变中间层厚度模型

令G型、D型地电断面的第一层厚度与A型、H型、K型、Q型地电断面的第二层厚度分别取25m、50m、100m，同类型模型的其他参数取值保持固定，计算出的时间域响应曲线如图7所示。

由图7(a)、7(b)可见，G型、D型地电断面的时间域响应曲线在早期与均匀半空间响应曲线基本重合，随着时间的推移，G型曲线逐渐向下偏离均匀半空间响应曲线，D型曲线先向下后向上偏离均匀半空间响应曲线，G型和D型的第一层厚度越小，曲线偏离越明显，在晚期阶段，三种不同第一层厚度的G型和D型时间域响应曲线均具有重合趋势。由图7(c)、7(e)可见，A型、K型地电断面的时间域响应曲线在早期与具有相同地电参数的G型时间域响应曲线基本重合，随着时间的推移，A型曲线逐渐向下偏离G型响应曲线，K型曲线逐渐向上偏离G型响应曲线，不同第二层厚度的A型和K型时间域响应曲线均比较接近，很难分辨。由图7(d)、7(f)可见，H型、Q型地电断面的时间域响应曲线在早期与具有相同地电参数的D型时间域响应曲线基本重合，随着时间的推移，H型曲线逐渐向下偏离D型响应曲线，Q型曲线先向下后向上偏离D型响应曲线，H型和Q型的第二层厚度越小，曲线偏离越明显，在晚期阶段，三种不同第二层厚度的H型和Q型时间域响应曲线均具有重合趋势。

2.5 改变底层电阻率模型

令G型、D型、A型、K型、H型、Q型六种地电断面的底层电阻率分别取3个不同的值，同类型模型的其他参数取值保持固定，计算出的时间域响应曲线如图8所示。

由图8(a)可见，第二层电阻率越大，G型曲线向下偏离均匀半空间响应曲线越明显，但当第二层电阻率增大到一定程度后，其取值的不同在时间域响应曲线中难以辨别。由图8(b)可见，第二层电阻率越小，D型曲线先向下后向上偏离均匀半空间响应曲线幅度越大，在晚期阶段，第二层电阻率不同的三种D型时间域响应呈直线形态，且平行于均匀半空间情况下的晚期响应。由图8(c)可见，第三层电阻率不同的三种A型时间域响应曲线基本重合，无明显差异。由图8(d)可见，第三层电阻率越大，H型曲线向下偏离D型响应曲线越明显，但当第三层电阻率增大到一定程度后，其取值的不同在时间域响应曲线上反映得不再明显。由图8(e)可见，第三层电阻率越小，K型曲线偏离G型响应曲线越明显，在晚期阶段，第三层电阻率不同的三种K型时间域响应曲线几乎平行。由图8(f)可见，第三层电阻率越小，Q型曲线先向下后向上偏离D型响应曲线幅度越大，第三层电阻率不同的三种Q型时间域响应曲线差异明显，并在晚期阶段，呈相互平行的直线。

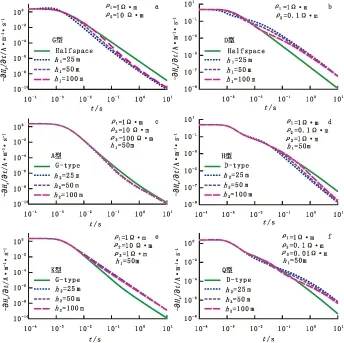
图7 改变中间层厚度模型时间域响应

图8 改变底层电阻率模型时间域响应

3 结 论

通过对均匀半空间、两层和三层介质共七种地电断面的电磁响应曲线进行对比分析，得到以下几点认识和结论：

1)在双对数坐标下，早期的时间域响应曲线为平行于时间轴的直线；晚期的时间域响应曲线为向下倾斜的直线，它与时间轴的夹角约为68.2°。

2)回线源半径越小，在中心点的早期响应幅值越大，越早进入晚期；地层电阻率越小，在中心点的早期响应幅值越小，越晚进入晚期。

3)当由低阻层进入高阻层(G型)时，电磁响应衰减加快；当由高阻层进入低阻层(D型)时，电磁响应衰减放慢。

4)A型与G型地电断面的电磁响应非常接近，不易分辨；K型和均匀半空间响应曲线首尾重合，在中期衰减稍快，反映了中间层的高阻特征；H型围绕均匀半空间响应曲线先“下凹”后“上凸”，在中期衰减较慢，反映了中间层的低阻特征；Q型呈“下凹”、“上凸”、“下凹”、“上凸”规律性变化，尤其在晚期，曲线衰减极为缓慢。时间域电磁法对高阻层的分辨能力远没有对低阻层的分辨能力强。

5)G型和D型地电断面的第一层厚度越小，电磁响应曲线偏离均匀半空间响应曲线越明显，在晚期阶段，不同第一层厚度的G型和D型时间域响应曲线均具有重合趋势；不同第二层厚度的A型和K型时间域响应曲线均比较接近，很难分辨；H型和Q型的第二层厚度越小，曲线偏离具有相同地电参数的D型时间域响应曲线越明显，在晚期阶段，不同第二层厚度的H型和Q型时间域响应曲线均具有重合趋势。

6)G型地电断面的第二层电阻率越大，其响应曲线向下偏离均匀半空间响应曲线越明显，但当第二层电阻率增大到一定程度后，其取值的不同在时间域响应曲线中难以辨别，在晚期阶段，第二层电阻率不同的G型时间域响应曲线具有重合趋势；D型地电断面的第二层电阻率越小，其响应曲线先向下后向上偏离均匀半空间响应曲线幅度越大，在晚期阶段，第二层电阻率不同的D型时间域响应呈直线形态，且平行于均匀半空间情况下的晚期响应。在中晚期阶段，A型和H型时间域响应曲线随第三层电阻率的变化规律与G型时间域响应曲线随第二层电阻率的变化规律类似，K型和Q型时间域响应曲线随第三层电阻率的变化规律与D型时间域响应曲线随第二层电阻率的变化规律类似。

上述规律性认识对于瞬变电磁资料的处理和解释，具有一定的参考价值。

[1] 方文藻，李予国，李貅. 瞬变电磁测深法原理[M]. 西安: 西北工业大学出版社，1993.FANGWZ,LIYG,LIX.Theprincipleoftransientelectromagneticsoundingmethod[M].Xi’an:NorthwesternPolytechnicUniversityPress, 1993. (InChinese)

[2] 朴化荣. 电磁测深原理[M]. 北京: 地质出版社，1990.PIAOHR.Principleofelectromagneticsoundings[M].Beijing:GeologicalPublishingHouse, 1990. (InChinese)

[3] 李貅. 瞬变电磁测深的理论与应用[M]. 西安: 陕西科学技术出版社，2002.LIX.Thetheoryandapplicationoftransientelectromagneticsounding[M].Xi’an:ShaanxiScienceandTechnologyPress, 2002. (InChinese)

[4] 牛之琏. 时间域电磁法原理[M]. 长沙: 中南大学出版社，2007.NIUZHL.Timedomainelectromagneticmethods[M].Changsha:CentralSouthUniversityPress, 2007. (InChinese)

[5] 陈向斌, 胡社荣, 张超. 瞬变电磁场响应计算的频-时域转换方法综述[J]. 工程地球物理学报, 2008, 5(2)：242-246.CHENXB,HUSR,ZHANGCH.Reviewoffrequency-domainandtime-domaintransformationmethodintransientelectromagneticfieldresponsecomputation[J].ChineseJournalofEngineeringGeophysics, 2008, 5(2): 242-246. (InChinese)

[6]GUPTASARMAD.Computationofthetime-domainresponseofapolarizableground[J].Geophysics, 1982, 47: 1574-1576.

[7]ANDERSONWL.FastHankeltransformsusingrelatedandlaggedconvolutions[J].Assn.Comp.Math.,Trans.,Math.Software, 1982, 8: 344-368.

[8]JOHANSENHK,SORENSENK.FastHankeltransforms[J].GeophysicalProspecting, 1979, 27: 876-901.

[9] 王华军. 正余弦变换的数值滤波算法[J]. 工程地球物理学报, 2004, 1(4): 329-335.WANGHJ.Digitalfilteralgorithmofthesineandcosinetransform[J].ChineseJournalofEngineeringGeophysics, 2004, 1(4): 329-335. (InChinese)

[10]吴琼. 大回线源电磁场正演与波场变换理论研究[D]. 西安: 长安大学，2012.WUQ.Forwardmodelingoflargelooptransientelectromagneticfieldandwave-fieldtransformtheory’sstudy[D].Xi’an:Chang’anUniversity, 2012. (InChinese)

Response features of central-loop transient electromagnetic field on the layered earth

WU Qiong1, LI Yong-bo1, LI Xiu2， JIN Da3

(1.Institute of Geophysical and Geochemical Exploration, Langfang 065000,China;2. School of Geology Engineering and Geomatics, Chang'an University, Xi'an 710054, China；3. Geophysical Research Institute, Zhongyuan Oilfield Company, SINOPEC, Puyang 457001, China)

The expressions of time-domain electromagnetic fields with a central-loop on the layered earth are double integrals. The inner integral is Hankel transform while the outer integral is sine transform or cosine transform. Linear digital filtering is an effective method to solve such special integrals. The electromagnetic responses for half space, two-layer and three-layer models have been calculated with linear digital filtering method, and the response curves for the seven types (half space, G, D, A, K, H and Q) have been analyzed, and time-domain responses of layered models with changing interlayer-thickness and underlayer-resistivity have been studied. By comparing and analyzing, some regular cognitions are drawn, which have certain guiding significance for transient electromagnetic data’s processing and interpretation.

Hankel integral transform; sine transform; cosine transform; linear digital filtering; transient electromagnetic response

2015-05-11改回日期：2015-06-08

中央级公益性科研院所基本科研业务费项目(AS2013P01)

吴琼(1986-)，女，硕士，主要从事电磁勘探理论与方法技术研究，E-mail：wuqiong8668@163.com。

1001-1749(2015)05-0560-06

P 631.3

A

10.3969/j.issn.1001-1749.2015.05.03