航空磁测中正常地磁场校正

骆 遥 ， 罗 锋， 王 明， 何 辉， 王林飞

(中国国土资源航空物探遥感中心，北京 100083)



航空磁测中正常地磁场校正

骆 遥 ， 罗 锋， 王 明， 何 辉， 王林飞

(中国国土资源航空物探遥感中心，北京 100083)

在地球物理勘探中，磁异常是地磁场同正常地磁场的差，去除正常地磁场背景能够获得磁异常信息，正常地磁场校正是航空磁测资料处理中的必要环节。这里从航空磁测资料处理实际出发，针对正常地磁场计算、校正中坐标系变换、改正方式等关键问题进行分析，同时对行业规范中存在的问题进行讨论，以明确航空磁测中正常地磁场校正处理的方式，这些结论可供地面磁法勘探参考。

正常地磁场； 国际地磁参考场； 航空磁测； 航磁资料处理； 磁法勘探

0 引言

中国航空磁测创始于1953年，航空磁测已基本覆盖我国陆域和大部分海域，部分区域实现了多次覆盖[1]。航空磁测在大地构造、地质填图、固体矿产与石油天然气勘查、城市稳定性评价、地质灾害预测及其他地学研究等方面得到广泛应用，其解决国家战略性、先导性问题的能力为人瞩目，社会各界对航空磁测资料的需求不断增多。区别于地面磁法勘探，航空磁测具有其自身的测量特色和一套完整的数据处理与解释方法，使用航磁成果资料中需要特别重视航空磁测数据采集与处理。正常场校正是获取ΔT异常的关键，作者从磁异常的概念出发，结合航空磁测测量实际情况讨论了航空磁测中正常场计算和校正方法，同时针对相关行业规范较系统地讨论了正常场计算、校正中的关键问题，这对理解航空磁测正常场校正以及应用航磁资料具有意义。

1 地球磁场

地磁场是由地球内部磁性岩石及分布于地球内部和外部的电流产生的多种磁场叠加而成，分为内源场和外源场。内源场包括起源于地核的主磁场(地核场)和起源于地壳的岩石圈磁场(地壳场)。外源场主要由分布在磁层、电离层以及行星际空间的电流体系引起，是空间电磁环境在地球上的直接表象。此外，外源场也会在地球内部生成感应电流产生感应磁场。从全球平均看，地核场占总磁场的95%以上，地壳磁场约占4%，外源变化磁场及其感应磁场只占总磁场的1%[2]。尽管主磁场不像外源场那样快速地剧烈变化，却仍长期不断变化，表现最为显著的是偶极矩的变化、磁极移动等现象[3]。地磁场在航海、航空航天、国防工业、基础科学研究中具有重要作用，世界上许多国家和地区每隔一定周期发布自己的主磁场模式或地磁图，国际地磁学和高空大气学协会(International Association of Geomagnetism and Aeronomy, IAGA)每五年发布一次国际地磁参考场(International Geomagnetic Reference Field, IGRF)[4]，中国从1950年起每十年发布一次中国地磁图或中国区域主磁场模式[5-6]。地球主磁场强度高达数万纳特，勘探中被探测目标的磁异常多为主磁场所掩盖，需要选取并去除正常地磁场背景，获得与地壳相关的磁异常信息，此外诸如位场转换等资料处理和解释中也要求使用ΔT异常，这是磁法勘探中正常地磁场校正的目的。由于能够分离内源场和外源场，全球性地磁场建模中一直采用1839年高斯应用于地磁场的球谐函数分析方法，这也是现代地磁学的数理基础。按照高斯理论，内源磁场的标量位满足拉普拉斯方程，解的球谐函数形式为式(1)：

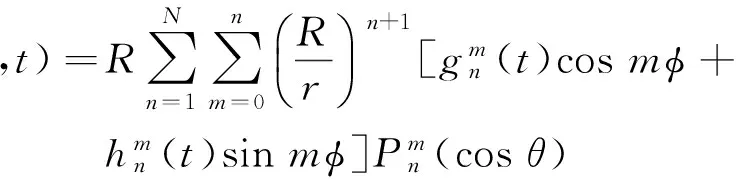
(1)

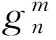
(2)

即

(3)

地磁场其他要素，总强度F、水平强度H、磁偏角D和磁倾角I，则可由地磁场矢量的三个分量X、Y、Z确定：

(4)

上述计算地磁场要素的表达不仅适用于主磁场建模，同样也适用于岩石圈磁场建模及综合建模，其区别主要在于球谐函数展开项与球谐系数的不同。当前通过航磁、船磁以及卫星磁测资料构建岩石圈磁场模型正逐渐成为热点[7]。

2 正常场校正问题

地磁场球谐分析理论是正常地磁场校正的基础，上述论述同教科书及相关技术规范大体相同，但现行教科书及相关技术规范却往往没有对正常地磁场计算与校正中几个重要的细节进行阐述，造成对资料处理的误解，作者将试图解决航空磁测正常地磁场计算与校正过程中遇到的各种“困惑”，这些对航空磁测的讨论同样适用于地面磁法测量或海洋磁测。

2.1 IGRF模型选择

同其他广泛开展航空物探的国家相类似，中国航空磁测的正常地磁场校正经历了几个阶段。早期航空磁测采用零线改正方式进行正常地磁场校正，中国科学院建立中国地磁场泰勒多项式模式后，采用过泰勒多项式进行正常地磁场校正，上世纪80年代开始采用国际地磁参考场(IGRF)进行正常地磁场校正。早期航空磁测采用模拟记录，其资料整理、修正和成图均为人工，正常场只能通过人工确定ΔT零线的方式进行校正。1956年-1988年间航空磁测导航定位为目视布标领航、照相定位阶段，不能精确给出飞行测量的航迹，不具备通过数学模式计算正常地磁场的条件。1966年-1990年间航空磁测导航定位采用双曲线、多卜勒、应答、赛里第斯等电子导航设备，航迹恢复相对变得简便、准确，为数学模式计算正常地磁场提供了必要条件，加之中国科学院已建立了中国地磁场泰勒多项式模式[8]，正常地磁场校正改用泰勒多项式。1987年中国国土资源航空物探遥感中心率先引进全球定位系统(GPS)进行航空磁测试生产，1988年正式用于塔里木盆地东部地区1∶200 000 航磁测量，1989年以后全面推广了GPS。GPS的广泛应用为航空物探中高精度导航定位、航迹的快速准确恢复提供了手段，航磁采样点处准确的空间坐标为以数学模式计算正常地磁场奠定了基础。1987年中国国土资源航空物探遥感中心引进基于IBM 4341计算机的航空物探数据处理系统，该系统包含计算IGRF的FORTRAN 77源程序，航空磁测中正常地磁场改正逐步采用IGRF模式，1995年原中国地质矿产部发布的《航空磁测技术规范》(DZ/T 0142-1994)正式将使用IGRF进行正常地磁场校正列入行业推荐标准[9]。零线改正的缺陷显而易见，手工改正仅能大致去除数万纳特的正常场背景，测线间改正量差异造成的测线水平差异严重。此外，改正后的模拟记录资料由于缺少原始正常场信息，无法恢复磁场原始面貌，在区域性航磁编图中只能通过用周围数字收录测区资料进行纠正，才能基本消除模拟记录测区正常场校正误差[1]。

用泰勒多项式进行正常场校正一定程度上避免了上述问题，但泰勒多项式模式本身并不完善，泰勒多项式拟合地磁场不具备物理意义，拟合的地磁场各分量并不自洽，不满足位场所满足的拉普拉斯方程，加之缺乏中国境外邻区的地磁测量资料，泰勒多项式拟合的中国地磁场在国界边境存在较严重的边界效应，不能同境外地磁场衔接。此外，泰勒多项式建立的磁场模式不包含高程变量，仅是平面位置的函数，无法计算高空正常地磁场。其他主磁场建立方式，如矩谐分析、球冠谐分析、样条拟合等也存在诸如边界效应或不满足拉普拉斯方程等缺陷[10]。球谐函数模式如IGRF建模中虽然仅采用极少数的中国地磁测量数据，不能很好地拟合中国地磁场，但由于球谐分析的独特优势以及近年来卫星磁测资料的广泛应用，尽管不是表述中国主磁场“最好”的模式，但球谐函数模式无疑是一种“最佳”的模式，这是广泛采用IGRF等球谐函数模式进行正常地磁场校正的原因。除IGRF外还有其他一些基于球谐函数的主磁场模型，如美国国防部、英国国防部、北大西洋公约组织等军事机构使用的标准地磁模型WMM[11]，尽管这类主磁场模型在细节上同IGRF略有不同，但正常的磁场计算和校正的讨论均适用于此类以球谐函数为数学背景的主磁场模型。

2.2 球谐函数阶次的选择

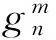
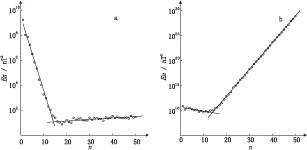
图1 地球磁场能谱

2.3 大地坐标系下主磁场计算

球谐分析理论是建立在球坐标系下的，式(1)-式(3)是建立在参考球体与球坐标系基础上的，公式中的经度、纬度并非通常意义下理解的经度、纬度，而需要进行坐标系变换，几乎所有教科书和规范都忽视了这点。GPS采用WGS-84坐标系，航空磁测作业中直接收录的是WGS-84坐标系下的经度、纬度和大地高，计算IGRF时需要将WGS-84大地坐标系转换至以地球为中心的球坐标系下，这也是IAGA推荐的。计算时取a2=40 680 631.6 km2，b2=40 408 296.0 km2，其中a、b分别是椭球体的长半轴和短半轴。设WGS-84下的经度为L、纬度为B，大地高为H，则

φ=L

(5)

θ′=90°-B

(6)

(7)

(8)

cosα=(H+RH)/r

(9)

sinα=cosθ′sinθ′(a2-b2)/r/RH

(10)

cosθ=cosα·cosθ′-sinα·sinθ

(11)

sinθ=cosα·sinθ′+sinα·cosθ′

(12)

通过式(5)-式(12)就可以得到式(3)计算所需的r、φ、cosθ、sinθ，式(3)中平均地球半径R取6 371.2 km。由式(3)计算得到的是地心坐标系下的主磁场要素，需要对纬向分量X′和垂直分量Z′旋转，将切于球面的X′和垂直球面的Z′旋转至切于椭球面的地磁场北向分量X和垂直椭球面的地磁场垂直分量Z，即

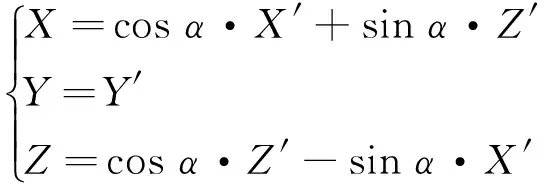
(13)

于是可将式(13)计算出的地磁场分量代入式(4)获取其他地磁要素。

2.4 高度校正或水平梯度校正问题

《航空磁测技术规范》(DZ/T 0142-2010)8.1.6.1中规定“地球正常磁场校正应按国际规定，使用有效的国际地磁参考场值”，而在8.1.6.3中又规定了“地球正常磁场垂向梯度校正，根据测量飞行的海拔高度差值，由国际地磁参考场计算校正”，即提出了正常地磁场的“高度校正”问题[13]。《地面磁法勘探技术规程》(SY/T 5771-2004)7.3.2中规定“正常场改正利用国际地磁参考场IGRF模型进行改正”，在7.3.3中规定了“高度改正值计算”，也提出了正常地磁场的“高度校正”问题[14]。《地面磁勘查技术规程》(DZ/T 0144-1994)则规定了“当测区沿地磁场梯度方向的正常磁场变化值等于或大于设计的总均方误差值时，对全部测点均须进行校正，校正应相对于总基点进行。所用正常梯度的数值和方向，应取自最近年代的国际地磁参考场”，又提出了正常地磁场“水平梯度校正”问题[15]。《地面高精度磁测技术规程》(DZ/T0071-1993)也规定了“正常梯度改正与高度改正”，要求“用国际地磁参考场提供的高斯系数，用电子计算机算出测区内1 km×1 km节点地磁场值，以1nT的间距绘制等值线图。用此图作正常场梯度改正”[16]。从事航空磁测及地面磁法勘探的技术人员不禁疑问，当前以IGRF作为校正正常地磁场的标准模式时，是否真存在“高度校正”和“水平梯度校正”的问题？

地球磁场是空间位置和时间的函数，地磁要素不仅存在时间变化率，在三维空间上也具有不同的变化率，即地磁场梯度。磁法勘探中现代磁力仪测量的是地磁场强度，正常地磁场校正就是用观测点测量的地磁场强度减去该测点IGRF计算出的主磁场强度，由于计算IGRF过程中需要代入该观测点处的坐标及高程，采用IGRF进行正常场校正事实上已经隐含解决了高度校正或水平梯度校正问题。出现正常地磁场的高度校正或水平梯度校正问题，是由于校正中考虑用基点处的正常地磁场值对全部观测点进行校正，这样主磁场的校正量为一个常量，还需要考虑观测点与基点空间位置差异，即水平位置差异及高程差异引起的主磁场强度变化。规范中涉及正常场高度校正或水平梯度校正时，其参考点同测量点正常地磁场的相对变化均是按IGRF(或IGRF的偶极子近似)计算而来，其改正精度必然与直接用IGRF校正各观测点处的正常地磁场等同(或偏低)，文献[17]给出了采用IGRF一阶近似校正误差分析的一个初步结果，认为当测点与基点沿纬度方向的距离大于9 km时，均方误差(水平梯度校正误差)将超出《地面高精度磁测技术规程》(DZ/T 0071-1993)要求，当测点与基点的高程差大于700 m时，计算的高度改正值均方误差(高度校正误差)将超出《地面高精度磁测技术规程》(DZ/T 0071-1993)的要求。目前磁测规范中水平梯度改正均采用IGRF，除了手工取值外不存在近似改正问题，与直接用观测点处的IGRF值(不考虑测点间或与基点间高程变化，即不考虑高度校正问题)改正无异，以下仅以正常地磁场垂直梯度为例进行讨论。如果仅考虑偶极子场，正常场垂直梯度可近似为：

(14)

仅与正常场强度F和地心距r相关。《地面高精度磁测技术规程》(DZ/T 0071-1993)、《航空磁测技术规范》(DZ/T 0142-1994)、《地面磁法勘探技术规程》(SY/T 5771-2004)均采用式(14)计算正常地磁场垂向梯度进行校正。

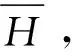
(15)

相应的正常场校正为

FΔH(L,B,H)

(16)

其中：ΔT表示经IGRF校正后的ΔT；T为实测航磁采样点(L,B,H)处的地磁场强度；F0为采样点处的正常场；FΔH为高度校正值。将式(15)高度校正值代入式(16)，得到式(17)。

ΔT=T(L,B,H)-F0(L,B,H)

(17)

即实际正常地磁场校正过程实质就是利用采样点处地磁场的测量值减去该采样点处的IGRF值。如果按照《航空磁测技术规范》(DZ/T0142-2010)进行正常地磁场校正，即用式(15)和式(16)进行校正，需要两次计算同一采样点上两种高度上的IGRF[13]，采用式(17)直接校正采样点处的正常地磁场，则只需计算一次IGRF，校正结果却完全一致。实际上式(17)的含义是直接获取观测点处的磁异常，正常地磁场校正中的高度校正在理论上不具备新的地球物理意义。航空磁测中导航定位系统收录的GPS数据可直接用于计算IGRF，目前航空磁测中正常场校正也是直接采用式(17)方式进行处理。地面磁测与航空磁测无异，也应采用观测点处的IGRF进行校正。对于《地面磁勘查技术规程》(DZ/T0144-1994)中涉及基点归算磁场水平问题[15]，由于磁法本身仍属相对测量，最终归算到何种水平仅相差直流分量，实际上与高度校正或水平梯度校正问题本身无关。

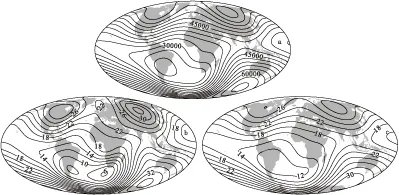
图2 地球正常地磁场强度及其垂直梯度

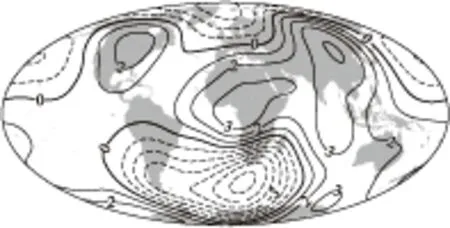
图3 两种地磁场总强度垂直梯度差异(等值线间隔1 nT/km)

2.5 其他问题

正常地磁场随时间长期变化，时间是IGRF模式中一个重要参量，包括《航空磁测技术规范》(DZ/T0142-2010)在内，各规范均没有对校正正常场至哪个时间点进行规定。采用IGRF原则上可以根据相隔五年的球谐系数或年变系数计算任意时间点的地磁要素，但实际IGRF的精度有限，通常只能按日计算。航磁测量飞行有着自身的特点，通常测量一个工区要持续数月或几年，理论上每架次测量数据的正常场校正均可改正至测量日当天的IGRF，但IGRF中采用的年变系数的精度有限，是对未来主磁场长期变化的预测，对每架次航磁数据进行逐日校正会带来不确定性，航磁资料通常只校正至工区开工之日。考虑到年变系数的预测因素，作者建议航磁测量中IGRF校正日期仅精确至年，例如2012年6月30日开工进行测量飞行的工区，其全部航磁数据校正的正常场均为2012年1月1日0时的IGRF。如果测量飞行的工区是跨年度飞行，分属不同年份采集的数据，作者也建议校正至开工年的IGRF，因为对一个工区的数据逐年或逐日、逐月的采用相应测量时间的IGRF进行校正会在连续的飞行测量的磁场曲面上人为引入由IGRF不同造成的测线水平误差，这是航空物探资料处理中所忌讳的。即使IGRF校正至开工年，也不会影响航磁资料的精度，因为航空磁测不是绝对测量而是相对测量，地球磁场是在不断变化的，尽管建立了各种地磁场模式力图消除地球磁场短期或者长期的变化，但其精度仍不能将磁异常视为绝对值。从另外一个角度讲，航磁测量不同的离地高度也进一步将测量值局限在相对值的范围内，因此所用航磁图件的磁场水平都是根据数据状况和解释者的需要随机确定的[18]。后续区域性航磁编图或编制全国航磁图时，也涉及正常场改正，需要根据DGRF对当时使用的IGRF进行重新修正，统一磁场水平，前期将IGRF校正至开工年份(部分航磁测量因测量年代“久远”，已经无法确切了解具体的开工日期，只能推算至开工年)也最有利于重新恢复原始资料处理中被校正的IGRF。

《航空磁测技术规范》(DZ/T0142-2010)中附录E规定“按给出的测区内控制点的经纬度(或测线某些点上实测经纬度值)，计算出具体的IGRF；根据计算出的测区内控制点处的IGRF，按测线内插出每个采样点处的IGRF”[13]，但规范中没有对“控制点”进行说明，“测线某些点”表述模糊。航空磁力仪的采样率可达每秒百次远超过GPS的采样率，例如中国国土资源航空物探遥感中心目前采用的HC-2000型航空氦光泵磁力仪的采样率为10次/s，GG-24双星座全球卫星导航定位仪的采样率为2次/s，也就是说除相邻2个GPS采样点处有磁场采样外，相邻2个GPS采样点间还存在4个磁场采样，非GPS采样点处的正常地磁场值需要内插得到。IGRF校正的明确表述应为，计算所有GPS采样点处的IGRF，根据测线上相邻GPS采样点的IGRF值内插出非GPS采样点处磁场采样的IGRF，并对磁场采样点数据进行校正。例如航磁作业飞行中Y-12飞机的航速约60m/s，GPS采样点的间隔约30m，磁场采样点的间隔为6m，而IGRF的空间分辨率约4 000km，内插的IGRF完全能满足高精度航空磁测的需要。此外，根据目前航空磁测作业情况，GPS的平面定位精度要优于高程的定位精度[19]，实际飞行测量中GPS实测高程有时存在抖动，在计算IGRF时需要对其进行检查、处理，以确保校正质量。

3 结论与建议

作者从航空磁测中正常地磁场校正处理的实际出发，讨论了正常地磁场计算、校正中的问题，这对深入理解航空磁测中的正常地磁场校正具有启示，对地面磁法勘探也具有借鉴性意义。从上世纪九十年代起，随着GPS的广泛应用与普及，磁法勘探中正常地磁场校正方法发生了深刻性的变革，甚至一些带导航功能的智能手机都可以给出当前空间位置的正常地磁场信息，以手工方式从地磁图上取数改正的方式早已成为历史。但行业规范制定相对滞后，没用充分利用当前全球地磁场建模的优势，无法彻底抛弃早期正常地磁场校正的思维。作者认为应当从磁异常的概念出发，将观测点的磁场观测值直接去掉该测点处的正常地磁场以获得磁异常，不宜再引入高度校正或水平梯度校正等概念。此外，直接校正观测点处IGRF也符合国际上磁法勘探资料处理通行的做法。目前，《找矿突破战略行动纲要(2011—2020年)》经国务院同意，已正式下发，纲要提出“加快推进重点成矿区带基础地质调查和综合研究工作，重点开展1∶50 000 航空磁法测量，开展1∶250 000 航空地球物理调查”、“围绕重点成矿区带，加大航磁异常查证力度”，作者建议以此为契机，尽快对已相对滞后的规范进行修订，使之满足磁法勘探的切实之需，更好发挥航空磁测在找矿突破战略行动中的战略性、先导性作用。

致谢

感谢中国国土资源航空物探遥感中心王乃东、薛典军、段树岭、周坚鑫、熊盛青、陈斌等航空磁测技术专家对作者的帮助。

[1] 中国国土资源航空物探遥感中心. 中国及毗邻海域航空磁力ΔT异常图(1:5000000)[M].北京：地质出版社, 2004.ChinaAeroGeophysicalSurveyandRemoteSensingCenterforLandandResources.AeromagneticanomalymapofChinaandadjacentseaareas1:5000000.Beijing:GeologicalPublishingHouse, 2004. (InChinese)

[2] 徐文耀. 地球电磁现象物理学[M]. 合肥: 中国科学技术大学出版社, 2009.XUWY.Physicsofelectromagneticphenomenaoftheearth.Hefei:UniversityofScienceandTechnologyChinaPress, 2009. (InChinese)

[3] 王亶文. 二十世纪的地球偶极子磁场[J]. 地球物理学报, 2005,48(1): 52-55.WANGTW.Thegeomagneticdipolefieldinthe20thcentury.ChineseJ.Geophys.2005, 48(1): 52-55. (InChinese)

[4]FINLAYCC,MAUSS,BEGGANCD.InternationalGeomagneticReferenceField:theeleventhgeneration[J].GeophysicalJournalInternational, 2010,183(3):1216-1230.

[5] 安振昌, 徐元芳, 王月华. 1950—1980年中国地区主磁场模型的建立及分析[J]. 地球物理学报, 1991, 34(5): 585-593.ANZHC,XUYF,WANGYH.DerivationandanalysisofthemaingeomagneticfieldmodelsinChinafor1950-1980.ChineseJ.Geophys., 1991, 34(5): 585-593. (InChinese)

[6] 徐文耀. 我国地磁观测研究的发展[J]. 地球物理学报, 1994,40(S): 217-230.XUWY.AdvancesongeomagneticstudiesinChina.ChineseJ.Geophys., 1994, 40(S): 217-230. (InChinese)

[7] 徐文耀, 白春华, 康国发.地壳磁异常的全球模型[J]. 地球物理学进展, 2008,23(3): 641-651.XUWY,BAICHH,KANGGF.GlobalmodelsoftheEarth'scrustmagneticanomalies.ChineseJ.Geophys., 2008, 23(3): 641-651. (InChinese)

[8] 夏国辉, 郑双良, 吴莉兰, 等.1980年代中国地磁正常场图及其数学模式[J].地球物理学报, 1988, 31(1): 82-89.XIAGH,CHENGSHL,WULL,etal.ThegeomagneticfieldchartofChinain1980andthemathematicalmodel.ChineseJ.Geophys., 1988, 31(1): 82-89.(InChinese)

[9]DZ/T0142-1994. 航空磁测技术规范[S]. 北京: 中国标准出版社, 1995.DZ/T0142-1994.Criterionofaeromagneticsurvey.Beijing:StandardsPressofChina, 1995. (InChinese)

[10]徐文耀, 区加明, 杜爱民. 地磁场全球建模和局域建模[J]. 地球物理学进展, 2011,26(2): 398-415.XUWY,OUJM,DUAIM.Geomagneticfieldmodellingfortheglobeandalimitedregion.ChineseJ.Geophys., 2011, 26(2): 398-415. (InChinese)

[11]MAUSS,MACMILLANS,MCLEANS,etal.TheUS/UKWorldMagneticModelfor2010-2015[R].NOAATechnicalReportNESDIS/NGDC, 2010．

[12]MAUSS,ROTHERM,STOLLEC,etal.ThirdgenerationofthePotsdamMagneticModeloftheEarth(POMME)[J].Geochem.Geophys.Geosyst., 2006,7,Q07008,doi:10.1029/2006GC001269.

[13]DZ/T0142-2010. 航空磁测技术规范[S]. 北京: 中国标准出版社, 2010.DZ/T0142-2010.Criterionofaeromagneticsurvey.Beijing:StandardsPressofChina, 2010. (InChinese)

[14]SY/T5771-2004. 地面磁法勘探技术规程[S]. 北京：石油工业出版社, 2004.SY/T5771-2004.Technicalspecificationforgroundmagneticexploration.Beijing:PetroleumIndustryPress, 2004. (InChinese)

[15]DZ/T0144-1994. 地面磁勘查技术规程[S]. 北京: 中国标准出版社, 1995.DZ/T0144-1994.Specificationforgroundmagneticsurvey.Beijing:StandardsPressofChina, 1995. (InChinese)

[16]DZ/T0071-1993. 地面高精度磁测技术规程[S]. 北京: 中国标准出版社, 1994.DZ/T0071-1993.Specificationforhigh-precisiongroundmagneticexploration.Beijing:StandardsPressofChina, 1994. (InChinese)

[17]简燕, 李文尧, 武中华. 高精度磁测正常场改正和高度改正精度[J]. 物探与化探，2011，35 (3): 368-370.JIANY,LIWY,WUZHH.Adiscussiononnormalfieldcorrectionandaltitudecorrectionofhigh-precisionmagnaticsurvey.Geophysical&GeochemicalExploration, 2011, 35 (3): 368-370. (InChinese)

[18]王乃东. 有关1:25万航磁系列图的几个问题[J]. 物探与化探, 2007, 31(5): 459-464.WANGND.Someproblemsconcerning1: 250000aeromagneticseriesmaps.Geophysical&GeochemicalExploration, 2007, 31(5): 459-464. (InChinese)

[19]熊盛青, 于长春, 眭素文,等. 中高山区高精度航磁方法技术[M]. 北京: 地质出版社, 2009.XIONGSHQ，YUCHCH,SHUISW,etal.High-precisionaero-magneticsurveyinmedium-heightmountainousareas.Beijing:GeologicalPublishingHouse, 2009. (InChinese)

Removing the earth’s main field in processing of airborne magnetic data

LUO Yao, LUO Feng, WANG Ming, HE Hui, WANG Lin-fei

(China Aero Geophysical Survey and Remote Sensing Center for Land and Resources, Beijing 100083, China)

We can get magnetic anomalies by removing the normal magnetic field background of the earth, the normal magnetic field correction is a crucial step in airborne magnetic data processing. Based on the principle and practice, we discussed how to calculate the international geomagnetic reference field (IGRF) and how to correct the IGRF in airborne magnetic data processing. The discussions for the misunderstanding in the criterion for aeromagnetic survey should also be noted in the ground magnetic exploration.

normal magnetic field； international geomagnetic reference field； aeromagnetic survey； airborne magnetic data processing； magnetic exploration

2014-10-21改回日期：2014-11-12

国家高技术研究发展计划(863 计划)(2013AA063901)；中国地质调查项目(1212011087010)

骆遥(1982-)，男，高级工程师，主要从事航空地球物理探测工作，E-mail:geophy@vip.qq.com。

1001-1749(2015)05-0552-08

P 631.2

A

10.3969/j.issn.1001-1749.2015.05.02