菲涅尔面积分的计算
张思卿, 张新好, 党宝军, 李九凌
(1北京理工大学信息与电子工程学院北京100191 2中国人民解放军94326部队济南250023)
引 言
Fresnel面积分是一个积分下限含有自变量的双重复指数积分,无法通过直接求解得到。多年来,国内外学者提出了许多近似计算方法[1~4],其中文献[1,4]利用线积分的渐近展开式,给出了Fresnel面积分的近似计算,但其计算过程相当复杂、繁琐,在对角度γ1、γ2分类的基础上,还需对η值进行分类、判断,不便于工程应用。本文对文献[2,3]给出的Fresnel面积分计算公式进行详细推导和分析,基于Jacobi-Anger恒等式和Bessel函数的性质,提出了一种新的Fresnel面积分近似计算公式,并与文献[3~5]的结果进行对比验证。
1 Fresnel面积分的类型
由文献[6]可知,双雷达栅多路径传播损耗模型中的八个场分量,均含有Fresnel面积分

式中,q1、q2、u0、m和n均为实常数。I下标的正负号与m的正负号相对应,其分类及计算公式见表1。
令

式中,hf1为第一个雷达栅的高度,hf2为第二个雷达栅的高度,hA为天线的高度,hT为目标的高度。
则

式中,λ为波长,d1、d2、d3分别为天线与第一个雷达栅、第一个雷达栅与第二个雷达栅、第二个雷达栅与目标间的距离。

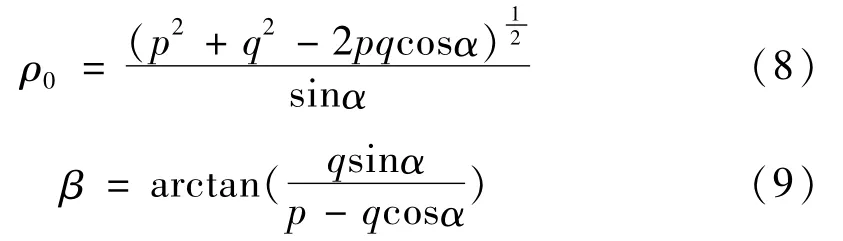
式(6)~(9)中,α、p、ρ0、q、β等参数的物理意义见图1。
当p≥0、q>0且式(1)中m前面的符号为负时,式(1)的积分区域如图1中的阴影部分S1、S2所示。图中,阴影部分的顶点为o′,oo′的长度为ρ0,γ1=β,γ2=π-αβ。oo′的延长线o′N将阴影区域分为两个部分S1、S2(其它条件下的积分区域图形见参考文献[1])。
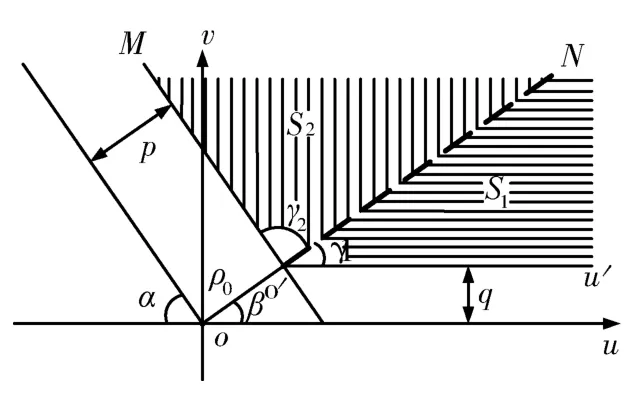
图1 Fresnel面积分I-的积分区域示意图(p≥0,q>0)Fig.1 Schematic diagram of integral domain of Fresnel surface integral I-

Table 1 Type of Fresnel surface integral表1 Fresnel面积分的类型[1]
2 G(ρ0,γ)的计算
Fresnel面积分的一般形式为

式(10)的积分区域见图2。
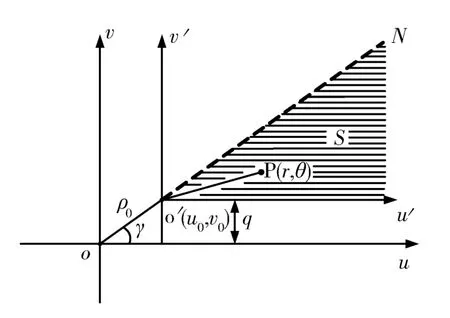
图2 Fresnel面积分的积分区域示意图Fig.2 Schematic diagram of integral domain of Fresnel surface integral
为便于计算,由

可得

将式(13)代入式(10),化简并令


由雅可比-安格尔(Jacobi-Anger)恒等式有[7]

代入式(14),得

因

有

由Bessel函数的性质[7]

可将式(18)分解为下列五项之和
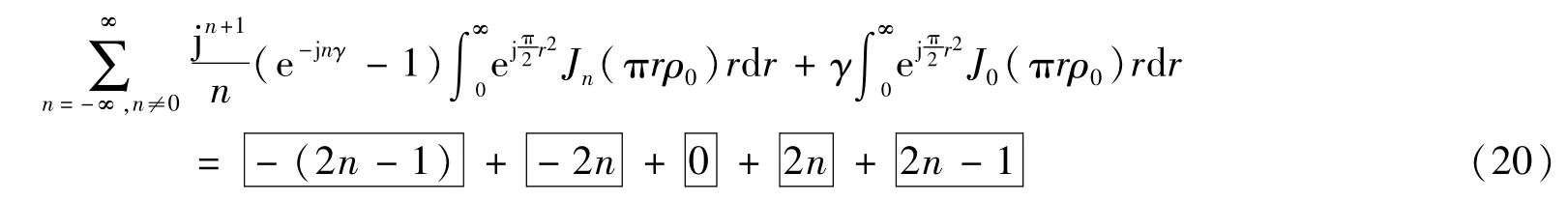
式中

利用Bessel函数积分的关系式[7]
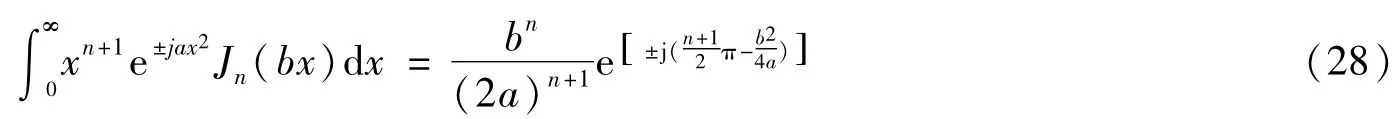
式中,a>0,b>0,1/2>Ren>-1(Re:实部)。

式中,a>0,b>0,Ren>-4。
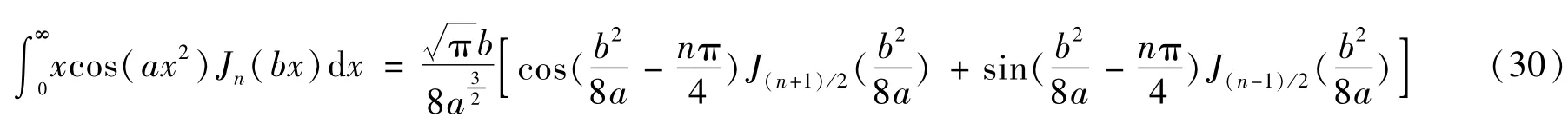
式中,a>0,b>0,Ren>-2。
将式(24)、式(27)中积分项化简为

将式(20)代入式(14),得

由式(21)、式(24)和式(27)可知

将上式代入式(33),得


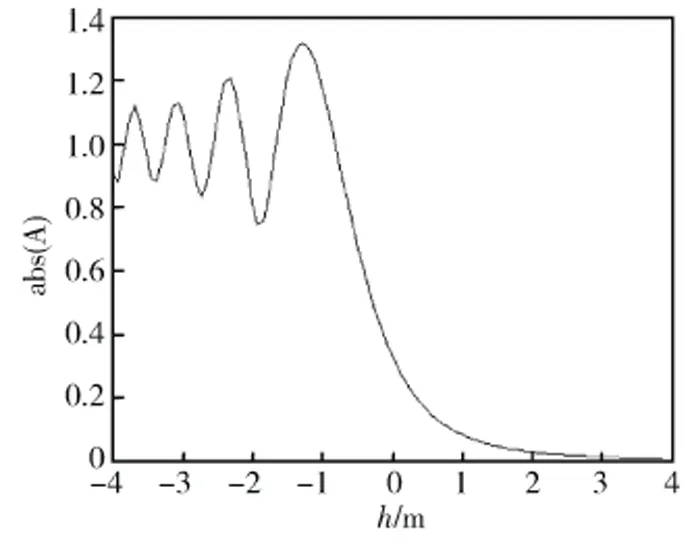
图3 由本文计算方法得到的文献[3]图1算例的计算结果Fig.3 Calculation results of Literature 3 Fig.1 by the proposed method in this paper(f=1GHz,d1=d2=d3=10m,h=h1=h2=-4m~4m,hA=hT)
此即为本文所得的Fresnel面积分近似计算公式。
3 算例验证
为验证本文近似计算公式的有效性,利用式(35)分别计算文献[3~5]给出的算例。图3为由式(35)得到的文献[3]图1算例的计算结果(注:图3中的纵坐标abs(A)为复衰减函数A的绝对值,A=E/EO,E为设置雷达栅时目标处的电场强度,EO为无雷达栅时目标处的电场强度,详见文献[3]),图4为由式(35)得到的文献[5]图4算例的计算结果,计算时式(35)中的n取1~100。表2给出了文献[4]第8节算例的计算结果对比。由图3、图4可以明显看出,利用本文的计算公式可得到与文献[3,5]完全一致的结论。从表2可以看出:当n取1~50时,其结果已满足计算精度要求。

图4 由本文计算方法得到的文献[5]图4算例的计算结果Fig.4 Calculation results of Literature 5 Fig.4 by the proposed method in this paper(VV-polarization,f=0.9GHz,d1=3000m,d2=2000m(Single Radar Fence,d2=5000m),d3=3000m,h f1=h A=100m,h f2=0,Γ1=Γ2=Γ3=1)

表2 与文献[4]计算结果的对比Table 2 Comparison of the calculation resultswith themethods in this paper and in Literature 4
4 结束语
本文针对传统Fresnel面积分计算方法存在的参数(γ1、γ2、η等)分类、判断多元,计算过程复杂、繁琐等问题,提出了一种新的近似计算方法。仿真结果表明:与传统计算方法相比,本文提出的近似计算方法物理意义清晰,计算方法简单,计算量小且收敛速度快,为Fresnel面积分的相关工程应用提供了便利。
[1]赵雄文.计及反射的刃峰、尖劈、平顶障碍绕射场的一致性解法[D].青岛:中国电波传播研究所硕士学位论文,1992.
[2]Schneider Michael, Luebbers R J.A General, Uniform Double Wedge Diffraction Coefficient[J].IEEE Transactions on Antennas and Propagation,1991,39(1):8~14.
[3]Savov SV, Andersen JB.Efficient Method for Calculation of Fresnel Double Integral[J].Electronics Letters, 1995, 31(6):435~437.
[4]Millington G, Hewitt R, Immirzi F S.The Fresnel Surface Integral[J].IEE Proceedings, 1962, 109C(162):430 ~437.
[5]Zhao Xiongwen, Vainkainen Pertti.Multipath Propagation Study Combining Terrain Diffraction and Reflection[J].IEEE Transactions on Antennas and Propagation,2001,49(8):1204~1209.
[6]张新好.0.8GHz-18GHz全频段外场散射及天线测量技术研究[D].北京:北京航空航天大学博士学位论文,2011:63~66.Zhang Xinhao.Study on the 0.8GHz-18GHz Outdoor RCS and Airborne Antenna Measurement System[D].Beijing University of Aeronautics and Astronautics,2011:63~66(in Chinese).
[7]《数学手册》编写组.数学手册[M].北京:高等教育出版社,1979:628.
[8]Gradshteyn IS, Ryzhik IM.Tables of Integrals, Series and Products[M].7th edition.New York:Academic Press, 2007:706,739.

