基于循环矩的高阶调制PCMA信号的参数估计*
曹玉健, 赵宇峰, 涂世龙, 戴旭初
(1中国科学院无线光电通信重点实验室中国科学技术大学信息科学技术学院 合肥 230026 2盲信号处理重点实验室 成都 610041)
引 言
通信信号的特征参数估计是非协作通信中很重要的研究课题,参数估计的准确与否对于后续的信号解调和分析有着至关重要的作用。成对载波多址(PCMA)是一种能够节省传输带宽的卫星通信信号多址方式[1]。对于单通道非协作接收到的PCMA信号来说,能否从时频混叠的信号中获得信号参数的准确估计是PCMA信号分离和解调的关键。
对于PCMA信号,需要估计的参数有符号率、频偏、载波相位、信号延时、信号功率等。目前,已有一些研究者从不同的角度,提出了一些PCMA信号或同频混合信号的参数估计方法。例如,文献[2]在假设其它参数已知和发送端的符号序列已知的情况下,对PCMA系统中的干扰信号幅度进行了估计;文献[3]利用PCMA信号包络的差分信息来估计信号的符号率;文献[4]则利用最大似然方法估计同频混合信号的时延;文献[5]研究了相位调制PCMA信号的谱线特征,并给出了时延的估计方法;文献[6]基于循环延迟自相关方法,提出了同频混合数字调制信号时延的闭式估计方法。总体而言,现有的关于PCMA参数估计的研究基本上都针对低阶调制的PCMA信号(如BPSK、QPSK等),而且其估计方法和算法都要求部分参数已知,且仅对个别的参数进行估计。而高阶调制PCMA信号(如8PSK、16QAM等)的参数估计,仍未得到深入研究。
本文首先介绍循环矩的定义及其性质,并分析高阶调制PCMA信号参数与二阶、四阶和八阶循环矩谱的关系。在此基础上,设计了高阶调制PCMA信号所有特征参数的估计方法,包括符号率、残留频偏、传输信道衰落系数、初始相位和定时误差估计。然后,根据本文提出的参数估计方法的特点,针对工程应用给出了循环矩的实用化估计方法。最后,通过仿真实验验证本文提出的高阶PCMA信号参数估计方法的有效性。
1 信号模型和问题描述
一个单通道接收机接收到下行PCMA信号,对其作放大、变频等处理后,基带信号y(t)可表示为

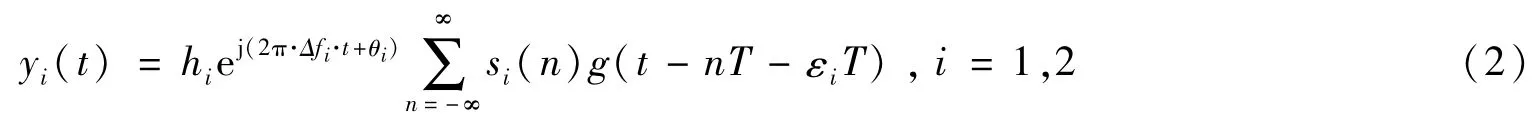
其中,T为发送符号的周期,si(n)为发送端传输的符号序列,且s1(n)、s2(n)具有相同的调制星座图,因本文考虑的是高阶调制,故为等效的传输衰落系数,通常在一个数据帧内,hi是恒定不变的;Δfi表示数字调制信号经过下变频后残留的频偏,θi为初始相位,εi为定时误差,且表示等效的基带成形滤波器,本文采用滚降系数为βi的升余弦滚降滤波器为零均值、功率为σ2v的平稳复高斯白噪声,且独立于s1(n)、s2(n)。
在式(1)和式(2)表示的PCMA信号模型中,残留频偏Δfi比较小,通常Δfi·T在10-5~10-2量级,且Δf1≠Δf2。另外,由于s1(n)、s2(n)的符号率相同、调制方式相同,因此y1(t)和y2(t)在时域上完全重叠,频域上也几乎完全重叠。但是,数字调制信号具有循环平稳特性,其循环频率(循环平稳周期)与Δfi和T有关。
本文要研究的问题是:基于上述信号模型和循环平稳理论,探讨只利用接收到的单通道混合信号y(t)来估计高阶调制PCMA信号参数的方法和实现算法,需要估计的参数包括T、Δfi、hi、θi、εi。
2 高阶调制PCMA信号的循环矩(谱)特性
2.1 循环平稳信号的时变矩和循环矩
循环平稳信号x(t)的k阶时变矩[7]定义如下

其中,(*)j表示是否对第j个因子取共轭,m表示k阶矩中取共轭的数目。它的傅里叶变换

称为x(t)在循环频率α的k阶循环矩,式中[*]t表示时间平均。通常,将k>2的循环矩称为高阶循环矩。
由时变矩和循环矩的定义,可以得到循环矩谱具有下列三个性质
性质1:如果x(t)是k阶平稳信号,则当α≠0时,有Mαx(k,m)=0;
性质2:如果x(t)是k阶循环平稳信号,时变矩是周期为T的周期函数,即k,m),p为任意整数,则有

性质3:在k和m给定的情况下,是循环频率α的函数,此时也称为循环矩谱。如果循环矩谱存在离散谱线,则x(t)一定是k阶循环平稳信号。
由于MQAM的循环矩(谱)具有类似的特性,后续分析将以16QAM和8PSK信号为例,具体研究这两类数字调制信号的循环矩特征。
2.2 16QAM数字调制信号的循环矩谱特征
16QAM数字调制信号可表达为

2.2.1 二阶时变矩mx(t,2,1)和二阶循环矩谱
根据式(3)的定义和式(6),可以得到x(t)的二阶时变矩mx(t,2,1)为

很明显,mx(t,2,1)是周期为T的周期函数,其傅里叶变换为

其中B2(f)是g2(t)的傅里叶变换,即B2(f)=G(f)*G(f),G(f)是滚降系数为β的升余弦滤波器g(t)的傅里叶变换,*表示线性卷积,δ(f)是冲激函数。

可见,16QAM数字调制信号具有二阶循环平稳性,其非零的循环频率为α=±1/T,且与Δf无关。
2.2.2 四阶时变矩mx(t,4,0)和四阶循环矩谱
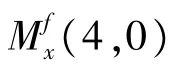
16QAM数字调制信号x(t)的四阶时变矩mx(t,4,0)为
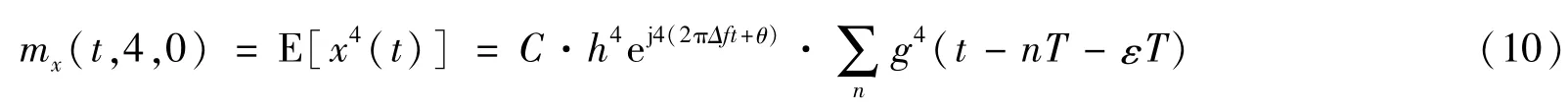
其中C是与调制星座图有关的常量,对于16QAM数字调制信号,C=-68。
由式(10)可知,mx(t,4,0)是周期函数,其周期为T。利用傅里叶变换性质,可得到其四阶循环矩谱为

式(11)中的B4(f)是g4(t)的傅里叶变换。
目前市面上流通较为广泛,价格比较大众化的正版英语输入材料,还是以阅读书籍为主,如外研出版社引进和出版的英语书虫系列书籍等。该系列由经典文学著作改编简化而成,为中英双语版本,纯文字,中高级难度,适合初、高中生阅读。对于更高水平的英语学习者,如英语专业的大学生,则有小众的高价英语原版小说,以及大学图书馆里的英语原版小说可供选择。

因此,16QAM数字调制信号具有四阶循环平稳性,其非零的循环频率为α=4Δf,4Δf±1/T,4Δf±2/T。由于B4(f)随着f增大而减小,所以有

2.3 8PSK数字调制信号的循环矩谱特征
8PSK数字调制信号可表示为

与16QAM数字调制信号类似,8PSK数字调制信号的二阶时变矩为
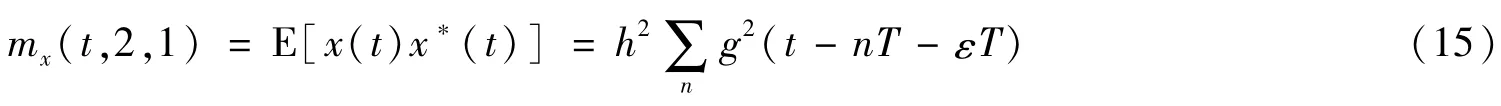
比较式(7)和式(15)可知,8PSK数字调制信号的二阶时变矩也是周期为T的周期函数,其二阶循环矩谱非零的循环频率为
根据时变矩的定义,易知8PSK数字调制信号的四阶时变矩均为0,但八阶时变矩不为零,有
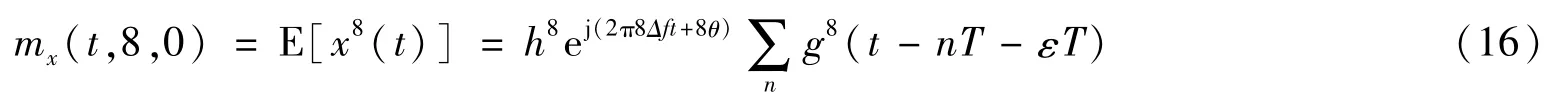
经过推导,其八阶循环矩谱为

其中B8(f)是g8(t)的傅里叶变换。由式(17)可知,8PSK数字调制信号具有八阶循环平稳性,由于B8(f)的带限特性和随着f增加的衰减特性,其非零的循环频率为通常取n≤2,且循环频率越大,其对应的谱线幅度越小,即

2.4 高阶调制PCMA信号的循环矩(谱)特征
对于式(1)和式(2)表示的PCMA信号,利用噪声v(t)的平稳性,以及s1(n)、s2(n)和v(t)之间的相互独立性,可以很容易得到下列结论。
①对于8PSK和16QAM PCMA信号,有

即对于PCMA信号,Mfy(2,1)只在处有离散谱线。
②对于16QAM PCMA信号,有
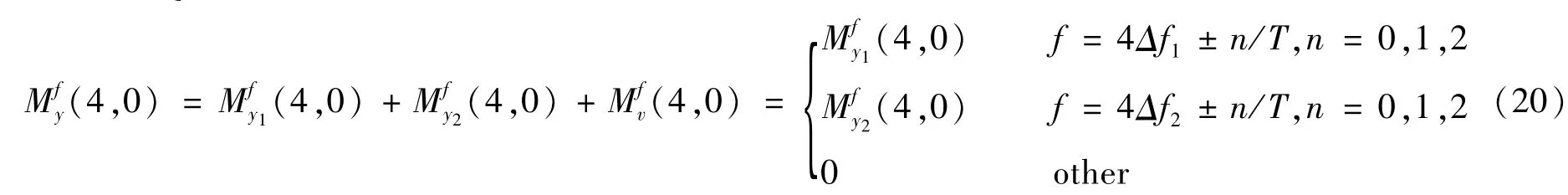
③对于8PSK PCMA信号,有

3 参数估计方法
根据第2节的分析可知,对于高阶调制PCMA信号,其二阶、四阶或八阶循环矩谱存在离散谱线,而谱线包含了PCMA信号中的特征参数信息,本小节将讨论利用循环矩谱中离散谱线的位置、幅度和相位信息来估计PCMA信号中两个分量信号参数的方法。
3.1 符号率和残留频偏的估计
PCMA信号的循环频率中含有符号率和残留频偏信息,因此只要通过循环矩谱确定离散谱线位置,即可获得循环频率,从而得到符号率和残留频偏的估计。
3.1.1 符号率的估计
由式(19)可知,不论是8PSK还是16QAM PCMA信号,其在0,处都有离散谱线,因此可将在f≠0处的最大值所对应的频率点作为符号率的估计,即

3.1.2 残留频偏的估计
①16QAM PCMA信号的残留频偏估计
其次,在集合Ω1中找到的最大值所对应的循环频率,便可获得一个残留频偏的估计,不失一般性,假设此时得到的是Δf1的估计,即

最后,去掉Ω1中与Δf1有关的元素,即4Δf1±n/T,得到子集Ω2:{4Δf2±n/T;n=0,1,2},进而获得Δf2的估计,即

②8PSK PCMA信号的残留频偏估计
对8PSK PCMA信号,由式(21)易知其八阶循环频率集合结合式(18)可知,8PSK八阶循环矩谱的离散谱线结构和特征与16QAM的四阶循环矩谱类似,故8PSK PCMA信号的残留频偏估计方法与16QAM的相同,即

3.2 传输衰落系数的估计
根据式(12)、(17)、(20)、(21),可得到循环矩与传输衰落系数hi的关系。对于16QAM PCMA信号,有

同理,对于8PSK PCMA信号,有

应该注意到,hi、B4(0)、B8(0)、C和T都是实数,因此,hi的估计为
对于16QAM PCMA信号

对于8PSK PCMA信号

由于滚降系数βi∈[1/3,1/2],且通过数值计算可知,B4(0)、B8(0)随不同βi值的变化不大,因此在实际应用中,取B4(0)≈0.64、B8(0)≈0.46即可。
3.3 初始相位和定时误差估计
初始相位θi和定时误差εi包含在离散谱线的相位信息中,根据式(12)、(17)、(20)、(21),并注意到B4(f)和B8(f)是实偶对称的,则可以利用循环矩谱中离散谱线的相位估计εi和θi。
对于16QAM PCMA信号


式中arg(z)表示对复数z求相角。
对于8PSK PCMA信号


3.4 循环矩谱的估计
由前文的讨论和分析可知,参数估计是通过y(t)的二阶、四阶或八阶循环矩谱来获得。在实际应用中,二阶、四阶或八阶循环矩谱是利用有限长的接收数据来估计的。
不失一般性,假设以采样频率fs对接收信号y(t)进行采样,得到接收信号的数据序列y(n)=y(t)|t=nTs,其中Ts=1/fs。为了防止频谱混叠,同时降低带外噪声的影响,通常选取fs≥Pfb,fb=1/T,P≥4。若用长度为N的数据y(n)来估计循环矩谱,则y(t)的二阶、四阶或八阶循环矩谱的估计为其中DFT[·]表示对序列进行离散傅里叶变换,通常用FFT算法来实现。

根据统计估计理论可知,循环矩谱的估计误差主要与数字信号的调制阶数、循环矩谱的阶数、信噪比、数据长度等诸多因素有关,在相同的估计误差条件下,调制阶数越高、循环矩谱的阶数越高、信噪比越低,所需要的数据长度越大。通过仿真实验,我们看到,为获得稳定可靠的估计,估计(2,1)、(4,0)和(8,0)所需要的数据长度分别不小于P·103、P·105和P·107,直接计算如此大长度的DFT,给实际的工程应用带来了很大的困难。下面根据本文参数估计方法的特点,给出有利于工程实现的循环矩(谱)的估计方法。
3.4.1 基于分段叠加的循环矩谱估计
符号率和残留频偏的估计只需要利用循环矩谱中离散谱线的位置信息,不要求幅度和相位的准确性,因此可考虑将长的数据序列分成若干段较短的序列,分段计算每段数据的时变矩。然后将分段数据的时变矩进行叠加平均后计算DFT,以获得离散谱线的位置。最后利用修正技术对离散谱线的位置进行修正,从而获得较为准确的循环频率估计。
不失一般性,假设将长度为N的数据分成K段,每段长度为Q,即N=KQ。以8阶循环矩谱的估计为例,令yk(q)=y8(q+kQ),q=0,…,Q-1,k=0,…,K-1,则8阶循环矩谱分段叠加估计为

当用FFT来计算式(39)时,由于FFT的长度为Q,故循环矩谱的频率分辨率为由于数据长度Q较短,FFT估计的频谱存在栅栏效应,离散谱线对应的频率值可能不等于理论上的循环频率。此时直接提取谱线位置来估计符号率和残留频偏存在误差,最大估计误差为因此有必要对直接估计结果进行修正,具体修正方法见文献[8]。该方法具有计算量小、修正效果明显的优点,受篇幅限制,这里不再赘述。仿真实验表明,采用修正技术后,循环频率的估计精度能够提高1~2个数量级。
3.4.2 基于递推计算的特定循环频率的循环矩估计
与符号率和残留频偏的估计不同,传输衰落系数、初始相位和定时误差的估计利用的是“特定循环频率点”上循环矩的幅度和相位信息。为了降低运算量,同时保证估计精度,可以采用随时间递推的方法估计特定循环频率的循环矩。

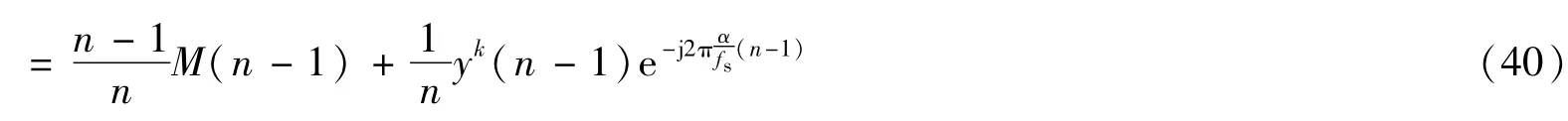
由此可得M(n)随时间递推的估计关系式
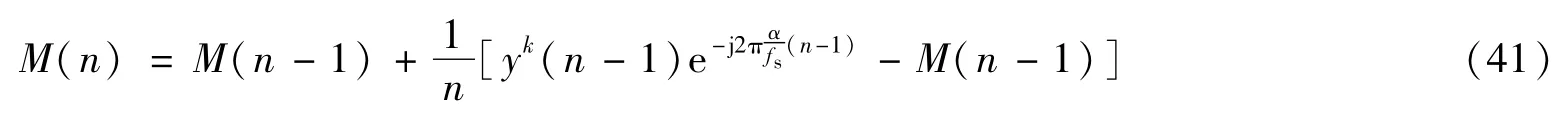
利用式(41)对特定循环频率的循环矩进行估计,由于在每个时刻的计算量非常小,因此该方法非常适合于工程应用。另外,随着n的不断增加,M(n)能够逐渐地逼近理论值。
4 仿真实验及分析
本小节将通过MATLAB仿真实验,验证本文提出的参数估计方法的有效性,并考察其性能特点。
仿真实验中,符号率、残留频偏、采样率都采用相对于符号率归一化的参数,即T=1,采样率fs=4,Δf1和Δf2分别在范围内随机选取。其它参数设置为初始相位θi随机选取;接收信噪比SNR定义为y1(t)和y2(t)的平均带内信噪比。另外,在估计二阶、四阶和八阶循环矩时,所用的符号数分别是107个,分段叠加法估计循环矩谱时,每个分段的长度是5×103个符号。所有的性能曲线都是通过对100次蒙特卡罗实验的结果进行平均获得的。
图1是PCMA信号符号率、残留频偏估计的相对误差与信噪比关系的仿真曲线,其中符号率估计的相对误差定义为为符号率的估计值;残留频偏估计的相对误差定义为两个残留频偏估计的相对误差的平均值,即和分别是两个残留频偏的估计值。从图1可以看出,当信噪比大于12dB时,不管是16QAM或者是8PSK PCMA信号,其符号率和残留频偏估计的相对误差都在10-7~10-6量级;但是当信噪比小于12dB时,8PSK PCMA信号的残留频偏估计性能随信噪比降低迅速恶化,这主要是因为八阶循环矩的估计对噪声比较敏感,而二阶和四阶循环矩的估计对噪声不敏感。
图2是PCMA信号传输衰落系数估计的相对误差与信噪比关系的仿真曲线,这里相对误差定义为由图2可知,当信噪比大于16dB时,16QAM PCMA信号和8PSK PCMA信号传输衰落系数的估计性能接近,相对误差大约在当信噪比小于14dB时,16QAM PCMA信号传输衰落系数的估计性能要优于8PSK PCMA信号,其原因也是八阶循环矩的估计对噪声比较敏感。

图1 符号率、残留频偏的估计性能与信噪比的关系Fig.1 The estimation performances of symbol-rate and frequency offsetwith SNR
图3和图4分别是PCMA信号初始相位和定时误差的估计性能与信噪比的关系曲线。可以看出,当信噪比大于16dB时,初始相位、定时误差估计的绝对误差都在10-3量级,而且16QAM和8PSK PCMA信号的估计性能非常接近,但是当信噪比小于14dB时,16QAM PCMA信号的估计性能要优于8PSK PCMA信号,与传输衰落系数估计性能的特点一致。

图2 传输衰落系数的估计性能与信噪比的关系Fig.2 The estimation performances of channel fading coefficientswith SNR
综合上述仿真结果,可以看出:①由于符号率和残留频偏估计只利用了离散谱线的位置信息,而传输衰落系数、初始相位和定时误差估计利用的是离散谱线的幅度或相位信息,因此符号率和残留频偏的可靠估计对信噪比的要求比其它参数的可靠估计大约低2~3dB;②在相同的信噪比条件下,8PSK PCMA信号参数估计的总体性能比16QAM PCMA信号略差;③高阶调制PCMA信号参数估计性能主要与使用的数据长度、信噪比、两个分量信号的功率差等因素密切相关,进一步的仿真实验表明,当两个信号的功率差大于3dB时,小功率信号参数的估计性能将明显下降,特别是对8PSK PCMA信号,受篇幅限制,这里不再展开讨论,将另文阐述。

图3 初始相位的估计性能与信噪比的关系Fig.3 The estimation performances of initial phases with SNR

图4 定时误差的估计性能与信噪比的关系Fig.4 The estimation performances of timing errors with SNR
5 结束语
本文以非协作接收PCMA信号为背景,以循环统计量为工具,对高阶调制PCMA信号的参数估计问题进行深入分析研究。通过对8PSK和16QAM PCMA信号循环矩的细致分析,获得了其二阶、四阶和八阶循环矩(谱)与信号诸多参数关系的解析表达式。在此基础上,针对高阶循环矩计算需要很长数据的问题,我们根据估计算法的特点,给出了高阶循环矩(谱)的实用化估计方法,即基于分段叠加的循环矩谱估计和基于递推计算的循环矩估计,为本文提出的参数估计算法的工程实现奠定了基础。仿真实验结果表明,利用高阶循环矩可以对高阶调制PCMA信号参数进行有效估计,且估计精度能够满足工程应用要求。
需要指出的是,本文给出的16QAM PCMA信号的参数估计方法同样适用于32QAM、64QAM等高阶QAM PCMA信号。另外,当8PSK PCMA信号中的两个分量信号的功率差大于3dB时,本文算法对较小功率分量信号的参数估计性能将明显下降,需要采用一些新的方法或措施改进本文算法,目前该项研究工作正在进展中。
[1]Dankberg M.Paired Carrier Multiple Access for Satellite Communication [C]//Pacific Telecommunications Conference,Hawaii, 1998, 1, 25 ~32.
[2]潘申富,白栋,依那,等.成对载波多址系统中干扰信号幅度的估计[J].真空电子技术,2003,21(02):21~24.Pan Shenfu, Bai Dong, Yi Na, et al.Estimation of Interference Amplitude in PCMA System[J].Vacuum Electronics,2003,21(2):21~24.
[3]郭 磊,任顺平,宣珠明.PCMA信号码元周期差分估计新方法[J].信息工程大学学报,2013,14(03):353~358.Guo Lei, Ren Shunping, Xuan Zhuming.New Method of Symbol Period Estimating in PCMA Signals[J].Journal of Information Engineering University,2013,14(03):353~358.
[4]廖灿辉,周世东,朱中梁.基于最大似然的同频混合信号联合定时估计算法[J].系统工程与电子技术,2010,32(06):1121~1124.Liao Canhui, Zhou Shidong, Zhu Zhongliang.ML-based Joint Timing Estimation Algorithm for Co-frequency Signals[J].Systems Engineering and Electronics,2010,32(06):1121~1124.
[5]郭一鸣,杨勇,张冬玲,等.单通道同频混合信号时延高效估计方法[J].系统工程与电子技术,2014,36(07):1416~1421.Guo Yiming, Yang Yong, Zhang Dongling, et al.Efficient Time Delay Estimation Algorithm for Single-channel Co-frequency Signals[J].Systems Engineering and Electronics, 2014, 36(07):1416 ~1421.
[6]赵宇峰,曹玉健,戴旭初.单信道混合数字通信信号的时延估计方法[J],信号处理,2015,31(2):161~169.Zhao Yufeng, Cao Yujian, Dai Xuchu.Time Delay Estimation for Single-channel Mixed Digital Communication Signals[J].Journal of Signal Processing, 2015, 31(2):161 ~169.
[7]张贤达,保铮.非平稳信号分析与处理[M].北京:国防工业出版社,1998.Zhang Xianda, Bao Zheng.Non Stationary Signal Analysis and Processing[M].Beijing:National Defense Industry Press,1998.
[8]Quinn BG.Estimation of Frequency, Amplitude, and Phase from the DFT of a Time Series[J].IEEE Transactions on Signal Processing, 1997, 45(3):814-817.

