基于CEI的高精度相位干涉测量试验*

任天鹏， 唐歌实， 刘景勇， 曹建峰，刘 禄， 陈 略，韩松涛，王 美

(1北京航天飞行控制中心北京100094 2航天飞行动力学技术重点实验室北京100094 3北京邮电大学北京100876)

引 言

目前，较为成熟的地球同步轨道(GEO)卫星轨道测定技术是单站RAE测量(R为距离，A为方位角，E为俯仰角)和多站nS/nR测量(S为距离和，R为距离)［1］。GEO卫星单站RAE测量中，受方位/俯仰测角精度限制，最终定轨精度为公里量级;多站nS/nR测量中，高精度距离测量需要利用航天器宽带转发器转发地面测站的测距信号，得到闭环的信号路径时延。无论是单站RAE测量，还是多站nS/nR测量，均为主动式测量，需要目标卫星合作转发测距信号。

干涉测量利用不同测站接收同一信号的相位差实现目标至测站间时延差的测量［2～4］。被动式干涉测量的技术优势有:①相对单站测角结果，干涉测量能够提供较高精度的测角信息;②干涉测量技术适用于不同调制信号，能够满足各类在轨卫星高精度轨道测量需求;③干涉测量技术仅接收下行信号，不占用星上宝贵的转发器资源。

目前，基于我国中科院的甚长基线干涉测量系统，干涉测量技术已经成功应用于我国“嫦娥”系列深空探测卫星的精密轨道测定任务［5～8］，而干涉测量技术在GEO卫星轨道测定领域的应用还处于探索阶段［9］。由于相位干涉测量对系统频率稳定度要求较高，因此通常仅适用于测站间频率同源的连线干涉测量CEI(Connected-Element Interferometry)系统［3，10］。本文推导了群时延辅助的相位干涉测量信号处理算法公式，利用北京航天飞行控制中心现已建成的基于光纤的连线干涉测量系统(基线长度约5.5km)开展了在轨GEO卫星干涉测量试验，完成了实测数据的相位干涉测量处理。通过对得到的干涉时延结果与GEO卫星精密星历得到的理论几何时延进行比较，验证了相位干涉测量精度能够满足GEO卫星高精度定轨要求。

1 群时延辅助的相位干涉测量

1.1 算法模型

干涉测量的观测量包括群时延与相时延:通过对单频段或多频段同源卫星信号进行宽带干涉处理，利用(带宽综合)干涉条纹斜率可提取群时延;利用干涉条纹相位或点频信号相位差可提取相时延。通过干涉处理解算出残余群/相时延值，将其叠加至时延模型值，即可得到干涉时延;利用标校技术得到群时延系统性误差τerror(钟差、设备和传播介质时延等)，则对干涉时延作τerror修正后得到的几何时延τ(t)可以应用于卫星轨道确定。

由于干涉带宽较窄造成干涉时延模糊范围大，因此干涉测量需要辅助一定精度的预报星历，才能使群时延解算结果无整周模糊度。令目标干涉测量群时延为τgroup(t)，则几何时延为τ(t)=τgroup(t)-τerror。

相时延指的是干涉相位与频率的比值。令相位干涉测量中相位测量值为则

其中，fsat为相位测量值对应的频点，τphase为干涉相时延，N为初始整周模糊度。将相时延系统性误差τp，error从干涉相时延中剔除，则几何时延可以表示为

需要说明的是，相时延系统性误差τp，error包括站间下变频随机初相误差，难以采用标校技术获取。

群时延与相时延均为体现目标至干涉测站的几何时延，存在1由于折射差异，电离层对群时延和相时延影响相反。长时间跟踪仰角变化的深空探测器等目标时，本式不能直接成立，需利用GPS技术等补偿仰角变化带来的电离层延迟变化［10］。跟踪GEO卫星时，电离层延迟为固定值，可以归为系统性误差，本式成立。

因此可以得到

为抑制观测噪声(尤其是群时延观测噪声)的影响，对一个弧段内观测结果取平均，得到相时延模糊值

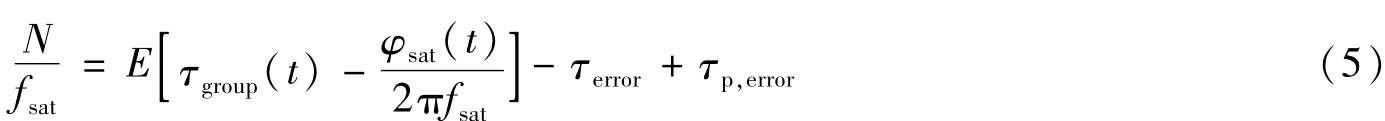
其中E［·］为均值估计。于是，基于相位干涉测量的卫星几何时延为

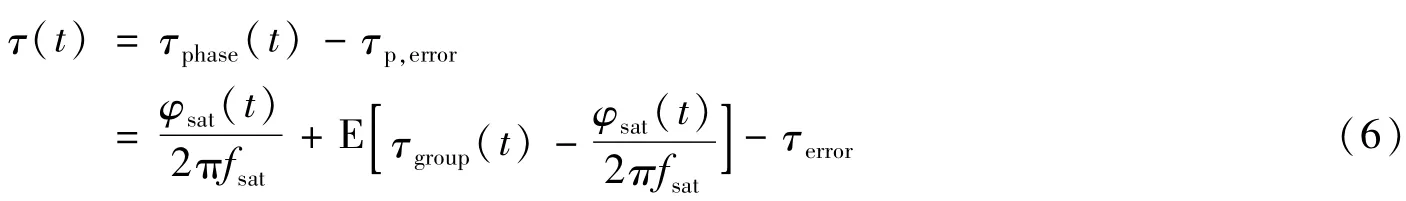
其中，群时延系统性误差τerror通常通过对标校源实测群时延与理论几何时延进行差分标校得到。当观测目标为单一卫星时，τerror可以采用实测群时延τgroup(t)与精密星历得到的理论几何时延τeph(t)之差，即

1.2 实测数据处理

由于GEO卫星在机动、漂星等期间仍有下行遥测信号，因此选择遥测信号为干涉测量对象。观测目标是北京时间2013年9月13日22:50至15日06:50的某广播卫星A，信号频谱如图1(a)所示。选择带宽约97kHz的遥测信号(如图1中圆圈标示)进行宽带干涉处理，9月13日22:50时信号干涉条纹如图1(b)所示(时延模型值为1.326×10-5s)。干涉群时延结果如图2(a)所示。由于干涉带宽较窄，群时延随机误差较大，约为7.24ns(RMS)。对采集到的卫星信号进行相位干涉处理，获取相时延，如图2(b)所示。显然，相时延随机误差较低，约为9.01ps(RMS)。结合已知的群时延，相位干涉测量得到的卫星A几何时延如图2(c)所示，图中群时延是每10个结果显示一次。

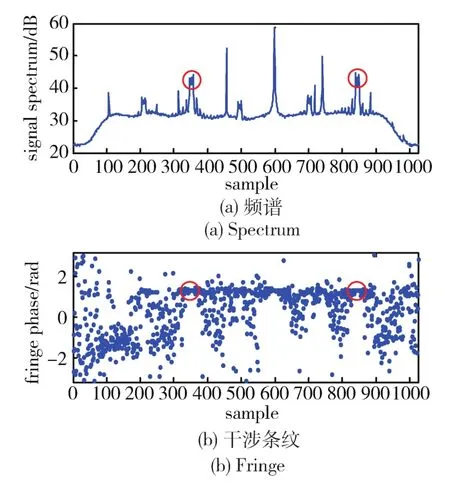
图1 卫星A下行信号频谱与干涉条纹(采样率f s=200kHz)Fig.1 Down-link signal spectrum and fringe of satellite A(sampling rate f s=200kHz)

图2 卫星A下行信号的干涉群时延、含模糊相时延和无模糊相时延Fig.2 Group delay，phase delay with ambiguity and phase delay without ambiguity of down-link signal of satellite A

2 实测干涉时延与理论几何时延比较

观测目标是北京时间2013年3月1日16:07至4日16:12的某广播卫星B。

利用连线干涉测量系统采集该卫星遥测信号，将信噪比较高的频带作为干涉对象，干涉带宽约198kHz。对采集到的卫星信号进行宽带干涉处理，获得群时延，如图3所示。群时延基本能够反映卫星轨道变化。然而，由于干涉带宽较窄，群时延随机噪声较大。较大的随机噪声将在卫星轨道解算中严重影响定轨算法的收敛速度和精度。将群时延与精密星历2该精密星历由多站nS轨道测定获得。本文利用该精密星历计算得到的几何时延作为理论几何时延，对实测干涉时延进行符合验证。得到的理论几何时延作对比，得到其精度约为2.30ns(RMS)，这是随机噪声和缓变系统误差共同作用的结果。

对采集到的卫星信号进行相位干涉处理，获得相时延。对相时延进行局部多项式拟合，拟合残差即随机误差约为7.49ps(RMS)。将相时延与精密星历得到的理论几何时延作对比，可以得到其精度约为0.118ns(RMS)，如图4所示，这主要是由缓变系统误差引起的。由图4左上方局部放大图亦可得此结论。

图3 群时延与理论几何时延的比较Fig.3 Comparison of group delay and theoretical delay

图4 相时延与理论几何时延的比较Fig.4 Comparison of phase delay and theoretical delay

由于0.118ns远小于2.30ns，因此群时延与精密星历得到的理论几何时延的差异中缓变系统误差贡献较小，可以认为随机噪声导致的群时延误差约为2.30ns(RMS)。换言之，相时延随机噪声较群时延随机噪声降低了两个数量级。

3 结束语

本文首先给出了群时延辅助的相位干涉测量信号处理算法，然后利用连线干涉测量系统对在轨GEO卫星下行信号做干涉测量试验和相位干涉处理，并将相时延与精密星历得到的理论几何时延进行对比。结果显示，相位干涉测量可以获得皮秒量级的相时延随机误差，远远优于纳秒量级的群时延随机误差;相时延与精密星历得到的理论几何时延差异约为0.1ns量级。利用5.5km的干涉基线，相位干涉测量角度误差不超过0.003°，与单站RAE测量相比，具有明显的测角精度优势。

本文工作得到了上海天文台张秀忠老师，国家授时中心杨旭海老师、陈亮老师，中国卫通公司杨学猛老师的指导和帮助，在此表示衷心的感谢。

［1］夏南银，等.航天测控系统［M］.北京:国防工业出版社，2002.Xia Nanyin， et al.Spaceflight TT&C Systems［M］.Beijing:National Defense Industry Press， 2002.

［2］程惠珍.基于地基CEI技术的空间飞行器相对位置测量技术研究［J］.飞行器测控学报，2008，27(4):33～36.Cheng Huizhen.Research on Relative Position Measurement of Spacecraft by Ground-based CEI［J］.Journal of Spacecraft TT&C Technology，2008，27(4):33～36.

［3］陈明，刘庆会，唐歌实，等.连线干涉系统测量共位双星宽带信号处理与分析［J］.中国科学院上海天文台年刊，2011，32(1):168～178.Chen Ming， Liu Qinghui， Tang Geshi， et al.The Wide Band Signal Process and Analysis of the Co-location Geostationary Satellite in Connected-Element Interferometry System［J］.Annals Shanghai Astronomical Observatory Chinese Academy of Sciences，2011，32(1):168～178.

［4］杜 兰，李晓杰，王若璞.基于同波束CEI的GEO共位卫星相对轨道监视［J］.大地测量与地球动力学，2012，32(3):50～54.Du Lan，Li Xiaojie and Wang Ruopu.Relative Orbit Monitoring of GEO Co-located Geostationary Satellites by Using Same Beam CEI［J］.Journal of Geodesy and Geodynamics， 2012， 32(3):50 ～54.

［5］曹建峰，黄勇，胡小工，等.USB与VLBI联合确定“嫦娥一号”卫星撞月点的位置［J］.宇航学报，2010，31(7):1724～1729.Cao Jianfeng， Huang Yong， Hu Xiaogong， et al.Determination of Impact Site of CE-1 Using USB and VLBIData［J］.Journal of Astronautics，2010，31(7):1724～1729.

［6］陈 明，张宇，曹建峰，等.嫦娥二号卫星轨道确定与测轨技术［J］.科学通报，2012，57(9):689～696.Chen Ming， Zhang Yu， Cao Jianfeng， et al.Orbit Determination and Tracking Technology of CE-2 Satellite［J］.Chinese Science Bulletin，2012，57(9):689～696.

［7］陈冠磊，郑鑫，陈明，等.基于卫星DOR信号的VLBI相时延解算方法研究［J］.天文学进展，2012，30(4):518～526.Chen Guanlei， Zheng Xin， Chen Ming， et al.Method of Calculating VLBIPhase Delay Based on DOR Signal of a Satellite［J］.Progress In Astronomy， 2012， 30(4):518 ～526.

［8］陈少伍，董光亮，李海涛，等.同波束干涉测量差分相时延观测模型研究及验证［J］.宇航学报，2013，34(6):788～794.Chen Shaowu， Dong Guangliang， LiHaitao， etal.Research and Verification of Differential Phase Delay Measurement Model of Same Beam Interferometry［J］.Journal of Astronautics， 2013， 34(6):788 ～794.

［9］杜 兰，郑 勇，李 杰.VLBI在GEO卫星精密定轨中的应用［J］.测绘科学技术学报，2006，23(4):269～271.Du Lan， Zheng Yong， Li Jie.VLBI-augmented Orbit Determination for Geostationary Satellites［J］.Journal of Zhengzhou Institute of Surveying and Mapping，2006，23(4):269～271.

［10］吴亚军，刘庆会，陈冠磊，等.VLBI相时延及其在深空探测器测定轨中的应用［J］.中国科学:信息科学，2014，44(2):221～230.Wu Yajun， Liu Qinghui， Chen Guanlei， et al.VLBIPhase Delay and Its Application in Orbit Determination of Spacecraft［J］.Scientia Sinica Informationis， 2014， 44(2):221 ～230.